自由能原理

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
Moonscar（讨论 | 贡献）2020年5月7日 (四) 20:01的版本 （Moved page from wikipedia:en:Free energy principle (history)）
(差异) ←上一版本 | 最后版本 (差异) | 下一版本→ (差异)
跳到导航 跳到搜索

此词条暂由彩云小译翻译，未经人工整理和审校，带来阅读不便，请见谅。

The free energy principle tries to explain how biological systems remain in non-equilibrium steady-states by restricting themselves to a limited number of states.[1] It says that biological systems minimise a free energy function of their internal states, which entail beliefs about hidden states in their environment. The implicit minimisation of free energy is formally related to variational Bayesian methods and was originally introduced by Karl Friston as an explanation for embodied perception in neuroscience,[2] where it is also known as active inference.

The free energy principle tries to explain how biological systems remain in non-equilibrium steady-states by restricting themselves to a limited number of states. It says that biological systems minimise a free energy function of their internal states, which entail beliefs about hidden states in their environment. The implicit minimisation of free energy is formally related to variational Bayesian methods and was originally introduced by Karl Friston as an explanation for embodied perception in neuroscience, where it is also known as active inference.

自由能原理试图通过将生物系统限制在有限的几个状态来解释生物系统是如何保持在非平衡稳态的。它说，生物系统最小化其内部状态的自由能功能，这包含了对其环境中隐藏状态的信念。自由能的内隐最小化在形式上与变分贝叶斯方法有关，最初由 Karl Friston 引入，作为神经科学中对具身知觉的解释，在那里它也被称为主动推理。


The free energy principle is that systems—those that are defined by their enclosure in a Markov blanket—try to minimize the difference between their model of the world and their sense and associated perception. This difference can be described as "surprise" and is minimized by continuous correction of the world model of the system. As such, the principle is based on the Bayesian idea of the brain as an “inference engine”. Friston added a second route to minimization: action. By actively changing the world into the expected state, systems can also minimize the free energy of the system. Friston assumes this to be the principle of all biological reaction.[3] Friston also believes his principle applies to mental disorders as well as to artificial intelligence. AI implementations based on the active inference principle have shown advantages over other methods.[3]

The free energy principle is that systems—those that are defined by their enclosure in a Markov blanket—try to minimize the difference between their model of the world and their sense and associated perception. This difference can be described as "surprise" and is minimized by continuous correction of the world model of the system. As such, the principle is based on the Bayesian idea of the brain as an “inference engine”. Friston added a second route to minimization: action. By actively changing the world into the expected state, systems can also minimize the free energy of the system. Friston assumes this to be the principle of all biological reaction. Friston also believes his principle applies to mental disorders as well as to artificial intelligence. AI implementations based on the active inference principle have shown advantages over other methods.

自由能原理是指那些系统---- 那些由马尔可夫覆盖层中的圈子所定义的系统---- 尽量减少它们的世界模型与它们的感觉和相关知觉之间的差异。这种差异可以被描述为”出其不意” ，并通过不断修正系统的世界模型来减少这种差异。因此，这个原理是基于贝叶斯的观点，即大脑是一个“推理机”。弗里斯顿为最小化增加了第二条路线: 行动。通过积极地将世界改变为预期的状态，系统还可以使系统的自由能最小化。弗里斯顿认为这是所有生物反应的原理。弗里斯顿还认为，他的原则适用于精神障碍和人工智能。基于主动推理原则的人工智能实现比其他方法显示了优势。


The free energy principle has been criticized for being very difficult to understand, even for experts.[4] Discussions of the principle have also been criticized as invoking metaphysical assumptions far removed from a testable scientific prediction, making the principle unfalsifiable.[5] In a 2018 interview, Friston acknowledged that the free energy principle is not properly falsifiable: "the free energy principle is what it is — a principle. Like Hamilton’s Principle of Stationary Action, it cannot be falsified. It cannot be disproven. In fact, there’s not much you can do with it, unless you ask whether measurable systems conform to the principle."[6]

The free energy principle has been criticized for being very difficult to understand, even for experts. Discussions of the principle have also been criticized as invoking metaphysical assumptions far removed from a testable scientific prediction, making the principle unfalsifiable. In a 2018 interview, Friston acknowledged that the free energy principle is not properly falsifiable: "the free energy principle is what it is — a principle. Like Hamilton’s Principle of Stationary Action, it cannot be falsified. It cannot be disproven. In fact, there’s not much you can do with it, unless you ask whether measurable systems conform to the principle."

自由能原理被批评为难以理解，即使是专家也难以理解。关于这一原则的讨论也受到批评，认为它引用的形而上学假设与可检验的科学预测相去甚远，使这一原则不可证伪。在2018年的一次采访中，弗里斯顿承认，自由能原理不能被恰当地证伪: “自由能原理就是它的本来面目ーー一个原理。就像汉密尔顿的静止作用原理一样，它是不能被证伪的。这是不能被推翻的。事实上，除非你问可衡量的系统是否符合这一原则，否则你用它做不了什么。”


Background

The notion that self-organising biological systems – like a cell or brain – can be understood as minimising variational free energy is based upon Helmholtz’s work on unconscious inference[7] and subsequent treatments in psychology[8] and machine learning.[9] Variational free energy is a function of observations and a probability density over their hidden causes. This variational density is defined in relation to a probabilistic model that generates predicted observations from hypothesized causes. In this setting, free energy provides an approximation to Bayesian model evidence.[10] Its minimisation can therefore be used as an approximation to Bayesian inference. When a system actively makes observations to minimise free energy, it implicitly performs active inference and maximises the evidence for its model of the world.

The notion that self-organising biological systems – like a cell or brain – can be understood as minimising variational free energy is based upon Helmholtz’s work on unconscious inference and subsequent treatments in psychology and machine learning. Variational free energy is a function of observations and a probability density over their hidden causes. This variational density is defined in relation to a probabilistic model that generates predicted observations from hypothesized causes. In this setting, free energy provides an approximation to Bayesian model evidence. Its minimisation can therefore be used as an approximation to Bayesian inference. When a system actively makes observations to minimise free energy, it implicitly performs active inference and maximises the evidence for its model of the world.

自我组织的生物系统——比如细胞或大脑——可以被理解为最小化变分自由能的概念，是基于亥姆霍兹在无意识推理以及随后的心理学和机器学习治疗方面的工作。变分自由能是观测值及其隐含原因的概率密度的函数。这个变分密度的定义关系到一个概率模型，生成预测观测从假设的原因。在这种情况下，自由能提供了一个近似贝叶斯模型的证据。因此，它的最小化可以用来近似于贝叶斯推断。当一个系统积极地进行观测以最小化自由能时，它隐含地进行积极推理并最大化其世界模型的证据。


However, free energy is also an upper bound on the self-information of outcomes, where the long-term average of surprise is entropy. This means that if a system acts to minimise free energy, it will implicitly place an upper bound on the entropy of the outcomes – or sensory states – it samples.[11][12]模板:Better source

However, free energy is also an upper bound on the self-information of outcomes, where the long-term average of surprise is entropy. This means that if a system acts to minimise free energy, it will implicitly place an upper bound on the entropy of the outcomes – or sensory states – it samples.

然而，自由能也是结果自信息的一个上限，长期的平均值是熵。这意味着，如果一个系统采取行动来最小化自由能，它将隐含地放置一个熵的结果-或感官状态-它的样本上限。


Relationship to other theories

Active inference is closely related to the good regulator theorem[13] and related accounts of self-organisation,[14][15] such as self-assembly, pattern formation, autopoiesis[16] and practopoiesis引用错误：没有找到与</ref>对应的<ref>标签. It addresses the themes considered in cybernetics, synergetics[17] and embodied cognition. Because free energy can be expressed as the expected energy of observations under the variational density minus its entropy, it is also related to the maximum entropy principle.[18] Finally, because the time average of energy is action, the principle of minimum variational free energy is a principle of least action.

</ref>. It addresses the themes considered in cybernetics, synergetics and embodied cognition. Because free energy can be expressed as the expected energy of observations under the variational density minus its entropy, it is also related to the maximum entropy principle. Finally, because the time average of energy is action, the principle of minimum variational free energy is a principle of least action.

/ 参考。它涉及控制论、协同学和具身认知理论中所考虑的主题。由于自由能可以用变分密度下观测值的期望能量减去其熵来表示，因此它也与最大熵原理有关。最后，由于能量的时间平均值是作用量，因此最小变分自由能原理是最小作用量原理。


Definition

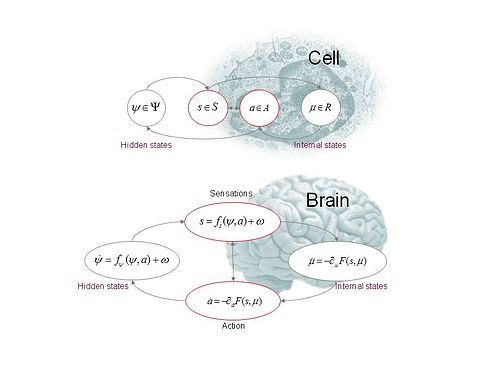
These schematics illustrate the partition of states into internal and hidden or external states that are separated by a Markov blanket – comprising sensory and active states. The lower panel shows this partition as it would be applied to action and perception in the brain; where active and internal states minimise a free energy functional of sensory states. The ensuing self-organisation of internal states then correspond perception, while action couples brain states back to external states. The upper panel shows exactly the same dependencies but rearranged so that the internal states are associated with the intracellular states of a cell, while the sensory states become the surface states of the cell membrane overlying active states (e.g., the actin filaments of the cytoskeleton).

These schematics illustrate the partition of states into internal and hidden or external states that are separated by a Markov blanket – comprising sensory and active states. The lower panel shows this partition as it would be applied to action and perception in the brain; where active and internal states minimise a free energy functional of sensory states. The ensuing self-organisation of internal states then correspond perception, while action couples brain states back to external states. The upper panel shows exactly the same dependencies but rearranged so that the internal states are associated with the intracellular states of a cell, while the sensory states become the surface states of the cell membrane overlying active states (e.g., the actin filaments of the cytoskeleton).

这些图表说明了状态划分为内部和隐藏或外部状态，这些状态被马尔可夫综合性分离，包括感觉和活跃状态。下面的面板显示了这个分区，因为它将应用于大脑的行动和感知; 在那里活跃和内部状态最小化感官状态的自由能功能。随后内部状态的自我组织然后对应感知，而行动夫妇的大脑状态回到外部状态。上面的面板显示完全相同的依赖性，但重新排列，使内部状态与细胞内的状态相关，而感官状态成为细胞膜上覆盖的活跃状态(例如，细胞骨架的肌动蛋白丝)的表面状态。


Definition (continuous formulation): Active inference rests on the tuple [math]\displaystyle{ (\Omega,\Psi,S,A,R,q,p) }[/math],

Definition (continuous formulation): Active inference rests on the tuple [math]\displaystyle{ (\Omega,\Psi,S,A,R,q,p) }[/math],

定义(连续公式) : 主动推理依赖于元组数学( Omega， Psi，s，a，r，q，p) / math,

  • A sample space [math]\displaystyle{ \Omega }[/math] – from which random fluctuations [math]\displaystyle{ \omega \in \Omega }[/math] are drawn
  • Hidden or external states [math]\displaystyle{ \Psi:\Psi\times A \times \Omega \to \mathbb{R} }[/math] – that cause sensory states and depend on action
  • Sensory states [math]\displaystyle{ S:\Psi \times A \times \Omega \to \mathbb{R} }[/math] – a probabilistic mapping from action and hidden states
  • Action [math]\displaystyle{ A:S\times R \to \mathbb{R} }[/math] – that depends on sensory and internal states
  • Internal states [math]\displaystyle{ R:R\times S \to \mathbb{R} }[/math] – that cause action and depend on sensory states
  • Generative density [math]\displaystyle{ p(s, \psi \mid m) }[/math] – over sensory and hidden states under a generative model [math]\displaystyle{ m }[/math]
  • Variational density [math]\displaystyle{ q(\psi \mid \mu) }[/math] – over hidden states [math]\displaystyle{ \psi \in \Psi }[/math] that is parameterised by internal states [math]\displaystyle{ \mu \in R }[/math]


Action and perception

The objective is to maximise model evidence [math]\displaystyle{ p(s\mid m) }[/math] or minimise surprise [math]\displaystyle{ -\log p(s\mid m) }[/math]. This generally involves an intractable marginalisation over hidden states, so surprise is replaced with an upper variational free energy bound.[9] However, this means that internal states must also minimise free energy, because free energy is a function of sensory and internal states:

The objective is to maximise model evidence [math]\displaystyle{ p(s\mid m) }[/math] or minimise surprise [math]\displaystyle{ -\log p(s\mid m) }[/math]. This generally involves an intractable marginalisation over hidden states, so surprise is replaced with an upper variational free energy bound. However, this means that internal states must also minimise free energy, because free energy is a function of sensory and internal states:

其目的是最大限度地提高模型证据的数学 p (s mid m) / 数学，或者最小限度地减少惊人的数学 -log p (s mid m) / 数学。这通常涉及隐状态的棘手边缘化，因此用变分自由能上界代替惊奇。然而，这意味着内部状态也必须最小化自由能，因为自由能是感官和内部状态的函数:


[math]\displaystyle{ a(t) = \underset{a}{\operatorname{arg\,min}} \{ F(s(t),\mu(t)) \} }[/math]
[math]\displaystyle{   a(t) = \underset{a}{\operatorname{arg\,min}}   \{ F(s(t),\mu(t)) \} }[/math]

Math a (t) underset { a }{ operatorname { arg ，min }{ f (s (t) ， mu (t))} / math

[math]\displaystyle{ \mu(t) = \underset{\mu}{\operatorname{arg\,min}} \{ F(s(t),\mu)) \} }[/math]
[math]\displaystyle{ \mu(t) = \underset{\mu}{\operatorname{arg\,min}} \{ F(s(t),\mu)) \}   }[/math]

Math mu (t) underset { arg ，min }{ f (s (t) ，mu) math


[math]\displaystyle{ \underset{\mathrm{free-energy}} {\underbrace{F(s,\mu)}} = \underset{\mathrm{energy}} {\underbrace{ E_q[-\log p(s,\psi \mid m)]}} - \underset{\mathrm{entropy}} {\underbrace{ H[q(\psi \mid \mu)]}} \lt math\gt \underset{\mathrm{free-energy}} {\underbrace{F(s,\mu)}} = \underset{\mathrm{energy}} {\underbrace{ E_q[-\log p(s,\psi \mid m)]}} - \underset{\mathrm{entropy}} {\underbrace{ H[q(\psi \mid \mu)]}} 数学下集{自由能}{底括号{ f (s，mu)}{底括号{ eq [-logp (s，psi mid m)]}{底括号{ h [ q (psi (mid mu)]}}} = \underset{\mathrm{surprise}} {\underbrace{ -\log p(s \mid m)}} + \underset{\mathrm{divergence}} {\underbrace{ D_{\mathrm{KL}}[q(\psi \mid \mu) \parallel p(\psi \mid s,m)]}} = \underset{\mathrm{surprise}} {\underbrace{ -\log p(s \mid m)}} + \underset{\mathrm{divergence}} {\underbrace{ D_{\mathrm{KL}}[q(\psi \mid \mu) \parallel p(\psi \mid s,m)]}} 下集-对数 p (s 中 m) + 下集下集 d (s 中 m)[ q (psi 中 μ)并行 p (psi 中 m)]} \geq \underset{\mathrm{surprise}} {\underbrace{ -\log p(s \mid m)}} }[/math]
 \geq \underset{\mathrm{surprise}} {\underbrace{ -\log p(s \mid m)}} </math>

在下列的数学中- log p (s mid m)} / math


This induces a dual minimisation with respect to action and internal states that correspond to action and perception respectively.

This induces a dual minimisation with respect to action and internal states that correspond to action and perception respectively.

这导致了对行为和内在状态的双重最小化，这两种状态分别对应于行为和感知。


Free energy minimisation

Free energy minimisation and self-organisation

Free energy minimisation has been proposed as a hallmark of self-organising systems when cast as random dynamical systems.[19] This formulation rests on a Markov blanket (comprising action and sensory states) that separates internal and external states. If internal states and action minimise free energy, then they place an upper bound on the entropy of sensory states

Free energy minimisation has been proposed as a hallmark of self-organising systems when cast as random dynamical systems. This formulation rests on a Markov blanket (comprising action and sensory states) that separates internal and external states. If internal states and action minimise free energy, then they place an upper bound on the entropy of sensory states

自由能最小化已被提出作为自组织系统的标志时，铸造为随机动态系统。这个公式建立在一个马尔可夫毯子(包括行动和感官状态) ，分离内部和外部状态。如果内部状态和作用力使自由能最小化，那么它们就在感觉状态的熵上设置了一个上限


[math]\displaystyle{ \lim_{T\to\infty} \frac{1}{T} \underset{\text{free-action}} {\underbrace{\int_0^T F(s(t),\mu (t))\,dt}} \ge \lt math\gt \lim_{T\to\infty} \frac{1}{T} \underset{\text{free-action}} {\underbrace{\int_0^T F(s(t),\mu (t))\,dt}} \ge 在下集{ text { free-action }{ underbrace { int 0 ^ t f (s (t) ，mu (t)) ，dt } \lim_{T\to\infty} \frac{1}{T} \int_0^T \underset{\text{surprise}}{\underbrace{-\log p(s(t)\mid m)}} \, dt = H[p(s\mid m)] }[/math]

\lim_{T\to\infty} \frac{1}{T} \int_0^T \underset{\text{surprise}}{\underbrace{-\log p(s(t)\mid m)}} \, dt = H[p(s\mid m)] </math>

林泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰泰


This is because – under ergodic assumptions – the long-term average of surprise is entropy. This bound resists a natural tendency to disorder – of the sort associated with the second law of thermodynamics and the fluctuation theorem.

This is because – under ergodic assumptions – the long-term average of surprise is entropy. This bound resists a natural tendency to disorder – of the sort associated with the second law of thermodynamics and the fluctuation theorem.

这是因为——在遍历性假设下——长期惊奇的平均值是熵。这种束缚阻止了一种自然的无序倾向，这种倾向与热力学第二定律和涨落定理有关。


Free energy minimisation and Bayesian inference

All Bayesian inference can be cast in terms of free energy minimisation; e.g.,.[20]模板:Failed verification When free energy is minimised with respect to internal states, the Kullback–Leibler divergence between the variational and posterior density over hidden states is minimised. This corresponds to approximate Bayesian inference – when the form of the variational density is fixed – and exact Bayesian inference otherwise. Free energy minimisation therefore provides a generic description of Bayesian inference and filtering (e.g., Kalman filtering). It is also used in Bayesian model selection, where free energy can be usefully decomposed into complexity and accuracy:

All Bayesian inference can be cast in terms of free energy minimisation; e.g.,. When free energy is minimised with respect to internal states, the Kullback–Leibler divergence between the variational and posterior density over hidden states is minimised. This corresponds to approximate Bayesian inference – when the form of the variational density is fixed – and exact Bayesian inference otherwise. Free energy minimisation therefore provides a generic description of Bayesian inference and filtering (e.g., Kalman filtering). It is also used in Bayesian model selection, where free energy can be usefully decomposed into complexity and accuracy:

所有的贝叶斯推断都可以以自由能量最小化的方式施放; 例如:。当自由能相对于内能态最小时，隐能态上变分密度和后密度之间的 Kullback-Leibler 散度最小。这相当于近似贝叶斯推断-当变分密度的形式是固定的-否则精确的贝叶斯推断。因此，自由能量最小化提供了一个通用的贝叶斯推断和滤波描述(例如，卡尔曼滤波)。它也用于贝叶斯模型选择，其中自由能可以有效地分解为复杂性和准确性:


[math]\displaystyle{ \underset{\text{free-energy}} {\underbrace{ F(s,\mu)}} = \underset{\text{complexity}} {\underbrace{ D_\mathrm{KL}[q(\psi\mid\mu)\parallel p(\psi\mid m)]}} - \underset{\mathrm{accuracy}} {\underbrace{E_q[\log p(s\mid\psi,m)]}} }[/math]
[math]\displaystyle{  \underset{\text{free-energy}} {\underbrace{ F(s,\mu)}} = \underset{\text{complexity}} {\underbrace{ D_\mathrm{KL}[q(\psi\mid\mu)\parallel p(\psi\mid m)]}} - \underset{\mathrm{accuracy}} {\underbrace{E_q[\log p(s\mid\psi,m)]}} }[/math]

数学下集{自由能}{底括号{ f (s，mu)}底括号{文本复杂度}{底括号{ d (psi，mid-mu)并行 p (psi，mid-m)}} -底括号{ e q [ log p (mid-psi，mid-psi)]}} / math


Models with minimum free energy provide an accurate explanation of data, under complexity costs (c.f., Occam's razor and more formal treatments of computational costs[21]). Here, complexity is the divergence between the variational density and prior beliefs about hidden states (i.e., the effective degrees of freedom used to explain the data).

Models with minimum free energy provide an accurate explanation of data, under complexity costs (c.f., Occam's razor and more formal treatments of computational costs). Here, complexity is the divergence between the variational density and prior beliefs about hidden states (i.e., the effective degrees of freedom used to explain the data).

在复杂性成本(c.f，Occam 的剃须刀和更正式的计算成本处理方法)下，自由能最小的模型提供了对数据的准确解释。在这里，复杂性是关于隐状态的变分密度和先验信念(即用于解释数据的有效自由度)之间的差异。


Free energy minimisation and thermodynamics

Variational free energy is an information theoretic functional and is distinct from thermodynamic (Helmholtz) free energy.[22] However, the complexity term of variational free energy shares the same fixed point as Helmholtz free energy (under the assumption the system is thermodynamically closed but not isolated). This is because if sensory perturbations are suspended (for a suitably long period of time), complexity is minimised (because accuracy can be neglected). At this point, the system is at equilibrium and internal states minimise Helmholtz free energy, by the principle of minimum energy.[23]

Variational free energy is an information theoretic functional and is distinct from thermodynamic (Helmholtz) free energy. However, the complexity term of variational free energy shares the same fixed point as Helmholtz free energy (under the assumption the system is thermodynamically closed but not isolated). This is because if sensory perturbations are suspended (for a suitably long period of time), complexity is minimised (because accuracy can be neglected). At this point, the system is at equilibrium and internal states minimise Helmholtz free energy, by the principle of minimum energy.

变分自由能是一种信息论泛函，不同于热力学(亥姆霍兹)自由能。然而，变分自由能的复杂性项与亥姆霍兹自由能有相同的固定点(假设系统是热力学闭合的，而不是孤立的)。这是因为如果感觉干扰暂停(适当长的时间) ，复杂性最小化(因为准确性可以忽略)。在这一点上，系统处于平衡状态，内部状态通过最小能量原理使亥姆霍兹自由能最小。


Free energy minimisation and information theory

Free energy minimisation is equivalent to maximising the mutual information between sensory states and internal states that parameterise the variational density (for a fixed entropy variational density).[11]模板:Better source This relates free energy minimization to the principle of minimum redundancy[24] and related treatments using information theory to describe optimal behaviour.引用错误：没有找到与</ref>对应的<ref>标签[25]

Perceptual neural organization: some approaches based on network models and information theory. Annu Rev Neurosci. , 13, 257–81.</ref>

[ https://www.annualreviews.org/doi/pdf/10.1146/annurev.ne.13.030190.001353感知神经组织: 基于网络模型和信息理论的一些方法]。神经科学。，13,257-81. / ref


Free energy minimisation in neuroscience

Free energy minimisation provides a useful way to formulate normative (Bayes optimal) models of neuronal inference and learning under uncertainty[26] and therefore subscribes to the Bayesian brain hypothesis.[27] The neuronal processes described by free energy minimisation depend on the nature of hidden states: [math]\displaystyle{ \Psi = X \times \Theta \times \Pi }[/math] that can comprise time-dependent variables, time-invariant parameters and the precision (inverse variance or temperature) of random fluctuations. Minimising variables, parameters, and precision correspond to inference, learning, and the encoding of uncertainty, respectively.

Free energy minimisation provides a useful way to formulate normative (Bayes optimal) models of neuronal inference and learning under uncertainty and therefore subscribes to the Bayesian brain hypothesis. The neuronal processes described by free energy minimisation depend on the nature of hidden states: [math]\displaystyle{ \Psi = X \times \Theta \times \Pi }[/math] that can comprise time-dependent variables, time-invariant parameters and the precision (inverse variance or temperature) of random fluctuations. Minimising variables, parameters, and precision correspond to inference, learning, and the encoding of uncertainty, respectively.

自由能最小化提供了一个有用的方式来建立规范(贝叶斯优化)模型的神经元推理和学习的不确定性，因此赞同贝叶斯大脑假说。自由能极小化描述的神经元过程依赖于隐状态的性质: math Psi x times Theta times Pi / math，它可以包含时间依赖的变量、时不变的参数和随机波动的精度(逆方差或温度)。最小化变量、参数和精度分别对应于推理、学习和不确定性的编码。


Perceptual inference and categorisation

Free energy minimisation formalises the notion of unconscious inference in perception[7][9] and provides a normative (Bayesian) theory of neuronal processing. The associated process theory of neuronal dynamics is based on minimising free energy through gradient descent. This corresponds to generalised Bayesian filtering (where ~ denotes a variable in generalised coordinates of motion and [math]\displaystyle{ D }[/math] is a derivative matrix operator):[28]

Free energy minimisation formalises the notion of unconscious inference in perception

自由能量最小化使知觉中的无意识推理的概念正规化


[math]\displaystyle{ \dot{\tilde{\mu}} = D \tilde{\mu} - \partial_{\mu}F(s,\mu)\Big|_{\mu = \tilde{\mu}} }[/math]
[math]\displaystyle{ \dot{\tilde{\mu}} = D \tilde{\mu} - \partial_{\mu}F(s,\mu)\Big|_{\mu = \tilde{\mu}} }[/math]

数学-部分数学 f (s，mu)-大数学


Usually, the generative models that define free energy are non-linear and hierarchical (like cortical hierarchies in the brain). Special cases of generalised filtering include Kalman filtering, which is formally equivalent to predictive coding[29] – a popular metaphor for message passing in the brain. Under hierarchical models, predictive coding involves the recurrent exchange of ascending (bottom-up) prediction errors and descending (top-down) predictions[30] that is consistent with the anatomy and physiology of sensory[31] and motor systems.[32]

Usually, the generative models that define free energy are non-linear and hierarchical (like cortical hierarchies in the brain). Special cases of generalised filtering include Kalman filtering, which is formally equivalent to predictive coding – a popular metaphor for message passing in the brain. Under hierarchical models, predictive coding involves the recurrent exchange of ascending (bottom-up) prediction errors and descending (top-down) predictions that is consistent with the anatomy and physiology of sensory and motor systems.

通常，定义自由能的生成模型是非线性和层次化的(就像大脑中的皮层层次)。广义滤波的特殊情况包括卡尔曼滤波，这在形式上等同于预测编码——一个流行的比喻信息在大脑中的传递。在层次模型中，预测编码涉及到反复出现的上升(自下而上)预测错误和下降(自上而下)预测，这与感觉和运动系统的解剖学和生理学一致。


Perceptual learning and memory

In predictive coding, optimising model parameters through a gradient ascent on the time integral of free energy (free action) reduces to associative or Hebbian plasticity and is associated with synaptic plasticity in the brain.

In predictive coding, optimising model parameters through a gradient ascent on the time integral of free energy (free action) reduces to associative or Hebbian plasticity and is associated with synaptic plasticity in the brain.

在预测编码中，通过自由能时间积分的梯度上升来优化模型参数可以降低为联想可塑性或赫布可塑性，并且与大脑中的突触可塑性有关。


Perceptual precision, attention and salience

Optimising the precision parameters corresponds to optimising the gain of prediction errors (c.f., Kalman gain). In neuronally plausible implementations of predictive coding,[30] this corresponds to optimising the excitability of superficial pyramidal cells and has been interpreted in terms of attentional gain.[33]

Optimising the precision parameters corresponds to optimising the gain of prediction errors (c.f., Kalman gain). In neuronally plausible implementations of predictive coding,

优化精度参数相当于优化预测误差的增益(cf，Kalman 增益)。在神经系统似是而非的预测编码实现中,


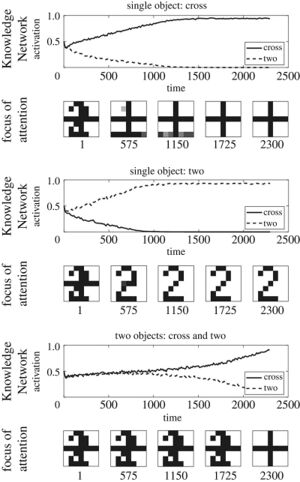
Simulation of the results achieved from a selective attention task carried out by the Bayesian reformulation of the SAIM entitled PE-SAIM in multiple objects environment. The graphs show the time course of the activation for the FOA and the two template units in the Knowledge Network.

Simulation of the results achieved from a selective attention task carried out by the Bayesian reformulation of the SAIM entitled PE-SAIM in multiple objects environment. The graphs show the time course of the activation for the FOA and the two template units in the Knowledge Network.

在多目标环境下，通过贝叶斯重构的 SAIM (pe-SAIM)对选择性注意任务的结果进行仿真。图表显示了知识网络中 FOA 和两个模板单元的激活时间过程。


Concerning the top-down vs bottom-up controversy that has been addressed as a major open problem of attention, a computational model has succeeded in illustrating the circulatory nature of reciprocation between top-down and bottom-up mechanisms. Using an established emergent model of attention, namely, SAIM, the authors suggested a model called PE-SAIM that in contrast to the standard version approaches the selective attention from a top-down stance. The model takes into account the forwarding prediction errors sent to the same level or a level above to minimize the energy function indicating the difference between data and its cause or in other words between the generative model and posterior. To enhance validity, they also incorporated the neural competition between the stimuli in their model. A notable feature of this model is the reformulation of the free energy function only in terms of predictions error in the course of task performance.

Concerning the top-down vs bottom-up controversy that has been addressed as a major open problem of attention, a computational model has succeeded in illustrating the circulatory nature of reciprocation between top-down and bottom-up mechanisms. Using an established emergent model of attention, namely, SAIM, the authors suggested a model called PE-SAIM that in contrast to the standard version approaches the selective attention from a top-down stance. The model takes into account the forwarding prediction errors sent to the same level or a level above to minimize the energy function indicating the difference between data and its cause or in other words between the generative model and posterior. To enhance validity, they also incorporated the neural competition between the stimuli in their model. A notable feature of this model is the reformulation of the free energy function only in terms of predictions error in the course of task performance.

关于自上而下和自下而上的争论，已经被作为一个主要的公开的注意力问题来处理，一个计算模型已经成功地阐明了循环的性质之间的互换自上而下和自下而上的机制。作者使用一个已经建立的突发注意模型，即 SAIM，提出了一个叫做 pe-SAIM 的模型，这个模型与标准版本相反，从一个自上而下的立场来处理选择性注意。该模型考虑到了前向预测错误发送到同一级别或以上级别，以最小化能量函数，表明数据和其原因之间的差异，或者换句话说，生成模型和后验之间的差异。为了提高效度，他们还在模型中加入了刺激之间的神经竞争。这个模型的一个显著特点是只根据任务执行过程中的预测误差来重新构造自由能函数。


[math]\displaystyle{ \dfrac{\partial E^{total}(Y^{VP},X^{SN},x^{CN},y^{KN})}{\partial y^{SN}_{mn}}=x^{CN}_{mn}-b^{CN}\varepsilon^{CN}_{nm}+b^{CN}\sum_{k}(\varepsilon^{KN}_{knm}) }[/math]

[math]\displaystyle{ \dfrac{\partial E^{total}(Y^{VP},X^{SN},x^{CN},y^{KN})}{\partial y^{SN}_{mn}}=x^{CN}_{mn}-b^{CN}\varepsilon^{CN}_{nm}+b^{CN}\sum_{k}(\varepsilon^{KN}_{knm}) }[/math]

数学部分 e ^ { total }(y ^ { VP } ，x ^ { SN } ，x ^ { CN } ，y ^ { KN })}{部分 y ^ { SN }} x ^ { CN }{ mn }-b ^ { CN }{ varepsilon ^ { nm } + b ^ { CN }{ sum { KN }{ knm }) / math


where, [math]\displaystyle{ E^{total} }[/math] is the total energy function of the neural networks entail, and [math]\displaystyle{ \varepsilon^{KN}_{knm} }[/math] is the prediction error between the generative model (prior) and posterior changing over time.[34])

where, [math]\displaystyle{ E^{total} }[/math] is the total energy function of the neural networks entail, and [math]\displaystyle{ \varepsilon^{KN}_{knm} }[/math] is the prediction error between the generative model (prior) and posterior changing over time.)

其中，数学 e ^ { total } / math 是神经网络的总能量函数，math varepsilon ^ { KN }{ knm } / math 是生成模型(prior)和后验随时间变化的预测误差

Comparing the two models reveals a notable similarity between the results as well as a promising finding, in that, in the standard version of SAIM, the model architecture consists of excitatory connections whereas in the PE-SAIM inhibitory connections will be leveraged in the course of Bayesian inference. The model has also been shown fit to predict the EEG and fMRI data drawn from human experiments.

Comparing the two models reveals a notable similarity between the results as well as a promising finding, in that, in the standard version of SAIM, the model architecture consists of excitatory connections whereas in the PE-SAIM inhibitory connections will be leveraged in the course of Bayesian inference. The model has also been shown fit to predict the EEG and fMRI data drawn from human experiments.

比较这两个模型揭示了结果之间的显著相似性和一个有希望的发现，在标准版本的 SAIM 中，模型结构由兴奋性连接组成，而在 pe-SAIM 抑制性连接将在贝叶斯推断过程中被利用。该模型也被证明适合于预测从人体实验中获得的脑电图和功能磁共振成像数据。


Active inference

When gradient descent is applied to action [math]\displaystyle{ \dot{a} = -\partial_aF(s,\tilde{\mu}) }[/math], motor control can be understood in terms of classical reflex arcs that are engaged by descending (corticospinal) predictions. This provides a formalism that generalizes the equilibrium point solution – to the degrees of freedom problem[35] – to movement trajectories.

When gradient descent is applied to action [math]\displaystyle{ \dot{a} = -\partial_aF(s,\tilde{\mu}) }[/math], motor control can be understood in terms of classical reflex arcs that are engaged by descending (corticospinal) predictions. This provides a formalism that generalizes the equilibrium point solution – to the degrees of freedom problem – to movement trajectories.

当梯度下降法应用于动作数学(s，tilde) / 数学时，运动控制可以通过传统反射弧来理解，传统反射弧是通过皮质脊髓神经递质的预测来实现的。这提供了一个形式化的概括的平衡点解决方案-自由度问题-运动轨迹。


Active inference and optimal control

Active inference is related to optimal control by replacing value or cost-to-go functions with prior beliefs about state transitions or flow.[36] This exploits the close connection between Bayesian filtering and the solution to the Bellman equation. However, active inference starts with (priors over) flow [math]\displaystyle{ f = \Gamma \cdot \nabla V + \nabla \times W }[/math] that are specified with scalar [math]\displaystyle{ V(x) }[/math] and vector [math]\displaystyle{ W(x) }[/math] value functions of state space (c.f., the Helmholtz decomposition). Here, [math]\displaystyle{ \Gamma }[/math] is the amplitude of random fluctuations and cost is [math]\displaystyle{ c(x) = f \cdot \nabla V + \nabla \cdot \Gamma \cdot V }[/math]. The priors over flow [math]\displaystyle{ p(\tilde{x}\mid m) }[/math] induce a prior over states [math]\displaystyle{ p(x\mid m) = \exp (V(x)) }[/math] that is the solution to the appropriate forward Kolmogorov equations.[37] In contrast, optimal control optimises the flow, given a cost function, under the assumption that [math]\displaystyle{ W = 0 }[/math] (i.e., the flow is curl free or has detailed balance). Usually, this entails solving backward Kolmogorov equations.[38]

Active inference is related to optimal control by replacing value or cost-to-go functions with prior beliefs about state transitions or flow. This exploits the close connection between Bayesian filtering and the solution to the Bellman equation. However, active inference starts with (priors over) flow [math]\displaystyle{ f = \Gamma \cdot \nabla V + \nabla \times W }[/math] that are specified with scalar [math]\displaystyle{ V(x) }[/math] and vector [math]\displaystyle{ W(x) }[/math] value functions of state space (c.f., the Helmholtz decomposition). Here, [math]\displaystyle{ \Gamma }[/math] is the amplitude of random fluctuations and cost is [math]\displaystyle{ c(x) = f \cdot \nabla V + \nabla \cdot \Gamma \cdot V }[/math]. The priors over flow [math]\displaystyle{ p(\tilde{x}\mid m) }[/math] induce a prior over states [math]\displaystyle{ p(x\mid m) = \exp (V(x)) }[/math] that is the solution to the appropriate forward Kolmogorov equations. In contrast, optimal control optimises the flow, given a cost function, under the assumption that [math]\displaystyle{ W = 0 }[/math] (i.e., the flow is curl free or has detailed balance). Usually, this entails solving backward Kolmogorov equations.

主动推理与最优控制相关，通过用关于状态转换或流的先验信念替换值函数或外推成本函数。这利用了贝叶斯过滤和贝尔曼方程的解决方案之间的紧密联系。然而，主动推理从流数学 f Gamma cdot nabla v + nabla 乘以 w / math 开始，这些数学由状态空间的标量数学 v (x) / 数学和向量数学 w (x) / 数学值函数(c.f，亥姆霍兹分解)指定。这里，math Gamma / math 是随机波动的振幅，代价是 math c (x) f cdot nabla v + cdot cdot cdot v / math。流上的先验数学 p (tilde { mid m) / math 导出了一个状态上的先验数学 p (x mid m) exp (v (x)) / math，这是适当的前向 Kolmogorov 方程的解。相比之下，给定一个成本函数，在数学 w / math 的假设下，最优控制使流量最优化(例如，流量是无旋度的或具有详细的平衡)。通常，这需要求解向后的 Kolmogorov 方程。


Active inference and optimal decision (game) theory

Optimal decision problems (usually formulated as partially observable Markov decision processes) are treated within active inference by absorbing utility functions into prior beliefs. In this setting, states that have a high utility (low cost) are states an agent expects to occupy. By equipping the generative model with hidden states that model control, policies (control sequences) that minimise variational free energy lead to high utility states.[39]

Optimal decision problems (usually formulated as partially observable Markov decision processes) are treated within active inference by absorbing utility functions into prior beliefs. In this setting, states that have a high utility (low cost) are states an agent expects to occupy. By equipping the generative model with hidden states that model control, policies (control sequences) that minimise variational free energy lead to high utility states.

最优决策问题(通常表示为部分可观测的马尔可夫决策过程)在主动推理中通过吸收效用函数到先验信念来处理。在此设置中，具有高效用(低成本)的状态是代理期望占据的状态。通过给生成模型装备隐藏状态，模型控制，政策(控制序列) ，最小化变化的自由能，导致高效用状态。


Neurobiologically, neuromodulators like dopamine are considered to report the precision of prediction errors by modulating the gain of principal cells encoding prediction error.[40] This is closely related to – but formally distinct from – the role of dopamine in reporting prediction errors per se[41] and related computational accounts.[42]

Neurobiologically, neuromodulators like dopamine are considered to report the precision of prediction errors by modulating the gain of principal cells encoding prediction error. This is closely related to – but formally distinct from – the role of dopamine in reporting prediction errors per se and related computational accounts.

神经生物学研究认为，多巴胺等神经调质通过调节主细胞编码预测错误的增益来报告预测错误的准确性。这与多巴胺在报告预测错误本身和相关的计算机账户中的作用密切相关，但在形式上有所不同。


Active inference and cognitive neuroscience

Active inference has been used to address a range of issues in cognitive neuroscience, brain function and neuropsychiatry, including: action observation,[43] mirror neurons,[44] saccades and visual search,[45][46] eye movements,[47] sleep,[48] illusions,[49] attention,[33] action selection,[40] consciousness,[50][51] hysteria[52] and psychosis.[53]

Active inference has been used to address a range of issues in cognitive neuroscience, brain function and neuropsychiatry, including: action observation, mirror neurons, saccades and visual search, eye movements, sleep, illusions, attention, hysteria and psychosis.

主动推理已经被用来解决一系列的问题，包括认知神经科学，大脑功能和神经精神病学，包括: 行为观察，镜像神经元，扫视和视觉搜索，眼球运动，睡眠，幻觉，注意力，歇斯底里和精神病。


See also


References

  1. ↑ Ashby, W. R. (1962). Principles of the self-organizing system.in Principles of Self-Organization: Transactions of the University of Illinois Symposium, H. Von Foerster and G. W. Zopf, Jr. (eds.), Pergamon Press: London, UK, pp. 255–278.
  2. ↑ Friston, Karl; Kilner, James; Harrison, Lee (2006). "A free energy principle for the brain" (PDF). Journal of Physiology-Paris. Elsevier BV. 100 (1–3): 70–87. doi:10.1016/j.jphysparis.2006.10.001. ISSN 0928-4257. PMID 17097864.
  3. ↑ 3.0 3.1 Shaun Raviv: The Genius Neuroscientist Who Might Hold the Key to True AI. In: Wired, 13. November 2018
  4. ↑ Freed, Peter (2010). "Research Digest". Neuropsychoanalysis. Informa UK Limited. 12 (1): 103–106. doi:10.1080/15294145.2010.10773634. ISSN 1529-4145.
  5. ↑ Colombo, Matteo; Wright, Cory (2018-09-10). "First principles in the life sciences: the free-energy principle, organicism, and mechanism". Synthese. Springer Science and Business Media LLC. doi:10.1007/s11229-018-01932-w. ISSN 0039-7857.
  6. ↑ Friston, Karl (2018). "Of woodlice and men: A Bayesian account of cognition, life and consciousness. An interview with Karl Friston (by Martin Fortier & Daniel Friedman)". ALIUS Bulletin. 2: 17–43.
  7. ↑ 7.0 7.1 Helmholtz, H. (1866/1962). Concerning the perceptions in general. In Treatise on physiological optics (J. Southall, Trans., 3rd ed., Vol. III). New York: Dover.
  8. ↑ Gregory, R. L. (1980-07-08). "Perceptions as hypotheses". Philosophical Transactions of the Royal Society of London. B, Biological Sciences. The Royal Society. 290 (1038): 181–197. Bibcode:1980RSPTB.290..181G. doi:10.1098/rstb.1980.0090. ISSN 0080-4622. JSTOR 2395424. PMID 6106237.
  9. ↑ 9.0 9.1 9.2 Dayan, Peter; Hinton, Geoffrey E.; Neal, Radford M.; Zemel, Richard S. (1995). "The Helmholtz Machine" (PDF). Neural Computation. MIT Press - Journals. 7 (5): 889–904. doi:10.1162/neco.1995.7.5.889. ISSN 0899-7667. PMID 7584891.
  10. ↑ Beal, M. J. (2003). Variational Algorithms for Approximate Bayesian Inference. Ph.D. Thesis, University College London.
  11. ↑ 11.0 11.1 Karl, Friston (2012-10-31). "A Free Energy Principle for Biological Systems" (PDF). Entropy. MDPI AG. 14 (11): 2100–2121. Bibcode:2012Entrp..14.2100K. doi:10.3390/e14112100. ISSN 1099-4300. PMC 3510653. PMID 23204829.
  12. ↑ Colombo, Matteo; Wright, Cory (2018-09-10). "First principles in the life sciences: the free-energy principle, organicism, and mechanism". Synthese. Springer Science and Business Media LLC. doi:10.1007/s11229-018-01932-w. ISSN 0039-7857.
  13. ↑ Conant, R. C., & Ashby, R. W. (1970). Every Good Regulator of a system must be a model of that system. Int. J. Systems Sci. , 1 (2), 89–97.
  14. ↑ Kauffman, S. (1993). The Origins of Order: Self-Organization and Selection in Evolution. Oxford: Oxford University Press.
  15. ↑ Nicolis, G., & Prigogine, I. (1977). Self-organization in non-equilibrium systems. New York: John Wiley.
  16. ↑ Maturana, H. R., & Varela, F. (1980). Autopoiesis: the organization of the living. In V. F. Maturana HR (Ed.), Autopoiesis and Cognition. Dordrecht, Netherlands: Reidel.
  17. ↑ Haken, H. (1983). Synergetics: An introduction. Non-equilibrium phase transition and self-organisation in physics, chemistry and biology (3rd ed.). Berlin: Springer Verlag.
  18. ↑ Jaynes, E. T. (1957). Information Theory and Statistical Mechanics. Physical Review Series II, 106 (4), 620–30.
  19. ↑ Crauel, H., & Flandoli, F. (1994). Attractors for random dynamical systems. Probab Theory Relat Fields, 100, 365–393.
  20. ↑ Roweis, S., & Ghahramani, Z. (1999). A unifying review of linear Gaussian models. Neural Computat. , 11 (2), 305–45. doi:10.1162/089976699300016674
  21. ↑ Ortega, P. A., & Braun, D. A. (2012). Thermodynamics as a theory of decision-making with information processing costs. Proceedings of the Royal Society A, vol. 469, no. 2153 (20120683) .
  22. ↑ Evans, D. J. (2003). A non-equilibrium free energy theorem for deterministic systems. Molecular Physics , 101, 15551–4.
  23. ↑ Jarzynski, C. (1997). Nonequilibrium equality for free energy differences. Phys. Rev. Lett., 78, 2690.
  24. ↑ Barlow, H. (1961). Possible principles underlying the transformations of sensory messages -{zh-cn:互联网档案馆; zh-tw:網際網路檔案館; zh-hk:互聯網檔案館;}-的存檔，存档日期2012-06-03.. In W. Rosenblith (Ed.), Sensory Communication (pp. 217-34). Cambridge, MA: MIT Press.
  25. ↑ Bialek, W., Nemenman, I., & Tishby, N. (2001). Predictability, complexity, and learning. Neural Computat., 13 (11), 2409–63.
  26. ↑ Friston, K. (2010). The free-energy principle: a unified brain theory? Nat Rev Neurosci. , 11 (2), 127–38.
  27. ↑ Knill, D. C., & Pouget, A. (2004). The Bayesian brain: the role of uncertainty in neural coding and computation. Trends Neurosci. , 27 (12), 712–9.
  28. ↑ Friston, K., Stephan, K., Li, B., & Daunizeau, J. (2010). Generalised Filtering. Mathematical Problems in Engineering, vol., 2010, 621670
  29. ↑ Rao, R. P., & Ballard, D. H. (1999). Predictive coding in the visual cortex: a functional interpretation of some extra-classical receptive-field effects. Nat Neurosci. , 2 (1), 79–87.
  30. ↑ 30.0 30.1 Mumford, D. (1992). On the computational architecture of the neocortex. II. Biol. Cybern. , 66, 241–51.
  31. ↑ Bastos, A. M., Usrey, W. M., Adams, R. A., Mangun, G. R., Fries, P., & Friston, K. J. (2012). Canonical microcircuits for predictive coding. Neuron , 76 (4), 695–711.
  32. ↑ Adams, R. A., Shipp, S., & Friston, K. J. (2013). Predictions not commands: active inference in the motor system. Brain Struct Funct. , 218 (3), 611–43
  33. ↑ 33.0 33.1 Feldman, H., & Friston, K. J. (2010). Attention, uncertainty, and free-energy. Frontiers in Human Neuroscience, 4, 215.
  34. ↑ Abadi K.A., Yahya K., Amini M., Heinke D. & Friston, K. J. (2019). Excitatory versus inhibitory feedback in Bayesian formulations of scene construction. 16 R. Soc. Interface
  35. ↑ Feldman, A. G., & Levin, M. F. (1995). The origin and use of positional frames of reference in motor control. Behav Brain Sci. , 18, 723–806.
  36. ↑ Friston, K., (2011). What is optimal about motor control?. Neuron, 72(3), 488–98.
  37. ↑ Friston, K., & Ao, P. (2012). Free-energy, value and attractors. Computational and mathematical methods in medicine, 2012, 937860.
  38. ↑ Kappen, H., (2005). Path integrals and symmetry breaking for optimal control theory. Journal of Statistical Mechanics: Theory and Experiment, 11, p. P11011.
  39. ↑ Friston, K., Samothrakis, S. & Montague, R., (2012). Active inference and agency: optimal control without cost functions. Biol. Cybernetics, 106(8–9), 523–41.
  40. ↑ 40.0 40.1 Friston, K. J. Shiner T, FitzGerald T, Galea JM, Adams R, Brown H, Dolan RJ, Moran R, Stephan KE, Bestmann S. (2012). Dopamine, affordance and active inference. PLoS Comput. Biol., 8(1), p. e1002327.
  41. ↑ Fiorillo, C. D., Tobler, P. N. & Schultz, W., (2003). Discrete coding of reward probability and uncertainty by dopamine neurons. Science, 299(5614), 1898–902.
  42. ↑ Frank, M. J., (2005). Dynamic dopamine modulation in the basal ganglia: a neurocomputational account of cognitive deficits in medicated and nonmedicated Parkinsonism. J Cogn Neurosci., Jan, 1, 51–72.
  43. ↑ Friston, K., Mattout, J. & Kilner, J., (2011). Action understanding and active inference. Biol Cybern., 104, 137–160.
  44. ↑ Kilner, J. M., Friston, K. J. & Frith, C. D., (2007). Predictive coding: an account of the mirror neuron system. Cogn Process., 8(3), pp. 159–66.
  45. ↑ Friston, K., Adams, R. A., Perrinet, L. & Breakspear, M., (2012). Perceptions as hypotheses: saccades as experiments. Front Psychol., 3, 151.
  46. ↑ Mirza, M., Adams, R., Mathys, C., Friston, K. (2018). Human visual exploration reduces uncertainty about the sensed world. PLoS One, 13(1): e0190429
  47. ↑ Perrinet L, Adams R, Friston, K. Active inference, eye movements and oculomotor delays. Biological Cybernetics, 108(6):777-801, 2014.
  48. ↑ Hobson, J. A. & Friston, K. J., (2012). Waking and dreaming consciousness: Neurobiological and functional considerations. Prog Neurobiol, 98(1), pp. 82–98.
  49. ↑ Brown, H., & Friston, K. J. (2012). Free-energy and illusions: the cornsweet effect. Front Psychol , 3, 43.
  50. ↑ Rudrauf, David; Bennequin, Daniel; Granic, Isabela; Landini, Gregory; Friston, Karl; Williford, Kenneth (2017-09-07). "A mathematical model of embodied consciousness". Journal of Theoretical Biology. 428: 106–131. doi:10.1016/j.jtbi.2017.05.032. ISSN 0022-5193. PMID 28554611.
  51. ↑ K, Williford; D, Bennequin; K, Friston; D, Rudrauf (2018-12-17). "The Projective Consciousness Model and Phenomenal Selfhood". Frontiers in Psychology (in English). 9: 2571. doi:10.3389/fpsyg.2018.02571. PMC 6304424. PMID 30618988.
  52. ↑ Edwards, M. J., Adams, R. A., Brown, H., Pareés, I., & Friston, K. J. (2012). A Bayesian account of 'hysteria'. Brain , 135(Pt 11):3495–512.
  53. ↑ Adams RA, Perrinet LU, Friston K. (2012). Smooth pursuit and visual occlusion: active inference and oculomotor control in schizophrenia. PLoS One. , 12;7(10):e47502


External links

Category:Biological systems

类别: 生物系统

Category:Systems theory

范畴: 系统论

Category:Computational neuroscience

类别: 计算神经科学

Category:Mathematical and theoretical biology

类别: 数学和理论生物学


This page was moved from wikipedia:en:Free energy principle. Its edit history can be viewed at 自由能原理/edithistory

取自“https://wiki.swarma.org/index.php?title=自由能原理&oldid=7225”