链路预测
链路预测 Link Prediction是指如何通过已知的网络节点以及网络结构等信息,预测网络中尚未产生连边的两个节点之间产生连接的可能性。这种预测既包含了对未知链接 Existing yet unknown link,也称丢失链接 Missing link 的预测,也包含了对未来链接 Future link 的预测。
链路预测是将复杂网络与信息科学联系起来的重要桥梁之一,它所要处理的是信息科学中最基本的问题——缺失信息的还原与预测。链路预测相关研究不仅能够推动网络科学和信息科学理论上的发展,而且具有巨大的实际应用价值,譬如可以知道蛋白质相互作用实验、进行在线社交推荐、找出交通传输网络中有特别重要作用的连边等。
研究方法
基于相似性的链路预测
- 基于局部信息的相似性指标
社会网络分析中经典的三元闭包 Triadic closure 原则指出,如果A、B 两个人拥有一个共同的朋友C,那么这两个人今后也很有可能成为朋友,从而使得3个节点构成一个闭合的三角形ABC。对于一般的网络,我们可以把这一原则推广如下:两个节点的共同邻居越多,这两个节点就越相似,从而更倾向于相互连接。最简单的基于共同邻居 Common neighbors 的节点相似性指标定义如下: [math]\displaystyle{ s_{xy}^{CN} = |Γ(x)| \cap |Γ(y)| }[/math]
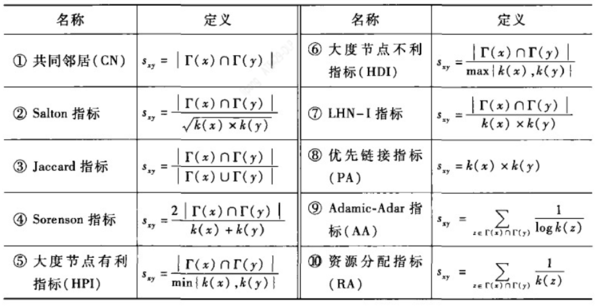
在相似性指标定义的基础上,还可以考虑两个节点的共同邻居的相对数量。下表列出了10种基于节点局部信息的相似性指标,第1种是计算共同邻居相似度的基本公式,其中第2至7种相似性指标是直接基于共同邻居指标的不同的规范化而得到的,表中的 k(x) = |Γ(x)| 为节点x的度。第8种指标PA是基于BA无标度网络模型中新加入节点倾向于和度大的节点相连的优先连接机制而提出的。
第9种指标AA的基本思想是度小的共同邻居节点的贡献大于度大的共同邻居节点,因此根据共同邻居节点的度为每个节点赋予一个权重值。这一点很容易理解,例如在微博中受关注较多的人往往是某个领域的专家或名人,因此共同关注他们的人之间可能并不拥有特别相似的兴趣——一个中学生和一个企业家都有可能是姚晨的粉丝。相反,如果两个人共同关注了一个粉丝很少的人(非名人),那么说明这两个人确实具有相同的兴趣爱好或者重叠的社交圈,因此有更高概率相连。又如在推荐系统中,共同购买冷门产品的两个用户往往比共同购买热门产品的用户更相似。
| 名称 | 定义 | 名称 | 定义 |
|---|---|---|---|
| (1)共同邻居(CN) | [math]\displaystyle{ s_{xy}^{CN} = |Γ(x)| \cap |Γ(y)| }[/math] | (6)大度节点不利指标(HDI) | [math]\displaystyle{ s_{xy}=\frac{2 x |Γ(x)| \cap |Γ(y)|}{max\{k_x,k_y\}} }[/math] |
第10种指标RA是受网络资源分配过程的启发,周涛等人提出的“资源分配指标 Resource allocation”,其与AA指标有异曲同工之妙。RA和AA指标最大的区别就在于赋予共同邻居节点权重的方式不同,前者是以 1/k 的形式递减,后者是以 1/logk 的形式递减。可见,当网络的平均度较小时,RA和AA差别不大;但是当平均度较大时,就有很大的区别了。研究显示,RA指标在刻画加权网络和社区挖掘应用中的表现胜过AA指标,图灵奖得主Hopdroft的一篇论文也显示,可以利用社区等中观结构信息改进局部指标,其中RA指标改进后的效果最佳。
- 基于路径的相似性指标
基于共同邻居的相似性指标的优势在于计算复杂度较低,但是由于使用的信息非常有限,预测精度受到限制,因此发展出了基于路径的相似性指标,主要有3个,分别是局部路径指标 Local path 、Katz指标和LHN-II指标。
1.局部路径指标
周涛等人在共同邻居的基础上考虑三阶路径的因素,提出了基于局部路径的相似性指标,其定义为 [math]\displaystyle{ S=A^2+\alpha A^3 }[/math]
其中[math]\displaystyle{ \alpha }[/math] 为可调参数,A 表示网络的邻接矩阵, [math]\displaystyle{ (A^3)_{xy} }[/math]表示节点 [math]\displaystyle{ V_x }[/math] 和 [math]\displaystyle{ V_y }[/math] 之间长度为3的路径数目。当[math]\displaystyle{ \alpha }[/math] = 0时,LP指标就退化为 CN 指标。 CN 指标本质上也可看成基于路径的指标,只是它仅考虑了二阶路径数目。局部路径指标可以扩展为更高阶的情形,即考虑n阶路径的情况:
[math]\displaystyle{ S^n=A^2+\alpha\cdot A^3+\alpha^2\cdot A^4+\cdots +\alpha^{n-2}\cdot A^n }[/math]
随着 n 的增加,局部路径指标的计算复杂度越来越大。一般而言,考虑 n 阶路径的计算复杂度为O(N<k>^n)。但是当 n 趋于无穷大的时候,局部路径指标相当于考虑网络全部路径的Katz指标,此时计算量反而有可能下降,因为可转变为计算矩阵的逆。
2.Katz指标
Katz指标考虑了所有网络的路径,因此其定义为:
[math]\displaystyle{ S_{xy}=\sum_{l=1}^{\infty }\alpha^l\cdot\left | paths_{x,y}^{\lt l\gt } \right |= \alpha A_{xy}+\alpha^2\cdot (A^2)_{xy}+\alpha^3\cdot (A^3)_{xy}+\cdots }[/math]
其中[math]\displaystyle{ \alpha \gt 0 }[/math] 为控制路径权重的可调参数,[math]\displaystyle{ \left | paths_{x,y}^{\lt l\gt } \right | }[/math]表示连接节点 [math]\displaystyle{ V_x }[/math]和 [math]\displaystyle{ V_y }[/math] 的路径中长度为 l 的路径数。要使上述级数收敛,则参数[math]\displaystyle{ \alpha }[/math] 应小于邻接矩阵最大特征值的倒数,此定义还可以表示为:
[math]\displaystyle{ S = (I - \alpha\cdot A)^{-1} - I }[/math]
显然,当参数[math]\displaystyle{ \alpha }[/math] 很小时,高阶路径的贡献也较小,使得 Katz 指标的预测结果接近于局部路径指标。
3.LHN-II指标
LHN-II 指标是 Leicht,Holme 和 Newman 提出的另一种相似性计算方法,他的基本思想是基于一般等价 Regular equivalence 提出的。与结构等价不同,一般等价的定义更广泛。在一般等价的定义下,如果两个节点所连接的节点之间相似,那么这两个节点也相似,即使它们之间没有共同的邻居节点。
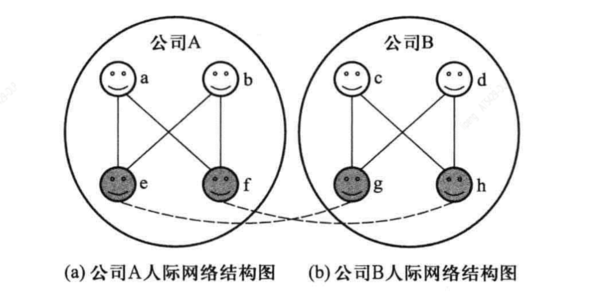
下图给出了一个简单的例子来帮助我们理解结构等价和一般等价的区别。根据结构等价的定义,在公司A内部,由于员工a和员工b都认识员工e和员工f(即它们有两个共同邻居节点),于是称员工a和员工b是结构等价的。同理,员工e和员工f也是结构等价的,同样地,在公司B中,员工c和员工d是结构等价的,员工g和员工h也是结构等价的。现在考虑员工a和员工c是否相似?根据一般等价的定义,由于员工a连接的节点e、f与员工c连接的节点g、h分别是相似的,那么我们可以认为员工a和员工c也是相似的,同理,在一般等价的意义下,员工b和员工d也是相似。从这个例子可以看出,结构相似性或称结构等价更强调的是两个节点是否在同一个环境下,也就是说是否连接了相同的节点;然而一般等价考虑的是这两个节点是否处于同样的角色,即使他们没有相同的邻居节点,但是由于各自的邻居节点之间本身相似,这两个节点也相似。一般等价意义下的相似性是LHN-II指标的核心。
从一般等价的角度考虑,LHN-II指标认为如果两个节点的邻居节点之间是相似的,那么这两个节点也是相似的。它与Katz指标的区别主要是把Katz指标中的[math]\displaystyle{ (A^{n})_{xy} }[/math]变成 [math]\displaystyle{ (A^{n})_{xy} }[/math] 的期望值,注意到 [math]\displaystyle{ (A^{n})_{xy} }[/math] 的期望值为 [math]\displaystyle{ E\left [ (A^l)_{xy} \right ]=\frac{k_xk_y}{M}\lambda _1^{l-1} }[/math]
其中[math]\displaystyle{ \lambda_1 }[/math]为矩阵A的最大特征值,则LHN-II指标的表达式如下:
[math]\displaystyle{ S_{xy}^{LHN2}=\delta _{xy} + \sum_{l=1}^{\infty }\Phi ^l \frac{(A^l)_{xy}}{E\left [ (A^l)_{xy} \right ]} =\delta _{xy} + \frac{2M}{k_xk_y}\sum_{l=1}^{\infty }\Phi ^l\lambda _1^{1-l}(A^l)_{xy} =\left [ 1 - \frac{2 M \lambda_1}{k_xk_y} \right ]\delta _{xy} + \frac{2 M \lambda_1}{k_xk_y}\left [ (I-\frac{\Phi}{\lambda_1} A )^{-1} \right ]_{xy} }[/math]
其中[math]\displaystyle{ \delta _{xy} }[/math]为 Kronecker [math]\displaystyle{ \delta }[/math] 函数,[math]\displaystyle{ \Phi }[/math] 为取值小于1的参数。上式最后一个等式的第一项是可以去掉的对角阵,从而相似性矩阵可以写为
[math]\displaystyle{ S=2M\lambda_1D^{-1}(I-\frac{\Phi A}{\lambda_1})^{-1}D^{-1} }[/math]
其中D为度值矩阵,[math]\displaystyle{ D_{xy} = \delta_{xy} \cdot k_{x} }[/math]。
- 基于随机游走的节点相似性指标
还有相当数量的相似性指标是基于随机游走过程定义的,包括平均通勤时间 Average commute time 、Cos+指标、有重启的随机游走 Random walk with restart、SimRank指标、局部随机游走指标 Local random walk 和有叠加效应的随机游走指标 Superposed random walk等。
1.平均通勤时间 ACT
设[math]\displaystyle{ m(x,y) }[/math] 为一个随机粒子从节点x到节点y平均需要走的步数,那么节点x和y的平均通勤时间定义为:[math]\displaystyle{ n(x , y) = m(x , y) + m(y , x) }[/math]
其数值解可通过求该网络拉普拉斯矩阵[math]\displaystyle{ L }[/math] 的伪逆[math]\displaystyle{ L^+ }[/math] 获得,即 [math]\displaystyle{ n(x,y)=M(l^+_{xx} +l^+_{yy} - 2l^+_{xy}) }[/math]
其中[math]\displaystyle{ l^{+}_{xy} }[/math]表示矩阵[math]\displaystyle{ L^+ }[/math]中相应位置的元素。如果两个节点的平均通勤时间越小,那么两个节点越进阶。由此,定义基于ACT的相似性为(在此可忽略常数M)
[math]\displaystyle{ s_{xy}^{ACT}=\frac{1}{l^+_{xx} +l^+_{yy} - 2l^+_{xy}} }[/math]
2.余弦相似性指标 Cos+指标
在由向量[math]\displaystyle{ v_x = \Lambda ^{1/2}U^{T}e_{x} }[/math]展开的欧式空间内,[math]\displaystyle{ L^+ }[/math]中的元素[math]\displaystyle{ l^{+}_{xy} }[/math]可表示为两向量[math]\displaystyle{ v_x }[/math]和[math]\displaystyle{ v_y }[/math]的内积,即[math]\displaystyle{ l^{+}_{xy} = v_{x}^{T} v_y }[/math],其中[math]\displaystyle{ U }[/math]是一个标准正交矩阵,由[math]\displaystyle{ L^+ }[/math]特征向量按照对应的特征根从大到小排列,[math]\displaystyle{ \Lambda }[/math]为以特征根为对角元素的对角矩阵,[math]\displaystyle{ e_{x} }[/math] 表示一个一维向量且只有第x个元素为1,其他都为0。由此定义余弦相似性如下:
s_{xy}^{cos+}=cos(x,y)^+=\frac{l_{xy}^+}{\sqrt{l^+_{xx} \cdot l^+_{yy}}}
3.重启的随机游走 RWR
这个指标可以看成是PageRank 算法的拓展应用。它假设随机游走粒子在每走一步的时候都以一定概率返回初始位置。设粒子返回概率为 1-c,[math]\displaystyle{ P }[/math] 为网络的马尔科夫概率转移矩阵,其元素 [math]\displaystyle{ P_{xy} = a_{xy}/k_{x} }[/math]表示节点x处的粒子下一步走到节点y的概率。其中如果节点x和节点y相连,则[math]\displaystyle{ a_{xy}=1 }[/math],否则[math]\displaystyle{ a_{xy}=0 }[/math]。某一粒子初始时刻在节点x处,那么t+1时刻该粒子到达网络各个节点的概率向量为 [math]\displaystyle{ q_{x}(t+1) = c \cdot P^{T}q_{x}(t) + (1-c) e_{x} }[/math]
其中[math]\displaystyle{ e_{x} }[/math]表示初始状态(其定义与Cos+中相同),上式的稳态解为[math]\displaystyle{ q_{x} = (1-c)(I-cP^{T})^{-1}e_{x} }[/math]
其中元素[math]\displaystyle{ q_{xy} }[/math]为从节点x出发的粒子最终有多少概率走到节点y。由此定义RWR相似性如下:
[math]\displaystyle{ s_{xy}^{RWR} = q_{xy} + q_{yx} }[/math]
4.SimRank指标 SimR
它的基本假设是,如果两节点所连接的节点相似,那么这两个节点就相似。其自洽定义式为
[math]\displaystyle{ s_{xy}^{simR}=C\frac{\sum_{v_z\in \Gamma (x)}\sum_{{v_z}'\in \Gamma (y)}s_{zz'}^{simR}}{k_xk_y} }[/math]
其中假定 [math]\displaystyle{ s_{xx} =1, C \in [0,1] }[/math]为相似性传递时的衰减参数。
SimR指标同时考虑了结构等价和一般等价。当节点x的邻居z同时也是节点y的邻居时,该指标考虑了结构等价;当节点x不等于节点y时,该指标概率了一般等价。可以证明,SimR指标可以用来描述两个分别从节点x和y出发的粒子平均过多久会相遇。
5.局部随机游走指标 LRW
上述4种随机游走指标是基于全局的随机游走,这类指标往往计算复杂度很高,因此很难在大规模网络上应用。刘伟平和吕琳媛提出了一种基于网络局部随机游走的相似性指标LRW,它只考虑有限步数的随机游走过程。一个粒子 t 时刻从节点x出发,定义[math]\displaystyle{ π_{xy} (t) }[/math]为 t+1 时刻这个粒子正好走到节点y的概率,那么可得到系统演化方程:
[math]\displaystyle{ \pi_{x} (t + 1) = P^T\pi_{x}(t),t=0,1,… }[/math]
其中[math]\displaystyle{ \pi_{x}(0) }[/math]为一个[math]\displaystyle{ Nx1 }[/math]的向量,只有第x 个元素为1,其他为0,即[math]\displaystyle{ \pi_{x}(0) =e_x }[/math]。设定各个节点的初始资源分布为[math]\displaystyle{ q_x }[/math],那么基于t步随机游走的相似性为
[math]\displaystyle{ s_{xy}^{LRW} = q_{xy} + q_{yx} }[/math]
6.叠加的局部随机游走指标 SRW
这个指标给邻近目标节点的点更多的机会与目标节点相连,充分考虑了很多真实网络连接上的局域性特点,它是在LRW的基础上,将t步及其以前的结果加总,便得到SRW的值,即:
[math]\displaystyle{ s_{xy}^{SRW}(t)=\sum_{t}^{l=1}s_{xy}^{LRW}(l) = q_x\sum_{t}^{l=1}\pi_{xy}(l) + q_y\sum_{t}^{l=1}\pi_{yx}(l) }[/math]
基于似然分析的链路预测
基于相似性的链路预测方法,是最简单的一种分析框架,除此之外,还有另一种最复杂的链路预测分析框架——基于似然分析的链路预测。这个框架本身远远复杂于基于相似性的框架,而且框架中的每一个组成成分自身都非常复杂,但这个框架下衍生出的算法除了给出链路预测的结果之外,还给出了我们对于网络结构的深刻洞见,例如“层次结构模型 Hierachical structure model”给出了网路层次组织形态的定量刻画,“随机分块模型 Stochastic block model”类似于社区分解一样把网络划分成了若干子块。这些对理解网络结构特征方面的贡献,是基于相似性的框架所不能提供的。
基于似然分析的链路预测的基本思路是:根据网络结构的产生和组织方式以及目前已经观察到的链路计算网络的似然值,并认为真实的网络使得网络似然值最大,然后再根据网络似然最大化计算每一对未连接的节点产生连边的可能性。
- 层次结构模型 HSM
层次结构模型假设真实的网络都存在某种层次性,网络的连接则可看作是这种内在层次结构的反映。该方法的计算步骤如下:
1.一个N个节点的网络可以用一个包含N个叶子节点的族谱树表示,这N个叶子节点将由N-1个非叶子节点连接起来,其中每个非叶子节点都有一个概率值,则两个叶子节点连接的概率就等于他们最近共同祖先节点的概率值。给定一个族谱树,将网络的似然值最大化,就可以得到非叶子节点的概率值,并由此计算出这一个族谱树所对应的网络最大的似然值。
2.使用马尔科夫链蒙特卡洛方法对网络不同的族谱树进行抽样,使得每个族谱树出现的频次正比于该树对应的最大的网络似然值。两个节点连边的概率就等于所有抽样出来的族谱树中两个节点连边概率的平均值。注意似然高的族谱树会出现多次,因此对这个平均概率的贡献也大。
3.把平均连边概率看做是相似性框架中的相似性指标[math]\displaystyle{ s_{xy} }[/math],按照这个值从大到小排序,排在前面的就是预测的连边。
需要指出的是,层次结构模型在处理具有明显层次结构的网络(如恐怖袭击网络和草原食物链)时具有较高的精确度,但在处理一般性网络时效果并不一定突出。
- 随机分块模型 SBM
与层次结构模型的思想类似,随机分块模型假设网络中的节点可以被分为若干集合,两个节点间连接的概率只与相应的集合有关。换句话说,同一个群众所有节点的地位是相同的。随机分块模型特别适合刻画节点所属群的成员身份对于其连接行为有关键影响的情况,例如,著名的“角色模型”就包含了随机分块模型的理念。
随机分块模型的效果要好于层次结构模型。同时,该方法还可以剔除网络的错误连边,如纠正蛋白质相互作用网络中的错误连边。
- 闭路模型 Loop model
似然分析的更一般的框架是:给定一个网络系统,特定网络哈密顿量的负指数被统计分配函数归一化后,就得到这个网络出现的似然,一条未被观察到的连边存在的可能性就等于添加这条连边后网络的似然值。闭路模型考虑网络结构形成中的“局部性原则”,并由此定义了网络的哈密顿量。实验表明,闭路模型的预测精度大于层次结构模型和随机分块模型。
基于机器学习的链路预测
用机器学习的思路进行链路预测,主要分为基于特征分类方法、基于概率图模型方法和基于矩阵分解方法三大类。
- 基于特征分类方法
网络中的链路预测问题可以看成机器学习中的分类问题,其中每个数据点对应一对节点之间关系的标记,假定两个节点之间存在连边,则数据点的值为+1,否则为-1。特征选取是分类问题中最重要的问题之一,目前研究较多的主要包括基于节点与边的属性特征和基于节点所处网络的拓扑结构特征(如CN、AA、Katz、最短路径)等。哈桑 Hasan 等人提取合著网络中科学家研究领域的关键词作为特征,用监督学习中一些常用的分类算法(如决策树、K近邻法、多层感知器、支持向量机、径向基网络)对缺失的连边进行较为精准的预测,其中以支持向量机方法表现最佳。
- 基于概率图模型
基于概率图模型的链路预测方法使用图模型来表达节点之间的连边概率,根据模型中概率依赖关系,可分为有向无环的贝叶斯网络和无向的马尔科夫网络。随机分块模型和层次结构模型分别是典型的基于贝叶斯网络和基于马尔科夫网络的链路预测方法。基于概率图模型的链路预测方法有很多,典型的还有有监督随机游走链路预测算法,将网络结构信息与节点和连边的属性信息结合起来,给每条边分配不同的转移概率。与其他有监督的机器学习方法相比,该算法无须知道网络的特征和相关的领域知识。
- 基于矩阵分解
基于矩阵分解的链路预测方法是基于网络邻接矩阵的代数谱变换而得到的方法,来预测网络中链路的存在性和链路的权值。相比其他几种机器学习方法,该方法要学习的参数少很多,但计算复杂度较高。链路预测问题可以视为邻接矩阵填充问题,并可以通过双线性回归模型将节点和链路的显特征和隐特征结合起来用矩阵分解方法解决。边缘去噪模型将根据给定关系矩阵求未知边或丢失边的问题变成一个矩阵降噪去噪问题。
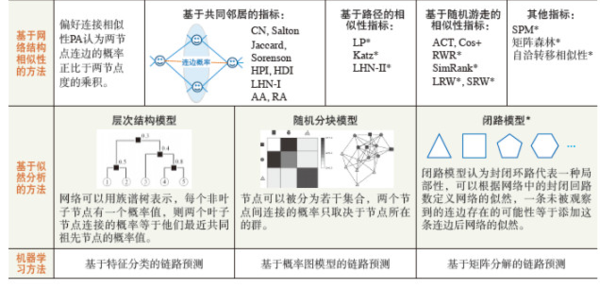
关于不同的链路预测研究方法的分类可以参考下表:
应用场景
链路预测有着广泛的应用场景:在生物领域,利用蛋白质间相互作用关系的结构信息进行链路预测,可以为实验的测定提前提供参考依据,从而降低实验成本、提高成功率;在社交网络领域,链路预测可以对社交网络中的好友关系、朋友推荐进行预测,从而提高用户对社交网站的体验满意度和使用黏性;在电子商务领域,除了传统的协同过滤推荐算法外,利用网络结构信息(如网络三角形结构)等特征进行商品推荐也取得了显著的优势;此外,通过识别隐藏的链边或异常的链边对信息不完全或含有噪音的网络进行重构,可以提高网络的传输能力,这对于航空网络重构有很大的启发意义。
除此之外,链路预测的算法和思想通过一些变换还可以用来解决一些看似没有太大关系的问题。例如,对疾病信号和股票指数的预测。基于链路预测的思想和方法,我们还可以设计基于节点相似性的社团划分以及对网络演化模型的定量化评估方法。链路预测还可以帮助提高节点标签预测的精度,特别是在已知标签节点稀疏的情况下效果显著。这一方法可以应用于判断一篇学术论文的类型,判断一本书的政治态度(中立、自由派或保守派),或者判断一个手机用户是否产生了更换电信运营商的念头。
代表人物
- 吕琳媛
吕琳媛主要研究方向为复杂网络信息挖掘领域,包括海量信息导航、挖掘、推荐和预测。目前担任阿里巴巴复杂科学研究中心副主任,中欧联合实验室执行主任,中国工业与应用数学学会复杂网络与系统控制专业委员会委员,杭州市特聘专家。
近年来主持/参与国家级项目5项(2016年获得国家自然科学基金优秀青年基金),省部级项目4项,横向课题4项。 在相关领域发表学术论文 50余篇,其中SCI论文39篇,总影响因子122,发表期刊包括Physics Reports,PNAS,Nature Communications等国际知名学术期刊。三篇论文入选ESI全球Top-1%高引用论文,论文SCI引用1200余次,谷歌学术引用3000余次,其中9篇论文引用超过100次。2013年出版学术专著《链路预测》获得第四届中国大学出版社图书奖优秀学术著作一等奖。申请发明专利12项。2015年荣获浙江省杰出青年基金,2014年荣获中国计算机学会自然科学二等奖,中国网络科学论坛青年希望奖,首届CCF-腾讯犀牛鸟基金优秀奖。
- 周涛
周涛主要从事复杂性科学和大数据挖掘算法和应用研究,先后攻克推荐系统准确性-多样性困境、复杂网络链路可预测性、H指数-度-核心度关系等图挖掘领域的重要难题,成果发表在PNAS, Nature Communications, Physics Reports, KDD和ICDM等国际顶尖期刊和会议上。目前论文google总引用超过14000次,其中8篇论文入选ESI高引用论文,H指数为57,2014和2015连续两年入选Elsevier最具国际影响力中国科学家名单。
因其在科学研究上的杰出表现,2011年获得第十二届中国青年科技奖(最年轻获奖者),2011年入选四川省“百人计划”,2012年获得国家首批优秀青年科学基金资助,2013年入选国家“万人计划”首批青年拔尖人才支持计划,2014年获得四川省科技进步一等奖、中国计算机学会自然科学奖,2015年获得共青团中央授予的“最美青年科技工作者”称号,并与屠呦呦等七名个人和北斗导航等三个团队共同当选2015年度中国十大科技创新人物。
- 马克·纽曼 Mark Newman
Newman是一名英裔美国物理学家,也是密歇根大学 University of Michigan 物理学系的阿纳托尔·拉波特 Anatol Rapoport 杰出教授,也是圣达菲研究所 Santa Fe Institute 的外部教员。他因在复杂网络和复杂系统领域的基础性贡献而闻名,为此他被授予2014年拉格朗日奖。
Newman以其对复杂网络的研究而著称,尤其是在科学家的协作模式,随机图论 Random graph theory,社区结构 Community structure,渗流理论 Percolation theory 和网络流行病学 Network epidemiology方面的工作。他作为共同发明人,与迈克尔·卡斯特 Michael Gastner 一起,发明了一种可以产生密度均衡地图 Density-equalizing maps 或统计地图 Cartograms的方法,该方法构成了Worldmapper网站的基础。他们的工作在2004年美国总统大选后受到关注,成为了当时被广泛传播的一种选举结果地图的基础,(他们)根据各州的人口数调整了州的规模,以便更准确地了解每个党派的选民投票人数。
- 克里斯托弗·大卫·摩尔 Cristopher David Moore
克里斯托弗·大卫·摩尔 Cristopher David Moore,也称为克里斯·摩尔 Cris Moore 是美国计算机科学家,数学家和物理学家。他是圣达菲研究所的驻校教师,曾任新墨西哥大学 University of New Mexico 的正教授。
1993年,Moore 发现了一种新颖的解决三体问题的方法,表明在牛顿力学中,三个等质量的物体有可能沿着一条八字形曲线、在同一条轨道相互跟随。Moore 在网络科学领域也很活跃,在该领域有许多著名的出版物。在与Clauset和Mark Newman的合作中,Moore开发了复杂网络的层次聚类概率模型,并表明他们的模型可以在面对网络连接结构发生变化时可靠地预测聚类结果。
- 亚伦·克劳斯特 Aaron Clauset
Aaron Clauset是一位美国计算机科学家,致力于网络科学,机器学习和复杂系统领域。目前,他在科罗拉多大学博尔德分校 University of Colorado Boulder 教授计算机科学,也是圣菲研究所的外部教员。
Clauset因与Cosma Shalizi和Mark Newman进行的合作研究而闻名,他们针对经验数据中是否存在幂律模式开发了严格的统计检验,并且证明了许多宣称符合幂律分布的网络实际上并不是幂律分布。他还因开发检测复杂网络中的社区结构算法的工作而著称,特别是和Newman、Moore合作发展的网络层次聚类模型。在其他方面,Clauslet 与麦克斯韦·扬 Maxwell Young 、克里斯蒂安·斯克雷德·格莱蒂奇 Kristian Skrede Gleditsch 共同完成了一些独特发现:世界范围内恐怖事件发生的频率和严重性服从幂律分布。
2015年,Clauset 因开发和评估一种网络结构特征的新方法而获得了美国国家科学基金会颁发的著名的CAREER奖。2016年,Clauset因在网络结构方面(包括Internet映射,推断缺失链接和社区结构),以及对人类冲突和社会分层所做的启发性分析方面做出的贡献而获得网络科学学会颁发的网络科学领域的Erdös-Rényi奖。
参考资料
- 汪小帆,李翔,陈关荣.《网络科学导论》.北京:高等教育出版社,2012年:178-186
- 吕琳媛,周涛.《链路预测》.北京:高等教育出版社,2013年:57-93
- 吕琳媛,任晓龙,周涛.《网络链路预测:概念与前沿》[J].《中国计算机学会通讯》,2016年,第4期
- Clauset A, Moore C, Newman M E J. Hierarchical structure and the prediction of missing links in networks [J]. Nature, 2008,453(7191): 98-101.
- [1]
- Link Prediction Group 网站:http://www.linkprediction.org/
编者推荐
- 链接预测可用于分析网络将如何发展,或者在给定信息不完整情况下来发现“丢失”的链接,对于这个问题,有研究者提出了一种新的,结合广义群贴近度中心性和半值相互作用指数的拟局部方法(即考虑半径k内节点的方法),详见 《链路预测的博弈算法》
- 深度学习已经成功地在图像识别、语音识别、自然语言处理、游戏与博弈等领域取得了突飞猛进的发展,并渗透到了我们的日常生活中。那么,我们有没有可能将这种技术借剪到复杂网 络的研究之中呢?近年来,人们凭借着网络嵌入(Network Embedding)、图卷积神经网络(Graph Convolutional Neural Network)、图注意力模型(Graph Attention Network)等新技术,已经开发了若干图结构上的深度学习算法,并取得了一定的成功应用。北师大系统科学学院教授、博导张江老师亲授《当复杂网络遇上机器学习》,将对这些算法以及应用,包括各式各样的网络嵌入算法、节点分类问题、链路预测问题、图分类问题、网络动力学预测问题等做一简单介绍,并对网络上的深度学习问题进行了展望。
- 网络上的注意力模型(Graph Attention Model)是一种通用的网络嵌入算法,它能够在节点分类、链路预测等问题上得到极高的精度。它可以模仿一个机器头对网络中的节点进行信息读取和分析,然后将综合的结果放到节点的向量中的过程。《网络上的注意力模型》课程将详细介绍这一模型及其应用。
本中文词条由木子二月鸟用户参与编译, 苏格兰用户审校,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。
- ↑ Sørensen, T, Sørensen, T A, Sørensen, T J (1948) A method of establishing groups of equal amplitude in plant sociology based on similarity of species content and its application to analyses of the vegetation on Danish commons.