无标度网络模型
此词条暂由彩云小译翻译,未经人工整理和审校,带来阅读不便,请见谅。
| Network science | ||||
|---|---|---|---|---|
| 模板:CSS image crop | ||||
| 模板:Hlist | ||||
| Network types | ||||
| Graphs | ||||
|
||||
| 模板:Hlist | ||||
| Models | ||||
|
||||
| 模板:Hlist | ||||
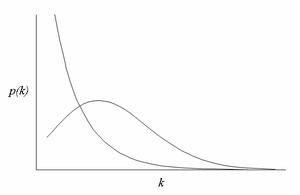
A scale-free network is a network whose degree distribution follows a power law, at least asymptotically. That is, the fraction P(k) of nodes in the network having k connections to other nodes goes for large values of k as
A scale-free network is a network whose degree distribution follows a power law, at least asymptotically. That is, the fraction P(k) of nodes in the network having k connections to other nodes goes for large values of k as
无尺度网络是一个度分布遵循幂律的网络,至少是渐近的。也就是说,网络中与其他节点有 k 个连接的节点的分数 p (k)代表大的 k 为
- [math]\displaystyle{ \lt math\gt 数学 P(k) \ \sim \ k^\boldsymbol{-\gamma} P(k) \ \sim \ k^\boldsymbol{-\gamma} P(k) \ \sim \ k^\boldsymbol{-\gamma} }[/math]
</math>
数学
where [math]\displaystyle{ \gamma }[/math] is a parameter whose value is typically in the range 2 < [math]\displaystyle{ \gamma }[/math] < 3 (wherein the second moment of [math]\displaystyle{ k^\boldsymbol{-\gamma} }[/math] is infinite but the first moment is finite), although occasionally it may lie outside these bounds.[1][2]
where [math]\displaystyle{ \gamma }[/math] is a parameter whose value is typically in the range 2 < [math]\displaystyle{ \gamma }[/math] < 3 (wherein the second moment of [math]\displaystyle{ k^\boldsymbol{-\gamma} }[/math] is infinite but the first moment is finite), although occasionally it may lie outside these bounds.
其中 math gamma / math 是一个参数,其值通常在2 math gamma / math 3范围内(其中 math k ^ boldsymbol {-gamma } / math 的第二个时刻是无限的,但第一个时刻是有限的) ,尽管有时它可能位于这些界限之外。
Many networks have been reported to be scale-free, although statistical analysis has refuted many of these claims and seriously questioned others.[3][4] Preferential attachment and the fitness model have been proposed as mechanisms to explain conjectured power law degree distributions in real networks.
Many networks have been reported to be scale-free, although statistical analysis has refuted many of these claims and seriously questioned others. Preferential attachment and the fitness model have been proposed as mechanisms to explain conjectured power law degree distributions in real networks.
据报告,许多网络是无标度的,尽管统计分析驳斥了其中许多说法,并对其他说法提出了严重质疑。提出了优先连接和适应度模型作为解释实际网络中假设的幂律度分布的机制。
History
In studies of the networks of citations between scientific papers, Derek de Solla Price showed in 1965 that the number of links to papers—i.e., the number of citations they receive—had a heavy-tailed distribution following a Pareto distribution or power law, and thus that the citation network is scale-free. He did not however use the term "scale-free network", which was not coined until some decades later. In a later paper in 1976, Price also proposed a mechanism to explain the occurrence of power laws in citation networks, which he called "cumulative advantage" but which is today more commonly known under the name preferential attachment.
In studies of the networks of citations between scientific papers, Derek de Solla Price showed in 1965 that the number of links to papers—i.e., the number of citations they receive—had a heavy-tailed distribution following a Pareto distribution or power law, and thus that the citation network is scale-free. He did not however use the term "scale-free network", which was not coined until some decades later. In a later paper in 1976, Price also proposed a mechanism to explain the occurrence of power laws in citation networks, which he called "cumulative advantage" but which is today more commonly known under the name preferential attachment.
在对科学论文之间的引用网络的研究中,Derek de Solla Price 在1965年指出,论文链接的数量---- 也就是说,他们收到的引用数量---- 遵循重尾分布或帕累托分布,因此引用网络是无标度的。然而,他并没有使用“无尺度网络”这个词,这个词直到几十年后才被创造出来。在1976年后来的一篇论文中,普赖斯还提出了一种解释引文网络中幂律发生的机制,他称之为“累积优势” ,但现在更常用的名称是优先连接。
Recent interest in scale-free networks started in 1999 with work by Albert-László Barabási and colleagues at the University of Notre Dame who mapped the topology of a portion of the World Wide Web,引用错误:没有找到与</ref>对应的<ref>标签 finding that some nodes, which they called "hubs", had many more connections than others and that the network as a whole had a power-law distribution of the number of links connecting to a node. After finding that a few other networks, including some social and biological networks, also had heavy-tailed degree distributions, Barabási and collaborators coined the term "scale-free network" to describe the class of networks that exhibit a power-law degree distribution. However, studying seven examples of networks in social, economic, technological, biological, and physical systems, Amaral et al. were not able to find a scale-free network among these seven examples. Only one of these examples, the movie-actor network, had degree distribution P(k) following a power law regime for moderate k, though eventually this power law regime was followed by a sharp cutoff showing exponential decay for large k.[5]
|bibcode = 1999Sci...286..509B }}</ref> finding that some nodes, which they called "hubs", had many more connections than others and that the network as a whole had a power-law distribution of the number of links connecting to a node. After finding that a few other networks, including some social and biological networks, also had heavy-tailed degree distributions, Barabási and collaborators coined the term "scale-free network" to describe the class of networks that exhibit a power-law degree distribution. However, studying seven examples of networks in social, economic, technological, biological, and physical systems, Amaral et al. were not able to find a scale-free network among these seven examples. Only one of these examples, the movie-actor network, had degree distribution P(k) following a power law regime for moderate k, though eventually this power law regime was followed by a sharp cutoff showing exponential decay for large k.
1999 / sci... 286. . 509 b } / ref 发现一些节点,他们称之为“集线器” ,比其他节点有更多的连接,并且整个网络具有连接到一个节点的链接数量的幂律分布。在发现其他一些网络,包括一些社会和生物网络,也有重尾度分布之后,barab si 和合作者创造了术语“无尺度网络”来描述呈现幂律度分布的网络类型。然而,研究网络在社会、经济、技术、生物和物理系统中的七个例子,Amaral 等。我们未能在这七个例子中找到无尺度网络。只有一个例子,电影演员网络,有度分布 p (k)遵循的是中等 k 的幂律制度,尽管最终这种幂律制度紧随其后的是大 k 的指数衰减。
Barabási and Réka Albert proposed a generative mechanism to explain the appearance of power-law distributions, which they called "preferential attachment" and which is essentially the same as that proposed by Price. Analytic solutions for this mechanism (also similar to the solution of Price) were presented in 2000 by Dorogovtsev, Mendes and Samukhin [6] and independently by Krapivsky, Redner, and Leyvraz, and later rigorously proved by mathematician Béla Bollobás.[7] Notably, however, this mechanism only produces a specific subset of networks in the scale-free class, and many alternative mechanisms have been discovered since.[8]
Barabási and Réka Albert proposed a generative mechanism to explain the appearance of power-law distributions, which they called "preferential attachment" and which is essentially the same as that proposed by Price. Analytic solutions for this mechanism (also similar to the solution of Price) were presented in 2000 by Dorogovtsev, Mendes and Samukhin and independently by Krapivsky, Redner, and Leyvraz, and later rigorously proved by mathematician Béla Bollobás. Notably, however, this mechanism only produces a specific subset of networks in the scale-free class, and many alternative mechanisms have been discovered since.
巴拉布 · 西和 r · 卡 · 阿尔伯特提出了一种生成机制来解释幂律分布的出现,他们称之为“优先附加” ,这与普赖斯提出的分布在本质上是一致的。2000年,Dorogovtsev、 Mendes 和 Samukhin 分别提出了这一机制的解析解(也类似于 Price 解) ,Krapivsky、 Redner 和 Leyvraz 各自提出了解析解,后来由数学家 b la bollob 给出了严格的证明。然而,值得注意的是,这种机制只在无标度类中生成特定的网络子集,此后发现了许多替代机制。
The history of scale-free networks also includes some disagreement. On an empirical level, the scale-free nature of several networks has been called into question. For instance, the three brothers Faloutsos believed that the Internet had a power law degree distribution on the basis of traceroute data; however, it has been suggested that this is a layer 3 illusion created by routers, which appear as high-degree nodes while concealing the internal layer 2 structure of the ASes they interconnect.
The history of scale-free networks also includes some disagreement. On an empirical level, the scale-free nature of several networks has been called into question. For instance, the three brothers Faloutsos believed that the Internet had a power law degree distribution on the basis of traceroute data; however, it has been suggested that this is a layer 3 illusion created by routers, which appear as high-degree nodes while concealing the internal layer 2 structure of the ASes they interconnect.
无标度网络的历史也包含一些分歧。在经验层面上,几个网络的无标度性质已经受到质疑。例如,法鲁特索斯三兄弟认为,互联网有一个幂律度分布的追踪数据的基础上,但有人提出,这是一个第三层幻想,由路由器创造,这似乎是高度节点,同时掩盖了内部的第二层结构,他们互连。
引用错误:没有找到与</ref>对应的<ref>标签
</ref>
/ 参考
On a theoretical level, refinements to the abstract definition of scale-free have been proposed. For example, Li et al. (2005) recently offered a potentially more precise "scale-free metric". Briefly, let G be a graph with edge set E, and denote the degree of a vertex [math]\displaystyle{ v }[/math] (that is, the number of edges incident to [math]\displaystyle{ v }[/math]) by [math]\displaystyle{ \deg(v) }[/math]. Define
On a theoretical level, refinements to the abstract definition of scale-free have been proposed. For example, Li et al. (2005) recently offered a potentially more precise "scale-free metric". Briefly, let G be a graph with edge set E, and denote the degree of a vertex [math]\displaystyle{ v }[/math] (that is, the number of edges incident to [math]\displaystyle{ v }[/math]) by [math]\displaystyle{ \deg(v) }[/math]. Define
在理论层面上,对无标度抽象定义进行了改进。例如,李等人。(2005年)最近提出了一个可能更为精确的“无标度度量”。简单地说,设 g 是一个具有边集 e 的图,用 math deg (v) / math 表示顶点数学 v / math 的度数(即与 math v / math 相关的边数)。定义
- [math]\displaystyle{ s(G) = \sum_{(u,v) \in E} \deg(u) \cdot \deg(v). }[/math]
[math]\displaystyle{ s(G) = \sum_{(u,v) \in E} \deg(u) \cdot \deg(v). }[/math]
Math s (g) sum {(u,v) in e } deg (u) cdot deg (v) . / math
This is maximized when high-degree nodes are connected to other high-degree nodes. Now define
This is maximized when high-degree nodes are connected to other high-degree nodes. Now define
当高度节点连接到其他高度节点时,这个值最大化。现在定义一下
- [math]\displaystyle{ S(G) = \frac{s(G)}{s_\max}, }[/math]
[math]\displaystyle{ S(G) = \frac{s(G)}{s_\max}, }[/math]
数学 s (g) frac { s (g)} s max,/ math
where smax is the maximum value of s(H) for H in the set of all graphs with degree distribution identical to that of G. This gives a metric between 0 and 1, where a graph G with small S(G) is "scale-rich", and a graph G with S(G) close to 1 is "scale-free". This definition captures the notion of self-similarity implied in the name "scale-free".
where smax is the maximum value of s(H) for H in the set of all graphs with degree distribution identical to that of G. This gives a metric between 0 and 1, where a graph G with small S(G) is "scale-rich", and a graph G with S(G) close to 1 is "scale-free". This definition captures the notion of self-similarity implied in the name "scale-free".
其中 s 次 max / sub 是所有度分布与 g 完全相同的图集中 h 的 s (h)的最大值。 这给出了一个介于0和1之间的度量,其中小 s (g)的图 g 是“刻度丰富的” ,而 s (g)接近1的图 g 是“无刻度的”。这个定义抓住了“无标度”这个名称所隐含的自相似性的概念。
Overview
There are two major components that explain the emergence of the scale-free property in a complex networks: the growth and the preferential attachment.引用错误:没有找到与</ref>对应的<ref>标签
}}</ref>
{} / ref
By "growth" is called a growth process where, over an extended period of time, new nodes join an already existing system, a network (like the World Wide Web which has grown by billions of web pages over 10 years).
By "growth" is called a growth process where, over an extended period of time, new nodes join an already existing system, a network (like the World Wide Web which has grown by billions of web pages over 10 years).
通过“增长”被称为一个增长过程,在一个延长的时期内,新的节点加入一个已经存在的系统,一个网络(就像万维网,在过去10年里增长了数十亿个网页)。
Finally, by "preferential attachment" is called a new coming node who prefers to connect to another node which has already a certain number of links with others. Thus, there is a higher probability that more and more nodes will link themselves to that one which has already many links, leading this node to a hub in-fine.[9]
Finally, by "preferential attachment" is called a new coming node who prefers to connect to another node which has already a certain number of links with others. Thus, there is a higher probability that more and more nodes will link themselves to that one which has already many links, leading this node to a hub in-fine.
最后,通过“优先连接”被称为新的未来节点,它更愿意连接到另一个已经与其他节点有一定数量链接的节点。因此,越来越多的节点将自己链接到那个已经有很多链接的节点的可能性越来越大,这使得这个节点最终链接到一个中心。
Depending on the network, the hubs might either be assortative or disassortative. Assortativity would be found in social networks in which well-connected/famous people would tend to know better each other. Disassortativity would be found in technological (Internet, World Wide Web) and biological (protein interaction, metabolism) networks.[10]
Depending on the network, the hubs might either be assortative or disassortative. Assortativity would be found in social networks in which well-connected/famous people would tend to know better each other. Disassortativity would be found in technological (Internet, World Wide Web) and biological (protein interaction, metabolism) networks.
根据网络的不同,集线器可能是选型的,也可能是反选型的。在社交网络中可以发现相称性,在这种社交网络中,关系密切的名人往往更加了解彼此。在技术(互联网、万维网)和生物(蛋白质相互作用、代谢)网络中可以发现不协调性。
Characteristics
Random network (a) and scale-free network (b). In the scale-free network, the larger hubs are highlighted.
随机网络(a)和无尺度网络(b)。在无尺度网络中,较大的枢纽被突出显示。
Complex network degree distribution of random and scale-free
随机无标度的复杂网络度分布
The most notable characteristic in a scale-free network is the relative commonness of vertices with a degree that greatly exceeds the average. The highest-degree nodes are often called "hubs", and are thought to serve specific purposes in their networks, although this depends greatly on the domain.
The most notable characteristic in a scale-free network is the relative commonness of vertices with a degree that greatly exceeds the average. The highest-degree nodes are often called "hubs", and are thought to serve specific purposes in their networks, although this depends greatly on the domain.
无尺度网络最显著的特征是顶点的相对共性,这些顶点的度大大超过了平均值。最高度的节点通常被称为“集线器” ,并被认为在其网络中服务于特定的目的,尽管这在很大程度上取决于领域。
Percolation
The scale-free property strongly correlates with the network's robustness to failure. It turns out that the major hubs are closely followed by smaller ones. These smaller hubs, in turn, are followed by other nodes with an even smaller degree and so on. This hierarchy allows for a fault tolerant behavior. If failures occur at random and the vast majority of nodes are those with small degree, the likelihood that a hub would be affected is almost negligible. Even if a hub-failure occurs, the network will generally not lose its connectedness, due to the remaining hubs. On the other hand, if we choose a few major hubs and take them out of the network, the network is turned into a set of rather isolated graphs. Thus, hubs are both a strength and a weakness of scale-free networks. These properties have been studied analytically using percolation theory by Cohen et al.引用错误:没有找到与</ref>对应的<ref>标签[11] and by Callaway et al.[12] It was proven by Cohen et al [13] that for a broad range of scale free networks, for [math]\displaystyle{ 2 \lt \gamma \lt 3 }[/math] the critical percolation threshold,模板:Space[math]\displaystyle{ p_c=0 }[/math]. This means that removing randomly any fraction of nodes from the network will not destroy the network. This is in contrast to Erdős–Rényi graph where [math]\displaystyle{ p_c =1/\bar{k} }[/math], where [math]\displaystyle{ \bar{k} }[/math] is the average degree. The failures discussed above are random, as usually assumed in percolation theory. However, when generalizing percolation also to non-random but targeted attacks, e.g., on highest degree nodes, the results, such as p_c, change significantly.[11][12]
volume=85|issue=21|pages=4626–8|doi= 10.1103/PhysRevLett.85.4626|bibcode=2000PhRvL..85.4626C|arxiv = cond-mat/0007048 |pmid=11082612}}</ref> and by Callaway et al. It was proven by Cohen et al that for a broad range of scale free networks, for [math]\displaystyle{ 2 \lt \gamma \lt 3 }[/math] the critical percolation threshold,[math]\displaystyle{ p_c=0 }[/math]. This means that removing randomly any fraction of nodes from the network will not destroy the network. This is in contrast to Erdős–Rényi graph where [math]\displaystyle{ p_c =1/\bar{k} }[/math], where [math]\displaystyle{ \bar{k} }[/math] is the average degree. The failures discussed above are random, as usually assumed in percolation theory. However, when generalizing percolation also to non-random but targeted attacks, e.g., on highest degree nodes, the results, such as p_c, change significantly.
85 | issue 21 | pages 4626-8 | doi 10.1103 / physrvlett. 85.4626 | bibcode 2000PhRvL. . 85.4626 c | arxiv cond-mat / 0007048 | pmd 11082612} / ref et al. .Cohen 等人证明了对于广泛的无标度网络,对于数学2 γ3 / math 临界渗流阈值,即数学 pc0 / math。这意味着从网络中随机移除任何节点都不会破坏网络。这与 Erdős-r nyi 图形成对比,在那里 math p c 1 / bar { k } / math 是平均度。正如逾渗理论中通常假设的那样,上面讨论的失效是随机的。然而,当渗透推广到非随机但有针对性的攻击时,例如对最高度节点的攻击,其结果,例如 p c,会发生显著的变化。
Recently, a new type of failures in networks has been developed, called localized attacks[14]. In this case one choses randomly a node and remove its neighbors and next nearest neighbors until a fraction of 1-p nodes are removed
Recently, a new type of failures in networks has been developed, called localized attacks. In this case one choses randomly a node and remove its neighbors and next nearest neighbors until a fraction of 1-p nodes are removed
近年来,出现了一种新的网络故障类型,称为局部攻击。在这种情况下,一个随机选择一个节点,并删除它的邻居和次近邻,直到1-p 节点的一小部分被删除
Another important characteristic of scale-free networks is the clustering coefficient distribution, which decreases as the node degree increases. This distribution also follows a power law. This implies that the low-degree nodes belong to very dense sub-graphs and those sub-graphs are connected to each other through hubs. Consider a social network in which nodes are people and links are acquaintance relationships between people. It is easy to see that people tend to form communities, i.e., small groups in which everyone knows everyone (one can think of such community as a complete graph). In addition, the members of a community also have a few acquaintance relationships to people outside that community. Some people, however, are connected to a large number of communities (e.g., celebrities, politicians). Those people may be considered the hubs responsible for the small-world phenomenon.
Another important characteristic of scale-free networks is the clustering coefficient distribution, which decreases as the node degree increases. This distribution also follows a power law. This implies that the low-degree nodes belong to very dense sub-graphs and those sub-graphs are connected to each other through hubs. Consider a social network in which nodes are people and links are acquaintance relationships between people. It is easy to see that people tend to form communities, i.e., small groups in which everyone knows everyone (one can think of such community as a complete graph). In addition, the members of a community also have a few acquaintance relationships to people outside that community. Some people, however, are connected to a large number of communities (e.g., celebrities, politicians). Those people may be considered the hubs responsible for the small-world phenomenon.
无标度网络的另一个重要特征是集聚系数分布,它随着节点度的增加而减少。这个分布也遵循一个幂定律。这意味着低度节点属于非常稠密的子图,这些子图通过集线器相互连接。考虑一个社会网络,其中的节点是人,链接是人与人之间的熟人关系。很容易看出,人们倾向于形成社区,即每个人都认识每个人的小团体(你可以把这样的社区想象成一个完整的图表)。此外,一个社区的成员与社区外的人也有一些熟人关系。然而,有些人与许多社区有联系(例如,名人、政治家)。这些人可能被认为是造成小世界现象的中心。
At present, the more specific characteristics of scale-free networks vary with the generative mechanism used to create them. For instance, networks generated by preferential attachment typically place the high-degree vertices in the middle of the network, connecting them together to form a core, with progressively lower-degree nodes making up the regions between the core and the periphery. The random removal of even a large fraction of vertices impacts the overall connectedness of the network very little, suggesting that such topologies could be useful for security, while targeted attacks destroys the connectedness very quickly. Other scale-free networks, which place the high-degree vertices at the periphery, do not exhibit these properties. Similarly, the clustering coefficient of scale-free networks can vary significantly depending on other topological details.
At present, the more specific characteristics of scale-free networks vary with the generative mechanism used to create them. For instance, networks generated by preferential attachment typically place the high-degree vertices in the middle of the network, connecting them together to form a core, with progressively lower-degree nodes making up the regions between the core and the periphery. The random removal of even a large fraction of vertices impacts the overall connectedness of the network very little, suggesting that such topologies could be useful for security, while targeted attacks destroys the connectedness very quickly. Other scale-free networks, which place the high-degree vertices at the periphery, do not exhibit these properties. Similarly, the clustering coefficient of scale-free networks can vary significantly depending on other topological details.
目前,无标度网络更具体的特征随创建无标度网络的生成机制而变化。例如,由优先连接产生的网络通常将高度的顶点放置在网络的中部,将它们连接在一起形成一个核心,核心和外围之间的区域由逐渐降低的度的节点组成。即使是很大一部分顶点的随机删除对网络的整体连接性影响很小,这表明这种拓扑可能对安全有用,而目标攻击会很快破坏连接性。其他无标度网络,把高度顶点放在周边,不表现出这些性质。类似地,无标度网络的集聚系数可以根据其他拓扑细节而发生显著的变化。
Distance in scale free networks
A further characteristic concerns the average distance between two vertices in a network. As with most disordered networks, such as the small world network model, this distance is very small relative to a highly ordered network such as a lattice graph. Notably, an uncorrelated power-law graph having 2 < γ < 3 will have ultrasmall diameter d ~ ln ln N where N is the number of nodes in the network, as proved by Cohen and Havlin.[15] Thus, the diameter of a growing scale-free network might be considered almost constant in practice.
A further characteristic concerns the average distance between two vertices in a network. As with most disordered networks, such as the small world network model, this distance is very small relative to a highly ordered network such as a lattice graph. Notably, an uncorrelated power-law graph having 2 < γ < 3 will have ultrasmall diameter d ~ ln ln N where N is the number of nodes in the network, as proved by Cohen and Havlin. Thus, the diameter of a growing scale-free network might be considered almost constant in practice.
另一个特征涉及到网络中两个顶点之间的平均距离。与大多数无序网络(如小世界网络模型)一样,这个距离相对于高度有序的网络(如格子图)来说非常小。值得注意的是,一个具有23的不相关幂律图将具有超小直径 d ~ ln n,其中 n 是网络中的节点数,正如 Cohen 和 Havlin 所证明的那样。因此,生长中的无尺度网络的直径在实践中可能被认为几乎是恒定的。
Immunization
The question of how to immunize efficiently scale free networks which represent realistic networks such as the Internet and social networks has been studied extensively. One such strategy is to immunize the largest degree nodes, i.e., targeted (intentional) attacks[16][11] since for this case p_c is relatively high and less nodes are needed to be immunized.
The question of how to immunize efficiently scale free networks which represent realistic networks such as the Internet and social networks has been studied extensively. One such strategy is to immunize the largest degree nodes, i.e., targeted (intentional) attacks since for this case p_c is relatively high and less nodes are needed to be immunized.
如何对代表现实网络如互联网和社会网络的无标度网络进行有效的免疫问题已经得到了广泛的研究。其中一种策略是免疫最大度节点,即有针对性的(有意的)攻击,因为在这种情况下,pc 相对较高,需要免疫的节点较少。
However, in most realistic nodes the global structure is not available and the largest degree nodes are not known.
However, in most realistic nodes the global structure is not available and the largest degree nodes are not known.
然而,在大多数现实节点中,全局结构是不可用的,最大度节点是不知道的。
For this case the method of acquaintance immunization has been developed[17]. In this case, which is quite efficient one choses randomly nodes but immunize their neighbors.
For this case the method of acquaintance immunization has been developed. In this case, which is quite efficient one choses randomly nodes but immunize their neighbors.
在这种情况下,熟人免疫方法已经发展起来。在这种情况下,这是相当有效的一个选择随机节点,但免疫他们的邻居。
Another and even more efficient method is based on graph parition method [18] .
Another and even more efficient method is based on graph parition method .
另一种更有效的方法是基于图分解的方法。
Properties of random graph may change or remain invariant under graph transformations. Mashaghi A. et al., for example, demonstrated that a transformation which converts random graphs to their edge-dual graphs (or line graphs) produces an ensemble of graphs with nearly the same degree distribution, but with degree correlations and a significantly higher clustering coefficient. Scale free graphs, as such, remain scale free under such transformations.[19]
Properties of random graph may change or remain invariant under graph transformations. Mashaghi A. et al., for example, demonstrated that a transformation which converts random graphs to their edge-dual graphs (or line graphs) produces an ensemble of graphs with nearly the same degree distribution, but with degree correlations and a significantly higher clustering coefficient. Scale free graphs, as such, remain scale free under such transformations.
随机图的性质在图变换下可以改变或保持不变。例如,Mashaghi a. et A.. 证明了将随机图转换为边-对偶图(或线图)的转换产生了一个几乎具有相同程度分布的图的集合,但是具有程度相关性和一个明显更高的集聚系数。无标度图本身在这种变换下仍然是无标度的。
Examples
Although many real-world networks are thought to be scale-free, the evidence often remains inconclusive, primarily due to the developing awareness of more rigorous data analysis techniques.[3] As such, the scale-free nature of many networks is still being debated by the scientific community. A few examples of networks claimed to be scale-free include:
Although many real-world networks are thought to be scale-free, the evidence often remains inconclusive, primarily due to the developing awareness of more rigorous data analysis techniques. As such, the scale-free nature of many networks is still being debated by the scientific community. A few examples of networks claimed to be scale-free include:
尽管许多现实世界的网络被认为是无标度的,但证据往往仍然不确定,主要是由于对更严格的数据分析技术的认识不断发展。因此,许多网络的无标度性质仍在科学界争论不休。一些声称是无标度网络的例子包括:
- Some Social networks, including collaboration networks. Two examples that have been studied extensively are the collaboration of movie actors in films and the co-authorship by mathematicians of papers.
- Many kinds of computer networks, including the internet and the webgraph of the World Wide Web.
- Protein-protein interaction networks.
- Airline networks.
A snapshot of the weighted planar stochastic lattice (WPSL).
加权平面随机晶格的一个快照。
Scale free topology has been also found in high temperature superconductors.[25] The qualities of a high-temperature superconductor — a compound in which electrons obey the laws of quantum physics, and flow in perfect synchrony, without friction — appear linked to the fractal arrangements of seemingly random oxygen atoms and lattice distortion.[26]
Scale free topology has been also found in high temperature superconductors. The qualities of a high-temperature superconductor — a compound in which electrons obey the laws of quantum physics, and flow in perfect synchrony, without friction — appear linked to the fractal arrangements of seemingly random oxygen atoms and lattice distortion.
在高温超导体中也发现了无标度拓扑结构。高温超导体——一种电子遵循量子物理定律,完全同步流动,没有摩擦的化合物——的性质似乎与看似随机的氧原子的分形排列和晶格畸变有关。
A space-filling cellular structure, weighted planar stochastic lattice (WPSL) has recently been proposed whose coordination number distribution follow a power-law. It implies that the lattice has a few blocks which have astonishingly large number neighbors with whom they share common borders. Its construction starts with an initiator, say a
A space-filling cellular structure, weighted planar stochastic lattice (WPSL) has recently been proposed whose coordination number distribution follow a power-law. It implies that the lattice has a few blocks which have astonishingly large number neighbors with whom they share common borders. Its construction starts with an initiator, say a
最近提出了一种填充空间的网格结构——加权平面随机格(WPSL) ,其配位数分布服从幂律。这意味着格子有几个块,它们有着数量惊人的邻居,它们共享相同的边界。它的构造始于一个发起者,比如一个
square of unit area, and a generator that divides it randomly into four blocks. The generator thereafter is sequentially applied
square of unit area, and a generator that divides it randomly into four blocks. The generator thereafter is sequentially applied
单位面积的平方,以及一个随机分成四个街区的发电机。此后将顺序应用生成器
over and over again to only one of the available blocks picked preferentially with respect to their areas. It results in the partitioning of the square into ever smaller mutually exclusive rectangular blocks. The dual of the WPSL (DWPSL) is obtained by replacing each block with a node at its center and common border
over and over again to only one of the available blocks picked preferentially with respect to their areas. It results in the partitioning of the square into ever smaller mutually exclusive rectangular blocks. The dual of the WPSL (DWPSL) is obtained by replacing each block with a node at its center and common border
一遍又一遍,只有一个可用的块优先采摘相对于他们的地区。它的结果是将正方形分割成更小的相互排斥的矩形块。Wpsl (DWPSL)的对偶是通过在每个块的中心和公共边界上放置一个节点来获得的
between blocks with an edge joining the two corresponding vertices emerges as a network whose degree distribution follows
between blocks with an edge joining the two corresponding vertices emerges as a network whose degree distribution follows
边连接两个相应顶点的块之间形成一个度分布如下的网络
a power-law.[27][28] The reason for it is that it grows following mediation-driven attachment model rule which also embodies preferential attachment rule but in disguise.
a power-law. The reason for it is that it grows following mediation-driven attachment model rule which also embodies preferential attachment rule but in disguise.
幂律。究其原因,是因为它是遵循中介驱动的依恋模型规则发展起来的,这种模型规则也体现了优先依恋规则,但是是伪装的。
Generative models
Scale-free networks do not arise by chance alone. Erdős and Rényi (1960) studied a model of growth for graphs in which, at each step, two nodes are chosen uniformly at random and a link is inserted between them. The properties of these random graphs are different from the properties found in scale-free networks, and therefore a model for this growth process is needed.
Scale-free networks do not arise by chance alone. Erdős and Rényi (1960) studied a model of growth for graphs in which, at each step, two nodes are chosen uniformly at random and a link is inserted between them. The properties of these random graphs are different from the properties found in scale-free networks, and therefore a model for this growth process is needed.
无标度网络不是偶然出现的。Erd s 和 rnyi (1960)研究了图的增长模型,其中每一步均匀地随机选择两个节点,并在它们之间插入一个链路。这些随机图的性质不同于无标度网络的性质,因此需要一个模型来描述这种增长过程。
The most widely known generative model for a subset of scale-free networks is Barabási and Albert's (1999) rich get richer generative model in which each new Web page creates links to existing Web pages with a probability distribution which is not uniform, but
The most widely known generative model for a subset of scale-free networks is Barabási and Albert's (1999) rich get richer generative model in which each new Web page creates links to existing Web pages with a probability distribution which is not uniform, but
无标度网络子集中最广为人知的生成模型是 barab si 和 Albert (1999)的 rich get richer 生成模型,其中每个新网页创建到现有网页的链接,其概率分布不是统一的,而是
proportional to the current in-degree of Web pages. This model was originally invented by Derek J. de Solla Price in 1965 under the term cumulative advantage, but did not reach popularity until Barabási rediscovered the results under its current name (BA Model). According to this process, a page with many in-links will attract more in-links than a regular page. This generates a power-law but the resulting graph differs from the actual Web graph in other properties such as the presence of small tightly connected communities. More general models and network characteristics have been proposed and studied. For example, Pachon et al. (2018) proposed a variant of the rich get richer generative model which takes into account two different attachment rules: a preferential attachment mechanism and a uniform choice only for the most recent nodes.[29] For a review see the book by Dorogovtsev and Mendes.
proportional to the current in-degree of Web pages. This model was originally invented by Derek J. de Solla Price in 1965 under the term cumulative advantage, but did not reach popularity until Barabási rediscovered the results under its current name (BA Model). According to this process, a page with many in-links will attract more in-links than a regular page. This generates a power-law but the resulting graph differs from the actual Web graph in other properties such as the presence of small tightly connected communities. More general models and network characteristics have been proposed and studied. For example, Pachon et al. (2018) proposed a variant of the rich get richer generative model which takes into account two different attachment rules: a preferential attachment mechanism and a uniform choice only for the most recent nodes. For a review see the book by Dorogovtsev and Mendes.
与当前 Web 页面的 in 度成正比。这个模型最初是由德瑞克·约翰·德索拉·普莱斯在1965年发明的术语累积优势,但没有达到普及,直到 barab si 重新发现的结果在其现在的名称(BA 模型)。根据这个过程,一个有很多链接的页面会比一个普通页面吸引更多的链接。这会产生一个幂定律,但是得到的图与实际的网络图在其他属性上有所不同,比如小型紧密连接的社区的存在。提出并研究了更一般的模型和网络特性。例如,Pachon 等人。(2018)提出了一种富人变得更富有的生成模型,它考虑了两种不同的连接规则: 优先连接机制和仅针对最近的节点的统一选择。有关评论,请参阅 Dorogovtsev 和 Mendes 的书。
A somewhat different generative model for Web links has been suggested by Pennock et al. (2002). They examined communities with interests in a specific topic such as the home pages of universities, public companies, newspapers or scientists, and discarded the major hubs of the Web. In this case, the distribution of links was no longer a power law but resembled a normal distribution. Based on these observations, the authors proposed a generative model that mixes preferential attachment with a baseline probability of gaining a link.
A somewhat different generative model for Web links has been suggested by Pennock et al. (2002). They examined communities with interests in a specific topic such as the home pages of universities, public companies, newspapers or scientists, and discarded the major hubs of the Web. In this case, the distribution of links was no longer a power law but resembled a normal distribution. Based on these observations, the authors proposed a generative model that mixes preferential attachment with a baseline probability of gaining a link.
等人提出了一个略有不同的网络链接生成模型。(2002).他们调查了那些对某个特定主题感兴趣的社区,比如大学、上市公司、报纸或科学家的主页,然后放弃了主要的网络中心。在这种情况下,链节的分布不再是幂律,而是类似于正态分布。基于这些观察,作者们提出了一种混合了优先连接和获得连接的基线概率的生成模型。
Another generative model is the copy model studied by Kumar et al.[30] (2000),
Another generative model is the copy model studied by Kumar et al. (2000),
另一个生成模型是 Kumar 等人研究的复制模型。(2000),
in which new nodes choose an existent node at random and copy a fraction of the links of the existent node. This also generates a power law.
in which new nodes choose an existent node at random and copy a fraction of the links of the existent node. This also generates a power law.
其中新的节点随机选择存在的节点并复制存在节点的链路的一部分。这也产生了一个幂定律。
The growth of the networks (adding new nodes) is not a necessary condition for creating a scale-free network. Dangalchev[31] (2004) gives examples of generating static scale-free networks. Another possibility (Caldarelli et al. 2002) is to consider the structure as static and draw a link between vertices according to a particular property of the two vertices involved. Once specified the statistical distribution for these vertex properties (fitnesses), it turns out that in some circumstances also static networks develop scale-free properties.
The growth of the networks (adding new nodes) is not a necessary condition for creating a scale-free network. Dangalchev (2004) gives examples of generating static scale-free networks. Another possibility (Caldarelli et al. 2002) is to consider the structure as static and draw a link between vertices according to a particular property of the two vertices involved. Once specified the statistical distribution for these vertex properties (fitnesses), it turns out that in some circumstances also static networks develop scale-free properties.
网络的增长(增加新的节点)并不是创建无尺度网络的必要条件。Dangalchev (2004)给出了生成静态无标度网络的例子。另一种可能性(Caldarelli et al. 。2002)是考虑结构为静态和绘制之间的顶点根据特定性质的两个顶点参与。一旦确定了这些顶点属性(fitness)的统计分布,就会发现在某些情况下,静态网络也会发展出无标度属性。
Generalized scale-free model
There has been a burst of activity in the modeling of scale-free complex networks. The recipe of Barabási and Albert[32] has been followed by several variations and generalizations[33][34][35][36][29] and the revamping of previous mathematical works.[37] As long as there is a power law distribution in a model, it is a scale-free network, and a model of that network is a scale-free model.
There has been a burst of activity in the modeling of scale-free complex networks. The recipe of Barabási and Albert has been followed by several variations and generalizations and the revamping of previous mathematical works. As long as there is a power law distribution in a model, it is a scale-free network, and a model of that network is a scale-free model.
在无标度复杂网络的建模中,出现了大量的活动。Barabási 和阿尔伯特的秘方之后,又出现了一些变化和概括,并对以前的数学作品进行了改造。只要一个模型中存在幂律分布,那么它就是一个无尺度网络,而该网络的模型就是一个无标度模型。
Features
Many real networks are (approximately) scale-free and hence require scale-free models to describe them. In Price's scheme, there are two ingredients needed to build up a scale-free model:
Many real networks are (approximately) scale-free and hence require scale-free models to describe them. In Price's scheme, there are two ingredients needed to build up a scale-free model:
许多真实的网络是近似无标度的,因此需要无标度模型来描述它们。在普莱斯的方案中,建立无标度模型需要两个要素:
1. Adding or removing nodes. Usually we concentrate on growing the network, i.e. adding nodes.
1. Adding or removing nodes. Usually we concentrate on growing the network, i.e. adding nodes.
1.添加或移除节点。通常我们集中精力扩大网络,例如。加法节点。
2. Preferential attachment: The probability [math]\displaystyle{ \Pi }[/math] that new nodes will be connected to the "old" node.
2. Preferential attachment: The probability [math]\displaystyle{ \Pi }[/math] that new nodes will be connected to the "old" node.
2.优先连接: 新节点将连接到“旧”节点的概率数学 Pi / math。
Note that Fitness models (see below) could work also statically, without changing the number of nodes. It should also be kept in mind that the fact that "preferential attachment" models give rise to scale-free networks does not prove that this is the mechanism underlying the evolution of real-world scale-free networks, as there might exist different mechanisms at work in real-world systems that nevertheless give rise to scaling.
Note that Fitness models (see below) could work also statically, without changing the number of nodes. It should also be kept in mind that the fact that "preferential attachment" models give rise to scale-free networks does not prove that this is the mechanism underlying the evolution of real-world scale-free networks, as there might exist different mechanisms at work in real-world systems that nevertheless give rise to scaling.
请注意,Fitness 模型(见下文)也可以静态地工作,而不改变节点的数量。还应当铭记,”优先连接”模型产生无标度网络这一事实并不能证明这是现实世界无标度网络演变的基本机制,因为在现实世界系统中可能存在不同的机制,但这些机制会引起扩展。
Examples
There have been several attempts to generate scale-free network properties. Here are some examples:
There have been several attempts to generate scale-free network properties. Here are some examples:
已经有几次尝试生成无尺度网络的属性。以下是一些例子:
The Barabási–Albert model
For example, the first scale-free model, the Barabási–Albert model, has a linear preferential attachment [math]\displaystyle{ \Pi(k_i)=\frac{k_i}{\sum_j k_j} }[/math] and adds one new node at every time step.
For example, the first scale-free model, the Barabási–Albert model, has a linear preferential attachment [math]\displaystyle{ \Pi(k_i)=\frac{k_i}{\sum_j k_j} }[/math] and adds one new node at every time step.
例如,第一个无标度模型 barab si-Albert 模型具有线性优先连接数学 Pi (ki) frac { ki }{ j k } / math,并且在每个时间步增加一个新节点。
(Note, another general feature of [math]\displaystyle{ \Pi(k) }[/math] in real networks is that [math]\displaystyle{ \Pi(0)\neq 0 }[/math], i.e. there is a nonzero probability that a
(Note, another general feature of [math]\displaystyle{ \Pi(k) }[/math] in real networks is that [math]\displaystyle{ \Pi(0)\neq 0 }[/math], i.e. there is a nonzero probability that a
(注意,实际网络中 math Pi (k) / math 的另一个普遍特性是 math Pi (0) neq 0 / math,即。有一个非零的概率
new node attaches to an isolated node. Thus in general [math]\displaystyle{ \Pi(k) }[/math] has the form [math]\displaystyle{ \Pi(k)=A +k^\alpha }[/math], where [math]\displaystyle{ A }[/math] is the initial attractiveness of the node.)
new node attaches to an isolated node. Thus in general [math]\displaystyle{ \Pi(k) }[/math] has the form [math]\displaystyle{ \Pi(k)=A +k^\alpha }[/math], where [math]\displaystyle{ A }[/math] is the initial attractiveness of the node.)
新节点连接到一个独立的节点。因此,在一般的 math Pi (k) / math 中,形式是 math Pi (k) a + k ^ alpha / math,其中 math a / math 是节点的初始吸引力
Two-level network model
Dangalchev[31] builds a 2-L model by adding a second-order preferential attachment. The attractiveness of a node in the 2-L model depends not only on the number of nodes linked to it but also on the number of links in each of these nodes.
Dangalchev builds a 2-L model by adding a second-order preferential attachment. The attractiveness of a node in the 2-L model depends not only on the number of nodes linked to it but also on the number of links in each of these nodes.
Dangalchev 通过增加一个二阶优先连接,建立了一个2-L 模型。在2-L 模型中,一个节点的吸引力不仅取决于链接到它的节点数量,还取决于每个节点中链接的数量。
- [math]\displaystyle{ \Pi(k_i)=\frac{k_i + C \sum_{(i,j)} k_j}{\sum_j k_j + C \sum_j k_j^2}, }[/math]
[math]\displaystyle{ \Pi(k_i)=\frac{k_i + C \sum_{(i,j)} k_j}{\sum_j k_j + C \sum_j k_j^2}, }[/math]
数学 Pi (ki) frac { k i + c sum {(i,j)}{ sum j j + c sum j j ^ 2} ,/ math
where C is a coefficient between 0 and 1.
where C is a coefficient between 0 and 1.
其中 c 的系数介于0和1之间。
Mediation-driven attachment (MDA) model
In the mediation-driven attachment (MDA) model, a new node coming with [math]\displaystyle{ m }[/math] edges picks an existing connected node at random and then connects itself, not with that one, but with [math]\displaystyle{ m }[/math] of its neighbors, also chosen at random. The probability [math]\displaystyle{ \Pi(i) }[/math] that the node [math]\displaystyle{ i }[/math] of the existing node picked is
In the mediation-driven attachment (MDA) model, a new node coming with [math]\displaystyle{ m }[/math] edges picks an existing connected node at random and then connects itself, not with that one, but with [math]\displaystyle{ m }[/math] of its neighbors, also chosen at random. The probability [math]\displaystyle{ \Pi(i) }[/math] that the node [math]\displaystyle{ i }[/math] of the existing node picked is
在中介驱动依恋(mediation-driven attachment,MDA)模型中,一个带有数学 m / math 边的新节点随机选择一个现有的连接节点,然后与它自己连接,不是与那个节点,而是与它的邻居的数学 m / math,也是随机选择的。所选节点的节点 math i / math 是概率数学 Pi (i) / math
- [math]\displaystyle{ \Pi(i) = \frac{k_i} N \frac{\sum_{j=1}^{k_i} \frac 1 {k_j} }{k_i}. }[/math]
[math]\displaystyle{ \Pi(i) = \frac{k_i} N \frac{\sum_{j=1}^{k_i} \frac 1 {k_j} }{k_i}. }[/math]
数学 Pi (i) frac { k i } n frac { j 1} ^ { k i } frac 1{ k i } . / math
The factor [math]\displaystyle{ \frac{\sum_{j=1}^{k_i} \frac 1 {k_j} }{k_i} }[/math] is the inverse of the harmonic mean
The factor [math]\displaystyle{ \frac{\sum_{j=1}^{k_i} \frac 1 {k_j} }{k_i} }[/math] is the inverse of the harmonic mean
因子 math frac { j 1} ^ { k i } frac 1{ k j }{ k i } / math 是调和平均数的逆
(IHM) of degrees of the [math]\displaystyle{ k_i }[/math] neighbors of a node [math]\displaystyle{ i }[/math]. Extensive numerical investigation suggest that for approximately [math]\displaystyle{ m\gt 14 }[/math] the mean IHM value in the large [math]\displaystyle{ N }[/math] limit becomes a constant which means [math]\displaystyle{ \Pi(i) \propto k_i }[/math]. It implies that the higher the
(IHM) of degrees of the [math]\displaystyle{ k_i }[/math] neighbors of a node [math]\displaystyle{ i }[/math]. Extensive numerical investigation suggest that for approximately [math]\displaystyle{ m\gt 14 }[/math] the mean IHM value in the large [math]\displaystyle{ N }[/math] limit becomes a constant which means [math]\displaystyle{ \Pi(i) \propto k_i }[/math]. It implies that the higher the
数学知识的度数 / 数学邻居的节点数学知识 / 数学。大量的数值研究表明,对于近似的数学 m14 / math,大数学 n / math 极限的平均 IHM 值变成了一个常数,这意味着数学 Pi (i) / propto k i / math。这意味着
links (degree) a node has, the higher its chance of gaining more links since they can be
links (degree) a node has, the higher its chance of gaining more links since they can be
一个节点拥有的链接(度)越多,它获得更多链接的机会就越高,因为它们可以
reached in a larger number of ways through mediators which essentially embodies the intuitive
reached in a larger number of ways through mediators which essentially embodies the intuitive
通过中介器达到更多的方式,这本质上体现了直观的
idea of rich get richer mechanism (or the preferential attachment rule of the Barabasi–Albert model). Therefore, the MDA network can be seen to follow
idea of rich get richer mechanism (or the preferential attachment rule of the Barabasi–Albert model). Therefore, the MDA network can be seen to follow
富人变得更富有的机制(或者是 Barabasi-Albert 模型的优先依附规则)。因此,MDA 网络可以被看作是后续的
the PA rule but in disguise.[38]
the PA rule but in disguise.
巴勒斯坦权力机构的规则,但是是伪装的。
However, for [math]\displaystyle{ m=1 }[/math] it describes the winner takes it all mechanism as we find that almost [math]\displaystyle{ 99\% }[/math] of the total nodes has degree one and one is super-rich in degree. As [math]\displaystyle{ m }[/math] value increases the disparity between the super rich and poor decreases and as [math]\displaystyle{ m\gt 14 }[/math] we find a transition from rich get super richer to rich get richer mechanism.
However, for [math]\displaystyle{ m=1 }[/math] it describes the winner takes it all mechanism as we find that almost [math]\displaystyle{ 99\% }[/math] of the total nodes has degree one and one is super-rich in degree. As [math]\displaystyle{ m }[/math] value increases the disparity between the super rich and poor decreases and as [math]\displaystyle{ m\gt 14 }[/math] we find a transition from rich get super richer to rich get richer mechanism.
然而,对于数学 m1 / math,它描述了赢家通吃的机制,因为我们发现几乎所有节点的数学99 / math 都是度1,度1是超级丰富的。数学价值增加了超级富人和穷人之间的差距,数学价值增加了超级富人和穷人之间的差距,我们发现了从富人变得超级富人到富人变得更富有的机制。
Non-linear preferential attachment
The Barabási–Albert model assumes that the probability [math]\displaystyle{ \Pi(k) }[/math] that a node attaches to node [math]\displaystyle{ i }[/math] is proportional to the degree [math]\displaystyle{ k }[/math] of node [math]\displaystyle{ i }[/math]. This assumption involves two hypotheses: first, that [math]\displaystyle{ \Pi(k) }[/math] depends on [math]\displaystyle{ k }[/math], in contrast to random graphs in which [math]\displaystyle{ \Pi(k) = p }[/math], and second, that the functional form of [math]\displaystyle{ \Pi(k) }[/math] is linear in [math]\displaystyle{ k }[/math]. The precise form of [math]\displaystyle{ \Pi(k) }[/math] is not necessarily linear, and recent studies have demonstrated that the degree distribution depends strongly on [math]\displaystyle{ \Pi(k) }[/math]
The Barabási–Albert model assumes that the probability [math]\displaystyle{ \Pi(k) }[/math] that a node attaches to node [math]\displaystyle{ i }[/math] is proportional to the degree [math]\displaystyle{ k }[/math] of node [math]\displaystyle{ i }[/math]. This assumption involves two hypotheses: first, that [math]\displaystyle{ \Pi(k) }[/math] depends on [math]\displaystyle{ k }[/math], in contrast to random graphs in which [math]\displaystyle{ \Pi(k) = p }[/math], and second, that the functional form of [math]\displaystyle{ \Pi(k) }[/math] is linear in [math]\displaystyle{ k }[/math]. The precise form of [math]\displaystyle{ \Pi(k) }[/math] is not necessarily linear, and recent studies have demonstrated that the degree distribution depends strongly on [math]\displaystyle{ \Pi(k) }[/math]
Barab si-Albert 模型假定节点数学 i / math 的概率数学[ Pi (k) / math ]与节点数学 i / math 的度数学[ k / math ]成正比。这个假设包括两个假设: 第一,数学 Pi (k) / 数学依赖于数学 k / math,与数学 Pi (k) p / math 的随机图形形成对比,第二,数学 Pi (k) / math 的函数形式在数学 k / math 中是线性的。数学 Pi (k) / math 的精确形式不一定是线性的,最近的研究表明度分布强烈依赖于数学 Pi (k) / math
Krapivsky, Redner, and Leyvraz[35] demonstrate that the scale-free nature of the network is destroyed for nonlinear preferential attachment. The only case in which the topology of the network is scale free is that in which the preferential attachment is asymptotically linear, i.e. [math]\displaystyle{ \Pi(k_i) \sim a_\infty k_i }[/math] as [math]\displaystyle{ k_i \to \infty }[/math]. In this case the rate equation leads to
Krapivsky, Redner, and Leyvraz demonstrate that the scale-free nature of the network is destroyed for nonlinear preferential attachment. The only case in which the topology of the network is scale free is that in which the preferential attachment is asymptotically linear, i.e. [math]\displaystyle{ \Pi(k_i) \sim a_\infty k_i }[/math] as [math]\displaystyle{ k_i \to \infty }[/math]. In this case the rate equation leads to
Krapivsky,Redner 和 Leyvraz 证明了网络的无标度性质被非线性优先连接所破坏。网络拓扑是无标度的唯一情况是优先连接是渐近线性的,即。数学 Pi (ki) sim a infty k i / math as math k i to infty / math。在这种情况下,速率方程导致
- [math]\displaystyle{ P(k) \sim k^{-\gamma}\text{ with }\gamma = 1 + \frac \mu {a_\infty}. }[/math]
[math]\displaystyle{ P(k) \sim k^{-\gamma}\text{ with }\gamma = 1 + \frac \mu {a_\infty}. }[/math]
数学 p (k) sim k ^ { gamma } text { with } gamma 1 + frac mu { a infty } . / math
This way the exponent of the degree distribution can be tuned to any value between 2 and [math]\displaystyle{ \infty }[/math].
This way the exponent of the degree distribution can be tuned to any value between 2 and [math]\displaystyle{ \infty }[/math].
通过这种方式,度分布的指数可以调整为介于2和 math infty / math 之间的任意值。
Hierarchical network model
There is another kind of scale-free model, which grows according to some patterns, such as the hierarchical network model.[39]
There is another kind of scale-free model, which grows according to some patterns, such as the hierarchical network model.
还有一种无标度模型,它是根据一些模式(如层次网络模型)发展起来的。
The iterative construction leading to a hierarchical network. Starting from a fully connected cluster of five nodes, we create four identical replicas connecting the peripheral nodes of each cluster to the central node of the original cluster. From this, we get a network of 25 nodes (N = 25).
The iterative construction leading to a hierarchical network. Starting from a fully connected cluster of five nodes, we create four identical replicas connecting the peripheral nodes of each cluster to the central node of the original cluster. From this, we get a network of 25 nodes (N = 25).
导致层次网络的迭代结构。从一个由五个节点组成的完全连接的集群开始,我们创建四个相同的副本,将每个集群的外围节点连接到原始集群的中心节点。由此,我们得到了一个由25个节点组成的网络(n25)。
Repeating the same process, we can create four more replicas of the original cluster – the four peripheral nodes of each one connect to the central node of the nodes created in the first step. This gives N = 125, and the process can continue indefinitely.
Repeating the same process, we can create four more replicas of the original cluster – the four peripheral nodes of each one connect to the central node of the nodes created in the first step. This gives N = 125, and the process can continue indefinitely.
重复同样的过程,我们可以创建原始集群的四个副本——每个集群的四个外围节点连接到第一步中创建的节点的中心节点。这给了 n 125,这个过程可以无限期地继续下去。
Fitness model
The idea is that the link between two vertices is assigned not randomly with a probability p equal for all the couple of vertices. Rather, for
The idea is that the link between two vertices is assigned not randomly with a probability p equal for all the couple of vertices. Rather, for
其思想是,两个顶点之间的链路不是随机分配的,所有顶点对的概率 p 都是相等的。更确切地说,是为了
every vertex j there is an intrinsic fitness xj and a link between vertex i and j is created with a probability
every vertex j there is an intrinsic fitness xj and a link between vertex i and j is created with a probability
每个顶点 j 都有一个内在适应度 x 子 j / sub,并且在顶点 i 和 j 之间有一个概率的连接
[math]\displaystyle{ p(x_i,x_j) }[/math].[40]
[math]\displaystyle{ p(x_i,x_j) }[/math].
数学 p (xi,xj) / 数学。
In the case of World Trade Web it is possible to reconstruct all the properties by using as fitnesses of the country their GDP, and taking
In the case of World Trade Web it is possible to reconstruct all the properties by using as fitnesses of the country their GDP, and taking
在世界贸易网络的例子中,我们可以通过利用国内生产总值来重建所有的属性,然后利用
- [math]\displaystyle{ p(x_i,x_j)=\frac {\delta x_ix_j}{1+\delta x_ix_j}. }[/math][41]
[math]\displaystyle{ p(x_i,x_j)=\frac {\delta x_ix_j}{1+\delta x_ix_j}. }[/math]
数学 p (xi,xi) frac { delta ix j }{1 + delta x ix j }。数学
Hyperbolic geometric graphs
Assuming that a network has an underlying hyperbolic geometry, one can use the framework of spatial networks to generate scale-free degree distributions. This heterogeneous degree distribution then simply reflects the negative curvature and metric properties of the underlying hyperbolic geometry.[42]
Assuming that a network has an underlying hyperbolic geometry, one can use the framework of spatial networks to generate scale-free degree distributions. This heterogeneous degree distribution then simply reflects the negative curvature and metric properties of the underlying hyperbolic geometry.
假设一个网络有一个基本的双曲几何,我们可以使用空间网络的框架来生成无标度的度分布。这种不均匀的程度分布仅仅反映了基础双曲几何的负曲率和度量属性。
Edge dual transformation to generate scale free graphs with desired properties
Starting with scale free graphs with low degree correlation and clustering coefficient, one can generate new graphs with much higher degree correlations and clustering coefficients by applying edge-dual transformation.[19]
Starting with scale free graphs with low degree correlation and clustering coefficient, one can generate new graphs with much higher degree correlations and clustering coefficients by applying edge-dual transformation.
从低度相关和集聚系数的无标度图开始,可以通过边对偶变换生成具有更高度相关性和聚类系数的新图。
Uniform-Preferential-Attachment model (UPA model)
UPA model is a variant of the preferential attachment model (proposed by Pachon et al.) which takes into account two different attachment rules: a preferential attachment mechanism (with probability 1−p) that stresses the rich get richer system, and a uniform choice (with probability p) for the most recent nodes. This modification is interesting to study the robustness of the scale-free behavior of the degree distribution. It is proved analytically that the asymptotically power-law degree distribution is preserved.[29]
UPA model is a variant of the preferential attachment model (proposed by Pachon et al.) which takes into account two different attachment rules: a preferential attachment mechanism (with probability 1−p) that stresses the rich get richer system, and a uniform choice (with probability p) for the most recent nodes. This modification is interesting to study the robustness of the scale-free behavior of the degree distribution. It is proved analytically that the asymptotically power-law degree distribution is preserved.
Upa 模型是优先连接模型的一个变体(Pachon 等人提出)它考虑了两种不同的连接规则: 强调富人变得更富有的优先连接机制(概率为1-p)和最近节点的统一选择(概率为 p)。这种修正对于研究度分布无标度行为的稳健性很有意义。解析地证明了渐近幂律度分布是保持的。
Scale-free ideal networks
In the context of network theory a scale-free ideal network is a random network with a degree distribution following the scale-free ideal gas density distribution. These networks are able to reproduce city-size distributions and electoral results by unraveling the size distribution of social groups with information theory on complex networks
In the context of network theory a scale-free ideal network is a random network with a degree distribution following the scale-free ideal gas density distribution. These networks are able to reproduce city-size distributions and electoral results by unraveling the size distribution of social groups with information theory on complex networks
在网络理论的背景下,无标度理想网络是一个遵循无标度理想气体密度分布的度分布的随机网络。这些网络能够再现城市规模分布和选举结果通过解开规模分布的社会群体的信息理论在复杂的网络
when a competitive cluster growth process is applied to the network.[43]引用错误:没有找到与</ref>对应的<ref>标签 In models of scale-free ideal networks it is possible to demonstrate that Dunbar's number is the cause of the phenomenon known as the 'six degrees of separation' .
</ref> In models of scale-free ideal networks it is possible to demonstrate that Dunbar's number is the cause of the phenomenon known as the 'six degrees of separation' .
/ ref 在无标度理想网络模型中,有可能证明邓巴数是所谓“六度分隔理论”现象的原因。
Novel characteristics
For a scale-free network with [math]\displaystyle{ n }[/math] nodes and power-law exponent [math]\displaystyle{ \beta\gt 3 }[/math], the induced subgraph constructed by vertices with degrees larger than [math]\displaystyle{ \log{n}\times \log^{*}{n} }[/math] is a scale-free network with [math]\displaystyle{ \beta'=2 }[/math], almost surely (a.s.).[44]
For a scale-free network with [math]\displaystyle{ n }[/math] nodes and power-law exponent [math]\displaystyle{ \beta\gt 3 }[/math], the induced subgraph constructed by vertices with degrees larger than [math]\displaystyle{ \log{n}\times \log^{*}{n} }[/math] is a scale-free network with [math]\displaystyle{ \beta'=2 }[/math], almost surely (a.s.).
对于一个具有数学 n / 数学节点和幂律指数 math β3 / math 的无尺度网络,由比 math log n n }乘以 log n ^ * math 大度的顶点构成的诱导子图几乎可以肯定是一个具有 math β2 / math 的无尺度网络。
See also
References
- ↑ Onnela, J. -P.; Saramaki, J.; Hyvonen, J.; Szabo, G.; Lazer, D.; Kaski, K.; Kertesz, J.; Barabasi, A. -L. (2007). "Structure and tie strengths in mobile communication networks". Proceedings of the National Academy of Sciences. 104 (18): 7332–7336. arXiv:physics/0610104. Bibcode:2007PNAS..104.7332O. doi:10.1073/pnas.0610245104. PMC 1863470. PMID 17456605.
- ↑ Choromański, K.; Matuszak, M.; MiȩKisz, J. (2013). "Scale-Free Graph with Preferential Attachment and Evolving Internal Vertex Structure". Journal of Statistical Physics. 151 (6): 1175–1183. Bibcode:2013JSP...151.1175C. doi:10.1007/s10955-013-0749-1.
- ↑ 3.0 3.1 Clauset, Aaron; Cosma Rohilla Shalizi; M. E. J Newman (2009). "Power-law distributions in empirical data". SIAM Review. 51 (4): 661–703. arXiv:0706.1062. Bibcode:2009SIAMR..51..661C. doi:10.1137/070710111.
- ↑ Broido, Anna; Aaron Clauset (2019-03-04). "Scale-free networks are rare". Nature Communications. 10 (1): 1017. arXiv:1801.03400. doi:10.1038/s41467-019-08746-5. PMC 6399239. PMID 30833554.
- ↑ Among the seven examples studied by Amaral et al, six of them where single-scale and only example iii, the movie-actor network had a power law regime followed by a sharp cutoff. None of Amaral et al's examples obeyed the power law regime for large k, i.e. none of these seven examples were shown to be scale-free. See especially the beginning of the discussion section of Amaral LAN, Scala A, Barthelemy M, Stanley HE (2000). "Classes of small-world networks". PNAS. 97 (21): 11149–52. arXiv:cond-mat/0001458. doi:10.1073/pnas.200327197. PMC 17168. PMID 11005838.
- ↑ Dorogovtsev, S.; Mendes, J.; Samukhin, A. (2000). "Structure of Growing Networks with Preferential Linking". Physical Review Letters. 85 (21): 4633–4636. arXiv:cond-mat/0004434. Bibcode:2000PhRvL..85.4633D. doi:10.1103/PhysRevLett.85.4633. PMID 11082614.
- ↑ Bollobás, B.; Riordan, O.; Spencer, J.; Tusnády, G. (2001). "The degree sequence of a scale-free random graph process". Random Structures and Algorithms. 18 (3): 279–290. doi:10.1002/rsa.1009. MR 1824277.
- ↑ Dorogovtsev, S. N.; Mendes, J. F. F. (2002). "Evolution of networks". Advances in Physics. 51 (4): 1079–1187. arXiv:cond-mat/0106144. Bibcode:2002AdPhy..51.1079D. doi:10.1080/00018730110112519.
- ↑ 引用错误:无效
<ref>标签;未给name属性为Emergence of scaling in random netw的引用提供文字 - ↑ 引用错误:无效
<ref>标签;未给name属性为NETWORK BIOLOGY: UNDERSTANDING THE的引用提供文字 - ↑ 11.0 11.1 11.2 Cohen, Reoven; Erez, K.; ben-Avraham, D.; Havlin, S. (2001). "Breakdown of the Internet under Intentional Attack". Physical Review Letters. 86 (16): 3682–5. arXiv:cond-mat/0010251. Bibcode:2001PhRvL..86.3682C. doi:10.1103/PhysRevLett.86.3682. PMID 11328053.
- ↑ 12.0 12.1 Callaway, Duncan S.; Newman, M. E. J.; Strogatz, S. H.; Watts, D. J. (2000). "Network Robustness and Fragility: Percolation on Random Graphs". Physical Review Letters. 85 (25): 5468–71. arXiv:cond-mat/0007300. Bibcode:2000PhRvL..85.5468C. doi:10.1103/PhysRevLett.85.5468. PMID 11136023.
- ↑ Cohen, Reuven; Erez, Keren; ben-Avraham, Daniel; Havlin, Shlomo (2000). "Resilience of the Internet to Random Breakdowns". Physical Review Letters. 85 (21): 4626–4628. arXiv:cond-mat/0007048. Bibcode:2000PhRvL..85.4626C. doi:10.1103/PhysRevLett.85.4626. PMID 11082612.
- ↑ S. Shao, X. Huang, H.E. Stanley, S. Havlin (2015). "Percolation of localized attack on complex networks". New J. Phys (17): 023049.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ Cohen, Reuven; Havlin, Shlomo (2003). "Scale-Free Networks Are Ultrasmall". Physical Review Letters. 90 (5): 058701. arXiv:cond-mat/0205476. Bibcode:2003PhRvL..90e8701C. doi:10.1103/PhysRevLett.90.058701. PMID 12633404.
- ↑ 引用错误:无效
<ref>标签;未给name属性为qwe的引用提供文字 - ↑ R. Cohen, S. Havlin, D. Ben-Avraham (2003). "Efficient immunization strategies for computer networks and populations". Phys. Rev. Lett (91): 247901. doi:10.1103/PhysRevLett.91.247901.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ Y. Chen, G. Paul, S. Havlin, F. Liljeros, H.E. Stanley (2008). "Finding a Better Immunization Strategy". Phys. Rev. Lett (101): 058701. doi:10.1103/PhysRevLett.101.058701.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ 19.0 19.1 Ramezanpour, A.; Karimipour, V.; Mashaghi, A. (2003). "Generating correlated networks from uncorrelated ones". Phys. Rev. E. 67 (4): 046107. arXiv:cond-mat/0212469. Bibcode:2003PhRvE..67d6107R. doi:10.1103/PhysRevE.67.046107. PMID 12786436.
- ↑ Louridas, Panagiotis; Spinellis, Diomidis; Vlachos, Vasileios (1 September 2008). "Power laws in software". ACM Transactions on Software Engineering and Methodology. 18 (1): 2. doi:10.1145/1391984.1391986.
- ↑ Papoudakis, Georgios; Preux, Philippe; Monperrus, Martin (27 November 2017). "A Generative Model for Sparse, Evolving Digraphs". Studies in Computational Intelligence. 689: 531–542. arXiv:1710.06298. doi:10.1007/978-3-319-72150-7_43. ISBN 978-3-319-72149-1.
- ↑ De Masi, Giulia; et al. (2006). "Fitness model for the Italian interbank money market". Physical Review E. 74 (6): 066112. arXiv:physics/0610108. Bibcode:2006PhRvE..74f6112D. doi:10.1103/PhysRevE.74.066112. PMID 17280126.
- ↑ Soramäki, Kimmo; et al. (2007). "The topology of interbank payment flows". Physica A: Statistical Mechanics and Its Applications. 379 (1): 317–333. Bibcode:2007PhyA..379..317S. doi:10.1016/j.physa.2006.11.093. hdl:10419/60649.
- ↑ Steyvers, Mark; Joshua B. Tenenbaum (2005). "The Large-Scale Structure of Semantic Networks: Statistical Analyses and a Model of Semantic Growth". Cognitive Science. 29 (1): 41–78. arXiv:cond-mat/0110012. doi:10.1207/s15516709cog2901_3. PMID 21702767.
- ↑ Fratini, Michela; Poccia, Nicola; Ricci, Alessandro; Campi, Gaetano; Burghammer, Manfred; Aeppli, Gabriel; Bianconi, Antonio (2010). "Scale-free structural organization of oxygen interstitials in La2CuO4+y". Nature. 466 (7308): 841–4. arXiv:1008.2015. Bibcode:2010Natur.466..841F. doi:10.1038/nature09260. PMID 20703301.
- ↑ Poccia, Nicola; Ricci, Alessandro; Campi, Gaetano; Fratini, Michela; Puri, Alessandro; Di Gioacchino, Daniele; Marcelli, Augusto; Reynolds, Michael; Burghammer, Manfred; Saini, Naurang L.; Aeppli, Gabriel; Bianconi, Antonio (2012). "Optimum inhomogeneity of local lattice distortions in La2CuO4+y". PNAS. 109 (39): 15685–15690. arXiv:1208.0101. Bibcode:2012PNAS..10915685P. doi:10.1073/pnas.1208492109. PMC 3465392. PMID 22961255.
- ↑ Hassan, M. K.; Hassan, M. Z.; Pavel, N. I. (2010). "Scale-free network topology and multifractality in a weighted planar stochastic lattice". New Journal of Physics. 12 (9): 093045. doi:10.1088/1367-2630/12/9/093045.
- ↑ Hassan, M. K.; Hassan, M. Z.; Pavel, N. I. (2010). "Scale-free coordination number disorder and multifractal size disorder in weighted planar stochastic lattice". J. Phys.: Conf. Ser. 297: 01.
- ↑ 29.0 29.1 29.2 Pachon, Angelica; Sacerdote, Laura; Yang, Shuyi (2018). "Scale-free behavior of networks with the copresence of preferential and uniform attachment rules". Physica D: Nonlinear Phenomena. 371: 1–12. arXiv:1704.08597. Bibcode:2018PhyD..371....1P. doi:10.1016/j.physd.2018.01.005.
- ↑ Kumar, Ravi; Raghavan, Prabhakar (2000). Stochastic Models for the Web Graph (PDF). Foundations of Computer Science, 41st Annual Symposium on. pp. 57–65. doi:10.1109/SFCS.2000.892065.
- ↑ 31.0 31.1 Dangalchev Ch., Generation models for scale-free networks, Physica A 338, 659 (2004).
- ↑ Barabási, A.-L. and R. Albert, Science 286, 509 (1999).
- ↑ R. Albert, and A.L. Barabási, Phys. Rev. Lett. 85, 5234(2000).
- ↑ S. N. Dorogovtsev, J. F. F. Mendes, and A. N. Samukhim, cond-mat/0011115.
- ↑ 35.0 35.1 P.L. Krapivsky, S. Redner, and F. Leyvraz, Phys. Rev. Lett. 85, 4629 (2000).
- ↑ B. Tadic, Physica A 293, 273(2001).
- ↑ S. Bomholdt and H. Ebel, cond-mat/0008465; H.A. Simon, Bimetrika 42, 425(1955).
- ↑ Hassan, M. K.; Islam, Liana; Arefinul Haque, Syed (2017). "Degree distribution, rank-size distribution, and leadership persistence in mediation-driven attachment networks". Physica A. 469: 23–30. arXiv:1411.3444. Bibcode:2017PhyA..469...23H. doi:10.1016/j.physa.2016.11.001.
- ↑ Ravasz, E.; Barabási (2003). "Hierarchical organization in complex networks". Phys. Rev. E. 67 (2): 026112. arXiv:cond-mat/0206130. Bibcode:2003PhRvE..67b6112R. doi:10.1103/physreve.67.026112. PMID 12636753.
- ↑ Caldarelli, G.; et al. (2002). "Scale-free networks from varying vertex intrinsic fitness" (PDF). Phys. Rev. Lett. 89 (25): 258702. Bibcode:2002PhRvL..89y8702C. doi:10.1103/physrevlett.89.258702. PMID 12484927.
- ↑ Garlaschelli, D.; et al. (2004). "Fitness-Dependent Topological Properties of the World Trade Web". Phys. Rev. Lett. 93 (18): 188701. arXiv:cond-mat/0403051. Bibcode:2004PhRvL..93r8701G. doi:10.1103/physrevlett.93.188701. PMID 15525215.
- ↑ Krioukov, Dmitri; Papadopoulos, Fragkiskos; Kitsak, Maksim; Vahdat, Amin; Boguñá, Marián (2010). "Hyperbolic geometry of complex networks". Physical Review E. 82 (3): 036106. arXiv:1006.5169. Bibcode:2010PhRvE..82c6106K. doi:10.1103/PhysRevE.82.036106. PMID 21230138.
- ↑ A. Hernando; D. Villuendas; C. Vesperinas; M. Abad; A. Plastino (2009). "Unravelling the size distribution of social groups with information theory on complex networks". arXiv:0905.3704 [physics.soc-ph]., submitted to European Physical Journal B
- ↑ Heydari, H.; Taheri, S.M.; Kaveh, K. (2018). "Distributed Maximal Independent Set on Scale-Free Networks". arXiv:1804.02513 [cs.DC].
Further reading
- Albert R.; Barabási A.-L. (2002). "Statistical mechanics of complex networks". Rev. Mod. Phys. 74 (1): 47–97. arXiv:cond-mat/0106096. Bibcode:2002RvMP...74...47A. doi:10.1103/RevModPhys.74.47.
- Amaral LAN, Scala A, Barthelemy M, Stanley HE (2000). "Classes of small-world networks". PNAS. 97 (21): 11149–52. arXiv:cond-mat/0001458. Bibcode:2000PNAS...9711149A. doi:10.1073/pnas.200327197. PMC 17168. PMID 11005838.
- Barabási, Albert-László (2004). Linked: How Everything is Connected to Everything Else. ISBN 0-452-28439-2. https://archive.org/details/linkedhoweveryth00bara.
- Barabási, Albert-László; Bonabeau, Eric (May 2003). "Scale-Free Networks" (PDF). Scientific American. 288 (5): 50–9. Bibcode:2003SciAm.288e..60B. doi:10.1038/scientificamerican0503-60.
- Dan Braha; Yaneer Bar-Yam (2004). "Topology of Large-Scale Engineering Problem-Solving Networks" (PDF). Phys. Rev. E. 69 (1): 016113. Bibcode:2004PhRvE..69a6113B. doi:10.1103/PhysRevE.69.016113. PMID 14995673.
- Caldarelli G. "Scale-Free Networks" Oxford University Press, Oxford (2007).
- Caldarelli G.; Capocci A.; De Los Rios P.; Muñoz M.A. (2002). "Scale-free networks from varying vertex intrinsic fitness". Physical Review Letters. 89 (25): 258702. arXiv:cond-mat/0207366. Bibcode:2002PhRvL..89y8702C. doi:10.1103/PhysRevLett.89.258702. PMID 12484927.
- R. Cohen; K. Erez; D. ben-Avraham; S. Havlin (2000). "Resilience of the Internet to Random Breakdowns". Phys. Rev. Lett. 85 (21): 4626–8. arXiv:cond-mat/0007048. Bibcode:2000PhRvL..85.4626C. doi:10.1103/PhysRevLett.85.4626. PMID 11082612.
- R. Cohen; K. Erez; D. ben-Avraham; S. Havlin (2001). "Breakdown of the Internet under Intentional Attack". Phys. Rev. Lett. 86 (16): 3682–5. arXiv:cond-mat/0010251. Bibcode:2001PhRvL..86.3682C. doi:10.1103/PhysRevLett.86.3682. PMID 11328053.
- R. Cohen; K. Erez; D. ben-Avraham; S. Havlin (2002). "Scale-free networks on lattices". Phys. Rev. Lett. 89 (21): 218701. arXiv:cond-mat/0205613. Bibcode:2002PhRvL..89u8701R. doi:10.1103/physrevlett.89.218701. PMID 12443452.
- Dangalchev, Ch. (2004). "Generation models for scale-free networks". Physica A. 338 (3–4): 659–671. Bibcode:2004PhyA..338..659D. doi:10.1016/j.physa.2004.01.056.
- Dorogovtsev, S.N.; Mendes, J.F.F.; Samukhin, A.N. (2000). "Structure of Growing Networks: Exact Solution of the Barabási—Albert's Model". Phys. Rev. Lett. 85 (21): 4633–6. arXiv:cond-mat/0004434. Bibcode:2000PhRvL..85.4633D. doi:10.1103/PhysRevLett.85.4633. PMID 11082614.
- Dorogovtsev, S.N.; Mendes, J.F.F. (2003). Evolution of Networks: from biological networks to the Internet and WWW. Oxford University Press. ISBN 0-19-851590-1.
- Dorogovtsev, S.N.; Goltsev A.V.; Mendes, J.F.F. (2008). "Critical phenomena in complex networks". Rev. Mod. Phys. 80 (4): 1275–1335. arXiv:0705.0010. Bibcode:2008RvMP...80.1275D. doi:10.1103/RevModPhys.80.1275.
- Dorogovtsev, S.N.; Mendes, J.F.F. (2002). "Evolution of networks". Advances in Physics. 51 (4): 1079–1187. arXiv:cond-mat/0106144. Bibcode:2002AdPhy..51.1079D. doi:10.1080/00018730110112519.
- Erdős, P.; Rényi, A. (1960). On the Evolution of Random Graphs. 5. Publication of the Mathematical Institute of the Hungarian Academy of Science. pp. 17–61. http://www.math-inst.hu/~p_erdos/1960-10.pdf.
- Faloutsos, M.; Faloutsos, P.; Faloutsos, C. (1999). "On power-law relationships of the internet topology". Comp. Comm. Rev. 29 (4): 251–262. doi:10.1145/316194.316229.
- Li, L.; Alderson, D.; Tanaka, R.; Doyle, J.C.; Willinger, W. (2005). "Towards a Theory of Scale-Free Graphs: Definition, Properties, and Implications (Extended Version)". arXiv:cond-mat/0501169.
- Kumar, R.; Raghavan, P.; Rajagopalan, S.; Sivakumar, D.; Tomkins, A.; Upfal, E. (2000). Stochastic models for the web graph (PDF). Redondo Beach, CA: IEEE CS Press. pp. 57–65.
{{cite conference}}: Unknown parameter|booktitle=ignored (help)
- Matlis, Jan (November 4, 2002). "Scale-Free Networks".
- Newman, Mark E.J. (2003). "The structure and function of complex networks". SIAM Review. 45 (2): 167–256. arXiv:cond-mat/0303516. Bibcode:2003SIAMR..45..167N. doi:10.1137/S003614450342480.
- Pastor-Satorras, R.; Vespignani, A. (2004). Evolution and Structure of the Internet: A Statistical Physics Approach. Cambridge University Press. ISBN 0-521-82698-5.
- Pennock, D.M.; Flake, G.W.; Lawrence, S.; Glover, E.J.; Giles, C.L. (2002). "Winners don't take all: Characterizing the competition for links on the web". PNAS. 99 (8): 5207–11. Bibcode:2002PNAS...99.5207P. doi:10.1073/pnas.032085699. PMC 122747. PMID 16578867.
- Robb, John. Scale-Free Networks and Terrorism, 2004.
- Keller, E.F. (2005). "Revisiting "scale-free" networks". BioEssays. 27 (10): 1060–8. doi:10.1002/bies.20294. PMID 16163729.https://en.wikipedia.org/wiki/Defekte_Weblinks?dwl={{{url}}} Seite nicht mehr abrufbar], Suche in Webarchiven: Kategorie:Wikipedia:Weblink offline (andere Namensräume)[http://timetravel.mementoweb.org/list/2010/Kategorie:Wikipedia:Vorlagenfehler/Vorlage:Toter Link/URL_fehlt 模板:Cbignore
- Onody, R.N.; de Castro, P.A. (2004). "Complex Network Study of Brazilian Soccer Player". Phys. Rev. E. 70 (3): 037103. arXiv:cond-mat/0409609. Bibcode:2004PhRvE..70c7103O. doi:10.1103/PhysRevE.70.037103. PMID 15524675.
- Reuven Cohen; Shlomo Havlin (2003). "Scale-Free Networks are Ultrasmall". Phys. Rev. Lett. 90 (5): 058701. arXiv:cond-mat/0205476. Bibcode:2003PhRvL..90e8701C. doi:10.1103/PhysRevLett.90.058701. PMID 12633404.
- Kasthurirathna, D.; Piraveenan, M. (2015). "Complex Network Study of Brazilian Soccer Player". Sci. Rep. In Press.
Category:Graph families
类别: 图族
This page was moved from wikipedia:en:Scale-free network. Its edit history can be viewed at 无标度网络模型/edithistory