模拟退火

此词条暂由彩云小译翻译，未经人工整理和审校，带来阅读不便，请见谅。

}}

Simulated Annealing can be used to solve combinatorial problems. Here it is applied to the travelling salesman problem to minimize the length of a route that connects all 125 points.

模拟退火可以用来解决组合问题。这里我们将它应用到[[旅行推销员问题最小化连接所有125个点的路径长度]。]

Simulated annealing (SA) is a probabilistic technique for approximating the global optimum of a given function. Specifically, it is a metaheuristic to approximate global optimization in a large search space for an optimization problem. It is often used when the search space is discrete (e.g., the traveling salesman problem). For problems where finding an approximate global optimum is more important than finding a precise local optimum in a fixed amount of time, simulated annealing may be preferable to alternatives such as gradient descent.

Simulated annealing (SA) is a probabilistic technique for approximating the global optimum of a given function. Specifically, it is a metaheuristic to approximate global optimization in a large search space for an optimization problem. It is often used when the search space is discrete (e.g., the traveling salesman problem). For problems where finding an approximate global optimum is more important than finding a precise local optimum in a fixed amount of time, simulated annealing may be preferable to alternatives such as gradient descent.

是一种用于逼近给定函数全局最优值的概率模拟退火。具体来说，它是一个亚启发式近似全局优化在一个大的搜索空间为最佳化问题。当搜索空间是离散的(例如，旅行推销员问题)时，经常使用它。对于那些在一定时间内找到一个近似的全局最优解比找到一个精确的局部最优解更重要的问题，模拟退火可能比诸如梯度下降法之类的替代方法更可取。

The name and inspiration come from annealing in metallurgy, a technique involving heating and controlled cooling of a material to increase the size of its crystals and reduce their defects. Both are attributes of the material that depend on its thermodynamic free energy. Heating and cooling the material affects both the temperature and the thermodynamic free energy.

这个名字和灵感来自于冶金学中的退火，这种技术包括对材料进行加热和控制冷却，以增加其晶体的尺寸并减少其缺陷。两者都是材料的属性，取决于它的热力学自由能。加热和冷却材料都会影响温度和热力学自由能。

Simulated annealing can be used to approximate the global minimum for a function with many variables. In 1983, this approach was used by Kirkpatrick, Gelatt Jr.,Vecchi, ^[1] for a solution of the traveling salesman problem. They also proposed its current name, simulated annealing.

Simulated annealing can be used to approximate the global minimum for a function with many variables. In 1983, this approach was used by Kirkpatrick, Gelatt Jr.,Vecchi, for a solution of the traveling salesman problem. They also proposed its current name, simulated annealing.

模拟退火可以用来逼近具有多个变量的函数的全局最小值。1983年，这种方法被柯克帕特里克、小格拉特和维奇用来解决旅行推销员问题。他们还提出了它现在的名字---- 模拟退火。

This notion of slow cooling implemented in the simulated annealing algorithm is interpreted as a slow decrease in the probability of accepting worse solutions as the solution space is explored. Accepting worse solutions is a fundamental property of metaheuristics because it allows for a more extensive search for the global optimal solution. In general, simulated annealing algorithms work as follows. The temperature progressively decreases from an initial positive value to zero. At each time step, the algorithm randomly selects a solution close to the current one, measures its quality, and moves to it according to the temperature-dependent probabilities of selecting better or worse solutions, which during the search respectively remain at 1 (or positive) and decrease towards zero.

模拟退火算法中实现的缓慢冷却的概念被解释为在探索解决方案空间时接受较差解决方案的概率缓慢下降。接受较差的解是元启发法的一个基本属性，因为它允许对全局最优解进行更广泛的搜索。一般来说，模拟退火算法的工作原理如下。温度从最初的正值逐渐降低到零。该算法在每个时间步随机选择一个接近当前解的解，测量其质量，并根据温度相关的概率选择更好或更坏的解，在搜索过程中分别保持在1(或正)和向零递减。

The simulation can be performed either by a solution of kinetic equations for density functions^[2]^[3] or by using the stochastic sampling method.^[1]^[4] The method is an adaptation of the Metropolis–Hastings algorithm, a Monte Carlo method to generate sample states of a thermodynamic system, published by N. Metropolis et al. in 1953.^[5]

The simulation can be performed either by a solution of kinetic equations for density functions or by using the stochastic sampling method. The method is an adaptation of the Metropolis–Hastings algorithm, a Monte Carlo method to generate sample states of a thermodynamic system, published by N. Metropolis et al. in 1953.

模拟可以通过求解密度函数的动力学方程或采用随机抽样方法进行。这种方法是对 Metropolis-Hastings 算法的一种改进，该算法是一种用来生成蒙特卡罗方法热力学系统状态样本的方法，由 n. Metropolis 等人发表。1953年。

Overview

The state of some physical systems, and the function E(s) to be minimized, is analogous to the internal energy of the system in that state. The goal is to bring the system, from an arbitrary initial state, to a state with the minimum possible energy.

The state of some physical systems, and the function E(s) to be minimized, is analogous to the internal energy of the system in that state. The goal is to bring the system, from an arbitrary initial state, to a state with the minimum possible energy.

某些物理系统的状态，以及要最小化的函数 e (s) ，类似于处于该状态的系统的内能。我们的目标是使系统，从一个任意的初始状态，到一个能量最小的状态。

Simulated annealing searching for a maximum. The objective here is to get to the highest point; however, it is not enough to use a simple hill climb algorithm, as there are many local maxima. By cooling the temperature slowly the global maximum is found.

hill climb algorithm, as there are many local maxima. By cooling the temperature slowly the global maximum is found.|500px]]

爬山算法，因为有许多局部极大值。通过慢慢降温，我们发现了全球最大温度。 | 500px ]

The basic iteration

At each step, the simulated annealing heuristic considers some neighboring state s* of the current state s, and probabilistically decides between moving the system to state s* or staying in-state s. These probabilities ultimately lead the system to move to states of lower energy. Typically this step is repeated until the system reaches a state that is good enough for the application, or until a given computation budget has been exhausted.

在每个步骤中，模拟退火启发式考虑当前状态的一些相邻状态 s * ，然后根据概率决定是将系统移动到状态 s * 还是保持在状态 s * 。这些可能性最终导致系统进入低能状态。通常，这个步骤会重复进行，直到系统达到对应用程序足够好的状态，或者直到给定的计算预算用完。

The neighbours of a state

Optimization of a solution involves evaluating the neighbours of a state of the problem, which are new states produced through conservatively altering a given state. For example, in the travelling salesman problem each state is typically defined as a permutation of the cities to be visited, and its neighbours are the set of permutations produced by reversing the order of any two successive cities. The well-defined way in which the states are altered to produce neighbouring states is called a "move", and different moves give different sets of neighbouring states. These moves usually result in minimal alterations of the last state, in an attempt to progressively improve the solution through iteratively improving its parts (such as the city connections in the traveling salesman problem).

解决方案的优化包括评估问题状态的邻居，这些邻居是通过保守地改变给定状态而产生的新状态。例如，在中东旅行推销员问题，每个州通常被定义为要参观的城市的排列，而其邻州则是通过颠倒任意两个连续城市的顺序而产生的排列组合。这种明确界定的改变各国以产生邻国的方式被称为“移动” ，不同的移动会产生不同的邻国集合。这些移动通常会导致最后一个状态的最小改变，以尝试通过迭代改进解决方案的各个部分(例如旅行推销员问题中的城市连接)来逐步改进解决方案。

Simple heuristics like hill climbing, which move by finding better neighbour after better neighbour and stop when they have reached a solution which has no neighbours that are better solutions, cannot guarantee to lead to any of the existing better solutions模板:Snd their outcome may easily be just a local optimum, while the actual best solution would be a global optimum that could be different. Metaheuristics use the neighbours of a solution as a way to explore the solutions space, and although they prefer better neighbours, they also accept worse neighbours in order to avoid getting stuck in local optima; they can find the global optimum if run for a long enough amount of time.

Simple heuristics like hill climbing, which move by finding better neighbour after better neighbour and stop when they have reached a solution which has no neighbours that are better solutions, cannot guarantee to lead to any of the existing better solutions their outcome may easily be just a local optimum, while the actual best solution would be a global optimum that could be different. Metaheuristics use the neighbours of a solution as a way to explore the solutions space, and although they prefer better neighbours, they also accept worse neighbours in order to avoid getting stuck in local optima; they can find the global optimum if run for a long enough amount of time.

像爬山这样的简单的启发式方法，通过寻找更好的邻居来寻找更好的邻居，当他们达成一个没有更好的邻居的解决方案时就停止，不能保证会导致任何现有的更好的解决方案，他们的结果可能很容易地只是一个局部的最佳解决方案，而实际的最佳解决方案将是一个可能不。元启发法利用解的邻域作为探索解空间的方法，尽管它们更喜欢更好的邻域，但它们也接受更差的邻域以避免陷入局部最优; 如果运行足够长的时间，它们可以找到全局最优。

Acceptance probabilities

The probability of making the transition from the current state [math]\displaystyle{ s }[/math] to a candidate new state [math]\displaystyle{ s' }[/math] is specified by an acceptance probability function [math]\displaystyle{ P(e, e', T) }[/math], that depends on the energies [math]\displaystyle{ e = E(s) }[/math] and [math]\displaystyle{ e' = E(s') }[/math] of the two states, and on a global time-varying parameter [math]\displaystyle{ T }[/math] called the temperature. States with a smaller energy are better than those with a greater energy. The probability function [math]\displaystyle{ P }[/math] must be positive even when [math]\displaystyle{ e' }[/math] is greater than [math]\displaystyle{ e }[/math]. This feature prevents the method from becoming stuck at a local minimum that is worse than the global one.

The probability of making the transition from the current state [math]\displaystyle{ s }[/math] to a candidate new state [math]\displaystyle{ s' }[/math] is specified by an acceptance probability function [math]\displaystyle{ P(e, e', T) }[/math], that depends on the energies [math]\displaystyle{ e = E(s) }[/math] and [math]\displaystyle{ e' = E(s') }[/math] of the two states, and on a global time-varying parameter [math]\displaystyle{ T }[/math] called the temperature. States with a smaller energy are better than those with a greater energy. The probability function [math]\displaystyle{ P }[/math] must be positive even when [math]\displaystyle{ e' }[/math] is greater than [math]\displaystyle{ e }[/math]. This feature prevents the method from becoming stuck at a local minimum that is worse than the global one.

从当前状态数学到候选状态数学的转变概率是由接受概率密度函数 / 数学 p (e，e’ ，t) / 数学确定的，这取决于两个状态的能量数学 e (s) / 数学 e (s’) / 数学，以及全球时变参数数学 t / 数学，称为温度。能量较小的状态比能量较大的状态要好。概率密度函数的数学 p / 数学必须是积极的，即使数学 e / 数学大于数学 e / 数学。这个特性可以防止方法陷入比全局最小值更糟糕的局部最小值。

When [math]\displaystyle{ T }[/math] tends to zero, the probability [math]\displaystyle{ P(e, e', T) }[/math] must tend to zero if [math]\displaystyle{ e' \gt e }[/math] and to a positive value otherwise. For sufficiently small values of [math]\displaystyle{ T }[/math], the system will then increasingly favor moves that go "downhill" (i.e., to lower energy values), and avoid those that go "uphill." With [math]\displaystyle{ T=0 }[/math] the procedure reduces to the greedy algorithm, which makes only the downhill transitions.

当数学 t / math 趋于零时，如果 math e / math 趋于零，概率数学 p (e，e’ ，t) / math 必须趋于零，否则趋于正值。对于足够小的数学 t / math 值，系统会越来越倾向于走“下坡路”(即降低能量值) ，而避免走“上坡路”使用数学 t0 / math，过程简化为贪婪算法，只有下坡过渡。

In the original description of simulated annealing, the probability [math]\displaystyle{ P(e, e', T) }[/math] was equal to 1 when [math]\displaystyle{ e' \lt e }[/math]—i.e., the procedure always moved downhill when it found a way to do so, irrespective of the temperature. Many descriptions and implementations of simulated annealing still take this condition as part of the method's definition. However, this condition is not essential for the method to work.

在模拟退火的原始描述中，当数学 e’ e / math 时，概率数学 p (e，e’ ，t) / math 等于1。许多模拟退火的描述和实现仍然把这个条件作为方法定义的一部分。然而，这个条件并不是这个方法工作的必要条件。

The [math]\displaystyle{ P }[/math] function is usually chosen so that the probability of accepting a move decreases when the difference

数学 p / 数学函数的选择通常是为了降低接受移动的概率

[math]\displaystyle{ e'-e }[/math] increases—that is, small uphill moves are more likely than large ones. However, this requirement is not strictly necessary, provided that the above requirements are met.

数学 e’-e / 数学增加ー也就是说，小的上坡动作比大的动作更有可能。但是，如果符合上述要求，这一要求并非绝对必要。

Given these properties, the temperature [math]\displaystyle{ T }[/math] plays a crucial role in controlling the evolution of the state [math]\displaystyle{ s }[/math] of the system with regard to its sensitivity to the variations of system energies. To be precise, for a large [math]\displaystyle{ T }[/math], the evolution of [math]\displaystyle{ s }[/math] is sensitive to coarser energy variations, while it is sensitive to finer energy variations when [math]\displaystyle{ T }[/math] is small.

考虑到这些性质，温度数学 t / math 在控制系统状态数学的演化方面起着至关重要的作用，因为它对系统能量变化的敏感性。准确地说，对于一个庞大的数学 t / math 来说，数学的进化对粗糙的能量变化是敏感的，而当数学 t / math 很小时，它对精细的能量变化是敏感的。

The annealing schedule

{{multiple image

{多重图像

| align = right

| align = right

右对齐

| total_width = 400

| total_width = 400

总宽度400

| image_gap = 0

| image_gap = 0

图像缺口0

| image1 = SimulatedAnnealingFast.jpg

| image1 = SimulatedAnnealingFast.jpg

| image1 = SimulatedAnnealingFast.jpg

| alt1 = Fast

| alt1 = Fast

1 Fast

| caption1 = Fast

| caption1 = Fast

1 Fast

| image2 = SimulatedAnnealingSlow.jpg

| image2 = SimulatedAnnealingSlow.jpg

| image2 = SimulatedAnnealingSlow.jpg

| alt2 = Slow

| alt2 = Slow

2 Slow

| caption2 = Slow

| caption2 = Slow

2慢

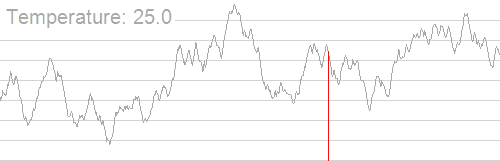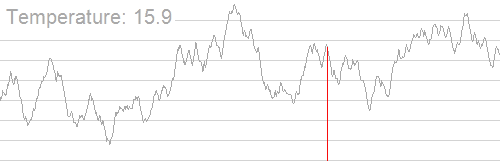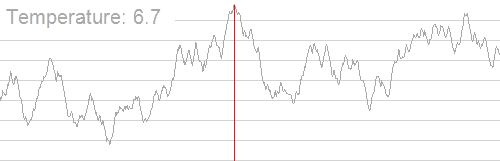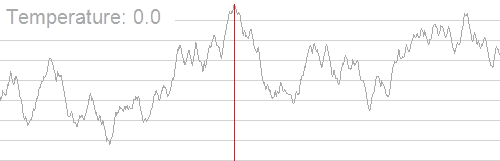
| footer= Example illustrating the effect of cooling schedule on the performance of simulated annealing. The problem is to rearrange the pixels of an image so as to minimize a certain potential energy function, which causes similar colours to attract at short range and repel at a slightly larger distance. The elementary moves swap two adjacent pixels. These images were obtained with a fast cooling schedule (left) and a slow cooling schedule (right), producing results similar to amorphous and crystalline solids, respectively.

冷却时间表对模拟退火性能的影响的例子。问题在于重新排列图像的像素点，使某个势能函数最小化，从而导致相似的颜色在短距离内相互吸引，在稍大的距离内相互排斥。Elementary 移动交换两个相邻的像素。这些图像获得了一个快速冷却时间表(左)和一个缓慢的冷却时间表(右) ，产生的结果分别类似于非晶和晶体固体。

}}

The name and inspiration of the algorithm demand an interesting feature related to the temperature variation to be embedded in the operational characteristics of the algorithm. This necessitates a gradual reduction of the temperature as the simulation proceeds. The algorithm starts initially with [math]\displaystyle{ T }[/math] set to a high value (or infinity), and then it is decreased at each step following some annealing schedule—which may be specified by the user, but must end with [math]\displaystyle{ T=0 }[/math] towards the end of the allotted time budget. In this way, the system is expected to wander initially towards a broad region of the search space containing good solutions, ignoring small features of the energy function; then drift towards low-energy regions that become narrower and narrower; and finally move downhill according to the steepest descent heuristic.

The name and inspiration of the algorithm demand an interesting feature related to the temperature variation to be embedded in the operational characteristics of the algorithm. This necessitates a gradual reduction of the temperature as the simulation proceeds. The algorithm starts initially with [math]\displaystyle{ T }[/math] set to a high value (or infinity), and then it is decreased at each step following some annealing schedule—which may be specified by the user, but must end with [math]\displaystyle{ T=0 }[/math] towards the end of the allotted time budget. In this way, the system is expected to wander initially towards a broad region of the search space containing good solutions, ignoring small features of the energy function; then drift towards low-energy regions that become narrower and narrower; and finally move downhill according to the steepest descent heuristic.

算法的名称和灵感要求在算法的运行特性中嵌入一个与温度变化有关的有趣特征。这需要随着模拟的进行逐渐降低温度。该算法首先将 math t / math 设置为一个高值(或无穷大) ，然后按照某种退火时间表(可能由用户指定，但必须在分配的时间预算结束时以 math t 0 / math 结束)逐步减少。通过这种方式，系统被期望最初走向包含良好解的搜索空间的广阔区域，忽略能量函数的小特征; 然后向越来越窄的低能量区域漂移; 最后根据梯度下降法启发式向下移动。

For any given finite problem, the probability that the simulated annealing algorithm terminates with a global optimal solution approaches 1 as the annealing schedule is extended.^[6] This theoretical result, however, is not particularly helpful, since the time required to ensure a significant probability of success will usually exceed the time required for a complete search of the solution space.^{[citation needed]}

For any given finite problem, the probability that the simulated annealing algorithm terminates with a global optimal solution approaches 1 as the annealing schedule is extended. This theoretical result, however, is not particularly helpful, since the time required to ensure a significant probability of success will usually exceed the time required for a complete search of the solution space.

对于任何给定的有限问题，随着退火时间表的扩展，模拟退火算法终止于全局最优解的概率接近1。然而，这一理论结果并不特别有用，因为确保取得重大成功的可能性所需的时间通常超过完全搜索解决方案空间所需的时间。

Pseudocode

The following pseudocode presents the simulated annealing heuristic as described above. It starts from a state $s 0$ and continues until a maximum of $k max$ steps have been taken. In the process, the call $neighbour(s)$ should generate a randomly chosen neighbour of a given state $s$ ; the call $random(0, 1)$ should pick and return a value in the range $[0, 1]$ , uniformly at random. The annealing schedule is defined by the call $temperature(r)$ , which should yield the temperature to use, given the fraction $r$ of the time budget that has been expended so far.

The following pseudocode presents the simulated annealing heuristic as described above. It starts from a state and continues until a maximum of steps have been taken. In the process, the call should generate a randomly chosen neighbour of a given state ; the call should pick and return a value in the range , uniformly at random. The annealing schedule is defined by the call , which should yield the temperature to use, given the fraction of the time budget that has been expended so far.

下面的伪代码展示了上面描述的模拟退火启发式代码。它从一个状态开始，一直持续到采取了最多个步骤。在这个过程中，调用应该产生一个给定状态的随机选择的邻居; 调用应该选择并返回一个范围内的值，均匀地随机。退火时间表是由调用定义的，它应该产生使用的温度，给定的部分时间预算已经花费到目前为止。

35px; width: 600px

Let $s = s 0$

For $k = 0$ through $k max$ (exclusive):

- $T \leftarrow temperature((k+1) / k max)$

- Pick a random neighbour, $s new \leftarrow neighbour(s)$

- If $P (E (s), E (s new), T) \geq random(0, 1)$ :

- - $s \leftarrow s new$

Output: the final state $s$

/ div

参数选择

In order to apply the simulated annealing method to a specific problem, one must specify the following parameters: the state space, the energy (goal) function E(), the candidate generator procedure neighbour(), the acceptance probability function P(), and the annealing schedule temperature() AND initial temperature <init temp>. These choices can have a significant impact on the method's effectiveness. Unfortunately, there are no choices of these parameters that will be good for all problems, and there is no general way to find the best choices for a given problem. The following sections give some general guidelines.

In order to apply the simulated annealing method to a specific problem, one must specify the following parameters: the state space, the energy (goal) function , the candidate generator procedure , the acceptance probability function , and the annealing schedule AND initial temperature <init temp>. These choices can have a significant impact on the method's effectiveness. Unfortunately, there are no choices of these parameters that will be good for all problems, and there is no general way to find the best choices for a given problem. The following sections give some general guidelines.

为了将模拟退火算法应用于具体问题，退火过程由冷却进度表 Cooling Schedule 控制，包括控制参数的初值 t 及其衰减因子Δt 、每个 t 值时的迭代次数L和停止条件S。模拟退火算法必须指定以下参数:状态空间、能量(目标)函数、候选生成器过程、接受概率函数以及退火时刻表和初始温度<init temp>。这些参数的选择能对模拟退火算法的有效性和准确性产生很大的影响。遗憾的是，并没有适用于所有问题的参数选择方法，也没有找到对于给定问题的最佳参数选择的通用方法。下面几节给出一些一般的指导原则。

充分相邻 Sufficiently near neighbour

Simulated annealing may be modeled as a random walk on a search graph, whose vertices are all possible states, and whose edges are the candidate moves. An essential requirement for the neighbour() function is that it must provide a sufficiently short path on this graph from the initial state to any state which may be the global optimum模板:Snd the diameter of the search graph must be small. In the traveling salesman example above, for instance, the search space for n = 20 cities has n! = 2,432,902,008,176,640,000 (2.4 quintillion) states; yet the number of neighbors of each vertex is [math]\displaystyle{ \sum_{k=1}^{n-1} k=\frac{n(n-1)}{2}=190 }[/math] edges, and the diameter of the graph is [math]\displaystyle{ n-1 }[/math].

Simulated annealing may be modeled as a random walk on a search graph, whose vertices are all possible states, and whose edges are the candidate moves. An essential requirement for the function is that it must provide a sufficiently short path on this graph from the initial state to any state which may be the global optimum the diameter of the search graph must be small. In the traveling salesman example above, for instance, the search space for n = 20 cities has n! = 2,432,902,008,176,640,000 (2.4 quintillion) states; yet the number of neighbors of each vertex is [math]\displaystyle{ \sum_{k=1}^{n-1} k=\frac{n(n-1)}{2}=190 }[/math] edges, and the diameter of the graph is [math]\displaystyle{ n-1 }[/math].

模拟退火可以建立成一个搜索图上的随机游动模型，其顶点是所有可能的状态，其边是候选移动。对于函数的一个基本要求是模拟退火必须提供一条足够短的路径，从初始状态所到达的任何状态都可能是全局最优状态，搜索图的直径必须很小。例如，在上面的旅行推销员示例中，n = 20个城市的搜索空间有n!= 2,432,902,008,176,640,000 (2.4 quintillion)个州;然而，每个顶点的邻接数是[math]\displaystyle{ \sum_{k=1}^{n-1} k=\frac{n(n-1)}{2}=190 }[/math]边，图的直径是[math]\displaystyle{ n-1 }[/math]。

跃迁概率 Transition probabilities

To investigate the behavior of simulated annealing on a particular problem, it can be useful to consider the transition probabilities that result from the various design choices made in the implementation of the algorithm. For each edge [math]\displaystyle{ (s,s') }[/math] of the search graph, the transition probability is defined as the probability that the simulated annealing algorithm will move to state [math]\displaystyle{ s' }[/math] when its current state is [math]\displaystyle{ s }[/math]. This probability depends on the current temperature as specified by temperature(), on the order in which the candidate moves are generated by the neighbour() function, and on the acceptance probability function P(). (Note that the transition probability is not simply [math]\displaystyle{ P(e, e', T) }[/math], because the candidates are tested serially.)

To investigate the behavior of simulated annealing on a particular problem, it can be useful to consider the transition probabilities that result from the various design choices made in the implementation of the algorithm. For each edge [math]\displaystyle{ (s,s') }[/math] of the search graph, the transition probability is defined as the probability that the simulated annealing algorithm will move to state [math]\displaystyle{ s' }[/math] when its current state is [math]\displaystyle{ s }[/math]. This probability depends on the current temperature as specified by , on the order in which the candidate moves are generated by the function, and on the acceptance probability function . (Note that the transition probability is not simply [math]\displaystyle{ P(e, e', T) }[/math], because the candidates are tested serially.)

为了研究模拟退火在特定问题上的行为，考虑算法实现过程中的各种设计选择所产生的跃迁概率是很有用的。对于搜索图的每条边[math]\displaystyle{ (s,s') }[/math]，跃迁概率定义为模拟退火算法在当前状态[math]\displaystyle{ s' }[/math] </math> s</math>时移动到状态[math]\displaystyle{ s' }[/math]的概率。此概率取决于指定的当前温度、函数生成候选移动的顺序以及接受概率函数。注意，跃迁概率不是简单地[math]\displaystyle{ P(e, e'， T) }[/math]，因为候选对象是连续进行测试的。

接受概率 Acceptance probabilities

The specification of neighbour(), P(), and temperature() is partially redundant. In practice, it's common to use the same acceptance function P() for many problems, and adjust the other two functions according to the specific problem.

The specification of , , and is partially redundant. In practice, it's common to use the same acceptance function for many problems, and adjust the other two functions according to the specific problem. 和的规范部分是多余的。在实际应用中，对许多问题使用相同的验收函数，并根据具体问题对其他两个函数进行调整，这是很常见的。

In the formulation of the method by Kirkpatrick et al., the acceptance probability function [math]\displaystyle{ P(e, e', T) }[/math] was defined as 1 if [math]\displaystyle{ e' \lt e }[/math], and [math]\displaystyle{ \exp(-(e'-e)/T) }[/math] otherwise. This formula was superficially justified by analogy with the transitions of a physical system; it corresponds to the Metropolis–Hastings algorithm, in the case where T=1 and the proposal distribution of Metropolis–Hastings is symmetric. However, this acceptance probability is often used for simulated annealing even when the neighbour() function, which is analogous to the proposal distribution in Metropolis–Hastings, is not symmetric, or not probabilistic at all. As a result, the transition probabilities of the simulated annealing algorithm do not correspond to the transitions of the analogous physical system, and the long-term distribution of states at a constant temperature [math]\displaystyle{ T }[/math] need not bear any resemblance to the thermodynamic equilibrium distribution over states of that physical system, at any temperature. Nevertheless, most descriptions of simulated annealing assume the original acceptance function, which is probably hard-coded in many implementations of SA.

In the formulation of the method by Kirkpatrick et al., the acceptance probability function [math]\displaystyle{ P(e, e', T) }[/math] was defined as 1 if [math]\displaystyle{ e' \lt e }[/math], and [math]\displaystyle{ \exp(-(e'-e)/T) }[/math] otherwise. This formula was superficially justified by analogy with the transitions of a physical system; it corresponds to the Metropolis–Hastings algorithm, in the case where T=1 and the proposal distribution of Metropolis–Hastings is symmetric. However, this acceptance probability is often used for simulated annealing even when the function, which is analogous to the proposal distribution in Metropolis–Hastings, is not symmetric, or not probabilistic at all. As a result, the transition probabilities of the simulated annealing algorithm do not correspond to the transitions of the analogous physical system, and the long-term distribution of states at a constant temperature [math]\displaystyle{ T }[/math] need not bear any resemblance to the thermodynamic equilibrium distribution over states of that physical system, at any temperature. Nevertheless, most descriptions of simulated annealing assume the original acceptance function, which is probably hard-coded in many implementations of SA.

在Kirkpatrick等人的方法中，如果[math]\displaystyle{ e' \lt e }[/math]， [math]\displaystyle{ \exp(-(e'-e)/T) }[/math]，则接受概率函数[math]\displaystyle{ P(e, e'， T) }[/math]定义为1。这一公式实际上是通过类比物理系统的变迁而得到证明的;在T=1且建议分布对称的情况下，对应于Metropolis-Hastings算法。然而，这个接受概率经常被用于模拟退火算法，甚至当函数(类似于Metropolis-Hastings中的建议分布)不是对称的，或者根本不是概率性的时候也是如此。因此，模拟退火算法的跃迁概率并不对应于类似物理系统的跃迁概率，并且，在恒温[math]\displaystyle{ T }[/math]状态下的长期分布与物理系统在任何温度下状态上的热力学平衡分布并不相似。然而，大多数关于模拟退火的描述都假定了最初的接受函数，这使得可能在SA的许多实现中都是硬编码 hard-coded的。硬编码指“将可变变量用一个固定数值表示”，这种方式在编码的过程中会导致变量很难修改。

In 1990, Moscato and Fontanari ^[7], and independently Dueck and Scheuer ^[8], proposed that a deterministic update (i.e. one that is not based on the probabilistic acceptance rule) could speed-up the optimization process without impacting on the final quality. Moscato and Fontanari conclude from observing the analogous of the "specific heat" curve of the "threshold updating" annealing originating from their study that "the stochasticity of the Metropolis updating in the simulated annealing algorithm does not play a major role in the search of near-optimal minima". Instead, they proposed that "the smoothening of the cost function landscape at high temperature and the gradual definition of the minima during the cooling process are the fundamental ingredients for the success of simulated annealing." The method subsequently popularized under the denomination of "threshold accepting" due to Dueck and Scheuer's denomination. In 2001, Franz, Hoffmann and Salamon showed that the deterministic update strategy is indeed the optimal one within the large class of algorithms that simulate a random walk on the cost/energy landscape ^[9].

In 1990, Moscato and Fontanari^[10], proposed that a deterministic update (i.e. one that is not based on the probabilistic acceptance rule) could speed-up the optimization process without impacting on the final quality. Moscato and Fontanari conclude from observing the analogous of the "specific heat" curve of the "threshold updating" annealing originating from their study that "the stochasticity of the Metropolis updating in the simulated annealing algorithm does not play a major role in the search of near-optimal minima". Instead, they proposed that "the smoothening of the cost function landscape at high temperature and the gradual definition of the minima during the cooling process are the fundamental ingredients for the success of simulated annealing." The method subsequently popularized under the denomination of "threshold accepting" due to Dueck and Scheuer's denomination. In 2001, Franz, Hoffmann and Salamon showed that the deterministic update strategy is indeed the optimal one within the large class of algorithms that simulate a random walk on the cost/energy landscape . 1990年，莫斯卡托 Moscato 和丰塔纳里 Fontanari^[11]提出确定性更新(即不基于概率接受规则的更新)，其可以在不影响最终质量的情况下加快优化过程。 Moscato和Fontanari通过观察源自他们的研究的类似于“阈值更新”退火的“比热”曲线得出结论：“模拟退火算法中的Metropolis更新的随机性在寻找近似最优最小值中没有发挥主要作用”。相反，他们提出“在高温下平滑成本函数景观和在冷却过程中逐渐定义最小值是模拟退火成功的基本要素。” 这种方法后来被Dueck和Scheuer命名为“阈值接受”而推广开来。在2001年，Franz, Hoffmann和Salamon证明了确定性更新策略确实是在模拟成本/能量趋势图上随机行走的大类算法中最优的。

 ---~~energy landscape 能量绘景，能量图景，能源景观，能量景貌  译为能量图？能量趋势图

有效的备选 Efficient candidate generation

When choosing the candidate generator neighbour(), one must consider that after a few iterations of the simulated annealing algorithm, the current state is expected to have much lower energy than a random state. Therefore, as a general rule, one should skew the generator towards candidate moves where the energy of the destination state [math]\displaystyle{ s' }[/math] is likely to be similar to that of the current state. This heuristic (which is the main principle of the Metropolis–Hastings algorithm) tends to exclude "very good" candidate moves as well as "very bad" ones; however, the former are usually much less common than the latter, so the heuristic is generally quite effective.

When choosing the candidate generator , one must consider that after a few iterations of the simulated annealing algorithm, the current state is expected to have much lower energy than a random state. Therefore, as a general rule, one should skew the generator towards candidate moves where the energy of the destination state [math]\displaystyle{ s' }[/math] is likely to be similar to that of the current state. This heuristic (which is the main principle of the Metropolis–Hastings algorithm) tends to exclude "very good" candidate moves as well as "very bad" ones; however, the former are usually much less common than the latter, so the heuristic is generally quite effective.

在选择候选产生器时，必须考虑到经过模拟退火算法的多次迭代后，当前状态的能量比随机状态低得多。因此，通常的规则是，当目标状态[math]\displaystyle{ s' }[/math]的能量可能与当前状态类似时，应该使生成器向候选的地方移动倾斜。这种启发式(这是Metropolis-Hastings算法的主要原则)倾向于排除“非常好的”候选移动和“非常糟糕的”候选移动; 然而，前者通常比后者少得多，所以启发式通常是相当有效的。

In the traveling salesman problem above, for example, swapping two consecutive cities in a low-energy tour is expected to have a modest effect on its energy (length); whereas swapping two arbitrary cities is far more likely to increase its length than to decrease it. Thus, the consecutive-swap neighbour generator is expected to perform better than the arbitrary-swap one, even though the latter could provide a somewhat shorter path to the optimum (with [math]\displaystyle{ n-1 }[/math] swaps, instead of [math]\displaystyle{ n(n-1)/2 }[/math]).

In the traveling salesman problem above, for example, swapping two consecutive cities in a low-energy tour is expected to have a modest effect on its energy (length); whereas swapping two arbitrary cities is far more likely to increase its length than to decrease it. Thus, the consecutive-swap neighbour generator is expected to perform better than the arbitrary-swap one, even though the latter could provide a somewhat shorter path to the optimum (with [math]\displaystyle{ n-1 }[/math] swaps, instead of [math]\displaystyle{ n(n-1)/2 }[/math]).

例如，在上面的旅行商问题中，也就是TSP问题（Traveling Salesman Problem）。假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。在一个寻找最短路径的旅行中，对两个连续的城市所走的顺序进行交换，预计会对其能量(长度)产生适度的影响;而交换两个任意的城市的移动顺序更有可能增加而不是减少城市的长度。因此，预期连续交换邻接生成器的性能要优于任意交换生成器，尽管后者可以提供更短的路径来达到最佳状态(使用[math]\displaystyle{ n-1 }[/math]交换，而不是[math]\displaystyle{ n(n-1)/2 }[/math])。

A more precise statement of the heuristic is that one should try first candidate states [math]\displaystyle{ s' }[/math] for which [math]\displaystyle{ P(E(s), E(s'), T) }[/math] is large. For the "standard" acceptance function [math]\displaystyle{ P }[/math] above, it means that [math]\displaystyle{ E(s') - E(s) }[/math] is on the order of [math]\displaystyle{ T }[/math] or less. Thus, in the traveling salesman example above, one could use a neighbour() function that swaps two random cities, where the probability of choosing a city-pair vanishes as their distance increases beyond [math]\displaystyle{ T }[/math].

A more precise statement of the heuristic is that one should try first candidate states [math]\displaystyle{ s' }[/math] for which [math]\displaystyle{ P(E(s), E(s'), T) }[/math] is large. For the "standard" acceptance function [math]\displaystyle{ P }[/math] above, it means that [math]\displaystyle{ E(s') - E(s) }[/math] is on the order of [math]\displaystyle{ T }[/math] or less. Thus, in the traveling salesman example above, one could use a function that swaps two random cities, where the probability of choosing a city-pair vanishes as their distance increases beyond [math]\displaystyle{ T }[/math].

关于这种启发式的一个更精确的陈述是，人们应该尝试第一个候选状态的数学 s / math，对于这个状态的数学 p (e (s) ，e (s’) ，t) / math 是很大的。对于上面提到的“标准”接受函数数学 p / math，它意味着数学 e (s’)-e (s) / math 的顺序是数学 t / math 或更少。因此，在上面的旅行推销员的例子中，我们可以使用一个交换两个随机城市的函数，其中选择一个城市对的概率消失了，因为它们的距离增加超过了数学 t / math。

一个更精确的启发式陈述是，我们应该尝试第一个候选状态[math]\displaystyle{ s' }[/math]，其中[math]\displaystyle{ P(E(s)， E(s')， T) }[/math]很大。对于上面的“标准”接受函数[math]\displaystyle{ P }[/math]，这意味着[math]\displaystyle{ E(s') - E(s) }[/math]的长度是[math]\displaystyle{ T }[/math]或更少。因此，在上面的旅行商问题中，我们可以使用一个函数来交换两个随机城市，当它们的距离超过[math]\displaystyle{ T }[/math]时，就不再选择该城市对。

避开障碍Barrier avoidance

When choosing the candidate generator neighbour() one must also try to reduce the number of "deep" local minima—states (or sets of connected states) that have much lower energy than all its neighbouring states. Such "closed catchment basins" of the energy function may trap the simulated annealing algorithm with high probability (roughly proportional to the number of states in the basin) and for a very long time (roughly exponential on the energy difference between the surrounding states and the bottom of the basin).

When choosing the candidate generator one must also try to reduce the number of "deep" local minima—states (or sets of connected states) that have much lower energy than all its neighbouring states. Such "closed catchment basins" of the energy function may trap the simulated annealing algorithm with high probability (roughly proportional to the number of states in the basin) and for a very long time (roughly exponential on the energy difference between the surrounding states and the bottom of the basin).

在选择候选生成器时，还必须尝试减少具有比所有相邻状态低得多的能量的“深层”局部最小状态(或连接状态集)的数量。这种能量函数的“封闭集水盆地”可能以很高的概率(大致与盆地内的状态数成正比)并在很长一段时间内(大致以指数形式反映周围状态与盆地底部的能量差)困住模拟退火算法。

 --~~这句话我有些不太理解 只能先直译一下，感觉有些像说 盆地是指较优点，会困住模拟退火算法

As a rule, it is impossible to design a candidate generator that will satisfy this goal and also prioritize candidates with similar energy. On the other hand, one can often vastly improve the efficiency of simulated annealing by relatively simple changes to the generator. In the traveling salesman problem, for instance, it is not hard to exhibit two tours [math]\displaystyle{ A }[/math], [math]\displaystyle{ B }[/math], with nearly equal lengths, such that (1) [math]\displaystyle{ A }[/math] is optimal, (2) every sequence of city-pair swaps that converts [math]\displaystyle{ A }[/math] to [math]\displaystyle{ B }[/math] goes through tours that are much longer than both, and (3) [math]\displaystyle{ A }[/math] can be transformed into [math]\displaystyle{ B }[/math] by flipping (reversing the order of) a set of consecutive cities. In this example, [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] lie in different "deep basins" if the generator performs only random pair-swaps; but they will be in the same basin if the generator performs random segment-flips.

一般来说，不可能设计一个候选生成器，既能满足这个目标，又能优先考虑具有类似能量的候选人。另一方面，人们通常可以通过对生成器进行相对简单的改变来大大提高模拟退火的效率。例如，在旅行推销员问题中，不难发现两个长度几乎相等的旅行数学 a / 数学 b / 数学，比如(1)数学 a / 数学是最优的; (2)每一个将数学 a / 数学转换为数学 b / 数学的城市对交换序列都要经过比两者都长得多的旅行; (3)数学 a / 数学可以通过翻转一组连续的城市转换为数学 b / 数学。在这个例子中，如果生成器只进行随机对偶交换，数学 a / math 和数学 b / math 位于不同的“深盆”中; 但是如果生成器执行随机分段翻转，它们将位于同一盆中。通常，不可能设计一个候选生成器来满足这个目标，并且优先考虑具有相同能量的候选。一般来说，不可能设计一个候选生成器，既能满足这个目标，又能优先考虑具有类似能量的候选移动。另一方面，通过对生成器进行相对简单的更改，可以极大地提高模拟退火的效率。例如在旅行商问题中，不难看出旅行[math]\displaystyle{ A }[/math], [math]\displaystyle{ B }[/math]有着近似相等的长度（1）[math]\displaystyle{ A }[/math]处最优；（2）从[math]\displaystyle{ A }[/math]到[math]\displaystyle{ B }[/math]的每个城市对相互转换，经过更长的旅程

(3) 通过翻转(颠倒顺序)一系列连续的城市[math]\displaystyle{ A }[/math]可以转换成[math]\displaystyle{ B }[/math]。

在这个例子中，如果生成器只执行随机的对交换，[math]\displaystyle{ A }[/math]和[math]\displaystyle{ B }[/math]位于不同的“深盆”中;但是，如果生成器执行随机段翻转，它们将处于相同的池中。

冷却时刻表Cooling schedule

The physical analogy that is used to justify simulated annealing assumes that the cooling rate is low enough for the probability distribution of the current state to be near thermodynamic equilibrium at all times. Unfortunately, the relaxation time—the time one must wait for the equilibrium to be restored after a change in temperature—strongly depends on the "topography" of the energy function and on the current temperature. In the simulated annealing algorithm, the relaxation time also depends on the candidate generator, in a very complicated way. Note that all these parameters are usually provided as black box functions to the simulated annealing algorithm. Therefore, the ideal cooling rate cannot be determined beforehand, and should be empirically adjusted for each problem. Adaptive simulated annealing algorithms address this problem by connecting the cooling schedule to the search progress. Other adaptive approach as Thermodynamic Simulated Annealing^[12], automatically adjusts the temperature at each step based on the energy difference between the two states, according to the laws of thermodynamics.

The physical analogy that is used to justify simulated annealing assumes that the cooling rate is low enough for the probability distribution of the current state to be near thermodynamic equilibrium at all times. Unfortunately, the relaxation time—the time one must wait for the equilibrium to be restored after a change in temperature—strongly depends on the "topography" of the energy function and on the current temperature. In the simulated annealing algorithm, the relaxation time also depends on the candidate generator, in a very complicated way. Note that all these parameters are usually provided as black box functions to the simulated annealing algorithm. Therefore, the ideal cooling rate cannot be determined beforehand, and should be empirically adjusted for each problem. Adaptive simulated annealing algorithms address this problem by connecting the cooling schedule to the search progress. Other adaptive approach as Thermodynamic Simulated Annealing, automatically adjusts the temperature at each step based on the energy difference between the two states, according to the laws of thermodynamics.

用来证明模拟退火合理性的物理类比是假定冷却速率足够低，使当前状态的概率分布在任何时候都接近热力学平衡。遗憾的是，弛豫时间——一个人必须等待平衡在温度变化后恢复的时间——强烈地依赖于能量函数的“地形”和当前的温度。在模拟退火算法中，弛豫时间也以非常复杂的方式依赖于候选生成器。注意，所有这些参数通常都作为黑盒函数提供给模拟退火算法。因此，理想的冷却速率不能预先确定，应该根据实际情况对每个问题进行调整。自适应模拟退火算法通过将冷却计划与搜索过程相结合来解决这个问题。其他自适应方法如热力模拟退火，根据美国热力学定律协会的说法，可以根据两种状态之间的能量差自动调节每一步的温度。

Restarts

Sometimes it is better to move back to a solution that was significantly better rather than always moving from the current state. This process is called restarting of simulated annealing. To do this we set s and e to sbest and ebest and perhaps restart the annealing schedule. The decision to restart could be based on several criteria. Notable among these include restarting based on a fixed number of steps, based on whether the current energy is too high compared to the best energy obtained so far, restarting randomly, etc.

Sometimes it is better to move back to a solution that was significantly better rather than always moving from the current state. This process is called restarting of simulated annealing. To do this we set s and e to sbest and ebest and perhaps restart the annealing schedule. The decision to restart could be based on several criteria. Notable among these include restarting based on a fixed number of steps, based on whether the current energy is too high compared to the best energy obtained so far, restarting randomly, etc.

有时候，回到一个比总是从当前状态移动更好的解决方案，而不是总是从当前状态移动。这个过程被称为模拟退火的重新启动。为此，我们将s和e 设置为sbest和ebest并可能重新启动退火时刻表。重新启动的决定可能基于几个标准。其中值得注意的有:基于固定步数的重启，基于当前能量是否高于目前获得的最佳能量，随机重启等。

Related methods

Interacting Metropolis–Hasting algorithms (a.k.a. Sequential Monte Carlo^[13]) combined simulated annealing moves with an acceptance-rejection of the best fitted individuals equipped with an interacting recycling mechanism.

Quantum annealing uses "quantum fluctuations" instead of thermal fluctuations to get through high but thin barriers in the target function.

Stochastic tunneling attempts to overcome the increasing difficulty simulated annealing runs have in escaping from local minima as the temperature decreases, by 'tunneling' through barriers.

Tabu search normally moves to neighbouring states of lower energy, but will take uphill moves when it finds itself stuck in a local minimum; and avoids cycles by keeping a "taboo list" of solutions already seen.

Dual-phase evolution is a family of algorithms and processes (to which simulated annealing belongs) that mediate between local and global search by exploiting phase changes in the search space.

Reactive search optimization focuses on combining machine learning with optimization, by adding an internal feedback loop to self-tune the free parameters of an algorithm to the characteristics of the problem, of the instance, and of the local situation around the current solution.

Stochastic gradient descent runs many greedy searches from random initial locations.

Genetic algorithms maintain a pool of solutions rather than just one. New candidate solutions are generated not only by "mutation" (as in SA), but also by "recombination" of two solutions from the pool. Probabilistic criteria, similar to those used in SA, are used to select the candidates for mutation or combination, and for discarding excess solutions from the pool.

Memetic algorithms search for solutions by employing a set of agents that both cooperate and compete in the process; sometimes the agents' strategies involve simulated annealing procedures for obtaining high quality solutions before recombining them.^[14] Annealing has also been suggested as a mechanism for increasing the diversity of the search ^[15].

Graduated optimization digressively "smooths" the target function while optimizing.

Ant colony optimization (ACO) uses many ants (or agents) to traverse the solution space and find locally productive areas.

The cross-entropy method (CE) generates candidates solutions via a parameterized probability distribution. The parameters are updated via cross-entropy minimization, so as to generate better samples in the next iteration.

Harmony search mimics musicians in improvisation process where each musician plays a note for finding a best harmony all together.

Stochastic optimization is an umbrella set of methods that includes simulated annealing and numerous other approaches.

Particle swarm optimization is an algorithm modelled on swarm intelligence that finds a solution to an optimization problem in a search space, or model and predict social behavior in the presence of objectives.

The runner-root algorithm (RRA) is a meta-heuristic optimization algorithm for solving unimodal and multimodal problems inspired by the runners and roots of plants in nature.

Intelligent water drops algorithm (IWD) which mimics the behavior of natural water drops to solve optimization problems

Parallel tempering is a simulation of model copies at different temperatures (or Hamiltonians) to overcome the potential barriers.

Interacting Metropolis–Hasting algorithms (a.k.a. Sequential Monte Carlo[12]) combined simulated annealing moves with an acceptance-rejection of the best fitted individuals equipped with an interacting recycling mechanism.
Quantum annealing uses "quantum fluctuations" instead of thermal fluctuations to get through high but thin barriers in the target function.
Stochastic tunneling attempts to overcome the increasing difficulty simulated annealing runs have in escaping from local minima as the temperature decreases, by 'tunneling' through barriers.
Tabu search normally moves to neighbouring states of lower energy, but will take uphill moves when it finds itself stuck in a local minimum; and avoids cycles by keeping a "taboo list" of solutions already seen.
Dual-phase evolution is a family of algorithms and processes (to which simulated annealing belongs) that mediate between local and global search by exploiting phase changes in the search space.

交互Metropolis–Hasting算法(又名顺序蒙特卡罗[12]算法)结合模拟退火算法，采用交互循环机制，对最适合的个体进行接受-拒绝。
量子退火使用“量子涨落”而不是热涨落来穿过目标函数中高而薄的屏障。
随机隧穿尝试克服模拟退火运行在温度降低时从局部极小值逃逸的困难，通过“隧穿”通过障碍。
禁忌搜索通常会移动到能量较低的邻近状态，但当它发现自己陷入局部极小值时，就会向上移动;并通过保留已经看到的解决方案的“禁忌列表”来避免循环。
双阶段进化是一系列的算法和进程(模拟退火所属)，它们通过利用搜索空间中的相位变化在局部搜索和全局搜索之间进行协调。

Reactive search optimization focuses on combining machine learning with optimization, by adding an internal feedback loop to self-tune the free parameters of an algorithm to the characteristics of the problem, of the instance, and of the local situation around the current solution.
Stochastic gradient descent runs many greedy searches from random initial locations.
Genetic algorithms maintain a pool of solutions rather than just one. New candidate solutions are generated not only by "mutation" (as in SA), but also by "recombination" of two solutions from the pool. Probabilistic criteria, similar to those used in SA, are used to select the candidates for mutation or combination, and for discarding excess solutions from the pool.
Memetic algorithms search for solutions by employing a set of agents that both cooperate and compete in the process; sometimes the agents' strategies involve simulated annealing procedures for obtaining high quality solutions before recombining them.[13] Annealing has also been suggested as a mechanism for increasing the diversity of the search [14].

反应式搜索引擎优化的重点是将机器学习和优化结合起来，通过增加一个内部反馈回路来自动调整算法的自由参数，使其适应问题、实例和当前解决方案周围的局部情况的特点。随机梯度下降从随机的初始位置运行许多贪婪的搜索。

新的候选解决方案不仅产生“变异”(如在 SA) ，而且还“重组”的两个解决方案从池。
有时代理人的策略涉及在重组之前获得高质量解决方案的模拟退火。 退火也被认为是增加搜索多样性的一种机制[14]。

反应式搜索优化侧重于将机器学习与优化结合起来，通过添加一个内部反馈回路，自调整算法的自由参数，根据问题、实例，去适应当前解决方案周围的局部情况。
随机梯度下降法从随机初始点开始进行许多贪婪搜索。
遗传算法保持了一个解决方案池，而不仅仅是一个。
新的候选解决方案不仅可以通过“突变”(如SA)生成，还可以通过从池中“重新组合”两个解决方案生成。与 SA 中使用的概率标准类似，用于选择突变或组合的候选方案，并从池中剔除多余的解。
模因算法通过雇佣一组在过程中既合作又竞争的代理人来寻找解决方案;
有时，代理商的策略包括模拟退火程序，以获得高质量的解决方案，再进行重新组合。[13]模拟退火也被认为是一种增加搜索[14]多样性的机制。

Graduated optimization digressively "smooths" the target function while optimizing.
Ant colony optimization (ACO) uses many ants (or agents) to traverse the solution space and find locally productive areas.
The cross-entropy method (CE) generates candidates solutions via a parameterized probability distribution. The parameters are updated via cross-entropy minimization, so as to generate better samples in the next iteration.
Harmony search mimics musicians in improvisation process where each musician plays a note for finding a best harmony all together.
Stochastic optimization is an umbrella set of methods that includes simulated annealing and numerous other approaches.
逐步优化就是在优化时对目标函数进行“平滑”处理。
蚁群优化(ACO)使用许多蚂蚁(或代理)遍历解空间，寻找局部生产区域。
交叉熵方法(CE)通过参数化的概率分布生成候选解。通过交叉熵最小化对参数进行更新，以便在下一次迭代中生成更好的样本。
和声搜索模仿音乐家在即兴创作的过程中，每个音乐家演奏一个音符以找到最好的和声。
随机优化是一系列包括模拟退火和许多其他方法的算法集合。

Particle swarm optimization is an algorithm modelled on swarm intelligence that finds a solution to an optimization problem in a search space, or model and predict social behavior in the presence of objectives.
The runner-root algorithm (RRA) is a meta-heuristic optimization algorithm for solving unimodal and multimodal problems inspired by the runners and roots of plants in nature.
Intelligent water drops algorithm (IWD) which mimics the behavior of natural water drops to solve optimization problems
Parallel tempering is a simulation of model copies at different temperatures (or Hamiltonians) to overcome the potential barriers.

粒子群优化是一种以群体智能为模型的算法，它可以在搜索空间中找到优化问题的解决方案，或者在目标存在的情况下对社会行为进行建模和预测。
分枝根算法(RRA)是一种元启发式优化算法，用于解决单峰和多峰问题的启发，在自然植物的运行和根。
智能水滴算法(IWD)模仿自然水滴的行为来解决优化问题。
并行退火是模拟模型副本在不同温度(或汉密尔顿)下克服潜在障碍的过程。

另请参阅

自适应模拟退火
马尔可夫链
组合优化
双相演化
自动标签位置
多学科优化
地点和路线
分子动力学
旅行商问题
计算机视觉中的图形切割
粒子群优化
智能水滴算法

References

↑ ^1.0 ^1.1 Kirkpatrick, S.; Gelatt Jr, C. D.; Vecchi, M. P. (1983). "Optimization by Simulated Annealing". Science. 220 (4598): 671–680. Bibcode:1983Sci...220..671K. CiteSeerX 10.1.1.123.7607. doi:10.1126/science.220.4598.671. JSTOR 1690046. PMID 17813860.
↑ Khachaturyan, A.; Semenovskaya, S.; Vainshtein, B. (1979). "Statistical-Thermodynamic Approach to Determination of Structure Amplitude Phases". Sov.Phys. Crystallography. 24 (5): 519–524.
↑ Khachaturyan, A.; Semenovskaya, S.; Vainshtein, B. (1981). "The Thermodynamic Approach to the Structure Analysis of Crystals". Acta Crystallographica. 37 (A37): 742–754. Bibcode:1981AcCrA..37..742K. doi:10.1107/S0567739481001630.
↑ Černý, V. (1985). "Thermodynamical approach to the traveling salesman problem: An efficient simulation algorithm". Journal of Optimization Theory and Applications. 45: 41–51. doi:10.1007/BF00940812.
↑ Metropolis, Nicholas; Rosenbluth, Arianna W.; Rosenbluth, Marshall N.; Teller, Augusta H.; Teller, Edward (1953). "Equation of State Calculations by Fast Computing Machines". The Journal of Chemical Physics. 21 (6): 1087. Bibcode:1953JChPh..21.1087M. doi:10.1063/1.1699114.
↑ Granville, V.; Krivanek, M.; Rasson, J.-P. (1994). "Simulated annealing: A proof of convergence". IEEE Transactions on Pattern Analysis and Machine Intelligence. 16 (6): 652–656. doi:10.1109/34.295910.
↑ Moscato, P.; Fontanari, J.F. (1990), "Stochastic versus deterministic update in simulated annealing", Physics Letters A, 146 (4): 204–208, doi:10.1016/0375-9601(90)90166-L
↑ Dueck, G.; Scheuer, T. (1990), "Threshold accepting: A general purpose optimization algorithm appearing superior to simulated annealing", Journal of Computational Physics, 90 (1): 161–175, doi:10.1016/0021-9991(90)90201-B, ISSN 0021-9991
↑ Franz, A.; Hoffmann, K.H.; Salamon, P, "Best optimal strategy for finding ground states", Physical Review Letters, 86 (3): 5219–5222, doi:10.1103/PhysRevLett.86.5219
↑ Dueck, G.; Scheuer, T. (1990), "Threshold accepting: A general purpose optimization algorithm appearing superior to simulated annealing", Journal of Computational Physics, 90 (1): 161–175, doi:10.1016/0021-9991(90)90201-B, ISSN 0021-9991
↑ Dueck, G.; Scheuer, T. (1990), "Threshold accepting: A general purpose optimization algorithm appearing superior to simulated annealing", Journal of Computational Physics, 90 (1): 161–175, doi:10.1016/0021-9991(90)90201-B, ISSN 0021-9991
↑ De Vicente, Juan; Lanchares, Juan; Hermida, Román (2003). "Placement by thermodynamic simulated annealing". Physics Letters A. 317 (5–6): 415–423. Bibcode:2003PhLA..317..415D. doi:10.1016/j.physleta.2003.08.070.
↑ Del Moral, Pierre; Doucet, Arnaud; Jasra, Ajay (2006). "Sequential Monte Carlo samplers - P. Del Moral - A. Doucet - A. Jasra - 2006 - Journal of the Royal Statistical Society: Series B (Statistical Methodology) - Wiley Online Library". Journal of the Royal Statistical Society, Series B. 68 (3): 411–436. arXiv:cond-mat/0212648. doi:10.1111/j.1467-9868.2006.00553.x.
↑ Moscato, Pablo (June 1993). "An introduction to population approaches for optimization and hierarchical objective functions: A discussion on the role of tabu search". Annals of Operations Research. 41 (2): 85–121. doi:10.1007/BF02022564.
↑ Moscato, P. (1989). "On Evolution, Search, Optimization, Genetic Algorithms and Martial Arts: Towards Memetic Algorithms". Caltech Concurrent Computation Program (report 826).

External links

Simulated Annealing A Javascript app that allows you to experiment with simulated annealing. Source code included.

"General Simulated Annealing Algorithm" An open-source MATLAB program for general simulated annealing exercises.

Self-Guided Lesson on Simulated Annealing A Wikiversity project.

Google in superposition of using, not using quantum computer Ars Technica discusses the possibility that the D-Wave computer being used by Google may, in fact, be an efficient simulated annealing co-processor.

模拟退火的一个Javascript应用程序，允许实验模拟退火。包括源代码。
“通用模拟退火算法”是一个用于通用模拟退火练习的开源MATLAB程序。
模拟退火的自我指导课程维基学院项目。
谷歌在叠加使用、不使用量子计算机的Ars技术中讨论了谷歌所使用的D波计算机可能实际上是一个高效的模拟退火协处理器的可能性。

模板:Major subfields of optimization

Category:Metaheuristics

类别: 启发式元推理

Category:Optimization algorithms and methods

类别: 优化算法和方法

Category:Monte Carlo methods

类别: 蒙特卡罗方法

This page was moved from wikipedia:en:Simulated annealing. Its edit history can be viewed at 模拟退火/edithistory

[:2-1] 1.0 ^1.1 Kirkpatrick, S.; Gelatt Jr, C. D.; Vecchi, M. P. (1983). "Optimization by Simulated Annealing". Science. 220 (4598): 671–680. Bibcode:1983Sci...220..671K. CiteSeerX 10.1.1.123.7607. doi:10.1126/science.220.4598.671. JSTOR 1690046. PMID 17813860.

[:0-2] Khachaturyan, A.; Semenovskaya, S.; Vainshtein, B. (1979). "Statistical-Thermodynamic Approach to Determination of Structure Amplitude Phases". Sov.Phys. Crystallography. 24 (5): 519–524.

[:1-3] Khachaturyan, A.; Semenovskaya, S.; Vainshtein, B. (1981). "The Thermodynamic Approach to the Structure Analysis of Crystals". Acta Crystallographica. 37 (A37): 742–754. Bibcode:1981AcCrA..37..742K. doi:10.1107/S0567739481001630.

[4] Černý, V. (1985). "Thermodynamical approach to the traveling salesman problem: An efficient simulation algorithm". Journal of Optimization Theory and Applications. 45: 41–51. doi:10.1007/BF00940812.

[5] Metropolis, Nicholas; Rosenbluth, Arianna W.; Rosenbluth, Marshall N.; Teller, Augusta H.; Teller, Edward (1953). "Equation of State Calculations by Fast Computing Machines". The Journal of Chemical Physics. 21 (6): 1087. Bibcode:1953JChPh..21.1087M. doi:10.1063/1.1699114.

[6] Granville, V.; Krivanek, M.; Rasson, J.-P. (1994). "Simulated annealing: A proof of convergence". IEEE Transactions on Pattern Analysis and Machine Intelligence. 16 (6): 652–656. doi:10.1109/34.295910.

[7] Moscato, P.; Fontanari, J.F. (1990), "Stochastic versus deterministic update in simulated annealing", Physics Letters A, 146 (4): 204–208, doi:10.1016/0375-9601(90)90166-L

[8] Dueck, G.; Scheuer, T. (1990), "Threshold accepting: A general purpose optimization algorithm appearing superior to simulated annealing", Journal of Computational Physics, 90 (1): 161–175, doi:10.1016/0021-9991(90)90201-B, ISSN 0021-9991

[9] Franz, A.; Hoffmann, K.H.; Salamon, P, "Best optimal strategy for finding ground states", Physical Review Letters, 86 (3): 5219–5222, doi:10.1103/PhysRevLett.86.5219

[10] Dueck, G.; Scheuer, T. (1990), "Threshold accepting: A general purpose optimization algorithm appearing superior to simulated annealing", Journal of Computational Physics, 90 (1): 161–175, doi:10.1016/0021-9991(90)90201-B, ISSN 0021-9991

[11] Dueck, G.; Scheuer, T. (1990), "Threshold accepting: A general purpose optimization algorithm appearing superior to simulated annealing", Journal of Computational Physics, 90 (1): 161–175, doi:10.1016/0021-9991(90)90201-B, ISSN 0021-9991

[12] De Vicente, Juan; Lanchares, Juan; Hermida, Román (2003). "Placement by thermodynamic simulated annealing". Physics Letters A. 317 (5–6): 415–423. Bibcode:2003PhLA..317..415D. doi:10.1016/j.physleta.2003.08.070.

[:3-13] Del Moral, Pierre; Doucet, Arnaud; Jasra, Ajay (2006). "Sequential Monte Carlo samplers - P. Del Moral - A. Doucet - A. Jasra - 2006 - Journal of the Royal Statistical Society: Series B (Statistical Methodology) - Wiley Online Library". Journal of the Royal Statistical Society, Series B. 68 (3): 411–436. arXiv:cond-mat/0212648. doi:10.1111/j.1467-9868.2006.00553.x.

[14] Moscato, Pablo (June 1993). "An introduction to population approaches for optimization and hierarchical objective functions: A discussion on the role of tabu search". Annals of Operations Research. 41 (2): 85–121. doi:10.1007/BF02022564.

[martial_arts-15] Moscato, P. (1989). "On Evolution, Search, Optimization, Genetic Algorithms and Martial Arts: Towards Memetic Algorithms". Caltech Concurrent Computation Program (report 826).

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]