诺伯特·维纳 Norbert Wiener

个人信息

类别	信息
出生日期	1894年11月26日
出生地	Columbia, Missouri, 美国
国籍：	美国
母校：	塔夫茨大学，学士学位，1909年美国康奈尔大学，硕士，1911年美国哈佛大学，博士，1913年
死亡：	1964年3月18日(享年69岁)瑞典斯德哥尔摩
研究领域：	控制论、数学
博士生导师：	卡尔·施密特
主要成就：	美国应用数学家，控制论的创始人
代表作品：	《控制论》，《维纳选集》，《维纳数学论文集》，《昔日神童》

1894 年11月26日，诺伯特·维纳 Norbert Wiener出生在美国密苏里州哥伦比亚市的一个犹太人家庭。他是美国著名的数学家和哲学家。他是麻省理工学院 MIT 的数学教授。他是随机过程和噪声过程的先驱，促进了电子工程，电子通讯和控制系统等相关工作的进行。他被认为是控制论的鼻祖，是最早提出所有智能行为都是反馈机制的结果的理论家之一。反馈机制可以用机器模拟，这是迈向现代人工智能发展的重要的早期步骤。

研究领域

维纳一生发表论文240多篇，著作14本，内容涵盖数学、物理、工程、生物和哲学等多个领域。

控制论

20世纪40年代，生理学中内稳态、自动控制中的闭环反馈控制及稳定性、通讯理论中的负反馈放大器、数学中的统计力学和物理学中的继电器、计算机科学的成就等等，对控制论的诞生起了关键的技术准备作用。

20世纪30年代末起，维纳就和A·罗森勃吕特 A. rosenbluet 在哈佛大学医学院组织方法论的讨论会。1943年到1946年, 由维纳和著名科学家约翰·冯·诺依曼 John von Neumann 发起普林斯顿大学的信息与反馈讨论会。

1946到1953年, 上述会议发展成梅西控制论会议.梅西控制论会议的与会者发现在完全不同的领域里，有些概念是相同的：譬如生物体的内稳态和电气工程中机器的稳态都是同一个概念, 可以相类比。这个思想的建立, 意味着人类对生命活动的认识进入一个新阶段。

反馈基本概念在早期的“信息与反馈”会议上就得到了确认和推广，人们开始认识到：人的行动和目的是从神经系统出发进入肌肉, 然后通过感觉再进入神经系统的环形反馈过程。就是说，首次用反馈和闭环回路来代替原先的目的论中的神经生理行为。罗森勃吕特和维纳的1943年后来被称为最早的控制论论文《行动、目的和目的论 Behaviour, purpose and teleology》是控制论萌芽的重要标志,奠定了控制论思想的雏型。其中心思想是：控制行为是一个从原因到目的之间的随机试探和反复调节的曲折过程。这篇哲学文章第一次明确地构思了如何通过反馈来进行科学意义下的控制。也在这个会议上美国MIT教授、梅西控制论会议主席M·麦克洛克 McCulloch 与 W · 皮茨 Pitts 于1943年提出最早的人工神经元模型论文《内在于神经活动中的思想逻辑计算 A logical calculus of the ideas immanent in nervous activity》, 该模型一般简称为M-P神经元模型, 是目前许多神经元模型的基础,被称为神经元的第一个数学模型。 .

梅西控制论会议的与会者认识到, 在不同领域的工作者之间存在着一个实在的共同思想基础，即信息及通讯和反馈在机器和生物体中都存在。信息及通讯作为组织化机制不但对于个体是重要的而且对于集体(社会、经济)也是重要的。与会者发现关于这些问题的文献缺乏统一的表述, 没有任何共同的术语, 甚至没有一个称呼这个新领域的简单名称，这不适宜于这个新领域未来的发展。为了有利于这个新领域未来的发展，维纳在1947年梅西控制论会议上提出以希腊语的“舵手”(κυβερνητηζ, 意指“领航”)借来的词汇“cybernetics”(译为“控制论”)来代表这个新领域。cybernetics 最早可能是由法国物理和数学家安培 André-Marie Ampere 在其著作《科学哲学的尝试 Essai sur la philosophie des sciences》中使用，但维纳用它来概括了信息、通信和控制三个基本理论。由于其含义主要是后者，现在一般就把它翻译和理解为“控制论”。维纳是 Cybernetics 这一学科的创始人，没有之一。

克劳德·艾尔伍德·香农 Claude Elwood Shannon

第二次世界大战开始后，维纳参与了火炮控制研究，进而建立了Cybernetics理论。此外，维纳还参与了克劳德·艾尔伍德·香农 Claude Elwood Shannon信息论的开创工作。维纳从直流电路出发来理解和诠释信息论，把消息看作可测事件的时间序列并用统计方法来处理通信问题，在数学上采取平稳随机过程理论及各种变换技术进行研究。他在信息论方面与克劳德·艾尔伍德·香农 Claude Elwood Shannon并行工作亦时有合作。他们阐明了信息定量化的原理和方法，用“熵”来定义连续信号的信息量，建立了计算信息量的香农-维纳公式。

维纳的开创性工作有力地推动了信息论的创立，并为信息论的应用开辟了广阔的前景。在这个意义上，克劳德·艾尔伍德·香农 Claude Elwood Shannon感概地说：“光荣应归于维纳教授”。维纳阐明了现代系统控制思想和反馈调节原理。

《行动、目的和目的论 Behaviour, purpose and teleology》、《内在于神经活动中的思想逻辑计算 A logical calculus of the ideas immanent in nervous activity》、生物的“内稳态”, 以及维纳在其《控制论》著作中提到的“目的震颠”、“运动共济失调”以及麦克洛克的“神经元模型”等例子都是将研究机器中的控制和通讯的成就应用到生命体,即维纳《控制论》书名副标题所称的“动物”的研究上。当时的控制论的酝酿和形成主要是将机器(人造物理系统)领域的控制与通讯核心理念应用于研究生物(动物)这一领域而产生的。所以维纳在其书名的副标题上确切地反映了这一点。

此后控制论的反馈、内稳态、信息及通讯、适应、智能等核心理念被推广应用到社会(含经济、管理)、认知, 直到生态、环境、资源、气候等控制, 并相应形成各个新分支。可见, 控制论核心理念在新领域的应用、推广推动了其新分支的创立。

尽管维纳开创了Cybernetics，到1945年美国往日本投放了原子弹之后，他却对利用科学技术制作大规模杀伤武器的军事行动深表厌恶，并拒绝了参与曼哈顿计划的邀请以及军方提供的各种研究资助。1947年1月，维纳在《大西洋月刊 The Atlantic Monthly》上正式发表署名文章“A scientist rebels”，呼吁科学家注重科学研究道德并小心考虑自己的科学研究将可能带来的社会后果。

维纳在1948年出版的书《控制论——或关于在动物和机器中控制和通信的科学 Cybernetics: or Control and Communication in the Animal and the Machine》 中提出和综合了控制论中的几个最基本的概念和方法,如反馈、稳定和镇定，并倡导了对机器和社会之间的通信与控制的研究,人们普遍认为这本书标志了现代意义下的控制科学理论的诞生。

有意思的是，维纳在上述《控制论》一书中说道：“莱布尼茨以后，似乎再没有一个人能够充分地掌握当代的全部知识了。从那时起，科学日益成为专家们愈来愈狭窄领域内进行的事业。”

在上一世纪，也许再没有莱布尼茨那样的人，但还有一个高斯、一个法拉第、一个达尔文。今天没有几个学者可以不加任何限定地自称为数学家，或者物理学家，或者生物学家。一个人只可以是一个拓扑学家，或者一个声学家，或者一个甲虫学家。满嘴讲着自己领域的行话，他可以知道本身那个领域的各个分支和全部文献。

The Human Use of Human Beings:Cybernetics and Society

然而，这种人往往会把邻近的科学问题看作与己无关，甚至认为如果自己对那种问题发生任何兴趣的话，那是一种不能允许的侵犯人家地盘的行为。这解释了为何维纳有兴趣并致力把信息、通信和控制等不同领域的基本理论揉合在一起，由此创造出一门全新的学科：Cybernetics。

1954年，维纳又出版了另一本书《人有人的用处：控制论与社会 The Human Use of Human Beings:Cybernetics and Society》。书中维纳对控制论的基本刻划是：现代的自动机和人都是由感觉装置、动作装置和信息传递系统所组成的一个复合的机械或生物系统。自动机和人同样都在接收、处理、传递和存贮信息，并利用信息去完成动作以实现与外界的联系和交互。在一个系统的工作过程中，信息传递机制发出控制信号命令动作装置进行工作。动作的结果由感觉装置检测出来并反馈回去与给定信号做比较：如果有偏差，则偏差信号会控制动作装置作出自我调节然后继续工作，直到偏差信号消失为止。维纳描述的这个过程正是今天我们熟知的负反馈自动控制原理。

根据这一理论, 维纳相信一个机械系统完全能够进行运算和记忆。1940年，他开始考虑计算机如何能像大脑一样工作。他发现二者极其相似，于是认为计算机是一个进行信息处理和信息转换的系统：只要这个系统能够得到数据，它就应该能够做人所能做的任何事情。但是，维纳警告说：“计算机作为人类的傀儡有可能变成这样一种机器：它们一但被启动就不再能被关闭，它们还可能代替人类做出各种决定。”推而广之，认为一个不接受负反馈的政治体系最后必将崩溃，并因此强调：“一个社会的生存和发展不应该过份依赖于财富金钱，因为那些东西不提供负反馈。”

维纳方程

以维纳命名的布朗运动的简单数学表达式--维纳方程假定了流体粒子的流速随机波动。

维纳过滤器

在概率论的数学领域里，Wiener sausage是布朗运动在时间t之前的轨迹的一个邻域，它由布朗运动的一个固定距离内的所有点给出。它可以被看作是一个半径固定的圆柱体，其中心线是布朗运动。

在信号处理方面，维纳滤波器是维纳在1940年代提出的一种滤波器，1942年作为机密文件介绍并发表发表出来。它的目的是通过与期望的无噪声信号的估计值比较来减少信号中的噪声量。维纳在麻省理工学院辐射实验室开发了这个滤波器，通过雷达反射来预测德国轰炸机的位置。预测未来是必要的，因为当炮弹到达目标附近时，目标已经移动，并且可能稍微改变了方向。他们甚至模拟了飞行员的肌肉反应，这最终形成了控制论。无人驾驶的 V1引擎特别容易制造，在好天气里，装有维纳滤镜的美国枪支可以在从英吉利海峡进入英国、飞往伦敦的途中击落100架 V1引擎的飞机。这出现了一种具有很大普遍性的数学理论ーー一种基于过去的不完全信息尽可能最好地预测未来的理论。这是一个统计学理论，其中包括的应用，严格来说，并不能预测未来，只是试图去除噪音。它利用了维纳早期关于积分方程和傅里叶变换的工作。

数学

在二维空间通过Lévy飞行1000步后的结果

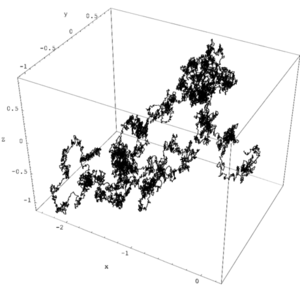
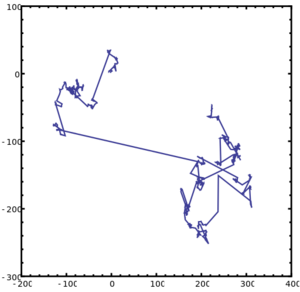
维纳对布朗运动的数学理论(以罗伯特·布朗命名)非常感兴趣，他证明了许多现在广为人知的结果，例如路径的不可微性。因此，布朗运动的一维形式被命名为维纳过程。它是最著名的 Lévy 过程，càdlàg 随机过程具有平稳的统计独立的增量，并经常出现在纯粹的和应用的数学，物理和经济学(例如在股票市场)。

1932年维纳的一个成果，在可和性理论中发展了 taubrian 定理，面对它的一个章节的实分析，大多数已知的结果可以从傅里叶分析中得出。在现有的公式中，Wiener 定理与处理无穷级数的 taubrian 定理没有任何明显的联系。从为积分公式化的结果或者使用泛函分析语言和 Banach 代数的翻译中，只是一个相对常规的过程。

维纳还讨论了整函数在 Cn 上的增长性和紧支集的 Schwartz 分布的 Fourier 变换。

Wiener-Khinchin 定理(也称为 Khinchin-Kolmogorov 定理)指出，广义平稳随机过程的谱密度是相应自相关函数的傅里叶变换。

维纳空间是测度理论中的一个数学对象，用于在无限维向量空间上构造一个“正的”局部有限的测度。维纳的原始构造只适用于实值连续路径空间上的单位区间，称为经典维纳空间。伦纳德·格罗斯 Leonard Gross 对一般可分 Banach 空间的情形作了推广。

Banach 空间的概念本身是由维纳和斯蒂芬·巴纳赫大约在同一时间独立发现的。

傅里叶分析马里兰大学学院市分校数学系诺伯特·维纳中心致力于研究诺伯特·维纳留下的科学和数学遗产。 NWC 网站强调了该中心的研究活动。此外，每年诺伯特维纳中心主办二月傅立叶会谈，一个为期两天的全国会议展示在工业、政府和学术界的纯粹和应用傅里叶分析的进展.

个人经历

1894年11月26日，诺伯特•维纳（Norbert Wiener）出生在美国密苏里州哥伦比亚市的一个犹太人家庭。维纳成名后出版过两部自传，第一本是1953年的《昔日神童》，记述了自己一些童年往事;第二本是 1956 年的《我是一个数学家》，主要说的是他后半生的事情。维纳的母亲 Bertha Kahn 出生于密苏里州，是德国犹太人的后裔，父亲 Leo Wiener 则是俄罗斯和波兰血统的犹太人，自学成才，时任哈佛大学 Slavic 语言学教授。维纳小时候接受的是由父亲一手包办的家庭教育，9 岁时直接进入 Ayer 高中， 12 岁成为 Tufts 学院学生，15 岁获得数学学士学位。年轻的维纳对物理、化学、生物兴趣极高，后来在哈佛大学当了一年动物学研究生，之后因天生眼疾做动物实验经常出错而放弃。随后转到康奈尔 Cornell 大学研修哲学，第二年又回到哈佛攻读数理逻辑，18岁获哈佛大学哲学博士学位。

1913年是青年维纳学术成绩灿烂斐然的一年。他以一篇哲学论文赢得哈佛大学授予 Bowdoin 奖。同年，他向学校申请了旅行奖学金并获得批准，先后留学英国剑桥大学和德国哥廷根大学。他到英国后随即在《剑桥哲学学会会刊》上发表了一篇有关集合论的论文，在数理逻辑学领域被认为具有重要价值。

在剑桥大学，维纳跟随罗素 Bertrand Russell 学习数理逻辑与哲学。罗素成为了维纳的良师益友。老师对他说，一个有志于数理逻辑和哲学的人最好能多懂些数学。秉承师训，维纳选读了许多数学课程，并接受了哈代 G. H. Hardy 和李特尔伍德 John E. Littlewood 等著名数学家的直接指导。维纳原计划在剑桥访学一年，但第二学期罗素要去哈佛讲学，便建议他到德国哥廷根大学去修读希尔伯特 David Hilbert 和朗道 Lev Landau 的课程。在哥廷根大学，维纳修完了朗道的一门代数群论课，并在希尔伯特指导下研究微分方程。在哥廷根所受的教育使维纳受益非浅。

事实上，正是剑桥和哥廷根让神童维纳转变成一名青年数学家。维纳在其后五十多年的科学生涯中，先后涉足哲学、数学、物理学、工程学和生物学，在各个领域中都取得了丰硕成果，成为学识渊博、多才多艺的科学巨匠。回首往事时，他常常感激罗素并十分怀念剑桥与哥廷根。

MIT Building 10 and the Great Dome, Cambridge MA.jpg

第一次世界大战爆发后他从德国返回美国，先后从事过教员、编辑、电话员、专栏作家等多种临时工作，并服过一年后勤兵役。之后，他在哈佛大学求职不果，于1919 年到麻省理工学院 MIT 任职讲师，从此开始了他的学术生涯，并在那里工作和生活直至去世。

1920年，维纳将法国数学家弗雷歇 Fréchet 关于极限和微分的广义理论推广到矢量空间（维纳称之为“差异空间 Differential Space”），并给出了一套完整的公理集合。维纳的结果与波兰数学家巴拿赫 Stefan Banach 几个星期后发表的一篇论文不谋而合。这两项本质上相同的工作后来分别被称为巴拿赫空间和维纳空间理论。维纳的研究成果为约翰·冯·诺依曼 John von Neumann在1927年提出希尔伯特空间中的算子公理方法打下了基础。

维纳是第一个从数学上严格而深刻地研究随机布朗运动的数学家。1921年，他发表了一篇关于布朗运动的重要论文，出发点是函数空间中的测度论。1923年，他第一次给出了随机函数的严格定义，并指出它是布朗运动的理论模型。其后，数学文献上把定义在连续函数空间中的一种描述布朗运动的测度称为维纳测度，相应的随机过程称为维纳过程，在这个测度上的积分称为维纳积分。后来日本数学家伊藤清 Kiyosi Itô 在此基础上发展了随机积分理论。1923-1925年间，维纳对数学上的位势理论作出了重要贡献。他对于给定连续边值函数的Dirichlet问题得出了精确广义解，同时对于一般紧集定义了容度的概念，还给出了著名的正则性判据。因此，维纳大大地扩展了经典的位势理论。

1926年，维纳以Guggenheim（古根海姆）学者身份再次来到德国哥廷根和英国剑桥。随后几年间，他在调和分析的研究上有了重大突破。维纳从物理学借来各种函数作为调和分析的工具，把它们写成Fourier变换（傅里叶变换）的形式，然后把它们同通信理论联系起来，并获得了现代光谱分布。维纳在这方面的成果后来成为巴拿赫代数理论的基石，并由此导出数论Tauber定理等结果。期间，维纳被数学物理深深吸引，与波恩 Max Born 一起研究过量子理论。

1926年，维纳由父母操办与德国姑娘玛格丽特·恩格尔曼 Marguerite Engelmann 结了婚，他们后来有了两个女儿。

1929年，维纳从欧洲回到MIT后晋升为副教授。那是他在MIT任职讲师10年之后。当时学院对这位天才数学家并没有给予特别的关照——但也许正是这无意的举措没有让维纳因青年得志而固步自封—这种悲剧在学术界屡见不鲜。

1929年，维纳还指导当时在贝尔电话公司实习的MIT博士生李郁荣 YukWing Lee 研制了“LeeWiener网络”并获得一项专利。

1932年，维纳与天文学家霍普夫 Eberhard Hopf 合作，把霍普夫关于辐射平衡态的研究推广到一类给定在半无穷区间上带差核的奇异积分方程。此类方程后来被称为维纳-霍普夫方程。

1932年，维纳晋升为教授。翌年，他由于有关Tauber定理的漂亮成果与摩尔斯 Samuel F. B. Morse 分享了美国数学学会五年一次的博修奖 Bôcher奖 ，并当选为美国国家科学院院士。

1936 年维纳与清华大学电机系人员合影:前排左二李郁荣，左三顾毓秀，左四维纳

1935-1936年间，维纳接受了在清华大学电机系任职的李郁荣的建议和推荐，并获得了北京清华大学校长梅贻琦以及数学系主任熊庆来的邀请来到了北京，在清华大学同时出任数学系和电机系的客座教授。期间，他在数学系和李郁荣合作研究Fourier变换数学滤波器，于是后来有了维纳滤波器，这项研究还让他获得了一项发明专利。维纳滤波器是当时线性滤波和预测理论中最为重要的科学成果，成为后来通信理论及其工程应用发展的关键。他又和李郁荣一道与工学院院长、另一名MIT博士海归顾毓琇 YuHsiu Ku 合作，研究模拟计算机的数字化。维纳非常珍惜他在清华的这段经历。他在1954年出版的《我是一个数学家》书中说：他宁愿选择在清华大学任职客座教授的1935年作为他后来创立控制理论的起点，看来他当时在清华已经有了关于控制论的基本构思。

维纳在清华期间还和华罗庚结为好友。1936年，华罗庚获得中华文化教育基金会每年1200美元的乙类资助，可以作为访问学者去英国剑桥大学进修，维纳便亲自写信把华罗庚推荐给了哈代。维纳回国后，又鼓动普林斯顿的约翰·冯·诺依曼 John von Neumann去清华访问。当时约翰·冯·诺依曼 John von Neumann夫妇很感兴趣，于是维纳正式向梅贻琦、熊庆来以及李郁荣分别写了推荐信。可惜两个月后抗日战争爆发，全盘计划化为乌有。

人生侧面

名人传记通常都只有他们成功的记录，往往让后人望而生畏。其实，维纳是天才，但也是凡人；他很成功，但也会失败。

维纳可能是第一个用严格的数学分析方法来研究振动波相位同步理论的科学家，但他采取了一种艰深的Fourier积分方法，最后因找不到解决问题的出路而放弃。

维纳和香农在信息论研究上既合作又竞争。可是与香农相反，在信息论的研究中维纳坚持走模拟而非数字路线，即使用连续而非离散的数学理论和工具，最后没有成功。

在个人生活方面，父亲在维纳小时候发疯一样地要把他培养成神童的各种做法让他内心留下了强烈而持久的抗拒心灵阴影。此外，也许是神童的超常用功让维纳从小就深度近视，在MIT任教期间严重到要摸着墙壁才能走路。他在二战之后更表现出明显的狂躁症状并对同事诉说过有自杀的念头。

弗洛·康韦 Flo Conway 和吉姆·西格尔曼 Jim Siegelman 写的传记《信息时代的黑暗英雄 Dark Hero of the Information Age》提到，生为犹太人的维纳不能容忍妻子对纳粹的热心。特别是，维纳夫人还给丈夫传递了外界关于他们女儿的各种绯闻。痛苦的维纳后来渐渐把自己与同事朋友甚至外界社会隔绝开来，终日独处。他常常拒绝各种荣誉、公众活动甚至学术会议。1953年之后，维纳不再继续自己开创的控制学的研究工作，致使这个学科的成长趋于停顿，直到1960年后的卡尔曼 Rudolf E. Kalman 时代才又重获生机，继续得到蓬勃发展。

博士生

李郁荣 Lee Yuk-wing

Amar Bose

池原止戈夫（博士1930）

多萝西·沃尔科特·怀斯 Dorothy Walcott Weeks（1930年获博士学位）

诺曼·莱文森 Norman Levinson（Sc.D. 1935）

布罗克韦·麦克米兰（博士学位）（1939年）

安倍·格尔巴特（博士学位）1940年

阿玛尔·玻色（1956年毕业）

科林·切里 Colin Cherry（1956年博士）

所获奖项与荣誉

God & Golem

2013年起，IEEE SMC 学会也设立了一个维纳奖

维纳 Wiener 逝世前不久，由约翰逊 Johnson 总统于1964年1月在白宫举行的颁奖典礼上，于1933年获得了博歇纪念奖，并于1963年获得了国家科学奖章。

马里兰大学公园分校的诺伯特·维纳谐波分析和应用中心以他的名字命名。

1987年，美国计算机社会责任专家联盟又设立了诺伯特·维纳社会与专业责任年度奖 Norbert Wiener Award for Social and Professional Responsibility 。

1967年，MIT和美国数学学会以及工业与应用数学学会共同设立了诺伯特·维纳应用数学奖 Norbert Wiener Prize in Applied Mathematics ，每三年颁发一次。

维纳因《上帝与魔像 God & Golem》而获得1965年美国国家科学，哲学和宗教书籍奖：关于控制论影响宗教的某些观点的评论。

1964年1月，维纳由于“在纯粹数学和应用数学方面并且勇于深入到工程和生物科学中去的多种令人惊异的贡献及在这些领域中具有深远意义的开创性工作”荣获美国总统授予的国家科学勋章

维纳曾于1936年在奥斯陆和1950年在马萨诸塞州的剑桥担任ICM的全体发言人。

罗伯特·海因莱因 Robert A. Heinlein 在1957年的小说《银河公民 Citizen of the Galaxy》中以他的名字命名了宇宙飞船，这是第14章中提到的“自由贸易商”船，名为诺伯特·维纳 Norbert Wiener。

特别参考

陈关荣教授的维纳，昔日神童和数学家下为陈关荣教授基本信息：

类别	信息
姓名：	陈关荣（Guanrong Chen）
国籍：	中国
母校：	中山大学
成就：	混沌控制及分岔理论分析与应用
所在机构：	香港城市大学
研究方向：	混沌控制与同步，复杂动态网络，动力学和控制
个人主页链接	陈关荣
所在城市：	中华人民共和国香港特别行政区
联系方式：	(电话)852-3442-7922 (传真)852-3442-0562 (电子邮件)eegchen = cityu-edu-hk

陈关荣教授1981年获广州中山大学计算数学硕士学位，1987年获美国Taxas A&M 大学应用数学博士学位，其后在美国Rice和Houston大学任教。自2000年其，他接受香港城市大学讲座教授职位工作至今，在该校成立了"混沌与复杂网络"学术研究中心并任主任

陈关荣教授于1997年被选为IEEE Fellw, 2008年、 2012年和2016年获国家自然科学二等奖，2011年获俄罗斯圣彼得堡国立大学授予荣誉博士学位和俄罗斯欧拉基金会颁发欧拉金质奖章，2014年获法国诺曼底大学授予荣誉博士学位并当选为欧洲科学院院士，2015年当选为发展中国家科学院院士。

研究工作主要集中在电子工程方面的一个核心领域一非线性系统的控制理论和动力学分析，及其在复杂网络等相关领域中的应用。自1981年以来，共发表了约600篇国际学术杂志论文、250多篇国际学术会议论文、共出版17部研究专著和高等教材，论文他引超过4万次，H指数109，是工程和数学领域高引用研究人员。

进一步阅读

亚马逊：信息时代的黑暗英雄

以诺伯特·维纳命名的事物清单。
蒙塔尼尼，利昂（2017）混乱的和谐。诺伯特·维纳 Norbert Wiener，我们时代的数学家-哲学家。纽约-柏林-海德堡：施普林格。书号 978-3-319-50656-2。
格里克·詹姆斯（2011）信息：历史，理论，洪水纽约：万神殿书。
阿尔米拉 JM（2009）诺伯特·维纳 Norbert Wiener 工程师之间的数学家（西班牙语）马德里：Nivola Libros Y Ediciones Sl书号 978-84-92493-49-4。
Bluma，Lars（2005）诺伯特·维纳 Norbert Wiener 和威斯汀 Kybernetik 在维特 Weltkrieg ：技术史和技术研究（Ph.D.）明斯特。
康威 Flo ，西格曼·吉姆（2005）信息时代的黑暗英雄：寻找控制论之父诺伯特·维纳 Norbert Wiener。纽约：基础书籍。书号 978-0-7382-0368-3。
Grattan-Guinness，Ivor（2000）。寻找数学根源（1870–1940）普林斯顿大学出版社。第290，296，394，395，410，419-422，427，442，528，531，536，538，567 ISBN 978-1400824045。
亚当斯 Colin ；海斯，乔尔；汤普森，阿比盖尔（1998）如何进行Ace微积分：街道指南纽约：WH Freeman and Company。
Heims，Steve J（1993）为战后美国构建社会科学。控制论小组，1946-1953年。麻省理工学院出版社。书号 978-0-262-58123-3。
拜纳姆 Bernum ，特瑞尔·W Terrell W “诺伯特·维纳的愿景：“自动年龄”对我们道德生活的影响” 。
Heims，Steve J（1980）约翰·冯·诺依曼 John von Neumann和诺伯特·维纳 Norbert Wiener ：从数学到生死技术。麻省理工学院出版社。书号 978-0-262-08105-4。
伊格斯 Ilgauds ，汉斯·约阿希姆 Hans Joachim（1980）。诺伯特威纳。Biographien hervorragender Naturwissenschaftler，Techniker和Mediziner。

外部链接

编者推荐

如想再多了解维纳可点击

本中文词条由趣木木用户参与编译，欢迎在讨论页面留言

本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

↑ "A simplification in the logic of relations". Proc. Camb. Phil. Soc. 13: 387–390. 1912–14.
↑ van Heijenoort, Jean (1967). From Frege to Gödel: A Source Book in Mathematical Logic, 1879–1931. Harvard University Press. pp. 224–7.
↑ Wiener, Norbert (1930). "Generalized harmonic analysis". Acta Math. 55 (1): 117–258. doi:10.1007/BF02546511.

↑ The Fourier Integral and Certain of its Applications Cambridge Univ. Press; reprint by Dover, CUP Archive 1988

↑ Levinson, N. (1966). "Norbert Wiener 1894–1964". Bull. Amer. Math. Soc. 72 (1 Part 2): 1–33. doi:10.1090/S0002-9904-1966-11450-7.
↑ Invention: The Care and Feeding of Ideas. MIT Press. 1993. ISBN 978-0-262-73111-9. https://archive.org/details/inventioncarefee0000wien.
↑ Reardon, Joan. As Always, Julia. Houghton Mifflin, 2010. 223.
↑ Liu, Cixin (2015). The Three Body Problem. Chongqing Publishing Group. ISBN 9787229100605.
↑ Heinlein, Robert (1957). "14". Citizen of the Galaxy. Charles Scribner's Sons.
↑ "G.G. Tonet – Why?". Discogs. Retrieved 2 May 2019.

[1] "A simplification in the logic of relations". Proc. Camb. Phil. Soc. 13: 387–390. 1912–14.

[2] van Heijenoort, Jean (1967). From Frege to Gödel: A Source Book in Mathematical Logic, 1879–1931. Harvard University Press. pp. 224–7.

[3] Wiener, Norbert (1930). "Generalized harmonic analysis". Acta Math. 55 (1): 117–258. doi:10.1007/BF02546511.

[4] The Fourier Integral and Certain of its Applications Cambridge Univ. Press; reprint by Dover, CUP Archive 1988
v
t
e
Inline tags
Attribution

{{Attribution needed}}

{{By whom}}

{{Weasel-inline}}

{{Which?}}

{{Who}}

Citation

{{Better source}}

{{Citation needed}}
{{Citation needed span}}

{{Reference necessary}}

{{Citation needed (lead)}}

{{Failed verification}}

{{Full}}

{{Primary source-inline}}

{{Request quotation}}

{{Retracted}}

{{Third-party-inline}}

Incomplete

{{Author missing}}

{{Author incomplete}}

{{Date missing}}

{{ISBN missing}}

{{Page needed}}

{{Publisher missing}}

{{Title incomplete}}

{{Year missing}}

{{Dead link}}

Content

{{Contradict-inline}}

{{Contradiction-inline}}

{{Dubious|talk page section name}}

{{Examples}}

{{Inconsistent}}

{{List fact}}

{{Lopsided}}

{{POV-statement}}

Date and place

{{Clarify timeframe}}

{{Quantify}}

{{Update after}}

{{Update-small}}

{{When}}

{{Where}}

{{Year needed}}

Wikification

{{Disambiguation needed}}

{{Pronunciation needed}}

Wording

{{Ambiguous}}

{{Awkward}}

{{Buzz}}

{{Clarify}}

{{Clarify span}}

{{Definition}}

{{Elucidate}}

{{Expand acronym}}

{{Technical-statement}}

{{Vague|optional message to be displayed on mouseover}}

{{Why?}}

Category

[5] v

[6] t

[7] e

[8] {{Attribution needed}}

[9] {{By whom}}

[10] {{Weasel-inline}}

[11] {{Which?}}

[12] {{Who}}

[13] {{Better source}}

[14] {{Citation needed}}
{{Citation needed span}}

{{Reference necessary}}

[15] {{Citation needed span}}

[16] {{Reference necessary}}

[17] {{Citation needed (lead)}}

[18] {{Failed verification}}

[19] {{Full}}

[20] {{Primary source-inline}}

[21] {{Request quotation}}

[22] {{Retracted}}

[23] {{Third-party-inline}}

[24] {{Author missing}}

[25] {{Author incomplete}}

[26] {{Date missing}}

[27] {{ISBN missing}}

[28] {{Page needed}}

[29] {{Publisher missing}}

[30] {{Title incomplete}}

[31] {{Year missing}}

[32] {{Dead link}}

[33] {{Contradict-inline}}

[34] {{Contradiction-inline}}

[35] {{Dubious|talk page section name}}

[36] {{Examples}}

[37] {{Inconsistent}}

[38] {{List fact}}

[39] {{Lopsided}}

[40] {{POV-statement}}

[41] {{Clarify timeframe}}

[42] {{Quantify}}

[43] {{Update after}}

[44] {{Update-small}}

[45] {{When}}

[46] {{Where}}

[47] {{Year needed}}

[48] {{Disambiguation needed}}

[49] {{Pronunciation needed}}

[50] {{Ambiguous}}

[51] {{Awkward}}

[52] {{Buzz}}

[53] {{Clarify}}

[54] {{Clarify span}}

[55] {{Definition}}

[56] {{Elucidate}}

[57] {{Expand acronym}}

[58] {{Technical-statement}}

[59] {{Vague|optional message to be displayed on mouseover}}

[60] {{Why?}}

[5] Levinson, N. (1966). "Norbert Wiener 1894–1964". Bull. Amer. Math. Soc. 72 (1 Part 2): 1–33. doi:10.1090/S0002-9904-1966-11450-7.

[6] Invention: The Care and Feeding of Ideas. MIT Press. 1993. ISBN 978-0-262-73111-9. https://archive.org/details/inventioncarefee0000wien.

[7] Reardon, Joan. As Always, Julia. Houghton Mifflin, 2010. 223.

[8] Liu, Cixin (2015). The Three Body Problem. Chongqing Publishing Group. ISBN 9787229100605.

[9] Heinlein, Robert (1957). "14". Citizen of the Galaxy. Charles Scribner's Sons.

[10] "G.G. Tonet – Why?". Discogs. Retrieved 2 May 2019.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]