分岔理论
此词条暂由彩云小译翻译,未经人工整理和审校,带来阅读不便,请见谅。
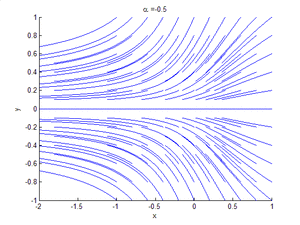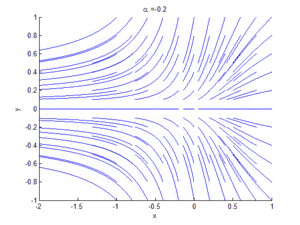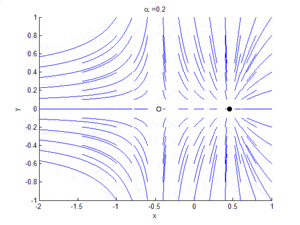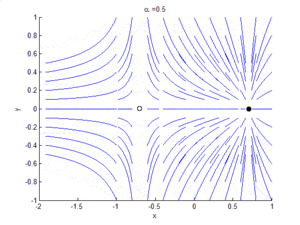
Phase portrait showing saddle-node bifurcation
显示鞍结分岔的相位图
Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations. Most commonly applied to the mathematical study of dynamical systems, a bifurcation occurs when a small smooth change made to the parameter values (the bifurcation parameters) of a system causes a sudden 'qualitative' or topological change in its behavior.[1] Bifurcations occur in both continuous systems (described by ODEs, DDEs or PDEs) and discrete systems (described by maps). The name "bifurcation" was first introduced by Henri Poincaré in 1885 in the first paper in mathematics showing such a behavior.[2] Henri Poincaré also later named various types of stationary points and classified them.
Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations. Most commonly applied to the mathematical study of dynamical systems, a bifurcation occurs when a small smooth change made to the parameter values (the bifurcation parameters) of a system causes a sudden 'qualitative' or topological change in its behavior. Bifurcations occur in both continuous systems (described by ODEs, DDEs or PDEs) and discrete systems (described by maps). The name "bifurcation" was first introduced by Henri Poincaré in 1885 in the first paper in mathematics showing such a behavior. Henri Poincaré also later named various types of stationary points and classified them.
分岔理论是数学中研究给定族的定性或拓扑结构的改变,例如向量场中的一族积分曲线以及微分方程的一族解。分岔常用于动力系统的数学研究中,是指当系统的参数值(分岔参数)发生微小平滑的变化时,系统发生突然的“定性”或拓扑变化。分岔在连续系统(由常微分方程、微分方程或偏微分方程描述)和离散系统(由映射描述)中均存在。1885年,亨利 · 庞加莱首次在论文中提到“分岔”一词,这也是数学中揭示该行为的第一篇论文,后来亨利 · 庞加莱也对不同的驻点进行了命名和分类。
Bifurcation types
It is useful to divide bifurcations into two principal classes:
It is useful to divide bifurcations into two principal classes:
将分支划分为两个主要类别是有用的:
- Local bifurcations, which can be analysed entirely through changes in the local stability properties of equilibria, periodic orbits or other invariant sets as parameters cross through critical thresholds; and
- Global bifurcations, which often occur when larger invariant sets of the system 'collide' with each other, or with equilibria of the system. They cannot be detected purely by a stability analysis of the equilibria (fixed points).
Local bifurcations
Period-halving bifurcations (L) leading to order, followed by period doubling bifurcations (R) leading to chaos.
周期分岔(l)导致有序,周期倍增分岔(r)导致混沌。
A local bifurcation occurs when a parameter change causes the stability of an equilibrium (or fixed point) to change. In continuous systems, this corresponds to the real part of an eigenvalue of an equilibrium passing through zero. In discrete systems (those described by maps rather than ODEs), this corresponds to a fixed point having a Floquet multiplier with modulus equal to one. In both cases, the equilibrium is non-hyperbolic at the bifurcation point.
A local bifurcation occurs when a parameter change causes the stability of an equilibrium (or fixed point) to change. In continuous systems, this corresponds to the real part of an eigenvalue of an equilibrium passing through zero. In discrete systems (those described by maps rather than ODEs), this corresponds to a fixed point having a Floquet multiplier with modulus equal to one. In both cases, the equilibrium is non-hyperbolic at the bifurcation point.
当参数变化引起平衡点(或不动点)的稳定性变化时,就会发生局部分岔。在连续系统中,这相当于一个平衡特征值通过零点的实部。在离散系统中(用映射而不是常微分方程描述的系统) ,这相当于一个具有模等于1的 Floquet 乘数的不动点。在这两种情况下,平衡点在分岔点都是非双曲的。
The topological changes in the phase portrait of the system can be confined to arbitrarily small neighbourhoods of the bifurcating fixed points by moving the bifurcation parameter close to the bifurcation point (hence 'local').
The topological changes in the phase portrait of the system can be confined to arbitrarily small neighbourhoods of the bifurcating fixed points by moving the bifurcation parameter close to the bifurcation point (hence 'local').
通过将分岔参数移动到分岔点附近,系统相图的拓扑变化可以局限于分岔不动点的任意小邻域内。
More technically, consider the continuous dynamical system described by the ODE
More technically, consider the continuous dynamical system described by the ODE
更严格地说,考虑常微分方程描述的连续动力系统
- [math]\displaystyle{ \dot x=f(x,\lambda)\quad f\colon\mathbb{R}^n\times\mathbb{R}\rightarrow\mathbb{R}^n. }[/math]
[math]\displaystyle{ \dot x=f(x,\lambda)\quad f\colon\mathbb{R}^n\times\mathbb{R}\rightarrow\mathbb{R}^n. }[/math]
数学点 x f (x,λ) f 冒号 mathbb { r } ^ n times mathbb { r } right tarrow mathbb { r } ^ n / math
A local bifurcation occurs at [math]\displaystyle{ (x_0,\lambda_0) }[/math] if the Jacobian matrix
A local bifurcation occurs at [math]\displaystyle{ (x_0,\lambda_0) }[/math] if the Jacobian matrix
如果雅可比矩阵的数学(x0, lambda 0) /
[math]\displaystyle{ \textrm{d}f_{x_0,\lambda_0} }[/math]
[math]\displaystyle{ \textrm{d}f_{x_0,\lambda_0} }[/math]
0,lambda 0} / math
has an eigenvalue with zero real part. If the eigenvalue is equal to zero, the bifurcation is a steady state bifurcation, but if the eigenvalue is non-zero but purely imaginary, this is a Hopf bifurcation.
has an eigenvalue with zero real part. If the eigenvalue is equal to zero, the bifurcation is a steady state bifurcation, but if the eigenvalue is non-zero but purely imaginary, this is a Hopf bifurcation.
有一个实部为零的特征值。如果特征值等于零,则分岔为稳态分岔,但如果特征值非零而纯为虚数,则为霍普夫分岔。
For discrete dynamical systems, consider the system
For discrete dynamical systems, consider the system
对于离散动力系统,考虑系统
- [math]\displaystyle{ x_{n+1}=f(x_n,\lambda)\,. }[/math]
[math]\displaystyle{ x_{n+1}=f(x_n,\lambda)\,. }[/math]
Math x { n + 1} f (xn, lambda) ,. / math
Then a local bifurcation occurs at [math]\displaystyle{ (x_0,\lambda_0) }[/math] if the matrix
Then a local bifurcation occurs at [math]\displaystyle{ (x_0,\lambda_0) }[/math] if the matrix
然后在 math (x0, lambda 0) / math if the matrix
[math]\displaystyle{ \textrm{d}f_{x_0,\lambda_0} }[/math]
[math]\displaystyle{ \textrm{d}f_{x_0,\lambda_0} }[/math]
0,lambda 0} / math
has an eigenvalue with modulus equal to one. If the eigenvalue is equal to one, the bifurcation is either a saddle-node (often called fold bifurcation in maps), transcritical or pitchfork bifurcation. If the eigenvalue is equal to −1, it is a period-doubling (or flip) bifurcation, and otherwise, it is a Hopf bifurcation.
has an eigenvalue with modulus equal to one. If the eigenvalue is equal to one, the bifurcation is either a saddle-node (often called fold bifurcation in maps), transcritical or pitchfork bifurcation. If the eigenvalue is equal to −1, it is a period-doubling (or flip) bifurcation, and otherwise, it is a Hopf bifurcation.
有一个模等于1的特征值。如果特征值等于1,则分岔可以是跨临界的鞍结点(在映射中通常称为折叠分岔) ,也可以是叉式分岔分岔。如果特征值等于-1,则为倍周期分叉,否则为霍普夫分岔分叉。
Examples of local bifurcations include:
Examples of local bifurcations include:
局部分岔的例子包括:
- Saddle-node (fold) bifurcation
- Period-doubling (flip) bifurcation
- Neimark–Sacker (secondary Hopf) bifurcation
Global bifurcations
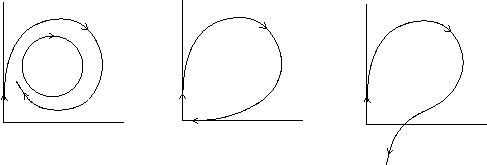
A phase portrait before, at, and after a homoclinic bifurcation in 2D. The periodic orbit grows until it collides with the saddle point. At the bifurcation point the period of the periodic orbit has grown to infinity and it has become a [[homoclinic orbit. After the bifurcation there is no longer a periodic orbit. Left panel: For small parameter values, there is a saddle point at the origin and a limit cycle in the first quadrant. Middle panel: As the bifurcation parameter increases, the limit cycle grows until it exactly intersects the saddle point, yielding an orbit of infinite duration. Right panel: When the bifurcation parameter increases further, the limit cycle disappears completely.]]
一个相位的肖像前,在,和之后的一个同宿分岔在2 d。周期轨道不断增长,直到与鞍点相撞。在分岔点,周期轨道的周期已经增长到无穷大,它已经成为一个[同宿轨道]。分岔后不再存在周期轨道。左面板: 对于小参数值,在原点有一个鞍点,在第一象限有一个极限环。中面板: 随着分岔参数的增加,极限环逐渐增大,直到与鞍点完全相交,形成一个无限长的轨道。右面板: 当分支参数进一步增加时,极限环完全消失
Global bifurcations occur when 'larger' invariant sets, such as periodic orbits, collide with equilibria. This causes changes in the topology of the trajectories in the phase space which cannot be confined to a small neighbourhood, as is the case with local bifurcations. In fact, the changes in topology extend out to an arbitrarily large distance (hence 'global').
Global bifurcations occur when 'larger' invariant sets, such as periodic orbits, collide with equilibria. This causes changes in the topology of the trajectories in the phase space which cannot be confined to a small neighbourhood, as is the case with local bifurcations. In fact, the changes in topology extend out to an arbitrarily large distance (hence 'global').
当“较大的”不变集(如周期轨道)与平衡碰撞时,就会出现全局分岔。这导致相空间中轨迹的拓扑结构发生变化,不能像局部分叉那样局限于一个小的邻域。事实上,拓扑的变化延伸到一个任意大的距离(因此是“全局”)。
Examples of global bifurcations include:
Examples of global bifurcations include:
全球分歧的例子包括:
- Homoclinic bifurcation in which a limit cycle collides with a saddle point.[3] Homoclinic bifurcations can occur supercritically or subcritically. The variant above is the "small" or "type I" homoclinic bifurcation. In 2D there is also the "big" or "type II" homoclinic bifurcation in which the homoclinic orbit "traps" the other ends of the unstable and stable manifolds of the saddle. In three or more dimensions, higher codimension bifurcations can occur, producing complicated, possibly chaotic dynamics.
- Heteroclinic bifurcation in which a limit cycle collides with two or more saddle points; they involve a heteroclinic cycle.[4] Heteroclinic bifurcations are of two types: resonance bifurcations and transverse bifurcations. Both types of bifurcation will result in the change of stability of the heteroclinic cycle. At a resonance bifurcation, the stability of the cycle changes when an algebraic condition on the eigenvalues of the equilibria in the cycle is satisfied. This is usually accompanied by the birth or death of a periodic orbit. A transverse bifurcation of a heteroclinic cycle is caused when the real part of a transverse eigenvalue of one of the equilibria in the cycle passes through zero. This will also cause a change in stability of the heteroclinic cycle.
- Infinite-period bifurcation in which a stable node and saddle point simultaneously occur on a limit cycle.[5] As the limit of a parameter approaches a certain critical value, the speed of the oscillation slows down and the period approaches infinity. The infinite-period bifurcation occurs at this critical value. Beyond the critical value, the two fixed points emerge continuously from each other on the limit cycle to disrupt the oscillation and form two saddle points.
- Blue sky catastrophe in which a limit cycle collides with a nonhyperbolic cycle.
Global bifurcations can also involve more complicated sets such as chaotic attractors (e.g. crises).
Global bifurcations can also involve more complicated sets such as chaotic attractors (e.g. crises).
全局分岔还可以涉及更复杂的集合,如混沌吸引子(例如混沌吸引子)。危机)。
Codimension of a bifurcation
The codimension of a bifurcation is the number of parameters which must be varied for the bifurcation to occur. This corresponds to the codimension of the parameter set for which the bifurcation occurs within the full space of parameters. Saddle-node bifurcations and Hopf bifurcations are the only generic local bifurcations which are really codimension-one (the others all having higher codimension). However, transcritical and pitchfork bifurcations are also often thought of as codimension-one, because the normal forms can be written with only one parameter.
The codimension of a bifurcation is the number of parameters which must be varied for the bifurcation to occur. This corresponds to the codimension of the parameter set for which the bifurcation occurs within the full space of parameters. Saddle-node bifurcations and Hopf bifurcations are the only generic local bifurcations which are really codimension-one (the others all having higher codimension). However, transcritical and pitchfork bifurcations are also often thought of as codimension-one, because the normal forms can be written with only one parameter.
分岔的余维是分岔发生时必须改变的参数个数。这对应于参数集的余维数,对于这个余维数,分岔发生在参数的整个空间。鞍结分支和 Hopf 分支是唯一真余维一的一般局部分支(其他分支均具有较高余维)。然而,跨临界分岔和干音叉分岔也经常被认为是余维数 -1,因为正规形可以只用一个参数来写。
An example of a well-studied codimension-two bifurcation is the Bogdanov–Takens bifurcation.
An example of a well-studied codimension-two bifurcation is the Bogdanov–Takens bifurcation.
Bogdanov-Takens 分岔是余维 -2分岔研究的一个很好的例子。
Applications in semiclassical and quantum physics
Bifurcation theory has been applied to connect quantum systems to the dynamics of their classical analogues in atomic systems,[6][7][8] molecular systems,[9] and resonant tunneling diodes.[10] Bifurcation theory has also been applied to the study of laser dynamics[11] and a number of theoretical examples which are difficult to access experimentally such as the kicked top[12] and coupled quantum wells.[13] The dominant reason for the link between quantum systems and bifurcations in the classical equations of motion is that at bifurcations, the signature of classical orbits becomes large, as Martin Gutzwiller points out in his classic[14] work on quantum chaos.[15] Many kinds of bifurcations have been studied with regard to links between classical and quantum dynamics including saddle node bifurcations, Hopf bifurcations, umbilic bifurcations, period doubling bifurcations, reconnection bifurcations, tangent bifurcations, and cusp bifurcations.
Bifurcation theory has been applied to connect quantum systems to the dynamics of their classical analogues in atomic systems, molecular systems, and resonant tunneling diodes. Bifurcation theory has also been applied to the study of laser dynamics and a number of theoretical examples which are difficult to access experimentally such as the kicked top and coupled quantum wells. The dominant reason for the link between quantum systems and bifurcations in the classical equations of motion is that at bifurcations, the signature of classical orbits becomes large, as Martin Gutzwiller points out in his classic work on quantum chaos. Many kinds of bifurcations have been studied with regard to links between classical and quantum dynamics including saddle node bifurcations, Hopf bifurcations, umbilic bifurcations, period doubling bifurcations, reconnection bifurcations, tangent bifurcations, and cusp bifurcations.
分岔理论已经应用于连接量子系统的动力学他们的经典类似物在原子系统,分子系统和共振隧穿二极管。分岔理论也被应用于激光动力学的研究,以及一些理论上难以通过实验获得的例子,如踢陀螺和耦合量子阱。正如 Martin Gutzwiller 在他关于量子混沌的经典著作中指出的那样,量子系统和经典运动方程之间存在联系的主要原因是在分岔时,经典轨道的特征变得很大。研究了经典动力学与量子动力学之间的联系,包括鞍点分岔、 Hopf 分岔、脐点分岔、周期倍增分岔、重联分岔、切线分岔和尖点分岔。
See also
Notes
- ↑ Blanchard, P.; Devaney, R. L.; Hall, G. R. (2006). Differential Equations. London: Thompson. pp. 96–111. ISBN 978-0-495-01265-8.
- ↑ Henri Poincaré. "L'Équilibre d'une masse fluide animée d'un mouvement de rotation". Acta Mathematica, vol.7, pp. 259-380, Sept 1885.
- ↑ Strogatz, Steven H. (1994). Nonlinear Dynamics and Chaos. Addison-Wesley. p. 262. ISBN 0-201-54344-3.
- ↑ Luo, Dingjun (1997). Bifurcation Theory and Methods of Dynamical Systems. World Scientific. p. 26. ISBN 981-02-2094-4.
- ↑ James P. Keener, "Infinite Period Bifurcation and Global Bifurcation Branches", SIAM Journal on Applied Mathematics, Vol. 41, No. 1 (August, 1981), pp. 127–144.
- ↑ Gao, J.; Delos, J. B. (1997). "Quantum manifestations of bifurcations of closed orbits in the photoabsorption spectra of atoms in electric fields". Phys. Rev. A. 56 (1): 356–364. Bibcode:1997PhRvA..56..356G. doi:10.1103/PhysRevA.56.356.
- ↑ Peters, A. D.; Jaffé, C.; Delos, J. B. (1994). "Quantum Manifestations of Bifurcations of Classical Orbits: An Exactly Solvable Model". Phys. Rev. Lett. 73 (21): 2825–2828. Bibcode:1994PhRvL..73.2825P. doi:10.1103/PhysRevLett.73.2825. PMID 10057205.
- ↑ Courtney, Michael; Jiao, Hong; Spellmeyer, Neal; Kleppner, Daniel; Gao, J.; Delos, J. B.; et al. (1995). "Closed Orbit Bifurcations in Continuum Stark Spectra". Phys. Rev. Lett. 74 (9): 1538–1541. Bibcode:1995PhRvL..74.1538C. doi:10.1103/PhysRevLett.74.1538. PMID 10059054.
- ↑ Founargiotakis, M.; Farantos, S. C.; Skokos, Ch.; Contopoulos, G. (1997). "Bifurcation diagrams of periodic orbits for unbound molecular systems: FH2". Chemical Physics Letters. 277 (5–6): 456–464. Bibcode:1997CPL...277..456F. doi:10.1016/S0009-2614(97)00931-7.
- ↑ Monteiro, T. S.; Saraga, D. S. (2001). "Quantum Wells in Tilted Fields:Semiclassical Amplitudes and Phase Coherence Times". Foundations of Physics. 31 (2): 355–370. doi:10.1023/A:1017546721313.
{{cite journal}}: Unknown parameter|lastauthoramp=ignored (help) - ↑ Wieczorek, S.; Krauskopf, B.; Simpson, T. B.; Lenstra, D. (2005). "The dynamical complexity of optically injected semiconductor lasers". Physics Reports. 416 (1–2): 1–128. Bibcode:2005PhR...416....1W. doi:10.1016/j.physrep.2005.06.003.
{{cite journal}}: Unknown parameter|lastauthoramp=ignored (help) - ↑ Stamatiou, G.; Ghikas, D. P. K. (2007). "Quantum entanglement dependence on bifurcations and scars in non-autonomous systems. The case of quantum kicked top". Physics Letters A. 368 (3–4): 206–214. arXiv:quant-ph/0702172. Bibcode:2007PhLA..368..206S. doi:10.1016/j.physleta.2007.04.003.
{{cite journal}}: Unknown parameter|lastauthoramp=ignored (help) - ↑ Galan, J.; Freire, E. (1999). "Chaos in a Mean Field Model of Coupled Quantum Wells; Bifurcations of Periodic Orbits in a Symmetric Hamiltonian System". Reports on Mathematical Physics. 44 (1–2): 87–94. Bibcode:1999RpMP...44...87G. doi:10.1016/S0034-4877(99)80148-7.
- ↑ Kleppner, D.; Delos, J. B. (2001). "Beyond quantum mechanics: Insights from the work of Martin Gutzwiller". Foundations of Physics. 31 (4): 593–612. doi:10.1023/A:1017512925106.
- ↑ Gutzwiller, Martin C. (1990). Chaos in Classical and Quantum Mechanics. New York: Springer-Verlag. ISBN 978-0-387-97173-5.
References
- Afrajmovich, V. S.表达式错误:无法识别的词语“etal”。 (1994). Bifurcation Theory and Catastrophe Theory. ISBN 978-3-540-65379-0.
- Wiggins, Stephen (1988). Global bifurcations and Chaos: Analytical Methods. New York: Springer. ISBN 978-0-387-96775-2. https://books.google.com/books?id=s1zdBwAAQBAJ.
External links
- Bifurcations and Two Dimensional Flows by Elmer G. Wiens
- Introduction to Bifurcation theory by John David Crawford
Category:Nonlinear systems
类别: 非线性系统
This page was moved from wikipedia:en:Bifurcation theory. Its edit history can be viewed at 分岔理论/edithistory