AP算法

简介

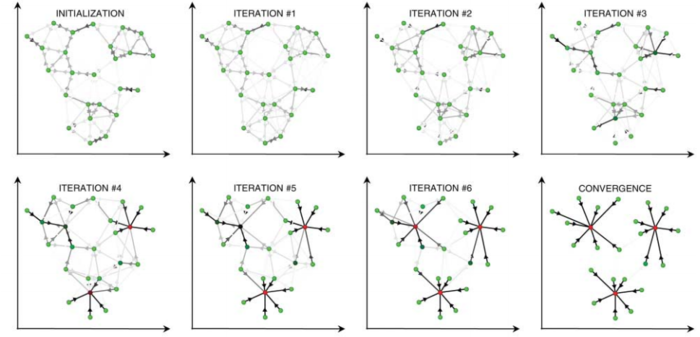
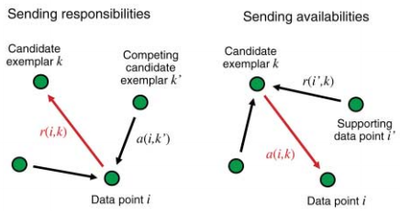
affinity propagation是Frey和Dueck在2007年发表在Science上的聚类算法。从更广义的角度说，它属于消息传递算法的一种。原始文献见这里，这里有关于AP算法的问答，包括适用的数据量大小和计算速度等细节。和k-means等它聚类算法一样，它的输入是一个N * N 的相似矩阵。在这个相似矩阵上，算法通过在数据点之间传递信息（责任和可用性，前者决定点i有多大意愿选择k作为自己的代表例子，后者决定k有多大意愿决定把i选择做代表），不断修改聚类中心的数量和位置，直到整个数据的净相似性（聚类中心k自己对自己的相似性+所有节点i!=k到k的相似性）达到最大。

Marc Mézard在同期Science对Frey和Dueck的文章给出了一个有趣的评论，他应用了卡拉瓦乔的一幅画，通过人物（数据点）之间的手势和眼神的交流来解释AP是如何工作，选出一群人的焦点的（见下图）。

优势

比起k-means方法，这种方法的好处是：

不需要事先指定聚类的数量

在affinity propagation中聚类的数量是由偏好的设定和数据的结构共同决定的。一般默认将所有的数据点的偏好设为相似矩阵的中位数。节点会比较自己的偏好和与其他节点之间的相似性，如果后者更高，就选择后者作为例子，反之则自己做例子。所以一开始如果把所有的偏好都设成0或大于0，而相似矩阵上的元素是负值（例如负的欧式距离），那么每个节点都会成为例子,也就是最后举出来N类。如果偏好被设成一个比较小的值，例如相似矩阵的中位数，那么就会在迭代过程中自发形成聚类的团块数量。

聚类的结果不会变化

kmeans方法是先随机抽样生成聚类中心或者例子，但AP则是在每一轮中同时考虑所有的节点，所以后者是一个确定性模型，也就意味着聚类的结果不会随机变化。

适用于非对称相似性矩阵，甚至不满足三角关系的相似性数据

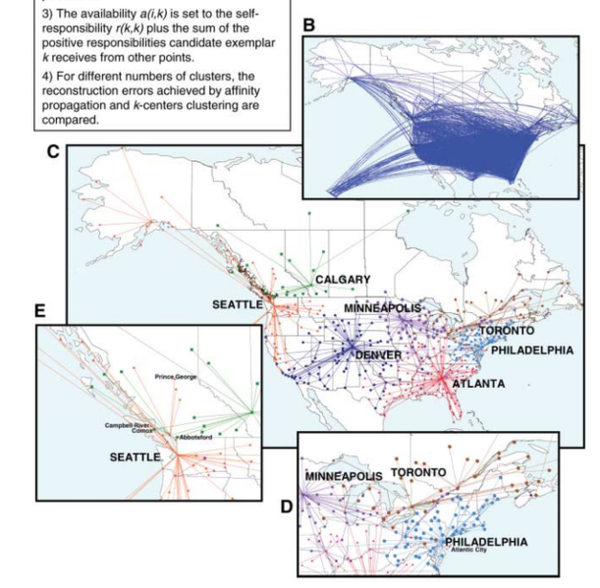
kmeans方法中，相似性矩阵是对称的，即[math]\displaystyle{ \s(i,j) }[/math]=:[math]\displaystyle{ \s(j,i) }[/math]，但是AP并没有这个要求。后者甚至适用于不满足三角关系的情况。在2007年的论文中，作者分析的美国和加拿大的航班网络（网络也可以看做是一个相似性矩阵，相似性权重为网络连边上的流量或者别的统计量，本案例中是一个城市到另一个城市的飞行时间）。在这个网络里，相似性是城市之间的飞行时间，这个变量是不满足三角关系的。例如A->B的平均飞行时间不一定就小于A->C+C->B的平均飞行时间（因为前者可能会没有直达飞机而要中途在别处转机，而且地球是一个球体）。在这个案例中，AP给出了很好的划分结果。

适用于稀疏的相似性矩阵

因为责任和可用性两种信息是在相似性矩阵的基础上计算和迭代，所以算法只利用了相似性信息。当矩阵中有大量元素为空的时候，AP仍然可以给出聚类，而且速度更快。

劣势

AP的劣势是充分识别了数据内部的结构后，对于许多真实数据，都会聚出比较多的类，因此在聚类数量在1-5时，速度没有K-means快，效果也不一定好。具体来说，AP算法复杂度为O(N*N*logN)，而K-Means是O(N*K)。因此当N比较大时(N>3000)，AP聚类算法往往需要算很久。

应用

因为AP只是一种聚类算法，所以在机器学习里是非特定领域的，文章中给出了四个例子，对生物基因的聚类，对人脸的聚类，对文章主题句的提取（这个比较有意思，作者把自己发表的这篇文章提出四句话），和对城市之间航运网络的聚类。

在python的sklearn包里带了AP算法，应用起来也是很方便的：

首先调用包

    from sklearn.cluster import AffinityPropagation
    from sklearn import metrics
    from sklearn.datasets.samples_generator import make_blobs
    import pylab as pl
    from itertools import cycle

其次生成模拟数据

   
    # Generate sample data
    centers = [[1, 1], [-1, -1], [1, -1]]
    X, labels_true = make_blobs(n_samples=300, centers=centers, cluster_std=0.5,
                                random_state=0)

接着拟合AP

    
    # Compute Affinity Propagation
    af = AffinityPropagation(preference=-50).fit(X)
    cluster_centers_indices = af.cluster_centers_indices_
    labels = af.labels_
    n_clusters_ = len(cluster_centers_indices)
    
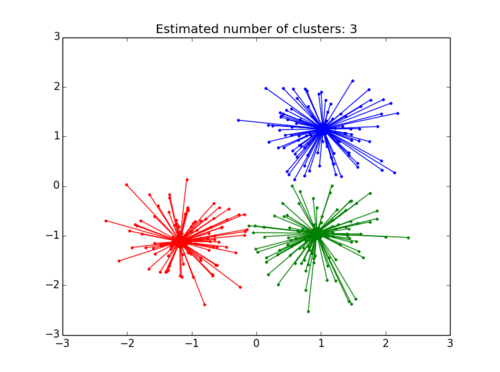
    print('Estimated number of clusters: %d' % n_clusters_)
    print("Homogeneity: %0.3f" % metrics.homogeneity_score(labels_true, labels))
    print("Completeness: %0.3f" % metrics.completeness_score(labels_true, labels))
    print("V-measure: %0.3f" % metrics.v_measure_score(labels_true, labels))
    print("Adjusted Rand Index: %0.3f"
          % metrics.adjusted_rand_score(labels_true, labels))
    print("Adjusted Mutual Information: %0.3f"
          % metrics.adjusted_mutual_info_score(labels_true, labels))
    print("Silhouette Coefficient: %0.3f"
          % metrics.silhouette_score(X, labels, metric='sqeuclidean'))

最后绘制出结果

    
    # Plot result
    pl.close('all')
    pl.figure(1)
    pl.clf()
    colors = cycle('bgrcmykbgrcmykbgrcmykbgrcmyk')
    pl.title('Estimated number of clusters: %d' % n_clusters_)
    for k, col in zip(range(n_clusters_), colors):
        class_members = labels == k
        cluster_center = X[cluster_centers_indices[k]]
        pl.plot(X[class_members, 0], X[class_members, 1], col + '.')
        pl.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col,
                markeredgecolor='k', markersize=14)
        for x in X[class_members]:
            pl.plot([cluster_center[0], x[0]], [cluster_center[1], x[1]], col)

每次运行的结果都是一样的。