熵
熵 Entropy,是一种测量在动力学方面不能做功的能量总数,也就是当总体的熵增加,其做功能力也下降,熵的量度正是能量退化的指标。熵亦被用于计算一个系统中的失序现象,也就是计算该系统混乱的程度。熵是一个描述系统状态的函数,但是经常用熵的参考值和变化量进行分析比较,它在控制论、概率论、数论、天体物理、生命科学等领域都有重要应用,在不同的学科中也有引申出的更为具体的定义,是各领域十分重要的参量。
熵的热力学定义
在统计力学中,熵是热力学系统的广延量。它与组成系统宏观量(如体积、压力和温度)的微观状态(也叫微观态)的数量紧密相关。熵表示定义宏观量的不同状态的数量Ω。[1]假设每个微观态存在的概率相等,熵S则定义为微观状态数的自然对数乘以玻尔兹曼常数kB. 即 [math]\displaystyle{ S=k_B\ln(\Omega) }[/math]。
一般情况,微观系统的微观状态数目非常大。例如,理想气体的熵与气体分子数量N成正比。标准条件(常温常压)下,22.4升的气体中的分子数大约为6.022 × 1023(阿伏伽德罗常数)。
热力学第二定律告诉我们孤立系统的熵不随时间减少。孤立系统自发地向熵最大热平衡演化。非孤立系统,比如有机体,熵会减少,使得它们的环境熵增或者不变。因此,宇宙的总熵一直增加。熵是系统状态的函数,所以熵变由系统的初始状态和结束状态决定。理想的可逆过程中,熵不变;不可逆过程熵增加。
由于熵由随机微观态数目决定,假如系统的宏观状态确定,熵与将系统状态描述精确所需要的其他信息相关。因此,熵也常常被用来描述系统的无序性或随机性,或者用来表达相关信息缺乏程度。[2]熵的概念在信息论中非常重要。
历史
法国数学家拉扎尔·卡诺(Lazare Carnot)在1803年发表的《Fundamental Principles of Equilibrium and Movement》一文提出,在任何机器中,运动部分的加速和碰撞代表着动能的损失;任何自然过程都内在地倾向于耗散有用的能量。在这份工作的基础上,1824年他的儿子萨迪·卡诺 (Sandi Carnot)发表《Reflection on the Motive Power of Fire》,文中提出,所有的热机,热量从高温体到低温体的热传递可以做功或者转化为动能。他用水如何从水车落下做类比。这是热力学第二定律的早期理解。[3]Carnot对热能的观点部分建立在18世纪早期‘牛顿的假说’:热和光都是不能被销毁的物质形式,只能被其他物质相互吸引或排斥;另一部分建立在当时本杰明·汤普森(Benjamin Thompson)提出的摩擦可以产生热,比如炮弹的原理。[4]Carnot认为,如果工作物质,比如蒸汽,完成一个完整的机械循环后会回到初始状态,那么“工作体没有发生变化”。
1842年,詹姆斯·焦耳(James Joule)从热摩擦实验中总结的热力学第一定律解释了能量的概念以及在所有过程中的能量转化。但是第一定律无法量化解释摩擦和耗散效应。
1850年至1860年间,德国物理学家鲁道夫·克劳修斯(Rudolf Clausius)反对(热机的)工作体没有发生变化的推测,并通过质疑做功完成时有用热的内在损失,比如摩擦生热,给出了此“变化”的数学解释。Clausius把热力学系统的熵(比如耗散的能量)或化学物质状态改变时的工作体描述为物质转化物质。[5]这与艾萨克·牛顿(Isaac Newton)的热是有质量的不可摧毁的粒子的理论相反。
随后,路德维希·玻尔兹曼(Ludwig Boltzmann)、约西亚·威拉德·吉布斯(Josiah Willard Gibbs)和詹姆斯·克莱克·麦克斯韦(James Clerk Maxwell)等科学家建立熵的统计学基础。1877年,Boltzman将测量理想气体粒子系统的熵可视化,这个框架下熵与理想气体所占微观态数目的自然对数成正比。至此,统计热力学中关键的问题是给定能量E,确定N个全同系统的分布状态。Carathéodory通过路径和可积性把熵与过程不可逆的数学定义联系起来
词语来源
1865年,Clausius用希腊语‘转化’ transformation一词给熵 (Entropy,Entropie)命名,意为“一个与系统表象有关的状态微分”。[6]他认为“transformational content”( (Verwandlungsinhalt) )是熵的近义词,与“thermal and ergonal content”(Wärme- und Werkinhalt)中的U同义。他倾向于用熵 Entropy一词作为能量的近义词,因为他发现这两个词的概念近乎“物理意义相似”。这个词是由ἔργον ('work') 的词根τροπή('transformation')替换而来。[7]
定义和表述
熵有两种等价定义:热力学定义和统计力学定义。历史上,经典热力学定义先被提出。此观点认为,不考虑系统的微观细节,而是用经验上定义的热力学变量,如温度、气压、熵和热容来描述。经典热力学假设存在平衡态,但是更多的是尝试定义非平衡系统的熵。
统计物理学对熵以及其他热力学性质的定义发展于经典定义之后。此观点认为,热力学性质是被系统的微观构成的运动的统计定义的。这个定义先是模拟在由牛顿粒子组成的气体中提出,随后发现在量子粒子中也成立(光子、声子、自旋等)
状态函数
许多热力学量都是状态函数,意味着特定的热力学状态(不同于系统的微观状态)有特定的值。通常情况下,如果已知系统的两个热力学性质,那么可以确定此系统的状态,系统的另外一个热力学性质也可以被确定。比如,一定温度和压力下的一些气体的状态被这些量所确定,所以其体积也是确定的。再比如,一定温度和气压下的只存在单相的系统,不仅可以确定其体积,还可以确定它的熵。[9]熵是状态函数因为它有用。在卡诺循环中,工作流体回到初始工作时的状态,所以状态函数(如: 熵 Entropy)在一个可逆循环中的线积分是零。
可逆过程
可逆过程中的熵不变。可逆过程是指能做最大功的同时保持热动平衡态。任何快速偏离热动平衡的过程都不可逆。在这些过程中,能量损失变为热量,总熵增加,最大输出功也不能达到。更具体的,可逆过程中熵守恒,而不可逆过程熵不守恒。[10]比如卡诺循环,热量从热库经过冷库代表着熵增,输出功代表着可以被用于让热机回到上一个状态的熵减。因此如果过程是可逆的,系统的总熵为零。不可逆过程熵增加。[11]
卡诺循环
熵的概念来自Rudolf Clausius对卡诺循环的研究。[12] 在卡诺循环中,热量[math]\displaystyle{ Q_\text{H} }[/math]在温度[math]\displaystyle{ T_H }[/math]下从“热”储库中被等温吸收,并作为热量[math]\displaystyle{ Q_C }[/math]被等温地释放到[math]\displaystyle{ T_C }[/math]处的“冷”库中。 根据卡诺原理 (Carnot Theory),只有在存在温差的情况下,系统才能产生功,并且功应该是温差和吸收热量[math]\displaystyle{ Q_\text{H} }[/math]的某种函数。 卡诺没有区分[math]\displaystyle{ Q_\text{H} }[/math]和[math]\displaystyle{ Q_C }[/math],因为他使用了一个错误的假设,即热量理论是有效的,因此,当[math]\displaystyle{ Q_\text{H} }[/math]大于[math]\displaystyle{ Q_C }[/math]时,热量就得以保存(错误的假设,[math]\displaystyle{ Q_\text{H} }[/math]和[math]\displaystyle{ Q_C }[/math]相等)[13] [14] 通过Clausius和威廉·汤姆森(开尔文男爵,Kelvin)的努力,现在知道,热机可以产生的最大功是卡诺效率和从热库吸收的热量的乘积:
[math]\displaystyle{ W=(\frac{T_\text{H}-T_\text{C}}{T_\text{H}})Q_\text{H} = (1-\frac{T_\text{C}}{T_\text{H}}) Q_\text{H} }[/math] (1)
为了得到卡诺效率,即[math]\displaystyle{ 1-\frac{T_\text{C}}{T_\text{H}} }[/math],Kelvin必须借助卡诺-克拉珀龙方程来评估等温膨胀过程中功输出与吸收的热量之比,其中包含一个名为卡诺函数的未知函数。Joule在给Kelvin的信中提出了卡诺函数可能是从零温度开始测量的温度的可能性。 这使Kelvin得以建立自己的绝对温度标度。[15] 众所周知,系统产生的功是从热库吸收的热量与释放到冷库的热量之差:
[math]\displaystyle{ W=Q_\text{H}-Q_\text{C} }[/math] (2)
由于后者在整个循环内都是有效的,这给了克劳修斯一个指示,即在循环的每个阶段,功和热将不相等,但是它们的差将是状态函数,该函数将在循环完成时消失。 状态函数被称为内部能量,它称为热力学的第一定律。[16]
现在,使等式(1)等于等式(2)得到:
[math]\displaystyle{ \frac{Q_\text{H}}{T_\text{H}}-\frac{Q_\text{C}}{T_\text{C}}=0 }[/math]
或者
[math]\displaystyle{ \frac{Q_\text{H}}{T_\text{H}}=\frac{Q_\text{C}}{T_\text{C}} }[/math]。
这意味着在卡诺循环的整个循环中都有一个守恒的状态函数。 克劳修斯称这种状态函数为熵。 可以看到,熵是通过数学而不是通过实验室结果发现的。 它是一种数学构造,没有简单的物理类比。 这使该概念有些模糊或抽象,类似于能量的概念如何产生。
然后,Clausius提出,如果系统产生的功少于卡诺原理预测的功,会发生什么情况。 第一个方程的右侧将是系统输出的功的上限,现在将其转换为不等式
[math]\displaystyle{ W\lt \left(1-\frac{T_\text{C}}{T_\text{H}}\right)Q_\text{H} }[/math]
当使用第二个方程将功表示为热量差时,我们得到
[math]\displaystyle{ Q_\text{H}-Q_\text{C}\lt \left(1-\frac{T_\text{C}}{T_\text{H}}\right)Q_\text{H} }[/math]
或者
[math]\displaystyle{ Q_\text{C}\gt \frac{T_\text{C}}{T_\text{H}}Q_\text{H} }[/math]
因此,比卡诺循环中更多的热量提供给冷库。 如果我们用两种状态的Si = Qi / Ti表示熵,则上述不等式可以写成熵减小的形式
[math]\displaystyle{ S_\text{H}-S_\text{C}\lt 0 }[/math] 或者 [math]\displaystyle{ S_\text{H}\lt S_\text{C} }[/math]
离开系统的熵大于进入系统的熵,这意味着某些不可逆的过程会阻止循环产生卡诺方程所预测的最大功。
卡诺循环和效率之所以有用,是因为它们定义了可能的功输出的上限以及任何经典热力学系统的效率。 可以从卡诺循环的角度分析其他循环,例如奥托循环(Otto Cycle), 迪塞尔循环(Diesel Cycle)和布雷顿循环(Brayton Cycle)。 任何将热量转换为功并且声称产生的效率高于卡诺效率的机器或过程都是不可发生的,因为它违反了热力学第二定律。 对于系统中极少数的粒子,必须使用统计热力学。 诸如光伏电池之类的设备的效率需要从量子力学的角度进行分析。
经典热力学
熵的热力学定义是Rudolf Clausius在1850年代初期提出的,它本质上描述了如何在孤立系统的热力学平衡及其部分中测量熵。 Clausius创造了“熵”一词,将其作为一个广延的热力学变量,证明其对卡诺循环很有用。 卡诺循环中等温过程的热传递与系统温度(称为系统绝对温度)成正比。 这种关系用熵的增量表示,该熵的增量等于传热增量除以温度,这在热力学循环中会发生变化,但最终在每个循环结束时相同。 因此熵被发现是状态函数,特别是系统的热力学状态。
Clausius的定义基于可逆过程,但也有不可逆过程改变熵。 根据热力学第二定律,对于不可逆过程,孤立系统的熵总是增加。 孤立系统和封闭系统之间的区别在于,热量可能不会流入孤立系统或从孤立系统中流出,但是热量可能会流入封闭系统或从封闭系统中流出。 然而,对于封闭系统和隔离系统,甚至在开放系统中,都可能发生不可逆的热力学过程。
根据克劳修斯不等式,对于一个可逆过程[math]\displaystyle{ \oint \frac{\delta Q_\text{rev}}{T} = 0 }[/math]。这意味着线积分[math]\displaystyle{ \int_\text{L} \frac{\delta Q_\text{rev}}{T} }[/math]与路径无关。所以我们可以定义一个叫熵的状态函数S,满足[math]\displaystyle{ d S = \frac{\delta Q_\text{rev}}{T} }[/math]。
为了找到系统中任何两个状态之间的熵差,必须通过对初始状态和最终状态之间的某些可逆路径进行积分。[17] 由于熵是状态函数,因此对于不可逆路径,系统的熵变化与在相同两个状态之间的可逆路径的熵变化相同。[18] 但是,周围环境的熵变化是不同的。
我们只能通过整合以上公式来获得熵的变化。为了获得熵的绝对值,我们需要热力学第三定律,该定律规定对于完美的晶体,S = 0(绝对零度时)。
从宏观的角度来看,在经典热力学中,熵被解释为热力学系统的状态函数:即,仅取决于系统当前状态的属性,而与该状态如何实现无关。 在任何系统释放能量ΔE且其熵下降ΔS的过程中,必须以不可用的热量将至少至少该能量的[math]\displaystyle{ T_\text{R} }[/math]ΔS释放给系统周围环境([math]\displaystyle{ T_\text{R} }[/math]是系统外部环境的温度)。 否则,该过程将无法进行。 在经典热力学中,仅当系统处于热力学平衡状态时才定义其熵。
统计物理
统计定义是路德维希·博尔兹曼(Ludwig Boltzmann)在1870年代通过分析系统微观组分的统计行为得出的。Boltzmann证明,这种熵的定义等价于热力学熵,比例常数被称为玻耳兹曼常数。 总而言之,熵的热力学定义提供了熵的实验定义,而熵的统计定义扩展了该概念,提供了对其性质的解释和更深刻的理解。
用吉布斯(Gibbs)的语言,统计力学中对熵的解释是用来衡量不确定性或混合状态,在考虑了系统的可观察到的宏观特性(例如温度,压力和体积)后,该信息仍然存在。对于给定的一组宏观变量,熵衡量了系统在不同可能的微状态上概率分布的程度。与表征可观察到的平均量的宏观状态相反,微观状态指定了有关系统的所有分子细节,包括每个分子的位置和速度。系统以可观的概率获得的此类状态越多,熵越大。在统计力学中,熵是对系统排列方式数量的一种度量,通常被视为“无序”的度量(熵越高,无序性越高)。[19] [20] [21]该定义将熵描述为与可能导致系统观察到的宏观状态的单个原子和系统分子(微观状态)的可能微观构型数目的自然对数成比例。比例常数是玻耳兹曼常数。
玻耳兹曼常数和熵的维度是能量除以温度,在国际单位制中,单位为焦耳每开尔文焦耳(J⋅K-1)(或kg·m2⋅s−2⋅K−1 基本单位)。 物质的熵通常以强度形式给出-单位质量的熵(SI单位:J⋅K-1⋅kg-1)或单位物质的量的熵(SI单位:J⋅K-1⋅mol -1)。
具体来说,熵是对被占用概率很高的状态数的对数度量:
[math]\displaystyle{ S = -k_{\text{B}}\sum_i p_i \log p_i, }[/math]
或者等价来说,微观态被占据的几率的自然对数的期望值:
[math]\displaystyle{ S = -k_{\text{B}} E_{\text{i}}(\log p_i) }[/math]
其中[math]\displaystyle{ k_\text{B} }[/math]是玻尔兹曼常数,等于1.38065*10-23J/K
求和是指对系统所有可能的微观态求和,pi是系统在第i个微观态的可能性。该定义假设已选择了状态的基,因此没有关于其相对阶段的信息。 在不同的基中,更一般的表达式是:
[math]\displaystyle{ S = -k_{B} \operatorname{Tr}(\widehat{\rho} \log(\widehat{\rho})) }[/math]
其中,[math]\displaystyle{ \widehat{\rho} }[/math]是密度矩阵,Tr是迹线,log是矩阵对数。这种密度矩阵公式不需要在热平衡的情况下才成立,只要选择基态为能量本征态即可。 对于大多数实际目的,这可以作为熵的基本定义,因为S的所有其他公式都可以从中数学推导出,反之则不能。
在所谓的统计热力学的基本假设或统计力学的基本假设中,假定任何微状态的占据都是等可能的(即pi = 1 /Ω,其中Ω是微状态数); 这个假设通常对于平衡的孤立系统是合理的。[23]所以,上一个公式简化为:
[math]\displaystyle{ S = k_{B} \log \Omega. }[/math]
在热力学中,这种系统是体积固定,分子数和内部能量守恒的系统(微正则系统)。
熵的最一般的解释是度量我们对系统的不确定性。 系统的平衡状态使熵最大化,因为除了守恒变量之外,我们已经失去了所有有关初始条件的信息。 最大化熵会使我们对系统细节的无知最大化。[24] 这种不确定性不是日常主观的,而是实验方法和解释模型固有的不确定性。
解释模型在确定熵方面具有核心作用。 上面的“对于给定的一组宏观变量”的限定词具有深远的含义:如果两个观察者使用不同的宏观变量,他们将看到不同的熵。 例如,如果观察者A使用变量U,V和W,观察者B使用U,V,W,X,B通过更改X,可能会导致观察者A看到像违反热力学第二定律的现象。 换句话说,观察者所选择的一组宏观变量必须包括实验中可能变化的所有事物,否则,熵可能会降低![25]
可以为任何具有可逆动力学和满足细致平衡条件的马尔可夫过程定义熵。
Boltzmann的1896年《Lectures on Gas Theory》讲座中,他证明了该表达式给出了气相中原子和分子系统的熵的量度,从而为经典热力学的熵提供了量度。
系统熵
熵直接来自卡诺循环。 也可以描述为可逆热量除以温度。 熵是基本的状态函数。在热力学系统中,压力,密度和温度会随时间趋于常数,因为平衡状态比其他任何状态都具有更高的概率(更多的可能的微观状态组合)。
例如,室温空气中的一杯冰水,温暖的房间(环境)与冷的冰和水杯子(系统而非房间的一部分)之间的温度差开始趋于零,因为温暖环境的部分热能散布到冰和水的较冷系统中。 随着时间的流逝,玻璃及其内容物的温度与房间的温度将相等。 换句话说,随着部分能量分散到冰和水上,房间的熵降低了。
但是,如示例中所计算的,冰和水系统的熵增加的幅度大于周围房间的熵减小的幅度。 在一个孤立的系统中,例如将房间和冰水合在一起,能量从较热的位置散布到较冷的位置总是导致熵的净增加。 因此,当房间和冰水系统的“宇宙”达到温度平衡时,熵相对于初始状态变化最大。 热力学系统的熵是衡量反应平衡程度的一种量度。
热力学熵是一种非保守状态函数,在物理学和化学科学中具有重要意义。[19] [26] 历史上,熵的概念演变为解释为什么某些过程(受守恒定律限制)自发发生而时间逆转不能发生(也受守恒定律限制)的原因。 系统倾向于朝着熵增加的方向演化。[27] [28] 对于孤立的系统,熵永远不会降低。[26] 这一事实在科学中产生了几个重要的后果:首先,它限制“永动机”。 其次,它意味着熵的箭头与时间之箭具有相同的方向。 熵的增加对应于系统中不可逆的变化,因为一些能量被消耗为废热,从而限制了系统可以完成的工作量。[19] [20] [29] [30]
与许多其他状态函数不同,熵不能直接观察到,而必须进行计算。物质的熵可以用绝对零度下的标准摩尔熵(也称为绝对熵)计算,也可以与定义为零熵的其他参考状态的熵差计算。熵的大小是能量除以温度,在国际单位制中,熵的单位是焦耳每开尔文(J / K)。尽管这些单位与热容量相同,但两个概念却截然不同。[31]熵不是守恒的量:例如,在温度不均匀的孤立系统中,热量可能会不可逆地流动,并且温度会变得更加均匀,从而使熵增加。热力学第二定律指出,封闭系统的熵可能会增加或保持恒定。化学反应会引起熵的变化,并且熵在确定化学反应自发向哪个方向发挥着重要作用。
熵的一种字典定义是,它是“无法用于有用功的单位温度热能的量度”。 例如,处于均匀温度下的物质处于最大熵并且不能驱动热机。 温度不均匀的物质具有较低的熵(与允许均匀分布的热量相比),并且一些热能可以驱动热机。
当两种或多种不同的物质混合时,会出现熵增加的一种特殊情况,即混合熵。 如果物质处于相同的温度和压力下,则没有热交换或功的净交换–熵的变化完全是由于不同物质的混合。 在统计力学的水平上,这是由于混合时每个粒子的可用体积发生了变化。[32]
等价定义
统计力学中熵定义(吉布斯公式[math]\displaystyle{ S = -k_{B}\sum_i p_i \log p_i }[/math])与经典热力学([math]\displaystyle{ d S = \frac{\delta Q_\text{rev}}{T} }[/math]和热力学基本关系)之间的等价证明微正则系统、正则系统、巨正则系统和等温等压系统而著名。这些证明是基于广义玻尔兹曼分布的微观态的概率密度以及热力学内部能量作为系综平均 [math]\displaystyle{ U=\left\langle E_{i}\right\rangle }[/math][33]。然后使用热力学关系来得出众所周知的吉布斯熵公式。 然而,吉布斯熵公式和熵的热力学定义之间的等价关系不是基本的热力学关系,而是广义玻耳兹曼分布形式的结果。[34]
热力学第二定律
热力学第二定律要求,一般而言,任何系统的总熵都不能降低,除非其他系统的熵增加。因此,在与环境隔离的系统中,该系统的熵倾向于不降低。随之而来的是,如果不对冷物做功(施加),热量就不会从冷物流向热物。其次,任何一个循环运行的设备都不可能从单温度源中产生净功。净功的生产需要热量从较热源流向较冷源,或进行进行膨胀绝热冷却,产生绝热功。这样一来,不可能存在永动机系统。同理,在特定过程(例如化学反应)中,熵增加的减少意味着从能量角度来说,过程更有效。
根据热力学第二定律,不孤立系统的熵可能减小。例如,空调,可以冷却室内的空气,从而降低该系统中空气的熵。从房间(系统)散发出来的热量(空调将其散发并排放到外部空气中)对环境的熵的贡献始终大于该系统的空气熵的减小。因此,房间的熵加环境的熵的总和增加,遵循热力学第二定律。
在力学中,热力学第二定律与基本热力学关系相结合,限制了系统做有用工作的能力。[35]在温度T下,系统的熵变 以δq / T给出,该熵可逆地吸收了无限少量的热量δq。更明确地讲,能量T R 是无法做有用功等,其中T R是系统外部可接触到最冷的库或散热器的温度。有关更多讨论,请参见㶲 Exergy。
统计力学表明,熵由概率决定,因此即使在孤立的系统中混乱程度也可能减少。尽管这是可能的,但此类事件发生的可能性很小,因此(实际上)不可能发上。[36]
热力学第二定律的适用性限于接近或处于平衡状态的系统。[37]同时,支配远非均衡体系的定律仍有待商榷。适用于这种系统原理之一是最大熵产生原理。[38] [39]它要求非平衡系统往熵产生最大化发展。[40] [41]
应用
基本热动力学关系
一个系统的熵取决于它的内能和它的宏观变量,例如它的体积。在热力学极限中,这一事实导致方程式将内能U的变化与熵以及宏观变量的变化联系起来。这种关系称为基本热力学关系。如果外部压力p作为唯一的宏观变量施加在体积V上,则此关系为: [math]\displaystyle{ dU = T \, dS - p \, dV }[/math]
由于内能和熵都是温度T的单调函数,这意味着当一个能量指定熵和体积时,内能是固定的,即使从一个热平衡状态到另一个无限大的熵状态,该关系也有效。体积以非准静态的方式发生(因此,在此更改期间,系统可能与热平衡相差很远,因此可能不存在熵,压力和温度)。 基本的热力学关系意味着许多有效的热力学身份在总体上是有效的,与系统的微观细节无关。重要的例子是麦克斯韦关系和热容量之间的关系。
化学热力学中的熵
热力学熵在化学热力学中占有重要地位,因为熵可将变化量化并预测反应结果。热力学第二定律中,孤立系统的熵-包括研究的子系统以及其环境-在所有自发的化学和物理过程中增加。克劳修斯方程:δq(rev) / T =Δ S介绍熵变化的测量方式,Δ S。熵变化描述了化学反应的方向并量化了简单变化的程度,例如系统之间的传热–总是自发地从较热到较冷。 因此,在国际单位制(SI)中,热力学熵具有能量除以温度的维数和每开尔文的单位焦耳(J / K)。
热力学熵是一种广延的性质,这意味着它会随着系统的变大变小而变化。在许多过程中,将熵指定为与大小无关的强度属性是有用的,可以被作为研究的系统熵特征。比熵可以表示称相对于质量单位,通常是千克(单位:J⋅kg - 1⋅K -1)。此外,在化学中,它也被称为一摩尔物质,在这种情况下,它被称为摩尔熵,其单位为J⋅mol - 1⋅K -1。
因此,当约 0 K的一摩尔物质被周围的环境加热到298 K,q (rev) / T的增量的总和构成每个元素或化合物的标准摩尔熵,该物质表示298K的物质存储的能量。[42] [43]熵变也可用来测量物质的混合为最终混合物中相对量的总和。[44]
熵对于预测复杂化学反应的程度和方向同样至关重要。对于此类应用,ΔS 必须包含在系统及其周围环境的表达式中,其中ΔS(宇宙)= ΔS(环境)+ ΔS(系统)。经由一些步骤,该表达式变为,系统中的反应物和产物的吉布斯自由能等式:Δ G [系统的吉布斯自由能的变化] =Δ H [焓变化] - T Δ S [熵变] 。[42]
开放系统熵平衡关系
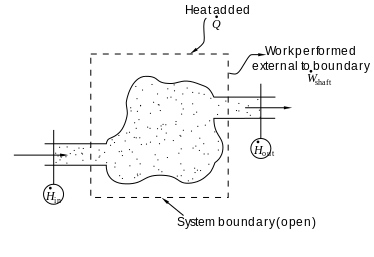
在化学工程中,热力学原理通常应用于“开放系统”,比如热量,功和质量流过系统边界的系统。两种热流[math]\displaystyle{ \dot{Q} }[/math]和功,和即[math]\displaystyle{ \dot{W} }[/math](轴功)和P(dV / dt)(压力-体积功)跨越系统边界,通常会引起系统熵的变化。由于热量的传递引起熵传递图片[math]\displaystyle{ \dot{Q} /{T} }[/math]其中T是系统在热流点的绝对热力学温度。如果有质量流越过系统边界,它们也会影响系统的总熵。就热量和功而言,该说明仅在以下情况下有效:当功和热量的传输的路径物理熵与物质进入和离开系统的路径不同时。[45] [46]
导出广义的熵平衡方程,我们从热力学系统中任何广延量 Θ 的变化都通用平衡方程开始,该量可以守恒,例如能量,或不守恒,例如熵。基本的通用平衡表达式表示dΘ/ dt,即系统中Θ的变化率,等于Θ在边界处进入系统的速率,减去Θ离开系统边界的速率,再加上系统内部产生Θ的速率。对于一个开放的热力学系统,其中热量和功是通过与物质传递路径分开的路径传递的,使用此一般平衡方程,广义熵S关于时间t的变化率的熵平衡方程为:[47] [注1]
[math]\displaystyle{ \frac{dS}{dt} =\sum\limits_{k=1}^K \dot{M}_k \hat{S}_k + \frac{\dot{Q}}{T} + \dot{S}_\text{gen} }[/math]
其中,
[math]\displaystyle{ \sum_{k=1}^K \dot{M}_k \hat{S}_k = {} }[/math]物质流入和流出系统(其中[math]\displaystyle{ \hat{S} }[/math]为单位质量的熵)。
[math]\displaystyle{ \frac{\dot{Q}}{T} = {} }[/math]由于热量跨系统边界流动而产生的熵流速率。
[math]\displaystyle{ \dot{S}_\text{gen} = {} }[/math] 系统内的熵产生率。熵的产生来自系统内的过程,包括化学反应,内部物质扩散,内部传热以及摩擦效应,例如由于机械功传递到系统或从系统传出而在系统内发生的粘度。如果有多个热流,则该术语[math]\displaystyle{ \dot{Q}/T }[/math]被替换为 [math]\displaystyle{ \sum \dot{Q}_j/T_j }[/math], 其中[math]\displaystyle{ \dot{Q}_j }[/math]是热流, [math]\displaystyle{ T_j }[/math]是进入系统的第j个热流端口的温度。
简单过程熵变公式
对于恒定组成系统中的某些简单过程,熵的变化可由简单的公式给出。[48]
理想气体等温膨胀或压缩
对于理想气体在任意温度下从初态[math]\displaystyle{ V_0 }[/math],[math]\displaystyle{ P_0 }[/math]到末态[math]\displaystyle{ V }[/math],[math]\displaystyle{ P }[/math]的膨胀(或压缩),熵为
[math]\displaystyle{ \Delta S = n R \ln \frac{V}{V_0} = - n R \ln \frac{P}{P_0} . }[/math]
这里n是气体的摩尔数,R是理想气体常数。这个公式也可以应用在有限真空的膨胀或焦耳-汤姆孙效应中,在这些过程中理想气体的温度、内能和焓不变。
制冷和制热
从初始温度[math]\displaystyle{ T_0 }[/math]开始以恒定压力加热或冷却任何系统(气体,液体或固体)到最终温度 [math]\displaystyle{ T }[/math],熵的变化是
[math]\displaystyle{ \Delta S = n C_P \ln \frac{T}{T_0}. }[/math]
假设恒压摩尔热容(或比热)[math]\displaystyle{ C_{P} }[/math]是恒定的,并且在此温度间隔内不发生相变。
类似的,在恒定体积下,熵变化为
[math]\displaystyle{ \Delta S = n C_V \ln \frac{T}{T_0} }[/math]
恒体积摩尔热容[math]\displaystyle{ C_V }[/math]恒定且没有相变。
在接近绝对零的低温下,固体的热容迅速下降至接近零,因此恒定热容的假设不适用。[49] 由于熵是状态函数,因此温度和体积都发生变化的任何过程的熵变化都与分为两步的路径相同-恒定体积加热和恒定温度膨胀。对于理想气体,总熵变为[50]
[math]\displaystyle{ \Delta S = nC_V \ln \frac{T}{T_0} + nR \ln \frac{V}{V_0}. }[/math]
同样,如果理想气体的温度和压力均发生变化,
[math]\displaystyle{ \Delta S = nC_P \ln \frac{T}{T_0} - nR \ln \frac{P}{P_0}. }[/math]
相变
在恒定的温度和压力下会发生可逆的相变。可逆热是跃迁的焓变,熵变是焓变除以热力学温度。[51]对于在熔点T m处固体与液体的熔化,熔化的熵为
[math]\displaystyle{ \Delta S_\text{fus} = \frac{\Delta H_\text{fus}}{T_\text{m}}. }[/math]
类似地,对于汽化在沸点的液体到气体的T b,所述汽化熵是:
[math]\displaystyle{ \Delta S_\text{vap} = \frac{\Delta H_\text{vap}}{T_\text{B}}. }[/math]
熵的理解方式
作为热力学和物理学的基本,除了Clausius和Boltzmann定义之外,还有几种不同的有效的熵表示方法。
教科书
下列是一系列教科书中熵的其他定义: 在特定温度下能量分散程度的量度。 衡量宇宙无序或衡量系统中对能做功的能量的一种度量。[52] 一种系统单位温度的不能用于做有用功的热能量度。[53] 在玻尔兹曼的定义中,熵是热力学平衡系统中可能的微观状态(或多个微观状态)数量的量度。与玻耳兹曼定义一致,热力学第二定律需要重新措词,以使熵随着时间的推移而增加,尽管基本原理保持不变。
有序和无序
熵经常不准确地与热力学系统中的顺序、随机或混乱程度相关联在一起。熵的传统定性描述是,它是指系统状态的变化,是对“分子无序”的一种度量,是动态能量从一种状态或一种状态转换为另一种状态时所浪费的能量的量。在这个方向上,最近的几位作者已经得出了精确的熵公式,以解释和测量原子和分子组分中的无序和有序。[54] [55] [56]较简单的熵序/无序公式之一是热力学物理学家Peter Landsberg于1984年基于热力学和信息理论的结合得出的。他认为,当约束在系统上运行时,与禁止状态相比,阻止其进入可能或允许的状态中的一个或多个状态,系统中“无序”总量的度量为:[55] [56]
[math]\displaystyle{ Disorder={C_\text{D}\over C_\text{I}}.\, }[/math]
同样,系统中“有序”的总量由下式给出:
[math]\displaystyle{ \text{Order}=1-{C_\text{O}\over C_\text{I}}.\, }[/math]
其中[math]\displaystyle{ C_\text{D} }[/math]是系统的“无序”容量,它是包含在允许的系综中的部分的熵,[math]\displaystyle{ C_\text{I} }[/math]是系统的“信息”容量,类似于Shannon的信道容量,以及[math]\displaystyle{ C_\text{O} }[/math]是系统的“有序”容量。[54]
能量传播
熵的概念可以定性地描述为特定温度下能量扩散的量度。[57]在经典热力学的历史早期就已经使用了类似的术语,并且随着统计热力学和量子理论的发展,已经通过混合或“散布”每种成分的总能量来描述熵的变化。系统在其特定的量化能级上的分布。 混乱(disorder)和混沌(chaos)一词中的歧义通常具有直接与均衡相反的含义,对大多数学生而言,它们造成了广泛的困惑并阻碍了对熵的理解。[58]如热力学第二定律所示,在一个孤立系统中,处于不同温度的内部趋向于调节至单个均匀温度,从而产生平衡。最近开发的一种教学方法方法避免了模棱两可的术语,并描述了这种能量的扩散,如分散,即使总能量根据热力学第一定律保持恒定,也导致工作所需的微分损失[59]。(比较下一节的讨论)。例如,物理化学家彼得·阿特金斯(Peter Atkins)以前曾写过分散导致无序状态的文章,现在写道“自发变化总是伴随着能量的分散”。[60]
将熵与能量有用性联系
根据以上所述,有可能(在热环境中)将较低的熵视为特定能量的有效性或有用性的指标或度量。[61]这是因为在较高温度下(即,具有较低的熵)提供的能量比在较低温度下提供的相同数量的能量更有用。将热的流体与冷的流体混合会产生一个中间温度的流体,其中熵的总体增加表示永远无法弥补的“损失”。 因此,宇宙的熵在稳步增加这一事实,意味着其总能量正在变得不那么有用:最终,这导致了“宇宙热寂学说”。[62]
熵和绝热程度
一种完全基于平衡状态之间的绝热可达性的熵的定义是埃利奥特·莱伯(Elliott H.Lieb)和雅各布·瓦森(Jakob Yngvason)在1999年[63]建立的。其中几项先驱工作,包括1909年Constantin Carathéodory开创性的工作和R. Giles的论文。[65]在Lieb和Yngvason的设定中,首先是对所考虑的单位物质,选择两个参考状态[math]\displaystyle{ X_0 }[/math]和 [math]\displaystyle{ X_1 }[/math],前者能绝热地到达后者但反之不成立。在此条件下的一个简单但重要的结果是,除了通过选择每个化学元素的单位和可加常数之外,还通过以下特性来唯一地确定熵:熵关于绝热可及性、复合系统的可加性以及广延扩展的关系而言单调递增。
量子力学中的熵
在量子统计力学中,熵的概念是由约翰·冯·诺依曼(John von Neumann)发展的,通常被称为“ 冯·诺依曼(von Neumann)熵 ”,
[math]\displaystyle{ S = - k_B\operatorname{Tr} ( \rho \log \rho ) \! }[/math]
其中ρ是密度矩阵,而Tr是迹算子。 这保持了对应原理,因为在经典极限中,当用于经典概率的基本状态之间的相位纯粹是随机的时,此表达式等同于熟悉的经典熵定义,
[math]\displaystyle{ S = - k_\mathrm{B}\sum_i p_i \, \log \, p_i, }[/math]
即在这样的基础上,密度矩阵是对角的。 冯·诺依曼(Von Neumann)的著作Mathematische Grundlagen der Quantenmechanik建立了严格的量子力学数学框架。他在这项工作中提供了一种测量理论,其中通常将波函数坍缩的概念描述为不可逆过程(所谓的冯·诺依曼或射影测量)。利用这个概念,结合密度矩阵,他将熵的经典概念扩展到了量子领域。
信息论
当从信息论的角度看时,状态函数熵只是指定系统的完整微观态所需的信息量(在香农的意义上)。宏观描述对此未作规定。 在信息论中,熵是接收之前丢失的信息量的量度,有时也称为香农熵。[67]香农熵是信息理论和最大熵热力学中广泛使用的一般概念。它最初是由克劳德·香农(Claude Shannon)于1948年设计的,用于研究传输消息中的信息量。但是,信息熵的定义相当笼统,用离散的概率[math]\displaystyle{ p_i }[/math]表示,有
[math]\displaystyle{ H(X) = -\sum_{i=1}^n p(x_i) \log p(x_i). }[/math]
在发送消息的情况下,这些概率是实际发送特定消息的概率,而消息系统的熵是对消息中平均信息量的度量。对于相等概率的情况(即,每条消息均具有同等概率),香农熵(以位为单位)只是确定消息内容所需的是/否问题的数量。[22]
信息熵和热力学熵之间的联系问题是一个有争议的话题。大多数作者认为两者之间有联系,[68] [69] [70] [71] [72]中有一些人认为它们之间没有任何关系。[73] 两个熵的表达式相似。如果w ^是微观的是可以产生一个给定的宏观态的数目,并且每个微态具有相同的先验概率,则该概率为p = 1 / W。香农熵(单位nats)是:
[math]\displaystyle{ H = -\sum_{i=1}^W p \log (p)= \log (W) }[/math]
如果以k / nat 为单位来衡量熵,那么熵可以通过以下公式给出[74]:
[math]\displaystyle{ H = k \log (W) }[/math]
当k是玻尔兹曼常数时,这就是著名的玻尔兹曼熵公式,这可以解释为每纳特的热力学熵。有许多种方法可以证明“信息熵”和“物理熵”的等价性,即“香农熵”和“玻尔兹曼熵”的等价性。然而,一些作者主张放弃信息论中H函数的熵一词,而改用Shannon的另一个术语“不确定性”。[75]
熵的实验测量
可以间接地测量物质的熵,尽管不是直接的。测量熵使用的温度定义[76],同时将能量交换限制为热量([math]\displaystyle{ dU \rightarrow dQ }[/math])。
[math]\displaystyle{ T := \left(\frac{\partial U}{\partial S}\right)_{V,N} \Rightarrow \cdots \Rightarrow \; dS=dQ/T }[/math]
结果关系描述了当少量的能量 [math]\displaystyle{ dS }[/math] 在一定温度T下被引入系统时,熵如何随[math]\displaystyle{ dQ }[/math] 变化。 测量过程如下。首先,将物质样品冷却至尽可能接近绝对零。在这样的温度下,由于温度的定义,熵接近零。然后,将少量热量引入样品中,并记录温度变化,直到温度达到所需值(通常为25°C)。所获得的数据使测量者可以对上述方程式进行积分,从而得出最终温度下物质熵的绝对值。熵的这个值称为量热熵。[77]
熵在其他领域应用
尽管熵的概念最初是一个热力学构造函数,但它已在其他研究领域进行了变形,包括信息论,心理动力学,热经济学 / 生态经济学和进化论。[54] [78] [79] [80] [81] 例如,最近提出了一种熵理论来解释洞穴蜘蛛在选择合适的产卵区域时的偏好。[82]
如果热力学熵表征能量耗散,那么摩擦疲劳熵表征其能量吸收。[83] [84]其变化由公式给出
[math]\displaystyle{ (d_i S)_{TF} = \frac{\gamma_1^{(w)}}{T_\Sigma} \omega_\Sigma dV_{P\gamma}. }[/math]
根据该式,摩擦疲劳熵是通过不可逆的损伤引起ω Σ在危险的体积V p γ移动和可变形固体的,彼此和/或与该介质相互作用。这里Ť p γ ≥ Ť是由所有来源(使温度Ť是介质的温度),γ 1 (ω)是压力(应力),这导致为单个值的危险体积损坏。
根据广义概念(例如,参见[85] [86] [87] [88]),损坏是成分,结构,结构,尺寸,形状,体积,质量(等)的不可逆转的变化,因此,对象的相应理化,力学等性能;最终,损害与破坏身体的连续性和完整性有关,直至破坏(例如分解为原子)。因此,损坏被解释为移动和可变形系统的基本属性(和义务)。
不可逆的损害(ω的复合物(Σ)Σ)由有效(在系统吸收)能量来确定(û Σ (EFF)),引起的任何性质的力:
[math]\displaystyle{ \omega_\Sigma(U_\Sigma^\mathit{eff}) = \omega_\Sigma \left(U_n^\mathit{eff}, U_\tau^\mathit{eff}, U_T^\mathit{eff}, U_{ch}^\mathit{eff}, \ldots, U_0, t \right) = \omega_{\Sigma U} \ge 0 }[/math]
在这里,指数n和τ表示法向和剪切机械载荷,T和Ch表示产生相应能量通量的热和电化学载荷。
因此,损坏ω Σ是一种能量的热机械功能,因为它考虑到两者的任何力因子和温度Ť Σ。这意味着摩擦疲劳熵是所有源引起的能量吸收的量度。测定程序ù Σ (EFF)已经被开发(见,例如。[85] [86] [87] [88] [89]
对物体的物理损害的空间条件成立,[86]其中指出:不可逆的损伤进程的发展是可能的,并且被实现以一定的概率Р > 0,当一个有限区域V p γ与有效非零电平能量ù Σ (EFF) > 0(内部熵š 我 > 0)发生在对象-一个危险的体积
[math]\displaystyle{ V_{P\gamma} \in V_{P\gamma} \left(Q_i, U_\Sigma^\mathit{eff}, S_i\right) \ge 0, }[/math]
其中Qi -是内力因素。
如果V p γ = 0,则ω Σ = 0,因此,由一个损伤对象的演变是impossi-BLE(可逆系统)。以不可逆的系统V p γ ≤ V有其空间损伤的绝对值(测定)(V是其几何体积)。计算方法和危险的体积(的分类V p γ)为典型的物质对象(可变形的固体和系统)在各种条件下,已经开发(见,例如。[87]系统损伤的规模可以是任何。
使用摩擦疲劳熵的概念,可以对损伤进行熵解释:对物体的不可逆损伤等同于其内部熵在其危险体积中的变化。
[math]\displaystyle{ \omega_\Sigma(S_{TF}) \equiv \frac{(d_i S)_{TF}}{dV_{P\gamma}} = \omega_{\Sigma S}. }[/math]
一个开放的热力学系统(其中损坏的或固体的物体分布(分散))称为机械热力学系统(MTD)。如图[89] [90]所示,这种系统中熵的变化取决于热力学(TD指数)和摩擦疲劳(TF指数)熵的函数:
[math]\displaystyle{ \begin{align} dS_{MTD} &= \left[(dS)_{TD} \rightleftarrows (d_i S)_{TF}\right] \\ &= \Lambda_{TD\backslash TF} \left[\left(\frac{dU + p\,dV}{T} - \frac{1}{T}\sum_1^n{\mu\,dN_k}\right)_{TD} + \left(\gamma_1^{(w)}\frac{\omega_\Sigma}{T_\Sigma}dV_{P\gamma}\right)_{TF} \right] \uparrow , \Lambda \lesseqgtr 1. \\ \end{align} }[/math]
该方程式允许分析系统的任何(可能的)状态。他认为,由于系统的热机械状态,摩擦疲劳熵的增加会导致移动和可变形的物体和系统的破坏和分解。在热力学方程中,这样的状态是不可能的。考虑到熵分量之间相互作用的各种机制来构造该方程式。
因此,从前面的内容可以得出,在一般情况下,系统的演化取决于熵不可逆变化的过程强度-热力学和摩擦疲劳;内部机械热力学熵的产生与运动和破坏一样永恒。
热力学和统计力学相关概念
熵单位–热力学熵的非SI单位,通常表示为“ eu”,等于每摩尔每开尔文一个卡路里,或每摩尔每开尔文4.184 焦耳。[91]
吉布斯熵 –热力学系统通常的统计机械熵。
Boltzmann熵 –一种Gibbs熵,在整体粒子分布中忽略了内部统计相关性。
Tsallis熵 –标准Boltzmann–Gibbs熵的推广。
标准摩尔熵 –是在标准温度和压力条件下,一摩尔物质的熵含量。
残留熵 –物质任意冷却到绝对零附近后存在的熵。
混合熵 –两种不同化学物质或成分混合时的熵变。
环熵 –是在规定距离内将聚合物的两个残基聚集在一起而损失的熵。
构象熵 –是与聚合物链的物理排列相关的熵,聚合物链在溶液中呈致密或球形状态。
熵力 –与系统组织变化,分子摩擦考虑和统计变化有关的微观力或反应趋势。
自由熵 –类似于自由能的熵热力学势。
熵爆炸 -爆炸,其中反应物的体积发生较大变化而不会释放大量热量。
熵变– 两个平衡状态之间的熵dS的变化由传热dQ rev除以该间隔内系统的绝对温度T给出。
Sackur-Tetrode熵 -通过量子考虑确定的单原子经典理想气体的熵。
时间之箭
熵是物理学中唯一提及会向特定发展方向的量,有时被称为时间之箭。随着时间的流逝,热力学第二定律指出,在大型系统中,孤立的系统的熵在相当长的一段时间内不会减少。因此,从这个角度来看,在这些条件下,熵测量被认为是时钟。
DNA序列中的熵
熵被证明可用于DNA序列分析。一些研究表示,出许多基于熵的度量可以区分基因组的不同结构区域,区分DNA的编码区域和非编码区域,并且还可以通过确定不同物种之间的进化距离来应用于重建进化树。[92]
宇宙学
由于有限宇宙是一个孤立的系统,因此热力学第二定律指出其总熵在不断增加。据推测,自19世纪以来,宇宙注定要经历热寂,在热寂中,所有能量最终以热能的均匀分布结束,因此无法从任何来源提取更多的功。 如果可以认为宇宙总体上具有熵的增加,那么正如罗杰·彭罗斯(Roger Penrose)所指出的那样,重力在该过程中起着重要作用,因为重力会使分散的物质积聚成恒星,最终坍塌成黑洞。黑洞的熵与黑洞的事件视界的表面积成正比。[93] [94] [95] 雅各布·贝肯斯坦(acob David Bekenstein)和史蒂芬·霍金(Stephen Hawking)证明了在任何大小相等的物体中,黑洞具有最大的熵。如果它们是完全有效的物质和能量陷阱,则它们可能是所有熵增加过程的终点。[96]然而,由于量子活性,能量可能会从黑洞中逸出(见霍金辐射)。
自Ludwig Boltzmann时代以来,熵在宇宙学中的作用仍然是一个有争议的话题。最近的工作使人们对热寂假说以及任何简单的热力学模型在宇宙的普遍适用性产生了怀疑。尽管在扩展的宇宙模型中熵确实增加了,但最大可能的熵却增长得更快,随着时间的推移,使宇宙离热寂的距离越来越远,而不是越来越近。[97] [98] [99] 这导致“熵间隙”,使系统进一步远离假定的热死平衡。[100]其他复杂因素,例如真空的能量密度和宏观量子这种效应很难与热力学模型相吻合,因此热力学对大型系统的任何预测都极为困难。[101]
当前的理论表明,熵间隙最初是由宇宙的早期快速指数膨胀所打开的。[102]
经济学
罗马尼亚裔美国经济学家尼古拉斯·乔治斯丘·罗根(Nicholas Georgescu Roegen),一个在经济学领域创办生态经济模式的先驱,他大量使用了熵的概念,得到了著名的熵定律和经济过程。[69]由于Georgescu Roegen的工作,热力学定律现在已成为生态经济学派的组成部分。[103] [104]尽管他的工作因错误而有些瑕疵,但一些书中有关热力学历史发展的基本物理学教科书中已包含一整篇有关乔治斯库-罗根经济学的章节。[105]
在经济学上,Georgescu Roegen的著作产生了“熵悲观主义”一词。[106]:116自1990年代以来,领先的生态经济学家和稳态理论家赫尔曼·戴利( Herman Daly,Georgescu Roegen的学生)一直是经济学界对熵悲观主义立场最有影响力的支持者。[107][108]
诠释学
在诠释学中,Arianna Béatrice Fabbricatore使用了依赖于安伯托·艾柯(Umberto Eco)的著作[109]的术语来识别和评估舞蹈的口头描述与舞蹈文本(舞者穿上时动的丝绸)之间的意义损失。由符号间翻译操作实现舞蹈作品[110]的产生。[111] [112]
此用法与徽标文本和编排文本的概念相关。在从徽标文本到舞蹈文本的过渡中,可以确定两种熵类型:第一种称为“自然”,与表演行为的独特性及其短暂性有关。第二种是由徽标文本(即反映所跳动动作的口头文本)中或多或少重要的“空洞”引起的[113]。
编者推荐
- 参考资料:维基百科 熵
下是关于集智俱乐部关于社团结构的一些文章
本中文词条由Gravity PHY用户参与编译, 刘佩佩 用户审校,Meng莫编辑,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。