临界点(热力学)
在热力学中,一个临界点 Critical point(或临界状态)就是相平衡曲线的终点。最突出的例子是液-汽临界点,即压力-温度曲线的终点,它指明了液体和其蒸汽可以共存的条件。温度再高,气体就不能单靠压力液化。在由临界温度Tc和临界压力pc定义的临界点,相边界消失。其他例子包括混合物中的液-液临界点。
液-汽临界点
总览
为使表述简单明晰,临界点的一般概念最好通过讨论一个具体的例子,液体-蒸汽临界点,来介绍。这是第一个被发现的临界点,也仍然是最著名和被研究最多的一个。
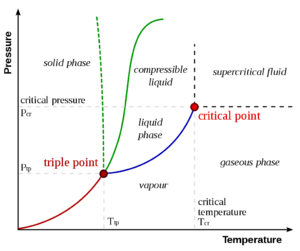
右图显示了纯物质的PT示意图(与混合物相反,混合物具有额外的状态变量和更丰富的相图,如下所述)。众所周知的固相、液相和汽相通过相边界分离,即两相可以共存的压力-温度组合。在三相点,所有三个相可以共存。然而,在临界温度Tc和临界压力 pc时,液-汽边界终止于一个端点。这便是临界点。
在水中,临界点出现在 647.096 K(373.946 °C;705.103 °F)和 22.064 兆帕(3,200.1 psi;217.75 atm)。.[1]
在临界点附近,液体和蒸汽的物理性质发生了巨大变化,两相变得越来越相似。例如,液态水在正常条件下几乎不可压缩,热膨胀系数低,介电常数高,是电解质的优良溶剂。在临界点附近,所有这些特性都变成完全相反的:水变得可压缩、可膨胀、介电性差、电解质的不良溶剂,并且更喜欢与非极性气体和有机分子混合。[2]
在临界点,只有一个相存在。汽化热为零。在PV图上的恒温线(临界等温线 Critical isotherm)中有一个固定的拐点。这意味着在临界点:[3][4][5]
- [math]\displaystyle{ \left(\frac{\partial p}{\partial V}\right)_T = 0, }[/math]
- [math]\displaystyle{ \left(\frac{\partial^2p}{\partial V^2}\right)_T = 0. }[/math]
在临界点以上存在一种物质状态,它与液态和气态连续相连(无相变即可转化)。它被称为超临界流体 supercritical fluid。关于液体和蒸汽之间的所有区别都在临界点之外消失的共同教科书知识受到了Michael Fisher和Benjamin Widom的质疑,[6]他们确定了一条p-T线,它分开了具有不同渐近统计性质的状态(Fisher-Widom线)。
有时,临界点并不表现在大多数热力学或机械性质上,而是隐藏在弹性模量的不均匀性开始、非仿射液滴的外观和局部特性的显著变化以及缺陷对浓度的突然增强中。在这些情况下,我们会有一个隐藏的临界点,否则我们就有一个暴露的临界点。 [7]
历史
临界点的存在于 1822 年由Charles Cagniard de la Tour [8][9]首次发现,并由Dmitri Mendeleev在 1860 年[10][11]和Thomas Andrews在 1869年命名。[12]Cagniard 表明 CO2可以在 31 °C 和 73 atm 的压力下液化,但不能在稍高的温度下液化,即使在高达 3000 atm 的压力下也是如此。
理论
解决对于van der Waals方程的上述条件[math]\displaystyle{ (\partial p / \partial V)_T = 0 }[/math],就能将临界点计算为
- [math]\displaystyle{ T_\text{c} = \frac{8a}{27Rb}, \quad V_\text{c} = 3nb, \quad p_\text{c} = \frac{a}{27b^2}. }[/math]
然而,基于平均场理论的van der Waals方程在临界点附近不成立。特别是,它预测了错误的标度定律。为分析接近临界点的液体的性质,还原态变量有时会被相对于临界性质定义:[13]
- [math]\displaystyle{ T_\text{r} = \frac{T}{T_\text{c}}, \quad p_\text{r} = \frac{p}{p_\text{c}}, \quad V_\text{r} = \frac{V}{RT_\text{c} / p_\text{c}}. }[/math]
对应态原理表明,在相同的减压和温度下,物质具有相等的还原体积。这种关系对于许多物质来说几乎是正确的,但是对于pr的大值,这种关系变得越来越不准确。
对于某些气体,在以这种方式计算的临界温度和临界压力上,还有一个额外的修正系数,叫做牛顿修正。这些是根据经验得出的值,并随感兴趣的压力范围而变化。[14]
部分物质的液-气临界温度和压力表
| Substance[15][16] | Critical temperature | Critical pressure (absolute) |
|---|---|---|
| 氩气 | −122.4 °C (150.8 K) | 48.1 atm (4,870 kPa) |
| 氨(NH3[17] | 132.4 °C (405.5 K) | 111.3 atm (11,280 kPa) |
| R-134a | 101.06 °C (374.21 K) | 40.06 atm (4,059 kPa) |
| R-410A | 72.8 °C (345.9 K) | 47.08 atm (4,770 kPa) |
| 溴 | 310.8 °C (584.0 K) | 102 atm (10,300 kPa) |
| 铯 | 1,664.85 °C (1,938.00 K) | 94 atm (9,500 kPa) |
| 氯气 | 143.8 °C (416.9 K) | 76.0 atm (7,700 kPa) |
| 乙醇 (C2H5OH) | 241 °C (514 K) | 62.18 atm (6,300 kPa) |
| 氟 | −128.85 °C (144.30 K) | 51.5 atm (5,220 kPa) |
| 氦气 | −267.96 °C (5.19 K) | 2.24 atm (227 kPa) |
| 氢气 | −239.95 °C (33.20 K) | 12.8 atm (1,300 kPa) |
| 氪 | −63.8 °C (209.3 K) 54.3 atm (5,500 kPa) | 54.3 atm (5,500 kPa) |
| 甲烷(CH4) | −82.3 °C (190.8 K) | 45.79 atm (4,640 kPa) |
| 氖 | −228.75 °C (44.40 K) 27.2 atm (2,760 kPa) | 27.2 atm (2,760 kPa) |
| 氮气 | −146.9 °C (126.2 K) | 33.5 atm (3,390 kPa) |
| 氧气(O2) | −118.6 °C (154.6 K) | 49.8 atm (5,050 kPa) |
| 二氧化碳 (CO2) | 31.04 °C (304.19 K) | 72.8 atm (7,380 kPa) |
| 氧化亚氮(N2O) | 36.4 °C (309.5 K) | 71.5 atm (7,240 kPa) |
| 硫酸(H2SO4) | 654 °C (927 K) | 45.4 atm (4,600 kPa) |
| 氙气 | 16.6 °C (289.8 K) | 57.6 atm (5,840 kPa) |
| 锂 | 2,950 °C (3,220 K) | 652 atm (66,100 kPa) |
| 汞 | 1,476.9 °C (1,750.1 K) | 1,720 atm (174,000 kPa) |
| 硫 | 1,040.85 °C (1,314.00 K) | 207 atm (21,000 kPa) |
| 铁 | 8,227 °C (8,500 K) | |
| 金 | 6,977 °C (7,250 K) | 5,000 atm (510,000 kPa) |
| 铝 | 7,577 °C (7,850 K) | |
| 水 (H2O)[1][18] | 373.946 °C (647.096 K) | 217.7 atm (22,060 kPa) |
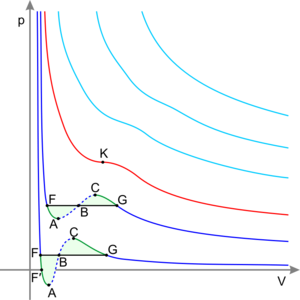
从理论上讲,液-液临界点代表旋节曲线的温度-浓度极值(如右图所示)。因此,双组分体系的液-液临界点必须满足两个条件:旋节曲线的条件(自由能对浓度的二阶导数必须等于零),以及极值条件(自由能对浓度的三阶导数也必须等于零,或者旋节温度对浓度的导数必须等于零)
混合物:液体-液体临界点
在“临界溶液温度”下,溶液的液-液临界点出现在相图两相区的极限处。换言之,它是某个热力学变量(如温度或压力)的微小变化导致混合物分离为两个不同的液相的点,如右侧的聚合物-溶剂相图所示。两种类型的液-液临界点是上临界溶液温度 upper critical solution temperature(UCST),这是冷却导致相分离的最热点,和下临界溶液温度 lower critical solution temperature(LCST)',这是加热导致相分离的最冷点。
数学定义
从理论上看,从液体的临界点(从理论上看,是指液体的临界温度)。因此,双组分体系中的液-液临界点必须满足两个条件:旋节曲线的条件(Gibbs自由能相对于浓度的“二阶”导数必须等于零)和极值条件(自由能相对于浓度的“第三”导数)也必须等于零,或者旋节温度对浓度的导数必须等于零)。
参见
- 共形场论 Conformal field theory
- 临界指数 Critical exponents
- 临界现象 Critical phenomena
- 要素临界点 Critical points of the elements (data page)
- 居里点 Curie point
- 液体-液体临界点 Liquid–liquid critical point
- Néel点 Néel point
- 过滤阈值 Percolation thresholds]]
- 相变
- Rushbrooke不等式 Rushbrooke inequality
- 比例不变性 Scale invariance
- 自组织临界性
- Widom缩放 Widom scaling
参考文献
- ↑ 1.0 1.1 Wagner, W.; Pruß, A. (June 2002). "The IAPWS Formulation 1995 for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use". Journal of Physical and Chemical Reference Data. 31 (2): 398. doi:10.1063/1.1461829.
- ↑ Anisimov, Sengers, Levelt Sengers (2004):Near-critical behavior of aqueous systems. Chapter 2 in Aqueous System at Elevated Temperatures and Pressures Palmer et al., eds. Elsevier.
- ↑ P. Atkins and J. de Paula, Physical Chemistry, 8th ed. (W. H. Freeman 2006), p. 21.
- ↑ K. J. Laidler and J. H. Meiser, Physical Chemistry (Benjamin/Cummings 1982), p. 27.
- ↑ P. A. Rock, Chemical Thermodynamics (MacMillan 1969), p. 123.
- ↑ Fisher, Widom: Decay of Correlations in Linear Systems, J. Chem. Phys. 50, 3756 (1969).
- ↑ Das, Tamoghna; Ganguly, Saswati; Sengupta, Surajit; Rao, Madan (3 June 2015). "Pre-Yield Non-Affine Fluctuations and A Hidden Critical Point in Strained Crystals". Scientific Reports. 5 (1): 10644. Bibcode:2015NatSR...510644D. doi:10.1038/srep10644. PMC 4454149. PMID 26039380.
- ↑ Charles Cagniard de la Tour (1822). "Exposé de quelques résultats obtenu par l'action combinée de la chaleur et de la compression sur certains liquides, tels que l'eau, l'alcool, l'éther sulfurique et l'essence de pétrole rectifiée". Annales de Chimie et de Physique (in français). 21: 127–132.
- ↑ Berche, B., Henkel, M., Kenna, R (2009) Critical phenomena: 150 years since Cagniard de la Tour. Journal of Physical Studies 13 (3), pp. 3001-1–3001-4.
- ↑ Mendeleev called the critical point the "absolute temperature of boiling".
- Менделеев, Д. (1861). "О расширении жидкостей от нагревания выше температуры кипения" [On the expansion of liquids from heating above the temperature of boiling]. Горный Журнал [Mining Journal] (in русский). 4: 141–152. The "absolute temperature of boiling" is defined on p. 151. Available at Wikimedia
- Mendelejeff, D. (1861). "Ueber die Ausdehnung der Flüssigkeiten beim Erwärmen über ihren Siedepunkt" [On the expansion of fluids during heating above their boiling point]. Annalen der Chemie und Pharmacie (in Deutsch). 119: 1–11. doi:10.1002/jlac.18611190102.
- 1870 年,Mendeleev反对Thomas Andrews,主张他优先考虑临界点的定义。Mendelejeff, D. (1870). "Bemerkungen zu den Untersuchungen von Andrews über die Compressibilität der Kohlensäure" [Comments on Andrews' investigations into the compressibility of carbon dioxide]. Annalen der Physik. 2nd series (in Deutsch). 141: 618–626. doi:10.1002/andp.18702171218.
- ↑ Landau, Lifshitz, Theoretical Physics, Vol. V: Statistical Physics, Ch. 83 [German edition 1984].
- ↑ Andrews, Thomas (1869). "The Bakerian lecture: On the continuity of the gaseous and liquid states of matter". Philosophical Transactions of the Royal Society. London. 159: 575–590. doi:10.1098/rstl.1869.0021. The term "critical point" appears on page 588.
- ↑ Cengel, Yunus A.; Boles, Michael A. (2002). Thermodynamics: an engineering approach. Boston: McGraw-Hill. pp. 91–93. ISBN 978-0-07-121688-3.
- ↑ Maslan, Frank D.; Littman, Theodore M. (1953). "Compressibility Chart for Hydrogen and Inert Gases". Ind. Eng. Chem. 45 (7): 1566–1568. doi:10.1021/ie50523a054.
- ↑ Emsley, John (1991). The Elements (Second ed.). Oxford University Press. ISBN 978-0-19-855818-7.
- ↑ Cengel, Yunus A.; Boles, Michael A. (2002). Thermodynamics: An Engineering Approach (Fourth ed.). McGraw-Hill. pp. 824. ISBN 978-0-07-238332-4. https://archive.org/details/thermodynamicsen00ceng_0/page/824.
- ↑ "Ammonia - NH3 - Thermodynamic Properties". www.engineeringtoolbox.com. Retrieved 2017-04-07.
- ↑ "Critical Temperature and Pressure". Purdue University. Retrieved 2006-12-19.
- "Revised Release on the IAPWS Industrial Formulation 1997 for the Thermodynamic Properties of Water and Steam" (PDF). International Association for the Properties of Water and Steam. August 2007. Retrieved 2009-06-09.
外部链接
- "Critical points for some common solvents". ProSciTech. Archived from the original on 2008-01-31.
- "Critical Temperature and Pressure". Department of Chemistry. Purdue University. Retrieved 2006-12-03.
编者推荐
集智课程
复杂性与临界现象 2020
该课程为北京师范大学系统科学学院陈晓松教授开设的研究生课程《复杂性与临界现象》课程回放。
主要讲解内容:
- 复杂系统与复杂性简介
- 统计系统理论
- 平衡态系统临界现象
- 非平衡与复杂系统临界现象
平衡态系统相变临界现象
目前临界在平衡态系统的研究比较成熟,本节课程将对过去一百多年的关于相变临界现象的研究进行介绍,其研究思想、方法、观点、概念,对其他非平衡态系统、动力系统的研究也有借鉴意义。
主要讲解内容:
- 平衡态临界现象的根本特征是长程关联
- 系统的宏观性质具有标度性和普适性
- 描述系统宏观性质的临界指数只依赖系统维数和序参量的维数
- 在平均场近似下,不同空间维数系统的临界指数相同
临界现象的标度性与超标度关系
在物理学中,精确解具有重要的意义。该课程将从与临界涨落相关的热力学量自由能,其奇异部分满足齐次性要求下,求解推出临界现象的标度性与超标度关系,得出一般性规律。
主要讲解内容:
- 由自由能奇异部分的齐次性,可将所有临界指数用关联长度的临界指数表示
- 关联长度有对温度和外场两个临界指数
- 各热力学量的临界指数并不独立,满足超标度(hyperscaling)关系
- 临界现象理论得到了微重力、高精度实验的证实
本中文词条由Henry翻译,Miyasaki审校,薄荷编辑,如有问题,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。