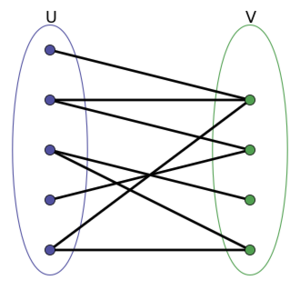
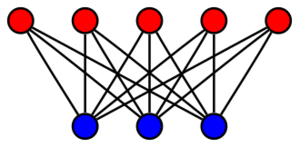
二分图
在图论的数学领域中,二分图 Bipartite graph(或二部图)是一个曲线图,其所有顶点可以分为两个互不相交且独立的集合[math]\displaystyle{ U }[/math]和集合[math]\displaystyle{ V }[/math],并且邻边(无向或有向)的两个顶点分别属于集合[math]\displaystyle{ U }[/math]和集合[math]\displaystyle{ V }[/math]。通常集合[math]\displaystyle{ U }[/math]和集合[math]\displaystyle{ V }[/math]被称为该二分图的子集。同时,二分图中不包含任何形式的奇数环,即:集合[math]\displaystyle{ U }[/math]和集合[math]\displaystyle{ V }[/math]构造的点集所形成的循环圈边数不为奇数。[1][2]
通常可以将集合[math]\displaystyle{ U }[/math]和集合[math]\displaystyle{ V }[/math]视为被着色的两个图集:如果其中一个所有顶点为蓝色,另外一类为绿色,那么每条连边的两端必须具有不同的颜色。这是二分图必须满足的条件。[3][4]相反,在非二分图(例如三角形)的情况下,这种着色要求是不可能的:因为如果一个顶点为蓝色,另一个为绿色,那么其剩下的第三个顶点将需要同时连接这两个颜色,显然这是不成立的,因为它违背了初始要求:二分图中所有顶点必须分为两个不相交且独立的集合[math]\displaystyle{ U }[/math]和[math]\displaystyle{ V }[/math]。即第三个顶点必须与另外两个点中的任意一个颜色相同。
对于二分图常用的表达方式是[math]\displaystyle{ G=(U,V,E) }[/math],其中[math]\displaystyle{ U }[/math]和[math]\displaystyle{ V }[/math]分别代表顶点子集,[math]\displaystyle{ E }[/math]代表二分图中的连边。如果有一个二分图内部不连通,那么它可能具有多个二分图;[5]在这种情况下,[math]\displaystyle{ (U,V,E) }[/math]标注将有助于指定一个特殊的二分图。在实际的应用当中这一点是很重要的。如果[math]\displaystyle{ |U|=|V| }[/math],即这两个子集具有相同的基数,此时[math]\displaystyle{ G }[/math]被称为均衡二分图 Balanced bipartite graph。如果在二分图中同一侧(同一个子集)所有的顶点都具有相同的度数,则[math]\displaystyle{ G }[/math]被称为双正则二分图 Biregular。
案例
在建立两类不同对象之间的关系时,人们常常会很自然地选择二分图。以建立足球运动员和俱乐部的关系图为例,如果该球员曾为该俱乐部效力,那么在运动员和俱乐部之间就形成了一条边。这是二分图在建立隶属关系网络中的应用示例。在社交网络分析中,隶属关系便形成一种二分图。[6]
自觉选用二分图的另一个例子是(NP-完全问题)铁路优化问题,其中输入项是火车的时间表及其停靠点,目标是找到尽可能小的火车站集合,以便每个火车都可以停靠至少一个选定的火车站。我们可以运用建模将这个问题转化为一个二分图中的主导集合问题,该图中每辆列车和每个车站都被看作是一个顶点,而当某列车停靠在某车站的时候,它们所形成的关系可看作一条连边。[7]
第三个例子涉及到货币金融学领域。古代的硬币被设计为正反两面,不同时期和地区的政府会使用不同的正反面组合,因此,将所有可能的组合画成图就是一个二分图的结构。[8]
更多抽象的例子:
- 每个树状图都是二分的。[3]
- 具有偶数个顶点的环图都是二分的。[3]
- 在平面图中,所有面都具有偶数条边,该图为二分图。特殊情况是网格图和方图,其中每个内面都有4个边,每个内顶点至少有4个相邻点。
- 在一个完全二分图中,分别由m和n的顶点(用Km,n表示)组成的两个不相交的集合U和V,连边E由分别在集合U和V的两个顶点连接。该二分图表示为G =(U,V,E),并且具有mn条边。另外完全二分图还有一个特例,那就是 冠图 Crown graphs。冠图是将一个完全二分图中所有的完美匹配连边去掉后形成的。[9]
- 超立方体图 Hypercube graph, 局部立方体 Partial cube和 中位数图 Median graph均为二分图。判别方法是将这些图中的顶点用 位向量Bitvector(二进制位组成的向量)进行标记,然后对比其中两个顶点的位向量,发现当且仅当位向量中只有一个位元是不同的时候,该两个顶点相邻。另外判定该图的二分性可以通过观察每个顶点的位向量,奇数位向量和偶数位向量分别为该图的二分顶点子集。树状图和方图都是中位数图,而所有中位数图都是局部立方体。[10]
属性
特征表述
二分图可以用以下几种不同的方式来描述其特征:
- 当且仅当它不包含奇数环的时候,该图为二分图。
- 当且仅当图是它是2-可着色的(即其色数小于或等于2)时,该图为二分图。[11]
- 一个图是二部图当且仅当它的顶点集 [math]\displaystyle{ V }[/math]可分为2个集合 [math]\displaystyle{ A }[/math]和[math]\displaystyle{ B }[/math],以至于[math]\displaystyle{ \sum_{v \in A} \deg(v) = \sum_{v \in B} \deg(v) }[/math], [math]\displaystyle{ \forall v \in A \deg(v) \leq |B| }[/math] 和[math]\displaystyle{ \forall v \in B \deg(v) \leq |A| }[/math]
- 任何由以下组成的二部图 [math]\displaystyle{ n }[/math] 顶点最多可以有 [math]\displaystyle{ n^2 / 4 }[/math]边缘。
- 当且仅当它是二分图时,图的频谱是对称的。[12]
柯尼希定理和完美图 Kőnig's theorem and perfect graphs
在二分图中, 最小顶点覆盖 Minimum vertex cover(顶点数)等于 最大匹配数 Maximum matching(边数);这就是 柯尼希定理 Kőnig's theorem。[13][14] 该定理的另一种等价形式是, 最大独立集 Maximum independent set(顶点数)加上最大匹配数等于顶点的数量。在任意没有孤立顶点的图中, 最小边覆盖 Minimum edge cover(边数)加上最大匹配数等于顶点数。[15]于是,将以上等式与柯尼希定理相结合,得出以下事实:在二分图中,最小边覆盖数值等于最大独立集数值,最小边覆盖数值加上最小顶点覆盖数值等于顶点数。
另一类相关特性与 完美图 Perfect graph有关:每个二分图及其补图、线图、线图的补图均为完美图。其实关于二分图的完美性很容易就可以看出来(它们的色数为2,最大的团数同样为2),但是二分图的补图完美性的判定更简单些,且可以看作是柯尼希定理的另一种表述。其实在定义完美图这一概念的初期,它是作为其中之一的论证结果而存在的。[16] 同时完美图线图的补图完美性也是作为柯尼希定理的另一种表述,线图的完美性陈述了比较早期的柯尼希定理,即每一个二分图的着色边,其色数都等于其最大节点度数。
根据 强完美图定理 Strong perfect graph theorem,完美图具有类似于二分图的 禁止图特征 Forbidden graph characterization:当且仅当它没有奇环的子图时,图才是二分的;当且仅当它没有奇环或其补图作为 导出子图Induced subgraph时,图才是完美的。二分图及其线图、补图占据了完美图五种基本类别中的四个,它们可以用于证明了强完美图定理。[17]
度相关问题
对于一个顶点,其相邻顶点的数量称为该顶点的度数,并表示为[math]\displaystyle{ \deg(v) }[/math]。二分图的总度数和公式为:
- [math]\displaystyle{ \sum_{v \in V} \deg(v) = \sum_{u \in U} \deg(u) = |E|\, . }[/math]
一个二分图的度数序列是一对列表,每个列表包含两个部分[math]\displaystyle{ U }[/math]和[math]\displaystyle{ V }[/math]的度数。例如,完全二分图K3,5具有度数序列 [math]\displaystyle{ (5,5,5),(3,3,3,3,3) }[/math]。其同构二分图 Isomorphic bipartite graphs具有相同的度数序列。但是,度数序列通常不是定义二分图的唯一方法;在某些情况下,非同构二分图可能具有相同的度数序列。
二分实现问题 Bipartite realization problem是通过以已知的两组自然数序列作为度数序列,来查找简单的二分图的判定问题(数理逻辑)。(尾随零可以忽略,因为通过向图添加适当数量的孤立顶点可以实现尾随为零。)
与超图和有向图的关系
一个二分图[math]\displaystyle{ (U,V,E) }[/math]的双邻矩阵是大小为[math]\displaystyle{ |U|\times|V| }[/math]的(0,1)矩阵,其分别代表了每对相邻顶点集合和非相邻顶点的集合(全零矩阵)。[18]双邻接矩阵可用于描述二分图,超图和定向图之间的等价关系。
超图是一种类似于无向图的组合结构。它具有顶点和连边,但是其中的边可以是任意子集组的顶点,而不必具有两个端点。可以使用二分图[math]\displaystyle{ (U,V,E) }[/math]来建模超图,其中[math]\displaystyle{ U }[/math]是超图的其中一个顶点集,[math]\displaystyle{ V }[/math]是该超图的连边集(称为超边集),[math]\displaystyle{ E }[/math]包含的连边定义为:从一个超图顶点[math]\displaystyle{ v }[/math]到超图连边[math]\displaystyle{ e }[/math]恰好当[math]\displaystyle{ v }[/math]是[math]\displaystyle{ e }[/math]的端点集之一时。在这种对应关系下,二分图的双邻矩阵正好是其相应超图的关联矩阵。作为二分图和超图之间这种对应关系的特例,任何 多重图 Multigraph(即在相同两点之间可能存在的多条边的图)都可以解释为其中一些超边具有相同端点集的超图,并且由不具有多个邻接关系的二分图表示,其中二分图的同边顶点的度数均为2。[19]
关于邻接矩阵的另一个相似解释可以被用于展示有向图和均衡二分图(二分子集顶点数相等)之间的一一对应关系(在给定数量的标记顶点上,允许自循环)。例如,具有[math]\displaystyle{ n }[/math]个顶点的有向图的邻接矩阵可以是大小为[math]\displaystyle{ n\times n }[/math]的任何(0,1)矩阵,然后可以将其重新解释为:具有相同顶点数[math]\displaystyle{ n }[/math]的同边子集的二分图的邻接矩阵。[20]通过这种构建方式,二分图可以被解释为是一个有向图的 二分双重覆盖 Bipartite double cover。
算法
二分性测试
可以使用 深度优先搜索 Depth-first search来测试图是否为二分图,并在线性时间内返回双色(如果是二分图)或奇数环(如果不是二分图)。其方法的主要思想是为每个顶点分配与 深度优先搜索林 Depth-first search forest中其上级颜色不同的颜色,并在其中进行全部选择。这必定会为生成林 Spanning forest提供两种颜色,包括将顶点连接到其上级的边。不过它可能无法为非林边正确着色。在深度优先搜索林中,每个非林边缘的两个顶点之一是另一个顶点的始源,并且当深度优先搜索发现这种类型的边时,应检查这两个顶点是否具有不同的颜色。如果不是,则林中从始源到后代的路径与颜色不同的边一起会形成一个奇数环,该奇数环会从算法中返回,并输出非二分图的结果。但是,如果算法在未检测到此类奇数环的情况下终止,则必须对每个边进行适当的着色,并返回双色以及得出该图形为二分图的结果。[21]
又或者,可以使用 广度优先搜索 Breadth-first search来替代深度优先搜索进行检测。同样,在搜索林中,以广度优先的顺序为每个节点赋予与上级节点相反的颜色。如果在着色某个顶点时存在一条边,其连接了与先前着色的顶点相同的颜色。然后这条边沿着以广度优先搜索林中的路径,将其两个端点与其最低共有始源nLowest common ancestor相连,形成一条奇数环。当然,如果该算法最终没找到奇数环且终止,那么它肯定已经找到了正确的着色,可以安全返回并得出该图是二分图的结论。[22]
对于[math]\displaystyle{ n }[/math]个线段的相交图或 欧几里得平面 Euclidean plane中的其他简单形状图,即使图本身可能具有多达[math]\displaystyle{ O(n^2) }[/math]个边缘,也可以测试其是否而二分图,并在时间[math]\displaystyle{ O(n\log n) }[/math]中返回双色(判定为二分图)或奇数环(判定为非二分图)。[23]
奇环横贯
奇环横贯是一个 NP完全算法问题 NP-complete algorithmic problem(因不能用多项式算法而使问题无法解决的),在给定图形[math]\displaystyle{ G =(V,E) }[/math]和数字[math]\displaystyle{ k }[/math]的情况下,询问是否存在一组[math]\displaystyle{ k }[/math]个顶点,将其从[math]\displaystyle{ G }[/math]移除会导致生成为二分图。[24]这个问题是 固定参数可解 Fixed-parameter tractable的,这意味着存在一种算法,其运行时间可以由图形大小的多项式函数乘以增大系数[math]\displaystyle{ k }[/math]来确定。奇环横贯的名称源于:当且仅当图没有奇数环时,该图是二分图。因此,为了从图中删除顶点来获得二分图,就需要“命中所有奇数环”或找到所谓的奇环横贯集合。例如在图示中,图中的每个奇数环都包含蓝色(最底部)顶点,因此删除这些顶点就相当于删除了所有奇数环并留下一个二分图。
边二分化问题 Edge bipartization problem是删除尽可能少的边以使其成为二分图的问题,也是图修改算法中的重要问题。此问题同样是固定参数可解的,可以在时间[math]\displaystyle{ O\left(2^k m^2\right) }[/math],内解决,[25]其中k是要删除的边数,m是输入图中的边数。
匹配
一个图中的匹配是其边集的一个子集,其中任意两个边均不共享一个端点。 多项式时间算法 Polynomial time algorithms素以解决很多关于匹配的算法问题而得名,包括 最大匹配 Maximum matching(查找使用尽可能多的边的匹配), 最大权重匹配 Maximum weight matching和 稳定婚姻问题 Stable marriage。[26]在许多情况下,与非二分图相比,二分图上的匹配问题更容易解决,并且许多匹配算法(例如用于最大基数匹配的 Hopcroft-Karp算法)[27] 仅在二分图输入的时候才能正确运行。
举一个简单的例子,假设一组[math]\displaystyle{ P }[/math]的所有人都在一组[math]\displaystyle{ J }[/math]的职位中寻找工作,但并不是所有人都适合所有职位。可以将这种情况建模为一个二分图[math]\displaystyle{ (P,J,E) }[/math],其中当每个求职者找到其合适的工作时产生的关系就作为连边。[28]一个完美的匹配描述的是所有求职者同时找到所有工作的情况; 霍尔的婚姻定理 Hall's marriage theorem阐述的就是二分图允许完美匹配的特征。美国国民住院医师匹配项目采用的就是图形匹配法来解决美国医学生求职者和医院实习工作的匹配问题。
Dulmage–Mendelsohn 分解是二分图的结构分解,可用于寻找最大匹配。[29]
其他应用
二分图广泛应用于现代编码理论中,尤其是在对从通道接收到的密码进行解码领域。例如因子图 Factor graphs和 坦纳图 Tanner graphs。Tanner图是二分图,其中二分的一侧顶点表示一个密码数字,另一侧顶点表示一个数字的组合,这些数字的总和期望为零且不存在误差。因子图与置信网络密切相关,可用于LDPC和Turbo码的概率解码。
在计算机科学中,Petri网是用于分析和模拟并发系统的数学建模工具。该系统被建模为具有两组点集的二分有向图:一组“库所”点集用于容纳资源,以及一组“事件”点集用于生成和(或)消耗资源。他们通过约束节点和连边的传递来进一步限制系统的行为。Petri网利用二分有向图的属性和其他属性来允许对系统行为进行数学证明,同时还可以轻松实现系统仿真。
在射影几何中,Levi图是二分图的一种形式,可用于对配置点和线之间的入射进行建模。结合点和线的几何特性,即每两条线最多相交于一个点,并且每两个点都由一条线连接,因此Levi图不一定包含任何长度为4的环,进而其周长必须为6或更大。
另见
- 二分维度 Bipartite dimension,联合给定图的完全二分图最小量
- 二分双重覆盖 Bipartite double cover,一种通过双重复制顶点使原图形成两个不相交的副本从而将任意图转变为二分图的方法。
- 二分超图 Bipartite hypergraph,具有普遍二分性质的超图
- 二部拟阵 Bipartite matroid,包括二分图的图形拟阵,属于拟阵的一类。
- 二分图投影 Bipartite network projection,一种用于压缩有关双向网络信息的加权技术
- 凸双枝图 Convex bipartite graph,二分图的一种,其顶点可以排序使得相邻顶点是连续的
- 多重图 Multipartite graph,将二分图延伸到两个以上的顶点子集。
- 奇偶性图 Parity graph,具有二分图特性,同时同一点之间的每两个诱导路径具有相同的奇偶性
- 准二分图 Quasi-bipartite graph,一种斯坦纳树形Steiner tree问题实例,其中的终端形成一个独立的集合,从而允许近似算法将二分图的规范化
- 分割图 Split graph,图中顶点可以分为两个子集,其中一个子集是独立的,另一个成为团。
- Zarankiewicz 问题,关于禁止子图二分图的最大边数问题。
参考文献
- ↑ Diestel, Reinard (2005), Graph Theory, Graduate Texts in Mathematics, Springer, ISBN 978-3-642-14278-9
- ↑ Asratian, Armen S.; Denley, Tristan M. J.; Häggkvist, Roland (1998), Bipartite Graphs and their Applications, Cambridge Tracts in Mathematics, 131, Cambridge University Press, ISBN 9780521593458.
- ↑ 3.0 3.1 3.2 Asratian, Armen S.; Denley, Tristan M. J.; Häggkvist, Roland (1998), Bipartite Graphs and their Applications, Cambridge Tracts in Mathematics, 131, Cambridge University Press, ISBN 9780521593458
- ↑ Scheinerman, Edward R. (2012), Mathematics: A Discrete Introduction (3rd ed.), Cengage Learning, p. 363, ISBN 9780840049421.
- ↑ Chartrand, Gary; Zhang, Ping (2008), Chromatic Graph Theory, Discrete Mathematics And Its Applications, vol. 53, CRC Press, p. 223, ISBN 9781584888000
{{citation}}: Cite has empty unknown parameter:|1=(help). - ↑ Wasserman, Stanley; Faust, Katherine (1994), Social Network Analysis: Methods and Applications, Structural Analysis in the Social Sciences, vol. 8, Cambridge University Press, pp. 299–302, ISBN 9780521387071.
- ↑ Niedermeier, Rolf (2006), Invitation to Fixed Parameter Algorithms, Oxford Lecture Series in Mathematics and Its Applications, Oxford University Press, pp. 20–21, ISBN 978-0-19-856607-6
- ↑ Bracey, Robert (2012). "On the Graphical Interpreation of Herod's Coinage in Judaea and Rome in Coins". pp. 65–84.
- ↑ Archdeacon, D.; Debowsky, M.; Dinitz, J.; Gavlas, H. (2004), "Cycle systems in the complete bipartite graph minus a one-factor", Discrete Mathematics, 284 (1–3): 37–43, doi:10.1016/j.disc.2003.11.021.
- ↑ Ovchinnikov, Sergei (2011), Graphs and Cubes, Universitext, Springer. See especially Chapter 5, "Partial Cubes", pp. 127–181.
- ↑ Asratian, Armen S.; Denley, Tristan M. J.; Häggkvist, Roland (1998), Bipartite Graphs and their Applications, Cambridge Tracts in Mathematics, 131, Cambridge University Press, ISBN 9780521593458
- ↑ Biggs, Norman (1994), Algebraic Graph Theory, Cambridge Mathematical Library (2nd ed.), Cambridge University Press, p. 53, ISBN 9780521458979.
- ↑ Kőnig, Dénes (1931), "Gráfok és mátrixok", Matematikai és Fizikai Lapok, 38: 116–119.
- ↑ Gross, Jonathan L.; Yellen, Jay (2005), Graph Theory and Its Applications, Discrete Mathematics And Its Applications (2nd ed.), CRC Press, p. 568, ISBN 9781584885054.
- ↑ Chartrand, Gary; Zhang, Ping (2012), A First Course in Graph Theory, Courier Dover Publications, pp. 189–190, ISBN 9780486483689.
- ↑ Béla Bollobás (1998), Modern Graph Theory, Graduate Texts in Mathematics, vol. 184, Springer, p. 165, ISBN 9780387984889.
- ↑ Chudnovsky, Maria; Robertson, Neil; Seymour, Paul; Thomas, Robin (2006), "The strong perfect graph theorem", Annals of Mathematics, 164 (1): 51–229, arXiv:math/0212070, CiteSeerX 10.1.1.111.7265, doi:10.4007/annals.2006.164.51.
- ↑ Asratian, Armen S.; Denley, Tristan M. J.; Häggkvist, Roland (1998), Bipartite Graphs and their Applications, Cambridge Tracts in Mathematics, 131, Cambridge University Press, ISBN 9780521593458, p. 17.
- ↑ A. A. Sapozhenko (2001) [1994], "Hypergraph", Encyclopedia of Mathematics, EMS Press
- ↑ Brualdi, Richard A.; Harary, Frank; Miller, Zevi (1980), "Bigraphs versus digraphs via matrices", Journal of Graph Theory, 4 (1): 51–73, doi:10.1002/jgt.3190040107, MR 0558453. Brualdi et al. credit the idea for this equivalence to Dulmage, A. L.; Mendelsohn, N. S. (1958), "Coverings of bipartite graphs", Canadian Journal of Mathematics, 10: 517–534, doi:10.4153/CJM-1958-052-0, MR 0097069.
- ↑ Sedgewick, Robert (2004), Algorithms in Java, Part 5: Graph Algorithms (3rd ed.), Addison Wesley, pp. 109–111.
- ↑ Kleinberg, Jon; Tardos, Éva (2006), Algorithm Design, Addison Wesley, pp. 94–97.
- ↑ Eppstein, David (2009), "Testing bipartiteness of geometric intersection graphs", ACM Transactions on Algorithms, 5 (2): Art. 15, arXiv:cs.CG/0307023, doi:10.1145/1497290.1497291, MR 2561751.
- ↑ Yannakakis, Mihalis (1978), "Node-and edge-deletion NP-complete problems", Proceedings of the 10th ACM Symposium on Theory of Computing (STOC '78), pp. 253–264, doi:10.1145/800133.804355
- ↑ Guo, Jiong; Gramm, Jens; Hüffner, Falk; Niedermeier, Rolf; Wernicke, Sebastian (2006), "Compression-based fixed-parameter algorithms for feedback vertex set and edge bipartization", Journal of Computer and System Sciences, 72 (8): 1386–1396, doi:10.1016/j.jcss.2006.02.001
- ↑ Ahuja, Ravindra K.; Magnanti, Thomas L.; Orlin, James B. (1993), "12. Assignments and Matchings", Network Flows: Theory, Algorithms, and Applications, Prentice Hall, pp. 461–509.
- ↑ Hopcroft, John E.; Karp, Richard M. (1973), "An n5/2 algorithm for maximum matchings in bipartite graphs", SIAM Journal on Computing, 2 (4): 225–231, doi:10.1137/0202019.
- ↑ Ahuja, Ravindra K.; Magnanti, Thomas L.; Orlin, James B. (1993), "12. Assignments and Matchings", Network Flows: Theory, Algorithms, and Applications, Prentice Hall, pp. 463–464.
- ↑ Dulmage, A. L.; Mendelsohn, N. S. (1958), "Coverings of bipartite graphs", Canadian Journal of Mathematics, 10: 517–534, doi:10.4153/CJM-1958-052-0, MR 0097069
相关链接
编辑推荐
集智课程
二分图神经网络(BGNN)与推荐系统
本课程来自集智学园图网络论文解读系列活动。本课程是对论文《Bipartite Graph Neural Networks for Efficient Node Representation Learning》的解读。
图网络算法目前主要用于同质化的图。这篇论文结合图网络算法和二分图的特点提出了BGNN算法,适用于二分图上的学习。 该算法主要包括跨节点域的消息传递机制(inter-domain message passing)和同节点域的信息对齐(intra-domain alignment)机制. 通过采用GAN技术实现了无监督学习,又采用逐层训练的方法提升了算法效率,并在人工数据集和实际数据集上进行 试验,结果超越了现有的图表示学习方法。这些优势使BGNN有潜力应用于大规模推荐系统。
书籍领读:图论
本课程中,将讲解巴拉巴西网络科学书籍第一章图论。
漫谈图论的起源、发展与应用
本课程中,介绍了图论中的基本概念和网络科学使用的工具,可以帮助认识真实网络的关键性质。
本中文词条由Jie翻译,由CecileLi审校,薄荷编辑,如有问题,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。