信息生产：决策树

Again and again, the impossible problem is solved when we see that the problem is only a tough decision waiting to be made.一次又一次，当问题只是在于等待做出一个艰难的决定时，这个不可能解决的问题就已经被解决了。 ——Robert H. Schuller

Again and again, the impossible problem is solved when we see that the problem is only a chain of gradually simplified decisions waiting to be made. 一次又一次，当将问题简化为一个一个的小问题去解决时，这个不可能解决的问题就已经被解决了。 ——Xudong Cao

图1

 --趣木木（讨论）注：为利于审校和编辑后期工作的进行，遇到文本格式与页面格式显示差异较大的 会出现两次。含有参考文献的段落利于后期编辑，为第一个段落；不含格式的段落利于后期审校，为第二个段落。若段落不含参考文献 则仅以一段显示。下为实例：

含有参考文献 英文出现两次: A decision tree consists of three types of nodes:

A decision tree consists of three types of nodes:[1]

决策树包括以下三中类型的节点

不含参考文献 且内链不多 英文出现一次： A decision tree is a flowchart-like structure in which each internal node represents a "test" on an attribute (e.g. whether a coin flip comes up heads or tails), each branch represents the outcome of the test, and each leaf node represents a class label (decision taken after computing all attributes). The paths from root to leaf represent classification rules. 决策树是一种流程图式结构,其中每个内部节点表示对于一个属性上的“测试”(例如一个抛硬币是否出现正面或反面),每个分支代表测试的结果,每个叶节点代表一种类别(在计算所有特征/属性后进行决策)。从根到叶的路径表示分类规则。

引言

如果突然问你"有一个陌生人叫甲,他（她）今天需要带伞吗?", 你一定会觉得这个问题就像问你"两千米外有一个超市,问超市里面有多少卷卫生纸"一样突兀。可能几秒钟之后你会说"这要依情况而定, 如果今天烈日炎炎并且甲是一个皮肤白皙的中国姑娘,或者外面下着大雨并且甲是一个不得不去步行上班的屌丝码农, 那么他（她）今天需要带伞, 否则不要。"

当谈及这个看似无聊的问题的时候我们在谈什么？ 恩，在谈方法。我们经常会遇到简单但又困难的抉择。说抉择简单是因为候选方案简单而且清晰。例如,要不要出国留学,要不要辞职创业,要不要投资黄金等等。但是这些看似简单的选项背后却是困难的抉择。 面对这些困难的抉择，一开始，很可能不知所措。 值得庆幸的是, 很多时候, 这些看似不可能解决的问题, 最终可以被化解成一连串越来越简单的问题, 然后解决掉。这个方法可以粗俗总结为: "如果这样这样这样, 那么选择A; 如果那样那样那样, 那么选择B", 当然这种方法有一个更加简洁形象的名字--决策树 Decision Tree , 也就是该词条的主题。

决策树 Decision Tree 是在已知各种情况发生概率的基础上，通过构成决策树来求取净现值的期望值大于等于零的概率，评价项目风险，判断其可行性的决策分析方法，是直观运用概率分析的一种图解法。

A decision tree is a decision support tool that uses a tree-like model of decisions and their possible consequences, including chance event outcomes, resource costs, and utility. It is one way to display an algorithm that only contains conditional control statements.

A decision tree is a decision support tool that uses a tree-like model of decisions and their possible consequences, including chance event outcomes, resource costs, and utility. It is one way to display an algorithm that only contains conditional control statements. 它是只包含条件控制语句（if,else等）的一种算法。决策树利用类似于树的决策模型及其可能的结果（包括机会事件的结果、资源成本和效用）作为工具来支持决策。由于其决策分支画成图形很像一棵树的枝干，故称决策树。

Decision trees are commonly used in operations research, specifically in decision analysis, to help identify a strategy most likely to reach a goal, but are also a popular tool in machine learning. Decision trees are commonly used in operations research, specifically in decision analysis, to help identify a strategy most likely to reach a goal, but are also a popular tool in machine learning. 决策树通常用于运筹学研究，特别是在决策分析中，去帮助识别最有可能实现目标的策略，但同样也在机器学习中比较常用。在机器学习中，决策树是一个预测模型，他代表的是对象属性与对象值之间的一种映射关系，是监督学习中的一种。

 --趣木木（讨论）加以补充 "他代表的是对象属性与对象值之间的一种映射关系，是监督学习中的一种。"

概览

A decision tree is a flowchart-like structure in which each internal node represents a "test" on an attribute (e.g. whether a coin flip comes up heads or tails), each branch represents the outcome of the test, and each leaf node represents a class label (decision taken after computing all attributes). The paths from root to leaf represent classification rules. 决策树是一种流程图式结构,其中每个内部节点表示对于一个属性上的“测试”(例如一个抛硬币是否出现正面或反面),每个分支代表测试的结果,每个叶节点代表一种类别(在计算所有特征/属性后进行决策)。从根到叶的路径表示分类规则。

In decision analysis, a decision tree and the closely related influence diagram are used as a visual and analytical decision support tool, where the expected values (or expected utility) of competing alternatives are calculated. 在决策分析 Decision Analysis中，决策树与影响图紧密相关，它们是可视化且具有分析性的决策支持工具，可用来计算在竞争方案中的期望值 Expected Value和期望效用 Expected Utility。

其中，影响图是由结点和有向弧组成的无环路的有向图。结点代表所研究问题中的主要变量，有向弧表示变量间的各种相互关系。它是根据决策者（或委托人）对问题的描述，结合专家的知识表示问题结构的一种直观图形，在图中明确地揭示出变量间的关系，尤其是变量间的条件独立和信息流向。影响图作为处理不确定性问题的工具可广泛地应用于决策分析、不确定性建模和人工智能的各个领域。

Much of the information in a decision tree can be represented more compactly as an influence diagram, focusing attention on the issues and relationships between events. 决策树中的许多信息可以更简洁地表示为影响图，更加关注问题和事件之间的关系。

  --趣木木（讨论）加以补充了影响图的一些概念

A decision tree consists of three types of nodes:

A decision tree consists of three types of nodes:[1]

决策树包括以下三中类型的节点

1. Decision nodes – typically represented by squares
2. Chance nodes – typically represented by circles
3. End nodes – typically represented by triangles

• □—-决策点-用正方形来表示。是对几种可能方案的选择，即最后选择的最佳方案。如果决策属于多级决策，则决策树的中间可以有多个决策点，以决策树根部的决策点为最终决策方案。
• ○——状态节点-用圆圈表示。代表备选方案的经济效果（期望值），通过各状态节点的经济效果的对比，按照一定的决策标准就可以选出最佳方案。由状态节点引出的分支称为概率枝，概率枝的数目表示可能出现的自然状态数目每个分枝上要注明该状态出现的概率。
• △——结果节点-用三角形表示。将每个方案在各种自然状态下取得的损益值标注于结果节点的右端。

 --趣木木（讨论）分别对决策点 状态节点 结果节点进行了补充

Decision trees are commonly used in operations research and operations management. If, in practice, decisions have to be taken online with no recall under incomplete knowledge, a decision tree should be paralleled by a probability model as a best choice model or online selection model algorithm. Another use of decision trees is as a descriptive means for calculating conditional probabilities. Decision trees are commonly used in operations research and operations management. If, in practice, decisions have to be taken online with no recall under incomplete knowledge, a decision tree should be paralleled by a probability model as a best choice model or online selection model algorithm. Another use of decision trees is as a descriptive means for calculating conditional probabilities. 决策树常用于运筹学和运营管理领域。在实践中，如果决策是在信息有缺失且不需回忆的情况下进行时，那么决策树应该与概率模型一样，是最优选择模型/在线选择模型算法。决策树也是一种计算条件概率的描述性方法。

 --趣木木（讨论）online selection model algorithm 只查到有在线学习算法  会再查询一下 

Decision trees, influence diagrams, utility functions, and other decision analysis tools and methods are taught to undergraduate students in schools of business, health economics, and public health, and are examples of operations research or management science methods. 决策树、影响图、效用函数以及其他决策分析工具和方法常作为商学院、卫生经济学和公共卫生学院的本科生教学内容。它们也是运筹学或管理科学方法的一些示例。

定义

决策树是一种分而治之 Divide and Conquer 的决策过程。一个困难的预测问题, 通过树的分支节点, 被划分成两个或多个较为简单的子集，从结构上划分为不同的子问题。将依规则分割数据集的过程不断递归下去 。随着树的深度不断增加，分支节点的子集越来越小，所需要提的问题数也逐渐简化。当分支节点的深度或者问题的简单程度满足一定的停止规则 Stopping Rule 时, 该分支节点会停止劈分，此为自上而下的停止阈值 Cutoff Threshold 法；有些决策树也使用自下而上的剪枝 Pruning 法。

历史

决策树含义直观,容易解释。对于实际应用,决策树还有其他算法难以比肩的速度优势。这使得决策树，一方面能够有效地进行大规模数据的处理和学习；另一方面在测试/预测阶段满足实时或者更高的速度要求。历史上,因为预测结果方差大而且容易过拟合，决策树曾经一度被学术界冷落。但是在近十年, 随着集成学习 Ensemble Learning 的发展和大数据时代的到来，决策树的缺点被逐渐克服， 同时它的优点得到了更好的发挥。在工业界, 决策树以及对应的集成学习算法(如Boosting,随机森林)已经成为解决实际问题的重要工具之一。 其成功应用在人脸检测,人体动作识别 Body Tracking 。

组成部分

文件:Manual decision tree.jpg

图3 Traditionally, decision trees have been created manually.图3 传统上，决策树是手动创建的

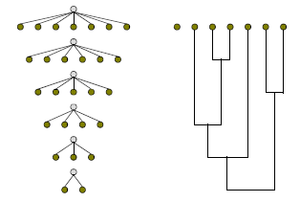
Drawn from left to right, a decision tree has only burst nodes (splitting paths) but no sink nodes (converging paths). Therefore, used manually, they can grow very big and are then often hard to draw fully by hand. Traditionally, decision trees have been created manually – as the aside example shows – although increasingly, specialized software is employed. 从左到右绘制的决策树只有分支节点(具有分裂路径)，没有汇聚节点(具有聚合路径)。因此，如果利用手工绘制，它们会变得非常大，且通常很难完全完成。传统上，决策树是手工创建的。正如图3所示——尽管越来越多地使用专门的软件。

分支节点

按照分支节点的字面意思, 其决定输入数据进入哪一个分支。每个分支节点对应一个分支函数(劈分函数)，将不同的预测变量的值域映射到有限、离散的分支上。

根节点

根节点是一个特殊的分支节点，它是决策树的起点。

对于决策树来说，所有节点的分类或者回归目标都要在根节点已经定义好了。如果决策树的目标变量是离散的（序数型或者是列名型变量），则称它为分类树 Classification Tree ；如果目标变量是连续的（区间型变量），则称它为回归树 Regression Tree 。

叶节点

叶节点存储了决策树的输出。对于分类问题，所有类别的后验概率都存储在叶节点，观测走过了全树从上到下的某一条路径（决策过程）之后会根据叶子节点给出一个“观测属于哪一类”的预报；对于回归问题，叶子结点上存储了训练集目标变量的中位数，不同观测走过决策路径后如果到达了相同的叶子结点，则对它们给出相同预报。

训练

一棵决策树由分支节点(树的结构)和叶节点(树的输出)组成。决策树训练的目标是通过最小化某种形式的损失函数或者经验风险来确定每个分支函数的参数,以及叶节点的输出。

决策树自上而下的循环分支学习 Recursive Regression 采用了贪心算法。每个分支节点只关心自己的目标函数。具体来说, 给定一个分支节点, 以及落在该节点上对应样本的观测（包含自变量与目标变量），选择某个（一次选择一个变量的方法很常见）或某些预测变量，也许会经过一步对变量的离散化（对于连续自变量[math]\displaystyle{ X }[/math]而言），经过搜索不同形式的分叉函数且得到一个最优解（最优的含义是特定准则下收益最高或损失最小）。这个分支过程, 从根节点开始, 递归进行, 不断产生新的分支, 直到满足结束准则时停止。整个过程和树的分支生长非常相似。

决策规则

The decision tree can be linearized into decision rules, where the outcome is the contents of the leaf node, and the conditions along the path form a conjunction in the if clause. In general, the rules have the form: The decision tree can be linearized into decision rules,[2] where the outcome is the contents of the leaf node, and the conditions along the path form a conjunction in the if clause. In general, the rules have the form: 决策树能够将决策规则线性化，其中叶节点的内容是结果，在if语句中的连接所产生的路径是条件。一般来说，规则的形式如下:

if condition1 and condition2 and condition3 then outcome.

如果“条件1”和“条件2”和“条件3”，则“结果”

Decision rules can be generated by constructing association rules with the target variable on the right. They can also denote temporal or causal relations. Decision rules can be generated by constructing association rules with the target variable on the right. They can also denote temporal or causal relations.[3] 可以通过利用右侧的目标变量来构造关联、生成决策规则。它们也可以表示时间或因果关系。

使用流程图符号的决策树Decision tree using flowchart symbols

Commonly a decision tree is drawn using flowchart symbols as it is easier for many to read and understand. 通常，决策树是使用流程图符号来绘制的，因为这样更容易阅读和理解。

文件:DecisionCalcs.jpg

图4

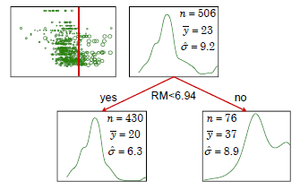
测试(预测)

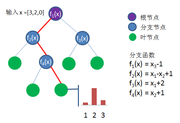
图5提供了一个简单的例子说明决策树的测试过程。测试样本为 [math]\displaystyle{ x = [3,2,0]; }[/math]

1. 进入根节点, 分支函数 [math]\displaystyle{ f_1(x) = x_3 - 1 = 0 - 1 = -1 }[/math] 小于0， 进入左分支
2. 分支函数 [math]\displaystyle{ f_2(x) = x_1 - x_2 + 1 = 3 - 2 + 1 = 2 }[/math] 大于0, 进入右分支
3. 分支函数 [math]\displaystyle{ f_4(x) = x_2 + 1 = 2 + 1 = 3 }[/math] 大于0, 进入右分支, 已经到达叶节点
4. 假设是三分类问题, 该叶节点上所有类别的后验概率是 (0.1, 0.7, 0.2), 那么该决策树预测输入样本属于第二类.

图5

分支节点(树的结构)

如前文所述, 决策树训练的核心是学习分支节点上的分支函数。

分支函数形式

在具体的学习过程中， 需要明确定义分支函数的具体形式. 常用的函数的形式都非常的简单如:

• 一维线性函数: [math]\displaystyle{ f(x) = x_i + b }[/math]
• 多维线性函数: [math]\displaystyle{ f(x) = \lt a,x\gt + b }[/math], 其中[math]\displaystyle{ \lt a,x\gt }[/math]表示向量内积。

一般地，在常见的工程应用中使用一维线性函数。计算允许的条件下使用2-3个变量的线性组合作为分支函数的可能形式。

分支函数选择

为寻找合适的决策变量[math]\displaystyle{ X }[/math]与分支函数[math]\displaystyle{ f(x:X\rightarrow B) }[/math]，首先要找到全部的把[math]\displaystyle{ X }[/math]变量的不同水平集合[math]\displaystyle{ L }[/math]映射到预先设置好的节点分叉集 Branches [math]\displaystyle{ B }[/math]上的解集，得到[math]\displaystyle{ \{g(L \rightarrow B)\} }[/math]。[math]\displaystyle{ X }[/math]到[math]\displaystyle{ L }[/math]上的映射[math]\displaystyle{ h(X \rightarrow L) }[/math]，对于离散型变量而言就是对自身的映射，而对于连续型变量而言是向所属离散化区段的映射。最后得到分支函数的备选集合[math]\displaystyle{ \{f(x:X \rightarrow B)\} = \{g(h(x))\} }[/math]。

图6

如图6，我们可以看到对于任意区间型或者序数型的变量X与任意单调映射f，使用X和f(X)作为预测函数的变量，决策树的结果没有改变。同理，单独变化极端值也不会对决策树结果进行影响。可以说这种分支函数的选择使得决策树建模具有稳健性。

建立用于分支函数选择的函数集合

• 设定决策树为[math]\displaystyle{ B }[/math]叉树，预测变量[math]\displaystyle{ X }[/math]（即分支函数的自变量）属于有[math]\displaystyle{ L }[/math]个水平的序数型(Ordinal)变量，或者[math]\displaystyle{ X }[/math]为被离散化成[math]\displaystyle{ L }[/math]段的区间型(Interval)变量。

注：后一种情况不仅把问题等价于处理[math]\displaystyle{ L }[/math]个不同水平的序数型变量，而且有效避免了极端值的影响。

举例以说明：

[math]\displaystyle{ f(x)=x-a \begin{cases} \lt =0 &\text{then go to the left branch}\\ \gt 0 &\text{then go to the right branch} \end{cases} }[/math]

[math]\displaystyle{ f(X) }[/math]为决定一个含X观测的样本进入左分支还是右分支的判断条件。此函数即为一个合理的备选分支函数。

更一般地，选择函数[math]\displaystyle{ g(L\rightarrow B) }[/math]时，映射[math]\displaystyle{ \{1,2,3,4\} \rightarrow \{1,1,2,2\} }[/math]，[math]\displaystyle{ \{1,2,3,4\} \rightarrow \{1,1,1,2\} }[/math]是被允许的，而[math]\displaystyle{ \{1,2,3,4\} \rightarrow \{1,2,2,1\} }[/math]是不被允许的，因为各个分叉之间没有办法继续保持排序性了。

在处理[math]\displaystyle{ L }[/math]个水平的序数型变量时，可以得到[math]\displaystyle{ L-1 }[/math]可选的截断点，从中挑选[math]\displaystyle{ B-1 }[/math]个位置截断，以保持排序性。

因此，进行最多[math]\displaystyle{ B }[/math]分叉时，搜索可得到备选分支函数的总数为一组组合数的和：

[math]\displaystyle{ \sum_{b=2}^{B} C_{L-1}^{b-1} }[/math]

易得，在二叉树时，需要搜索的备择分支函数总数仅有[math]\displaystyle{ L-1 }[/math]个。

• 设定决策树为[math]\displaystyle{ B }[/math]叉树，预测变量[math]\displaystyle{ X }[/math]属于有[math]\displaystyle{ L }[/math]个水平的列名型(Nominal)变量，则水平之间是无序的。

举例以说明：

X是列名型变量，取值为[math]\displaystyle{ \{1,2,...,9\} }[/math]，水平之间不存在排序关系。若函数形式为

[math]\displaystyle{ f(x) = x%3 }[/math]

一个观测点依据变量X的取值除以3的余数来选择究竟要进入0，1，2分支中的哪一个。因为原变量是无序的，分支也自然无法定义有序，此函数为一个合理的分支函数。

在处理[math]\displaystyle{ L }[/math]个水平的序数型变量时，不考虑水平之间的顺序与分叉之间的顺序，将他们分进不同的[math]\displaystyle{ B }[/math]个分叉上，其总数为第二类斯特林数[math]\displaystyle{ S(L,B) }[/math](Stirling Number of the second kind)。

求解第二类斯特林数的边界条件表达式/迭代式分别为：[math]\displaystyle{ S(L,1)=1; S(L,B)=B\cdot{S}(L-1,B)+S(L-1,B-1) }[/math]

第二类斯特林数表：

L\B	2	3	4	...	总
2	1			...	1
3	3	1		...	4
4	7	6	1	...	14
5	15	25	10	...	51
6	31	90	65	...	202
7	63	301	350	...	876
8	127	966	1701	...	4139

考虑所有[math]\displaystyle{ B }[/math]的可能（从2到[math]\displaystyle{ L }[/math]）并求和，称为贝尔数 Bell Number：

[math]\displaystyle{ B_L=\sum_{b=1}^L{S(L,b)} }[/math]

在实际问题中，为避免备择函数总数增加过快，我们也会限制分叉数最大值[math]\displaystyle{ B_{max} }[/math]不超过5，常选择2或3；这样也避免了搜索贝尔数[math]\displaystyle{ \sum_{b=2}^L{S(L,b)}=B_L - 1 }[/math] 这样多的备择分支函数，将搜索数缩小到了[math]\displaystyle{ \sum_{b=2}^{B_{max}}{S(L,b)} }[/math]。

其他有助于优化搜索的方法：

• 用于搜索的变量在全树中只使用一次
• 节点内部采样，减少观测
• 对[math]\displaystyle{ L }[/math]个水平进行层次聚类。CHAID使用了这种技术：

图7

1. 处理序数型或区间型变量时，在层次聚类时只考虑相邻分支的聚类，选择条件是“两个分支在目标变量上的分布最接近”（卡方意义上）；

从[math]\displaystyle{ L }[/math]个水平作为从[math]\displaystyle{ L }[/math]个不同分支开始，每次聚类减少一个分支；

在已有[math]\displaystyle{ B' }[/math]个分支时，需要考虑的聚类选择一共有[math]\displaystyle{ (B'-1)/2 }[/math]种；

于是，依次比较了[math]\displaystyle{ L-1 }[/math]，[math]\displaystyle{ L-2 }[/math]，...，[math]\displaystyle{ 1 }[/math]个，一共[math]\displaystyle{ L(L-1)/2 }[/math]个备择模型，得到分支数分别为[math]\displaystyle{ L,L-1,....,1 }[/math]的各1个模型（共[math]\displaystyle{ L }[/math]个）从中选取最优；

1. 处理列名型变量时，在层次聚类时考虑任意两个分支的聚类；

从[math]\displaystyle{ L }[/math]个水平作为从[math]\displaystyle{ L }[/math]个不同分支开始，每次聚类减少一个分支；

在已有[math]\displaystyle{ B' }[/math]个分支时，需要考虑的聚类选择一共有[math]\displaystyle{ B'(B'-1)/2 }[/math]种；

于是，依次比较了[math]\displaystyle{ L(L-1)/2 }[/math]，[math]\displaystyle{ (L-1)(L-2)/2 }[/math]，...，[math]\displaystyle{ 1 }[/math]个，一共[math]\displaystyle{ (L+1)L(L-1)/6 }[/math]个备择模型，得到分支数分别为[math]\displaystyle{ L,L-1,....,1 }[/math]的各1个模型（共[math]\displaystyle{ L }[/math]个）从中选取最优。

选择最优分支函数

得到备选集合后，我们选取的最优分支函数应该使得其全部子节点上的样本的加权损失函数和最小。

• 假设当前分支节点所有样本为 [math]\displaystyle{ \{ x_1,x_2,...,x_n\} }[/math], 对应的类别标签为[math]\displaystyle{ \{ y_1,y_2,...,y_n\} }[/math]
• 分支函数[math]\displaystyle{ f(x: X \rightarrow B) }[/math]将样本划分到两个或多个子节点. 其中[math]\displaystyle{ \mathcal{X}_{b} = \{x_i | f(x_i)=b\} }[/math] 表示第[math]\displaystyle{ b }[/math]个子节点样本的集合，[math]\displaystyle{ b \in \{1,2,...,B\} }[/math]
• [math]\displaystyle{ \mathcal{Y}_{b}, b \in \{1,2,....,B\} }[/math] 为对应的标签集合.

使用以上定义的符号, 分支函数的学习准则可以描述成如下的优化问题:

[math]\displaystyle{ f^* = \underset{f}\text{argmin} ( \sum_{b=1}^{B} L(\mathcal{X}_{b}, \mathcal{Y}_{b}) ) }[/math]

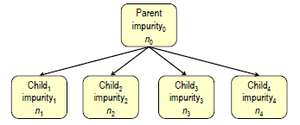
其中损失函数[math]\displaystyle{ L(\mathcal{X}, \mathcal{Y}) }[/math] 描述了样本的不纯度带来的损失。对于一个子节点[math]\displaystyle{ b }[/math]，给定样本数，如果其中样本的标签都相同, 那么样本纯度很高, 对应的损失函数值低；如果样本标签随机分布, 那么样本纯度很低，对应的损失函数值高。给定[math]\displaystyle{ \mathcal{Y} }[/math]在分类集上的概率密度，如果标签都相同，那么不管样本数的多少，纯度都很高，损失为0；如果标签随机分布，纯度很低，那么样本总数越多，带来的损失就越大。

损失函数形式设定

在实际训练中, 需要根据不同的需求选择适当的损失函数是必须的，损失函数的形式即是我们选择最优分支函数的优化目标。

分类树损失函数

假设[math]\displaystyle{ p_i }[/math]表示第[math]\displaystyle{ i }[/math]样本数量占所有样本总量[math]\displaystyle{ n }[/math]的百分比。

不同准则下，使用损失函数可以得到每次分支带来损失下降的规律：

图8

基尼不纯度 Gini impurity 准则

[math]\displaystyle{ l_{G}(p) \propto n \sum_{i=1}^{m} p_i (1-p_i) }[/math]

按其定义式所表达的，它的含义是“任意取两个观测其属于不同类的概率”。生态学中，与Simpson's Diversity Index具有相同定义。

图9

在分支时的基尼不纯度改进为：

[math]\displaystyle{ \Delta Gini = i(0)-(\frac{n_1}{n_0}i(1)+\frac{n_2}{n_0}i(2)+\frac{n_3}{n_0}i(3)+... ) }[/math]，[math]\displaystyle{ \{n_0,n_1,n_2,n_3,...\} }[/math]分别为当前节点与其分支节点的观测数；

基尼不纯度改进越大，说明分支后各个子节点任取两个观测数与不同类的概率越低；

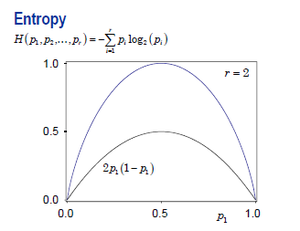
信息熵(Information entropy)准则

[math]\displaystyle{ l_{E}(p) \propto - n \sum^{m}_{i=1} p_i \log^{}_2 p_i }[/math]

按其定义式所表达的，它的含义是“在该节点内使用变长码字对类别进行编码，所能达到的最优平均码字长度”

图10

在分支时的调减熵减为：

[math]\displaystyle{ \Delta H = H(0)-(\frac{n_1}{n_0}H(1)+\frac{n_2}{n_0}H(2)+\frac{n_3}{n_0}H(3)+... ) }[/math]

熵减越大，说明节点经过一步分支后，各节点都能以较短的变长码字进行编码；

对数价值 Logworth 准则

在分支时，分支规则与对目标规则关联性越强，皮尔逊卡方检验值 Pearson's Chi-Square Test 对应P值的负对数 [math]\displaystyle{ -log_{10}(P(\mathcal{X}_{\nu}^2\gt \sum_{i,j}\frac{(O_{ij}-E{ij})^2}{E_{ij}})) }[/math]就越大。

其中，皮尔逊卡方统计量为在0假设（分支对分类毫无改进）下所有加权误差平方之和[math]\displaystyle{ \sum_{i,j}\frac{(O_{ij}-E{ij})^2}{E_{ij}} }[/math]，其中自由度[math]\displaystyle{ \nu=(B-1)(card(Y)-1) }[/math]

经过Kass调整（Bonferroni界调整）的对数价值 P-Adjusted Logworth 准则

[math]\displaystyle{ -log_{10}(mP) = \mbox{Logworth} -log_{10}{m} }[/math]

直觉上我们对对数价值法进行反思考虑如下的问题：如果我们尝试足够多的分支大小与可能性，是否我们在滥用Logworth法？我们把备择分支方案数目增大100倍，自然会选到Logworth函数更大的分支函数，而一味的细分分支使用的变量[math]\displaystyle{ X }[/math]丝毫不能说明[math]\displaystyle{ X }[/math]的预测强度正在变强。

我们将Logworth进行调整，减掉的部分为[math]\displaystyle{ -log_{10}(m) }[/math]，其中[math]\displaystyle{ m }[/math]即为前面推导的“[math]\displaystyle{ L }[/math]水平，[math]\displaystyle{ B }[/math]分支时，全部备择分支函数集合”的大小：

  ---趣木木（讨论）Logworth释义未查询到合适结果

[math]\displaystyle{ m=\left\{\begin{array}{ll} C_{L-1}^{B-1} \mbox{ , when X is Ordinal/Interval} & \\ S(L,B) \mbox{ , when X is Nominal} & \end{array}\right. }[/math]

Y\B	X Total	X<5	X>=5	E(X<5)	E(X>=5)	(O-E)^2/E (X<5)	(O-E)^2/E (X>=5)
1	364	293	71	239	125	12	23
2	364	363	1	239	125	64	123
3	336	42	294	220	116	139	273

本例中：

[math]\displaystyle{ \Delta Gini=0.197, \Delta H=0.504, \mbox{Logworth}=140, m=96, \mbox{Adjusted Logworth}=138 }[/math]

回归树损失函数

方差的最大似然估计 MLE of Variance 准则

很自然的，对于回归树而言，某子节点[math]\displaystyle{ b }[/math]上的所谓“不纯度”可以用其因变量[math]\displaystyle{ Y }[/math]的方差来表示：

图9

[math]\displaystyle{ {Var}_b = \frac{1}{n_b}\sum_{j=1}^{n_b}(y_{jb}-\bar{y}_b)^2 }[/math]

绝对偏差 Least Absolute Deviation 准则

[math]\displaystyle{ {LAD}_b = \frac{1}{n_b}\sum_{j=1}^{n_b}|y_{jb}-\bar{y}_b| }[/math]

分支规则的F检验 Branching's F-Test 准则

根据传统的单路方差分析 One-Way Analysis of Variance ，可以得到如下定义：

分支节点间方差：[math]\displaystyle{ SS_{between}=\sum_{b=1}^B n_b(\bar{y}_b-\bar{y})^2 }[/math]

分支节点内方差：[math]\displaystyle{ SS_{within}=\sum_{b=1}^B\sum_{j=1}^{n_b} (\bar{y}_b-y_{jb})^2 }[/math]

分支前总方差：[math]\displaystyle{ SS_{between}=\sum_{b=1}^B\sum_{j=1}^{n_b} (\bar{y}-y_{jb})^2 }[/math]

F-统计量检验：

[math]\displaystyle{ F=(\frac{SS_{between}}{SS_{within}})(\frac{n-B}{B-1}) \sim F_{B-1,n-B} }[/math]

这些在强烈异方差性下表现并不稳定。建议先对因变量[math]\displaystyle{ Y }[/math]做合适的变换（如乘幂，取对数等）防止稳定性降低。

分支时的缺失值处理

在实际问题处理中，在合理的数据清洗后，如果发现分支变量[math]\displaystyle{ X }[/math]含有缺失值的观测点较多，可以把选择缺失值作为一个单独的水平来搜索最优分支函数；缺失值较少的情况下可以考虑先只考虑无缺失值的最优分支函数，再将缺失值并入最大的一个分支或者后验概率最接近的一个分支。

如果使用“缺失值用于分支搜索”的方案，缺失值的出现无法保证原有的序数型/区间型变量存在一个水平排序用于模型选择，所以：

• 处理序数型/区间型变量：无缺失值情况下如果发生了[math]\displaystyle{ b }[/math]个分支，只需要考虑缺失值作为独立分支或者附着于[math]\displaystyle{ b }[/math]个分支中的某一个的一共[math]\displaystyle{ b+1 }[/math]种情况；

• 处理列名型变量：简单地把缺失值作为独立水平进行搜索。

如果使用“缺失值用于推断”的方案，首先使用变量重要性来描述变量并排序，然后根据观测在某些变量是否为缺失值判断是否能由观测点得到可靠的预报。

在实际使用中，如果变量间有较强的局部/全局共线性，使用这种方法是不当的。

叶节点(树的输出)

• 对于分类树, 决策树的叶节点上的输出就是所有类别的后验概率 [math]\displaystyle{ P(c|x) }[/math]. 可以用该叶节点各类别样本的频率来近似后验概率 [math]\displaystyle{ P(c|x) }[/math]. 后验概率最大的类别就是决策树对于新进单个观测点的预测结果，也就是 [math]\displaystyle{ c^* = \underset{c}{\text{argmax}} P(c|x) }[/math]。
• 对于回归树，决策树的叶节点上的输出是叶子结点上观测点目标变量[math]\displaystyle{ Y }[/math]的中位数。

决策树停止生长准则

前向截止条件

• 最大深度： 树的节点的深度指的是，从根节点出发到当前节点的路径长度。如果某个节点的深度已经达到预先设定的深度，那么就停止分支, 该节点被设定为叶节点。
• 最少样本数量：一般来说，叶节点的样本量越多，推广力越强。反之, 则容易过拟合。限制叶节点的最低样本量有助于提升决策树的推广能力。 如果当前节点样本量已经低于预先设定的阈值，那么停止分支。
• 纯度准则：分支过程若导致节点上不断地降低基尼不纯度/熵/节点内方差等，说明纯度一直在改进。达到特定的纯度即可停止分支。

这样得到的模型称为最大树 Largest Tree 或者全树。

后向剪枝条件

图10

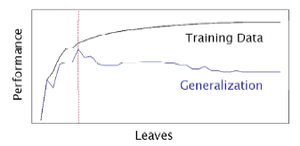
在训练集上正确率随着叶子节点的增加而增加，但模型在验证数据集上，叶子节点数超过某个阈值后泛化能力反而会减弱。有时我们要在正向分支过程上创造远多于我们所需要的节点（如使用层数停止准则），然后根据一定规则，使用验证数据集进行后向剪枝。

使用后向剪枝的根本原因是，分支准则的局部最优性很可能不会使某一层所有分支节点的提升都均匀，甚至差距很大。那些提升不够显著的节点要从前向截止得到的模型中删除，留下一个全树的子树作为最终模型。

有时为了优化泛化性能，我们不仅考虑子树，也考虑那些通过比某子树多一次分枝能得到的非子树，在验证集上比较效果。

• 最小化误分类/最大化准确度（分类树）：

[math]\displaystyle{ \mbox{Accuracy}=\frac{n_{TP}+n_{TN}}{n} }[/math]

• 最大化收益（分类树）：

我们可以做更宽泛的假设，对不同类的观测进行预测产生的误分类，导致的利润（损失）也是不一样的。 [math]\displaystyle{ \mbox{Profit}=\mbox{Profit}_{TP}\frac{n_{TP}}{n}+\mbox{Profit}_{TN}\frac{n_{TN}}{n}+\mbox{Profit}_{FP}\frac{n_{FP}}{n}+\mbox{Profit}_{FN}\frac{n_{FN}}{n} }[/math]

• 纯度准则（分类树，回归树）：

在前向剪枝中，可能设定了一个较为宽的纯度标准以使得树得以充分发展，而后在后向剪枝中保留其包含N个结点的纯度提升最大的子树。

• ASE 平均平方误差（分类树，回归树）：

使用平均平方误差作为后向剪枝准则是使用纯度准则的一个特例。对于回归树这一点不难理解，对于分类树来说，这是在验证集上重新计算类似基尼不纯度的指标：

[math]\displaystyle{ ASE = 1 - \sum_{i=1}^N p_{i-train}p_{i-valid} }[/math]

• 稳健性模型选择

根据前面定义的几种评价树的规则（损失或者收益函数），定义树模型的选择标准，最小化下式：

[math]\displaystyle{ R_{\alpha}(T)=R(T)+\alpha |T| }[/math]

其中T为树的总结点个数。这个定义有点像模型选择中的信息选择的定义（SBC, AIC等）：选择越多变量或者树的节点越多，解释性越强，训练集上的风险越小，但泛化性能也会变差。合理选择参数[math]\displaystyle{ \alpha }[/math]，使得损失与树的节点个数的某个线性叠加最小，这样模型会更稳健。

• 提升度方法（分类树）：

如果我们特定感兴趣某一类事件A，我们可以通过把A事件在每一个叶子结点中出现的比例从大到小排序。设其在整个观测中出现的比例为[math]\displaystyle{ P_A }[/math]

依次加入这些叶子结点，我们得到从0%到100%观测的序列，这中间预测正确的A事件的概率（预测性能）从一个很高的值[math]\displaystyle{ P^*_A }[/math]下降到[math]\displaystyle{ P_A }[/math]，这样考察前面尽量少的一部分比例的观测点可以提取出尽量多的A事件。这条轨道上的每一个值比上[math]\displaystyle{ P_A }[/math]得到了一条新的轨道，称为Lift曲线，在100%观测处轨道下降到1。一条值恒为1的水平线称为基准线 Baseline。

模型性能诊断

决策树本身是一种非常不稳定，容易产生过拟合的模型。使用分类问题常用的性能诊断方法对模型在训练集与测试集上进行比较。

对于分类树，经常使用的方法有提升图 Lift Chart，收益图 Gains Chart 等。

决策树与罗斯·昆兰

说起决策树学习,就必然要谈到澳大利亚计算机科学家罗斯·昆兰 J. Ross Quinlan (1943- )。最初的决策树算法是心理学家兼计算机科学家E. B.Hunt1962年在研究人类的概念学习过程时提出的CLS Concept Learning System。罗斯·昆兰在Hunt的指导下于1968年在美国华盛顿大学获得计算机博士学位,然后到悉尼大学任教。1978 年他在学术假时到斯坦福大学访问，选修了图灵的助手开设的一门研究生课程。课上有一个大作业，要求写程序来学习出完备正确的规则，以判断国际象棋残局中一方是否会在两步棋后被将死。昆兰写了一个类似于CLS的程序来完成作业,其中最重要的改进是引入了信息增益准则。（下有涉及）后来他把这个工作整理出来在1979年发表,这就是ID3算法。

 --趣木木（讨论）补充   E. B.Hunt未找到释义

1986年机器学习 Machine Learning杂志创刊，昆兰应邀在创刊号上重新发表了ID3算法,掀起了决策树研究的热潮。短短几年间众多决策树算法问世, ID4、ID5等名字迅速被其他研究者提出的算法占用，昆兰只好将自己的ID3后继算法命名为C4.0,在此基础上进一步提出了著名的C4.5。有趣的是,昆兰自称C4.5仅是对C4.0做了些小改进，因此将它命名为“第4.5代分类器”，而将后续的商业化版本称为C5.0。

成熟的决策树算法

在实践中，不同的分支函数与结束准则往往对于解决不同的问题有不同的效果，科学软件以及商业软件更倾向于将各种成熟的准则/参数配置/优化方案作为一个整体并命名为决策树方案。

ID3

1970年代，一个叫昆兰的人找到了用信息论中的熵来度量决策树的决策选择过程，方法一出，它的简洁和高效就引起了轰动，昆兰把这个算法叫做ID3。它基于奥卡姆剃刀原理的，即用尽量用较少的东西做更多的事。ID3算法的核心思想就是以信息增益来度量属性的选择，选择分裂后信息增益最大的属性进行分裂。该算法采用自顶向下的贪婪搜索遍 历可能的决策空间。

要了解ID3，首先再回顾一下信息熵的概念。熵度量了事物的不确定性，越不确定的事物，它的熵就越大。具体的，随机变量X的熵的表达式如下： [math]\displaystyle{ H(X) = -\sum\limits_{i=1}^{n}p_i logp_i }[/math] 其中n代表X的n种不同的离散取值。而π代表了X取值为i的概率。举个例子，比如X有2个可能的取值，而这两个取值各为1/2时X的熵最大，此时X具有最大的不确定性。

下给出两个变量X和Y的联合熵表达式： [math]\displaystyle{ H(X,Y) = -\sum\limits_{i=1}^{n}p(x_i,y_i)logp(x_i,y_i) }[/math] 有了联合熵，又可以得到条件熵的表达式H(X|Y)，条件熵类似于条件概率,它度量了我们的X在知道Y以后剩下的不确定性。表达式如下： [math]\displaystyle{ H(X|Y) = -\sum\limits_{i=1}{n}p(x_i,y_i)logp(x_i|y_i) = \sum\limits_{j=1}{n}p(y_j)H(X|y_j) }[/math]

H(X)度量了X的不确定性，条件熵H(X|Y)度量了我们在知道Y以后X剩下的不确定性，那么H(X)-H(X|Y)度量了X在知道Y以后不确定性减少程度，这个度量在信息论中称为互信息。在决策树ID3算法中叫做信息增益。ID3算法就是用信息增益来判断当前节点应该用什么特征来构建决策树。信息增益大，则越适合用来分类。

ID3算法就是用信息增益大小来判断当前节点应该用什么特征来构建决策树，用计算出的信息增益最大的特征来建立决策树的当前节点。

举例

举一个信息增益计算的具体的例子。比如我们有15个样本D，输出为0或者1。其中有9个输出为0， 6个输出为1。 样本中有个特征A，取值为A1，A2和A3。在取值为A1的样本的输出中，有3个输出为1， 2个输出为0，取值为A2的样本输出中,2个输出为1,3个输出为0， 在取值为A3的样本中，4个输出为1，1个输出为0。 样本D的熵为：[math]\displaystyle{ H(D) = -(\frac{9}{15}log_2\frac{9}{15} + \frac{6}{15}log_2\frac{6}{15}) = 0.971 }[/math] 样本D在特征下的条件熵为：[math]\displaystyle{ H(D|A) = \frac{5}{15}H(D1) + \frac{5}{15}H(D2) + \frac{5}{15}H(D3) }[/math] 对应的信息增益为:[math]\displaystyle{ I(D,A) = H(D) - H(D|A) = 0.083 }[/math]

算法过程

算法的过程为：

• 初始化信息增益的阈值ϵ

• 判断样本是否为同一类输出Di，如果是则返回单节点树T。标记类别为Di

• 判断特征是否为空，如果是则返回单节点树T，标记类别为样本中输出类别D实例数最多的类别。

• 计算A中的各个特征（一共n个）输出D的信息增益，选择信息增益最大的特征Ag

• 如果Ag的信息增益小于阈值ϵ，则返回单节点树T，标记类别为样本中输出类别D实例数最多的类别。

• 否则，按特征Ag的不同取值Agi将对应的样本输出D分成不同的类别Di。每个类别产生一个子节点。对应特征值为Agi。返回增加了节点的数T。

• 对于所有的子节点，令D=Di,A=A−{Ag}递归调用，得到子树Ti并返回。

缺点

ID3算法虽然提出了新思路，但是还是有很多值得改进的地方。

• ID3没有考虑连续特征

• ID3采用信息增益大的特征优先建立决策树的节点。很快就被人发现，在相同条件下，取值比较多的特征比取值少的特征信息增益大。比如一个变量有2个值，各为1/2，另一个变量为3个值，各为1/3，其实他们都是完全不确定的变量，但是取3个值的比取2个值的信息增益大。如果校正这个问题呢？

• ID3算法对于缺失值的情况没有做考虑

• 没有考虑过拟合的问题

C4.5

ID3 算法的作者昆兰基于上述不足，对ID3算法做了改进，这就是C4.5算法。ID3算法有四个主要的不足，一是不能处理连续特征，第二个就是用信息增益作为标准容易偏向于取值较多的特征，最后两个是缺失值处理的问和过拟合问题。昆兰在C4.5算法中改进了上述四个问题。

对于不能处理连续特征这一不足， C4.5的思路是将连续的特征离散化。比如m个样本的连续特征A有m个，从小到大排列为a1,a2,...,am,则C4.5取相邻两样本值的中位数，一共取得m-1个划分点，其中第i个划分点Ti表示为[math]\displaystyle{ T_i = \frac{a_i+a_{i+1}}{2} }[/math]对于这m-1个点，分别计算以该点作为二元分类点时的信息增益。选择信息增益最大的点作为该连续特征的二元离散分类点。比如取到的增益最大的点为at,则小于at的值为类别1，大于at的值为类别2，这样我们就做到了连续特征的离散化。要注意的是，与离散属性不同的是，如果当前节点为连续属性，则该属性后面还可以参与子节点的产生选择过程。

对于信息增益作为标准容易偏向于取值较多的特征的问题,引入一个信息增益比的变量IR(X,Y)，它是信息增益和特征熵的比值。表达式如下： [math]\displaystyle{ I_R(D,A) = \frac{I(A,D)}{H_A(D)} }[/math]

其中D为样本特征输出的集合，A为样本特征，对于特征熵[math]\displaystyle{ H_A(D) }[/math],表达式如下： 其中n为特征A的类别数，Di为特征A的第i个取值对应的样本个数，D为样本个数。

特征数越多的特征对应的特征熵越大，作为分母，可以校正信息增益容易偏向于取值较多的特征的问题。

对于第三个缺失值处理的问题，主要需要解决的是两个问题，一是在样本某些特征缺失的情况下选择划分的属性，二是选定了划分属性，对于在该属性上缺失特征的样本的处理。

对于第一个子问题，对于某一个有缺失特征值的特征A。C4.5的思路是将数据分成两部分，对每个样本设置一个权重（初始可以都为1），然后划分数据，一部分是有特征值A的数据D1，另一部分是没有特征A的数据D2. 然后对于没有缺失特征A的数据集D1来和对应的A特征的各个特征值一起计算加权重后的信息增益比，最后乘上一个系数，这个系数是无特征A缺失的样本加权后所占加权总样本的比例。

对于第二个子问题，可以将缺失特征的样本同时划分入所有的子节点，不过将该样本的权重按各个子节点样本的数量比例来分配。比如缺失特征A的样本a之前权重为1，特征A有3个特征值A1,A2,A3。 三个特征值对应的无缺失A特征的样本个数为2,3,4.则a同时划分入A1，A2，A3。对应权重调节为2/9,3/9, 4/9。

对于第四个问题，C4.5引入了正则化系数进行初步的剪枝。

C5.0

该算法从ID3,C4.5改进而来。

• 分支准则：ID3使用熵减收益作为准则，从C4.5开始使用熵减值与分支导致的熵增的比例作为准则（单节点纯度为0，分为多节点即带来熵增）
• 分支数：2（ID3命名由此得来：Iterative Dichotomizer v3，决定了这是一个迭代二分支算法）
• 叶节点大小：75
• 分支最大深度：15
• C5.0嵌入了大规模学习常用的推进法

CART(Classification and Regression Tree)基尼分类树算法

在ID3算法中使用了信息增益来选择特征，信息增益大的优先选择。在C4.5算法中，采用了信息增益比来选择特征，以减少信息增益容易选择特征值多的特征的问题。但是无论是ID3还是C4.5,都是基于信息论的熵模型的，这里面会涉及大量的对数运算。能不能简化模型同时也不至于完全丢失熵模型的优点呢？

故引入了CART分类树算法。该算法使用基尼系数来代替信息增益比，基尼系数代表了模型的不纯度，基尼系数越小，则不纯度越低，特征越好。这和信息增益(比)是相反的。具体的，在分类问题中，假设有K个类别，第k个类别的概率为[math]\displaystyle{ p_k }[/math], 则基尼系数的表达式为：

[math]\displaystyle{ Gini(p) = \sum\limits_{k=1}{K}p_k(1-p_k) = 1- \sum\limits_{k=1}{K}p_k^2 }[/math]

如果是二类分类问题,属于第一个样本输出的概率是p，则基尼系数的表达式为： [math]\displaystyle{ Gini(p)=2p(1−p) }[/math]

CART分类树算法

算法输入是训练集D，基尼系数的阈值，样本个数阈值，输出是决策树T。

该算法从根节点开始，用训练集递归的建立CART树。

（1）对于当前节点的数据集为D，如果样本个数小于阈值或者没有特征，则返回决策子树，当前节点停止递归。

（2）计算样本集D的基尼系数，如果基尼系数小于阈值，则返回决策树子树，当前节点停止递归。

（3）计算当前节点现有的各个特征的各个特征值对数据集D的基尼系数，对于离散值和连续值的处理方法和基尼系数的计算见第二节。缺失值的处理方法和上篇的C4.5算法里描述的相同。

（4）在计算出来的各个特征的各个特征值对数据集D的基尼系数中，选择基尼系数最小的特征A和对应的特征值a。根据这个最优特征和最优特征值，把数据集划分成两部分D1和D2，同时建立当前节点的左右节点，做节点的数据集D为D1，右节点的数据集D为D2.

（5）对左右的子节点递归的调用1-4步，生成决策树。

对于生成的决策树做预测的时候，假如测试集里的样本A落到了某个叶子节点，而节点里有多个训练样本。则对于A的类别预测采用的是这个叶子节点里概率最大的类别。

缺点

（1）无论是ID3, C4.5还是CART,在做特征选择的时候都是选择最优的一个特征来做分类决策，但是大多数，分类决策不应该是由某一个特征决定的，而是应该由一组特征决定的。这样绝息到的决策树更加准确。这个决策树叫做多变量决策树 multi-variate decision tree 。在选择最优特征的时候，多变量决策树不是选择某一个最优特征，而是选择最优的一个特征线性组合来做决策。这个算法的代表是OC1，这里不多介绍。

（2）如果样本发生一点点的改动，就会导致树结构的剧烈改变。这个可以通过集成学习里面的随机森林之类的方法解决。

一些参数

• 分支准则: Gini不纯度改进
• 分支数：2
• 叶节点大小：60个观测
• 分支最大深度：10层
• 缺失值推断：2次
• 后向剪枝：ASE

CHAID （CHi-squared Automatic Interaction Detection)

• 分支准则：Pearson卡方检验，显著性 1e-5，使用Kass P调整
• 分支数：<=6
• 节点大小：150
• 模型选择：因为存在前剪枝，使用最大树

分析实例

Analysis can take into account the decision maker's (e.g., the company's) preference or utility function, for example: 决策分析可以考虑决策者(又譬如公司)的偏好或效用函数，例如:

文件:RiskPrefSensitivity2Threshold.png

The basic interpretation in this situation is that the company prefers B's risk and payoffs under realistic risk preference coefficients (greater than $400K—in that range of risk aversion, the company would need to model a third strategy, "Neither A nor B"). 对于图中的情况，基本的解释是：对于现实风险偏好系数和产品A/B进行分析，公司偏好产品B的风险和偿付。当超过400K这一风险规避范围内时，公司将需要模拟第三种战略，即“既非a也非B”。

Another example, commonly used in operations research courses, is the distribution of lifeguards on beaches (a.k.a. the "Life's a Beach" example). The example describes two beaches with lifeguards to be distributed on each beach. There is maximum budget B that can be distributed among the two beaches (in total), and using a marginal returns table, analysts can decide how many lifeguards to allocate to each beach. Another example, commonly used in operations research courses, is the distribution of lifeguards on beaches (a.k.a. the "Life's a Beach" example).[4] The example describes two beaches with lifeguards to be distributed on each beach. There is maximum budget B that can be distributed among the two beaches (in total), and using a marginal returns table, analysts can decide how many lifeguards to allocate to each beach. 在运筹学课程中经常使用的另一个例子是海滩上的救生员分布(又称“生活是海滩”的例子)。这个例子描述了两个海滩，每个海滩上都有救生员。在这两个海滩上(总共)可以分配的最多的救生员是B个，利用边际收益表，分析师可以决定每个海滩分配多少个救生员。

Lifeguards on each beach	Drownings prevented in total, beach #1	Drownings prevented in total, beach #2
1	1	3
2	4	0

In this example, a decision tree can be drawn to illustrate the principles of diminishing returns on beach #2. 在该例子下，可以绘制一个决策树来说明海滩#1、海滩#2的收益递减原则。

 --趣木木（讨论）该句有改动 觉得表达的意思是 绘制海滩一号、二号的收益表

文件:Beachdecisiontree.png

Beach Decision Tree

The decision tree illustrates that when sequentially distributing lifeguards, placing a first lifeguard on beach #1 would be optimal if there is only the budget for 1 lifeguard. But if there is a budget for two guards, then placing both on beach #2 would prevent more overall drownings. 该决策树表明，当按顺序分配救生员时，如果只能配有一名救生员，那么在海滩#1上部署该名救生员将是最优选择。但是如果能配有两名救生员，那么将他们都部署在海滩#2可以防止更多的溺水事件。

文件:Lifeguards.png

Lifeguards

关联规则归纳

Main article: Decision tree learning Decision trees can also be seen as generative models of induction rules from empirical data. An optimal decision tree is then defined as a tree that accounts for most of the data, while minimizing the number of levels (or "questions"). Several algorithms to generate such optimal trees have been devised, such as ID3/4/5, CLS, ASSISTANT, and CART.

Main article: Decision tree learning Decision trees can also be seen as generative models of induction rules from empirical data. An optimal decision tree is then defined as a tree that accounts for most of the data, while minimizing the number of levels (or "questions").[5] Several algorithms to generate such optimal trees have been devised, such as ID3/4/5,[6] CLS, ASSISTANT, and CART. 主要文章:决策树学习 决策树也可以看作是经验数据归纳规则的生成模型。将最优决策树定义为一个树，它负责大部分数据，同时最小化“问题”的数量。已经有了几种生成该种最优树的算法，如ID3/4/5、[6]CLS、ASSISTANT和CART。

 --趣木木（讨论） while minimizing the number of levels (or "questions") 中的level想理解为决策树的层数  但是感觉比较赘余  故未翻译levels

优缺点

决策树的优点

Among decision support tools, decision trees (and influence diagrams) have several advantages. Decision trees: 在决策支持工具中，决策树(和影响图)有几个优点。 决策树:

• Are simple to understand and interpret. People are able to understand decision tree models after a brief explanation.
• Have value even with little hard data. Important insights can be generated based on experts describing a situation (its alternatives, probabilities, and costs) and their preferences for outcomes.
• Help determine worst, best and expected values for different scenarios.
• Use a white box model. If a given result is provided by a model.
• Can be combined with other decision techniques.
• 简单直观，易于理解和解释。仅通过简单的解释，人们就能够理解决策树模型。
• 即使很少的数据也有价值。对于数据的见解可以基于专家描述的情况(其选择、可能性和成本)和对结果的偏好。
• 帮助确定最坏的、最好的和不同场景下的期望值。
• 相比于神经网络之类的黑盒分类模型，如果一个给定的结果是由一个模型提供的,决策树使用白盒模型,其在逻辑上可以得到很好的解释。
• 可以与其他决策技术相结合进行决策分析。

 --趣木木（讨论）下补充一些优缺点，上面对白盒模型 相对的黑盒分类模型也进行了一些解释

• 基本不需要预处理，不需要提前归一化，处理缺失值。
• 既可以处理离散值也可以处理连续值。（很多算法只是专注于离散值或者连续值。）
• 可以处理多维度输出的分类问题。
• 可以交叉验证的剪枝来选择模型，从而提高泛化能力。
• 对于异常点的容错能力好，健壮性高。

决策树的缺点

Disadvantages of decision trees:

• They are unstable, meaning that a small change in the data can lead to a large change in the structure of the optimal decision tree.
• They are often relatively inaccurate. Many other predictors perform better with similar data. This can be remedied by replacing a single decision tree with a random forest of decision trees, but a random forest is not as easy to interpret as a single decision tree.
• For data including categorical variables with different number of levels, information gain in decision trees is biased in favor of those attributes with more levels.
• Calculations can get very complex, particularly if many values are uncertain and/or if many outcomes are linked.

• They are unstable, meaning that a small change in the data can lead to a large change in the structure of the optimal decision tree.
• They are often relatively inaccurate. Many other predictors perform better with similar data. This can be remedied by replacing a single decision tree with a random forest of decision trees, but a random forest is not as easy to interpret as a single decision tree.
• For data including categorical variables with different number of levels, information gain in decision trees is biased in favor of those attributes with more levels.[7]
• Calculations can get very complex, particularly if many values are uncertain and/or if many outcomes are linked.
• 其不稳定，这意味着决策树会因为样本发生一点点的改动，就会导致树结构的剧烈改变。这个可以通过集成学习之类的方法解决。
• 其通常是相对不准确的。许多其他预测器在处理类似数据时表现得更好。这可以通过用决策树的随机森林替换单个决策树来补救，但是随机森林不像单个决策树那样容易解释。
• 对于包含不同层次数量的分类变量的数据，决策树中的信息增益更倾向于层次数量更多的属性[7]
• 计算会变得非常复杂。特别是在许多结果是相互关联的情况下，许多值是不确定的和/或关系的时候计算会十分复杂。可以换神经网络分类方法来解决。

 --趣木木（讨论）补充缺点

• 决策树算法非常容易过拟合，导致泛化能力不强。可以通过设置节点最少样本数量和限制决策树深度来改进。
• 寻找最优的决策树是一个十分难的问题，我们一般是通过启发式方法，容易陷入局部最优。可以通过集成学习之类的方法来改善。
• 如果某些特征的样本比例过大，生成决策树容易偏向于这些特征。这个可以通过调节样本权重来改善。

决策树的大规模训练

附上一些关于决策树的应用实例 File:car 实例运用到bagging、dtree、randomforest算法.zip
File:car的另一实例 运用到randomforest、dtree算法.zip
File:party实例 运用到randomforest、dtw、bagging算法.zip

交叉验证(Cross Validation)

利用独立的验证数据集，测试子树序列[math]\displaystyle{ T_0,T_1,...,T_n }[/math]当中各棵子树的平方误差或者基尼不纯度。平方误差或者基尼不纯度最小的决策树被认为是最优的决策树。另外，在子树序列当中，每棵子树T都对应一个参数[math]\displaystyle{ α }[/math]。所以，当最优子树[math]\displaystyle{ T_k }[/math]确定的时候，对应的[math]\displaystyle{ α_k }[/math]也就确定了。

袋装法(Bagging)

集成学习有两个流派，一个是Boosting派系，它的特点是各个弱学习器之间有依赖关系。另一种是Bagging流派，它的特点是各个弱学习器之间没有依赖关系，可以并行拟合。

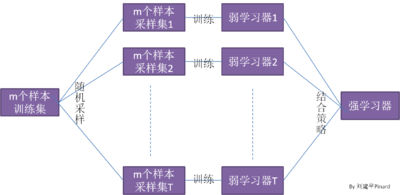
Bagging的原理图为下图。

在Bagging原理中不得不提自助采样法。 自助采样法 Bootsrap就是从我们的训练集里面采集固定个数的样本，但是每采集一个样本后，都将样本放回。也就是说，之前采集到的样本在放回后有可能继续被采集到。对于我们的Bagging算法，一般会随机采集和训练集样本数m一样个数的样本。这样得到的采样集和训练集样本的个数相同，但是样本内容不同。如果我们对有m个样本训练集做T次的随机采样，则由于随机性，T个采样集各不相同。

注意到这和GBDT的子采样是不同的。GBDT的子采样是无放回采样，而Bagging的子采样是放回采样。

对于一个样本，它在某一次含m个样本的训练集的随机采样中，每次被采集到的概率是[math]\displaystyle{ \frac{1}{m} }[/math],不被采集到的概率为[math]\displaystyle{ 1-\frac{1}{m} }[/math],如果m次采样都没有被采集中的概率是[math]\displaystyle{ (1-\frac{1}{m})m }[/math],当[math]\displaystyle{ m \to \infty }[/math],[math]\displaystyle{ (1-\frac{1}{m})m \to \frac{1}{e} \simeq 0.368 }[/math],在Bagging的每轮随机采样中，训练集中大约有36.8%的数据没有被采样集采中。

照这样，我们可采样出T个含m个训练样本的采样集，然后基于每个采样集训练出一个基学习器，再将这些基学习器进行结合，这就是Bagging的基本流程、在对预测输出进行结合时，Bagging通常对分类任务使用简单投票法，对回归任务使用简单平均法、若分类预测时出现两个类收到同样票数的情形，则最简单的做法是随机选择-一个, 也可进一步考察学习器投票的置信度来确定最终胜者。

推进法(Boosting)

File:boost.zip

Boosting算法要求基学习器能对特定的数据分布进行学习，这可通过“重赋权法” re-weighting 实现,即在训练过程的每一轮中, 根据样本分布为每个训练样本重新赋予-一个权重。对无法接受带权样本的基学习算法，则可通过“重采样法” re-sampling 来处理,即在每一轮学习中,根据样本分布对训练集重新进行采样,再用重采样而得的样本集对基学习器进行训练。一般而言，这两种做法没有显著的优劣差别。需注意的是，Boosting 算法在训练的每一轮都要检查当前生成的基学习器是否满足基本条件，一旦条件不满足，则当前基学习器即被抛弃,且学习过程停止。在此种情形下，初始设置的学习轮数T也许还远未达到，可能导致最终集成中只包含很少的基学习器而性能不佳。若采用“重采样法”，则可获得“重启动”机会以避免训练过程过早停止，即在抛弃不满足条件的当前基学习器之后,可根据当前分布重新对训练样本进行采样,再基于新的采样结果重新训练出基学习器,从而使得学习过程可以持续到预设的T轮完成。从偏差-方差分解的角度看，Boosting 主要关注降低偏差,因此Boosting能基于泛化性能相当弱的学习器构建出很强的集成。

Boosting算法的工作机制是首先从训练集用初始权重训练出一个弱学习器1，根据弱学习的学习误差率表现来更新训练样本的权重，使得之前弱学习器1学习误差率高的训练样本点的权重变高，进而使得这些误差率高的点在后面的弱学习器2中得到更多的重视。然后基本调整权重后的训练集来训练弱学习器2，如此重复进行，直到弱学习器数达到事先指定的数目T，最终将这T个弱学习器通过集合策略进行整合，得到最终的强学习器。

Boosting系列算法里最著名算法主要有AdaBoost算法和提升树 Boosting tree 系列算法，提升树系列算法里面应用最广泛的是梯度提升树 Gradient Boosting Tree。

AdaBoosting 算法

Adaboost既可以用作分类，也可以用作回归。 Boosting算法中，有四个问题需要解决。

1）如何计算学习误差率e?

2) 如何得到弱学习器权重系数α?

3）如何更新样本权重D?

4) 使用何种结合策略？

算法

假设训练集样本是[math]\displaystyle{ T={(x_1,y_1),(x_2,y_2), ...(x_m,y_m)} }[/math],训练集的在第k个弱学习器的输出权重为[math]\displaystyle{ D(k) = (w_{k1}, w_{k2}, ...w_{km}) ;;; w_{1i}=\frac{1}{m};;; i =1,2...m }[/math]。

首先看看Adaboost的分类问题，分类问题的误差率很好理解和计算。由于多元分类是二元分类的推广，这里假设是二元分类问题，输出为{-1，1}，则第k个弱分类器[math]\displaystyle{ G_k(x) }[/math],在训练集上的加权误差率为[math]\displaystyle{ e_k = P(G_k(x_i) \neq y_i) = \sum\limits_{i=1}^{m}w_{ki}I(G_k(x_i) \neq y_i) }[/math]。

对于二元分类问题如何得到弱学习器权重系数α的第二类问题，第k个弱分类器[math]\displaystyle{ G_k(x) }[/math]的权重系数为[math]\displaystyle{ \alpha_k = \frac{1}{2}log\frac{1-e_k}{e_k} }[/math] 从上式可以看出，如果分类误差率[math]\displaystyle{ e_k }[/math]越大，则对应的弱分类器权重系数[math]\displaystyle{ α_k }[/math]越小。也就是说，误差率小的弱分类器权重系数越大。

对于第三个问题，更新样本权重D，假设第k个弱分类器的样本集权重系数为[math]\displaystyle{ D(k) = (w_{k1}, w_{k2}, ...w_{km}) }[/math],则对应的第k+1个弱分类器的样本集权重系数为[math]\displaystyle{ w_{k+1,i} = \frac{w_{ki}}{Z_K}exp(-\alpha_ky_iG_k(x_i)) }[/math],[math]\displaystyle{ Z_k }[/math]是规范化因子[math]\displaystyle{ Z_k = \sum\limits_{i=1}^{m}w_{ki}exp(-\alpha_ky_iG_k(x_i)) }[/math]。

从[math]\displaystyle{ w_{k+1,i} }[/math]的式子中看出，如果第i个样本分类错误，则[math]\displaystyle{ y_iG_k(x_i) \lt 0 }[/math],导致样本的权重在第k+1个弱分类器中增大，如果分类正确，则权重在第k+1个弱分类器中减少。

Adaboost分类采用的是加权平均法，最终的强分类器为[math]\displaystyle{ f(x) = sign(\sum\limits_{k=1}^{K}\alpha_kG_k(x)) }[/math]

对于采取何种结合策略，和分类问题一样，采用的也是加权平均法，最终的强回归器为[math]\displaystyle{ f(x) = \sum\limits_{k=1}^{K}(ln\frac{1}{\alpha_k})G_k(x) }[/math]。

辅助功能

• 变量选择
• 变量离散化
• 离散化程度降低
• 交互作用检测
• 分层回归
• 回归缺失值补齐

决策树剪枝的部分介绍

决策树是充分考虑了所有的数据点而生成的复杂树，有可能出现过拟合的情况，决策树越复杂，过拟合的程度会越高。

考虑极端的情况，如果令所有的叶子节点都只含有一个数据点，那么我们能够保证所有的训练数据都能准确分类，但是很有可能得到高的预测误差，原因是将训练数据中所有的噪声数据都”准确划分”了，强化了噪声数据的作用。

剪枝修剪分裂前后分类误差相差不大的子树，能够降低决策树的复杂度，降低过拟合出现的概率

剪枝类型

先剪枝和后剪枝，先剪枝指提前停止决策树的生长，后剪枝指在决策树生长完成之后再进行剪枝。

后剪枝

REP—错误率降低剪枝

顾名思义，该剪枝方法是根据错误率进行剪枝，如果一棵子树修剪前后错误率没有下降，就可以认为该子树是可以修剪的。REP剪枝需要用新的数据集，原因是如果用旧的数据集，不可能出现分裂后的错误率比分裂前错误率要高的情况。由于使用新的数据集没有参与决策树的构建，能够降低训练数据的影响，降低过拟合的程度，提高预测的准确率。

PEP—悲观剪枝

悲观剪枝认为如果决策树的精度在剪枝前后没有影响的话，则进行剪枝。即如果剪枝后的误差小于剪枝前经度的上限，则说明剪枝后的效果与剪枝前的效果一致，此时要进行剪枝。

CCP—代价复杂度剪枝

代价复杂度选择节点表面误差率增益值最小的非叶子节点，删除该非叶子节点的左右子节点。若有多个非叶子节点的表面误差率增益值相同小，则选择非叶子节点中子节点数最多的非叶子节点进行剪枝。

参见

• Behavior tree (artificial intelligence, robotics and control) 行为树(人工智能、机器人和控制)
• Boosting (machine learning)提高(机器学习）
• Decision cycle决策圈
• Decision list决策列表
• Decision table决策表
• Decision tree model决策树模型 of computation
• Design rationale 设计原理
• [DRAKON]]
• Markov chain马尔科夫链
• Random forest随机森林
• Odds algorithm概率算法
• Topological combinatorics拓扑组合
• Truth table真值表

相关链接

• Extensive Decision Tree tutorials and examples 广义决策树教程和例子
• Gallery of example decision trees 决策树的图库示例
• Gradient Boosted Decision Trees 梯度增强决策树

参考文献

• 决策树系列--剪枝
• 机器学习原理 决策树

编者推荐

书籍推荐

• 实用机器学习
• Python机器学习实践指南

视频推荐

• 机器学习思维
• 机器学习第二阶段：机器学习经典算法（2）——决策树与随机森林

文章推荐

• 决策树
• 决策树的复兴？结合神经网络，提升ImageNet分类准确率且可解释
• 结合机器学习和社会网络分析揭示组织结构中利用到随机森林和决策树算法]