网络科学

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
（重定向自信息生产:网络科学）
跳到导航 跳到搜索

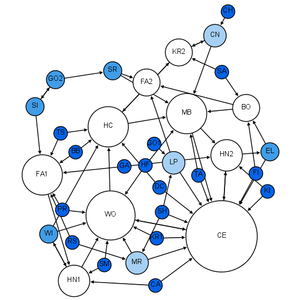
网络科学 Network Science是一个研究复杂网络的学术领域，如通讯网络，计算机网络，生物网络，认知和语义网络，以及社会网络，主要由节点（顶点）表示不同元素或参与者，由连边表示元素或参与者之间的联系。该领域借鉴了数学中的图论，物理学中的统计力学，计算机科学中的数据挖掘和信息可视化，统计学中的推理建模和社会学中的社会结构等理论和方法。 美国国家研究委员会 The United States National Research Council将网络科学定义为“研究物理、生物和社会现象的网络表征，从而得出这些现象的预测模型。” [1]

背景和历史

网络研究作为分析复杂关系型数据的一种手段，在不同的学科中都有出现。在这个领域已知最早的论文是1736年欧拉 Leonhard Euler所写的著名的《哥尼斯堡的七座桥 Seven Bridges of Königsberg》。欧拉对顶点和边的数学描述是图论的基础，图论是研究网络结构中的成对关系属性的数学分支。图论的领域不断发展，并在化学中得到应用。


匈牙利数学家兼教授Dénes Kőnig在1936年撰写了第一本图论专著《有限图与无限图的理论 Theory of finite and infinite graphs》。 [2]


莫雷诺的一年级社交图。

20世纪30年代，格式塔传统的心理学家雅各布·莫雷诺 Jacob Moreno来到美国。他提出了社会人际关系图 sociogram这一概念，并在1933年4月的一次医学学者大会上向公众展示了他制作的社会人际关系图。Moreno声称，“在社会计量学出现之前，没有人知道一个群体的人际关系结构‘精确的’样子”。这张社会图展示了一组小学生的社会结构。男孩是男孩的朋友，女孩是女孩的朋友，只有一个男孩说他喜欢另一个单身女孩但是没有得到回应。这个网络展示的社会结构非常有趣，也被刊登在《纽约时报》上（1933年4月3日，第17页）。社会图已经有许多的应用场景，并且已经发展成为社会网络分析 social network analysis的一个子领域。


20世纪90年代，在Paul Erdős和Alfréd Rényi发表了8篇关于随机图的著名论文之后，网络科学中的概率论 Probabilistic theory作为图论的一个分支发展起来了。对于社交网络 social network来说，指数随机图模型或[math]\displaystyle{ p* }[/math]是一个记号框架，用于表示社交网络中发生关系的概率空间。网络概率结构的另一种替代表示方法是网络概率矩阵，它根据网络样本中边的历史信息来计算这条边在网络中出现的概率。


1998年，David Krackhardt和Kathleen Carley提出了用PCANS模型构建元网络 meta-network的想法。他们认为，“所有的组织都是按照‘个人、任务和资源’这三个领域来构建的”。他们的论文介绍了新的网络概念，即网络发生在多个领域且相互关联。这个领域也已经发展成为网络科学的另一个子学科，即动态网络分析 dynamic network analysis。


最近，其他网络科学的研究致力于用数学的方式描述不同网络的拓扑结构。邓肯·瓦茨 Duncan J.Watts将网络的经验数据与数学表达相结合，描述了小世界网络。 艾伯特-拉斯洛·巴拉巴西 Albert-László Barabási 和 Reka Albert提出了无标度网络，这是一种定义不明确的网络拓扑结构，简单说就是包含Hub中心节点（连边数量很多的节点），且连边的数量和节点数量呈现常数比率的增长方式。尽管许多网络，比如互联网，似乎保持了这样的特性，但是其他网络的节点分布表现出长尾特性，仅仅是接近无标度比例。


国防部倡议

1996年，美国军方第一次对网络中心战感兴趣，将其作为一个基于网络科学的军事概念。2003年12月1日，美国陆军研究和实验室管理主任 John A. Parmentola 向军队的科学和技术委员会 BAST提出，网络科学成为一个新的军事研究领域。科学和技术委员会是美国国家学院国家研究委员会 NRC工程和物理科学司的下属部门，主要讨论对军队重要的科学和技术问题，并监督美国国家学院进行的军队相关的独立研究。科学和技术委员会进行了一项研究，他们想知道确定和资助网络科学这一新的研究领域的基础研究，能否帮助缩小实现网络中心战所需的资源与当前网络基础知识的原始状态之间的差距。


因此，科学和技术委员在2005年发布了题为《网络科学》（见上文）的NRC研究报告，为军队网络科学的基础研究开辟了一个新领域。基于这项研究的发现和建议，以及随后在2007年NRC发布的题为《军队网络科学、技术和实验中心战略》的研究报告，军队基础研究资源被重新分配，以启动新的网络科学基础研究计划。为构建复杂网络的全新理论基础，美国陆军实验室目前正在进行的一些关键的网络科学研究工作致力于:

  • 网络行为的数学模型，以预测网络规模、复杂度和环境的表现
  • 网络化战争所需的最佳人为表现
  • 生态系统中基于细胞分子层面的网络建模


正如2004年，David S. Alberts支持Frederick I. Moxley那样，国防部帮助美国陆军一起在美国军事学院（USMA）建立了第一个网络科学中心。在Moxley博士和美国军事学院研究员的指导下，西点军校开设了首个跨学科的网络科学本科生课程。为了更好地在其未来的领导干部中灌输网络科学的原则，美国军事学院还在网络科学下设置了一个5节课的本科生辅修课程。


2006年，美国陆军和英国成立了网络和信息科学国际技术联盟，这是美国陆军研究实验室、英国国防部以及美国和英国的工业和大学联盟之间的合作伙伴关系。该联盟的目标是进行基础研究，以支持两国需要的网络中心作战。


2009年，美军成立了网络科学 CTA，这是一个由陆军研究实验室、 CERDEC 和美国大约30个工业研发实验室和大学组成的联盟之间的合作研究联盟。这个联盟的目标是深入理解交织在一起的社会 / 认知、信息和通信网络之间的潜在共性，从而提高我们分析、预测、设计和影响交织在多种网络中的复杂系统的能力。


随后，作为这些努力的结果，美国国防部赞助了许多支持网络科学的研究项目。


网络性质

通常，网络具有一些可计算的属性来分析网络的性质和特征。这些网络性质的特征通常被定义为网络模型 ，可用于对比分析不同模型之间的差异。网络科学中使用的许多其他术语可以在图论术语表Glossary of graph theory中找到相关定义。


规模

网络的规模可以指节点的个数[math]\displaystyle{ N }[/math]，或者，少数情况下，连边的数量[math]\displaystyle{ E }[/math]（对于没有重边的连通图），连边的数量[math]\displaystyle{ E }[/math]一般从[math]\displaystyle{ N-1 }[/math] （看做是一个树）到[math]\displaystyle{ E_{\max} }[/math] （看做是一个完全图）不等。在简单图（网络中在每对节点之间至多存在一条（无向）边，并且没有节点连向自己）的例子中，可以计算[math]\displaystyle{ E_{\max}=\tbinom N2=N(N-1)/2 }[/math]；对于有向图（没有自环节点）而言，[math]\displaystyle{ E_{\max}=N(N-1) }[/math]；对于有向图且允许存在自环节点的，[math]\displaystyle{ E_{\max}=N^2 }[/math]。而对于一对节点之间存在重边的情况，[math]\displaystyle{ E_{\max}=\infty }[/math]。


密度

网络的密度 [math]\displaystyle{ D }[/math] 通常定义为在具有 [math]\displaystyle{ N }[/math] 个节点的网络中，连边数量 [math]\displaystyle{ E }[/math] 与可能的连边数的比率，例如在简单图中，由二项式系数 [math]\displaystyle{ \tbinom N2 }[/math] 计算得出，则 [math]\displaystyle{ D =\frac{E-(N-1)}{Emax - (N-1)} = \frac{2(E-N+1)}{N(N-3)+2} }[/math]。另一个可能的等式为[math]\displaystyle{ D = \frac{T-2N+2}{N(N-3)+2} }[/math] ，而联系[math]\displaystyle{ T }[/math] 是单向的。这为网络密度提供了更好的概述，因为单向关系是可测量的。


平面网络密度

在连边之间没有交集的情况下，网络的密度 [math]\displaystyle{ D }[/math] 被定义为在具有 [math]\displaystyle{ N }[/math] 个节点的网络中，连边数量 [math]\displaystyle{ E }[/math] 与可能的连边数的比率，由没有交集连边的图给出 [math]\displaystyle{ (E_{\max}=3N-6) }[/math]，则 [math]\displaystyle{ D = \frac{E-N+1}{2N-5}. }[/math]


平均度

一个节点所连接的边数被称为节点的度 [math]\displaystyle{ k }[/math] 。与网络密度密切相关的是平均度， [math]\displaystyle{ \langle k\rangle = \tfrac{2E}{N} }[/math] （或者在一些有向图中， [math]\displaystyle{ \langle k\rangle = \tfrac{E}{N} }[/math]，前一个式子中多了一个2倍关系，是因为无向图中的每一条边形成了两个不同顶点的度）。在ER随机图模型([math]\displaystyle{ G(N,p) }[/math]) 中，我们可以计算[math]\displaystyle{ \langle k \rangle }[/math] 的期望值（等于随机点的期望值 [math]\displaystyle{ k }[/math]）：一个随机点在网络中有 [math]\displaystyle{ N-1 }[/math] 个其他可用顶点两两相连，相连的概率为[math]\displaystyle{ p }[/math]。因此，[math]\displaystyle{ \mathbb{E}[\langle k \rangle]=\mathbb{E}[k]= p(N-1) }[/math]。


平均最短路径长度（特征路径长度）

平均最短路径长度的计算方法是找到所有节点对之间的最短路径，并取其长度所有路径的平均值（其长度为路径中包含的中间边的数目，即图中两个顶点 [math]\displaystyle{ u,v }[/math] 之间的距离[math]\displaystyle{ d_{u,v} }[/math]）。这向我们展示了从网络中的一个成员到另一个成员所需的平均步数。期望平均最短路径长度（即平均最短路径长度的总体均值）作为随机网络模型的顶点数 [math]\displaystyle{ N }[/math] 的函数的行为定义了该模型是否表现出小世界效应；如果它变为 [math]\displaystyle{ O(\ln N) }[/math] ，则该模型生成小世界网络。对于比对数更快的增长，该模型不会产生小世界。[math]\displaystyle{ O(\ln\ln N) }[/math]的特例是超小世界效应。


网络直径

网络直径指的是网络中所有计算出来的最短路径中的最大值，它是另一种测量网络图的方法。它是网络中两个最远节点之间的最短距离。换言之，只要计算出来网络中每个节点到其他所有节点的最短路径长度，直径就是所有计算出的路径长度中最长的。网络直径代表网络的线性规模。假如网络的节点以A-B-C-D的方式连接，那么从A->D的路径长度3（3个跳跃，3个连接）就是这个网络的直径。


聚集系数

聚集系数是表示“我所有的朋友都互相认识”这样一种性质的指标。有时候也被表述为“我朋友的朋友也是我的朋友”。更准确地说，节点的聚类系数是该节点的相邻节点之间的现有连接数与其最大可能连接数之比。整个网络的聚集系数是所有节点的聚集系数的平均值。网络的高聚集系数是小世界实验的另一个标志。


第 [math]\displaystyle{ i }[/math] 个节点的聚集系数为:

[math]\displaystyle{ C_i = {2e_i\over k_i{(k_i - 1)}}\, }[/math]

其中 [math]\displaystyle{ k_i }[/math] 是第 [math]\displaystyle{ i }[/math] 个节点的相邻节点数， [math]\displaystyle{ e_i }[/math] 是这些相邻节点数之间的连接数。相邻节点之间的最大可能连接数为

[math]\displaystyle{ {\binom {k}{2}} = {{k(k-1)}\over 2}\, }[/math]


从概率的角度来看，期望的局部聚集系数是同一节点的任意两个相邻节点之间存在连接的可能性。


连通性

在分析和理解网络的过程中，网络的连接方式有着很重要的作用。网络可以分为以下四类：

  • 全连接图： 完全连接的网络，其中所有的节点之间都相互连接。这样的网络是对称的，每个节点都有其他所有节点的入边和出边。
  • 超大连通子图： 包含网络中大多数节点的单个连通子图。
  • 弱连通子图： 不考虑边的方向的情况下，任意两个节点之间都存在路径的子图。
  • 强连通子图： 任意两个节点间都存在有向路径的子图。

节点中心性

中心性指标可以给出所有节点的一个排序，用来寻找网络模型中最重要的节点。在不同的“重要性”的含义下，中心性指标也可以是不同的。例如介数中心性，在它的定义下，如果一个节点和其他很多节点之间都有连接，那么这个节点就是很重要的。而本征值中心性则相反，如果某个节点有很多很重要的节点与之相连，那么这个节点就是很重要的。文献中给出了数百种这样的中心性的定义。


中心性指数只能准确地识别最中心的节点，这些测量对其余的网络节点几乎没有意义。 [3] [4] 而且，这些指标只在它们所假定的重要性的含义下是准确的，而在其他重要性含义中往往是“错误的”。[5] 例如，假设有两个互相分离的团块，只在两个团块中较小成员之间存在一条边。由于从一个团块到另外一个团块的任何迁移都要通过这条边，因此这两个较小成员就会有很高的介数中心性。但是由于它们是重要性较低的成员，它们和“重要的”节点之间连接较少，这就意味着它们的本征值中心性较小。


基于经验和理论的研究，静态网络上定义的中心性的概念可以拓展到时序网络中的动态中心性。[6][7][8][9]


节点影响力

中心性测量的局限性促使了更加常规的测量的发展。其中两个例子分别是可达性，它利用随机行走的多样性去度量从一个节点出发到网络其余部分的可到达性；[10] 以及从一个节点的感染力的期望值中得到的期望力。[3] 这两种测量都可以仅从网络的结构中计算出来。

网络模型

网络模型是理解经验上复杂网络内相互作用的基础，各种各样的随机图生成的模型所产生的网络结构可与现实中的复杂网络进行比较。


Erdős–Rényi 随机图模型

该 ER随机图模型 由 N = 4 个节点生成。对于由所有 N 个节点构成的完整图中的每一条边，生成一个随机数，并与给定的概率进行比较。假如随机数小于 p ，则在模型上形成一条边。

以Paul Erdős和Alfréd Rényi命名的Erdős Rényi 模型用于生成随机图，它的边是等概率连接的节点的集合。随机图可以用来证明概率方法中满足某些条件的图的存在性，或者对几乎所有图给出某个性质的严格定义。


生成Erdős–Rényi模型 [math]\displaystyle{ G(n, p) }[/math]需要给定两个参数：总的节点数n，以及任意两个节点间有连接的概率p 。


由于模型是在不偏向特定节点的情况下生成的，因此度分布是二项分布：对任意的节点[math]\displaystyle{ v }[/math] ： [math]\displaystyle{ P(\deg(v) = k) = {n-1\choose k} p^k (1-p)^{n-1-k}. }[/math]


Erdős–Rényi 模型的聚集系数是0 a.s。 [math]\displaystyle{ G(n, p) }[/math] 的行为可以分为三个区域：

  1. 亚临界 [math]\displaystyle{ n p \lt 1 }[/math]: 所有分量都是简单而且很小的，其中最大分量的大小为 [math]\displaystyle{ |C_1| = O(\log n) }[/math];
  2. 临界 [math]\displaystyle{ n p = 1 }[/math]: [math]\displaystyle{ |C_1| = O(n^\frac{2}{3}) }[/math];
  3. 超临界[math]\displaystyle{ n p \gt 1 }[/math]:[math]\displaystyle{ |C_1| \approx yn }[/math] 其中 [math]\displaystyle{ y = y(n p) }[/math] 是方程 [math]\displaystyle{ e^{-p n y }=1-y }[/math]的正根。


最大的连通分量复杂性最高，其他所有分量都是简单而且很小的 [math]\displaystyle{ |C_2| = O(\log n) }[/math]。


配置模型

配置模型以一个度序列[11][12] 或度分布[13] （用于生成度序列）作为输入，生成除了度序列外各方面随机连接的图。这意味着对于给定的度序列，图是从符合这个度序列的所有图的集合中随机均匀地选择的。图中任意节点的度[math]\displaystyle{ k }[/math]是一个独立同分布的随机变量，其值为整数。当 [math]\displaystyle{ \mathbb E [k^2] - 2 \mathbb E [k]\gt 0 }[/math] 时，配置图包含超大连通分量，其大小是无穷。[12] 其他分量大小是有限的，可以用大小分布来定量表示。图中任意取的一个节点和大小为[math]\displaystyle{ n }[/math]的分量相连接的概率 [math]\displaystyle{ w(n) }[/math] 由度分布的卷积幂给出：[14][math]\displaystyle{ w(n)=\begin{cases} \frac{\mathbb E [k]}{n-1} u_1^{*n}(n-2),& n\gt 1, \\ u(0) & n=1. \end{cases} }[/math]其中 [math]\displaystyle{ u(k) }[/math] 表示度分布且 [math]\displaystyle{ u_1(k)=\frac{(k+1)u(k+1)}{\mathbb E[k]} }[/math]。 通过随机移除临界比例[math]\displaystyle{ p_c }[/math]的边，可以摧毁超大连通分量。这个过程叫做 随机网络的渗流。当度分布的二阶矩是有限的，即[math]\displaystyle{ \mathbb E [k^2]\lt \infty }[/math] 时，这个边数的临界比例为 [15] [math]\displaystyle{ p_c=1-\frac{\mathbb E[k]}{ \mathbb E [k^2] - \mathbb E[k]} }[/math] ，且超大连通分量中顶点与顶点间的平均距离[math]\displaystyle{ l }[/math] 的大小和网络的总规模呈对数比例， [math]\displaystyle{ l = O(\log N) }[/math].[13]。


在有向配置模型中，节点的度取决于两个量，入度[math]\displaystyle{ k_\text{in} }[/math] 和出度 [math]\displaystyle{ k_\text{out} }[/math]，因此度分布是二维的。入度和出度的期望值相等，即 [math]\displaystyle{ \mathbb E [k_\text{in}]=\mathbb E [k_\text{out}] }[/math]。有向配置模型中包含超大连通分量 iff[16][math]\displaystyle{ 2\mathbb{E}[k_\text{in}] \mathbb{E}[k_\text{in}k_\text{out}] - \mathbb{E}[k_\text{in}] \mathbb{E}[k_\text{out}^2] - \mathbb{E}[k_\text{in}] \mathbb{E}[k_\text{in}^2] +\mathbb{E}[k_\text{in}^2] \mathbb{E}[k_\text{out}^2] - \mathbb{E}[k_\text{in} k_\text{out}]^2 \gt 0. }[/math]注意 [math]\displaystyle{ \mathbb E [k_\text{in}] }[/math] 和 [math]\displaystyle{ \mathbb E [k_\text{out}] }[/math] 是相等的，因此在后面的不等式中二者可交换。对于图中任意一个节点，它属于大小为[math]\displaystyle{ n }[/math]的子图的概率由下式给出：

  • 入分量: [17][math]\displaystyle{ h_\text{in}(n)=\frac{\mathbb E[k_{in}]}{n-1} \tilde u_\text{in}^{*n}(n-2), \;n\gt 1, \; \tilde u_\text{in}=\frac{k_\text{in}+1}{\mathbb E[k_\text{in}]}\sum\limits_{k_\text{out}\geq 0}u(k_\text{in}+1,k_\text{out}) }[/math]
  • 出分量: [math]\displaystyle{ h_\text{out}(n)=\frac{\mathbb E[k_\text{out}]}{n-1} \tilde u_\text{out}^{*n}(n-2), \;n\gt 1, \;\tilde u_\text{out}=\frac{k_\text{out}+1}{\mathbb E[k_\text{out}]}\sum\limits_{k_\text{in}\geq0}u(k_\text{in},k_\text{out}+1). }[/math]


Watts–Strogatz 小世界模型

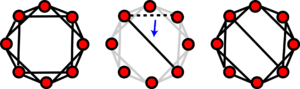
Watts–Strogatz 模型利用重连接的概念构造小世界网络结构。模型生成器会遍历初始晶格结构中的所有边，每一条边会以给定的重连接概率改变它两端的节点，例如[math]\displaystyle{ \langle k\rangle = 4 }[/math]。

Watts–Strogatz 模型是一个随机图生成模型，能够产生具有小世界性质的网络。


Watts–Strogatz 模型在一个初始的晶格结构的基础上生成。网络中每个节点最初都与它的 [math]\displaystyle{ \langle k\rangle }[/math] 个最近邻节点连接。给定另外一个参数为重连接概率，每条边以 [math]\displaystyle{ p }[/math] 的概率在图中随机重连。该模型中重连接边数的期望值为 [math]\displaystyle{ pE = pN\langle k\rangle/2 }[/math]。


由于Watts–Strogatz 模型的初始网络具有非随机的晶格结构，因此它具有很高的聚集系数和平均路径长度。每次重新连接都可能在高度连接的集群之间创建一条捷径。随着重连接概率的增加，聚集系数的下降速度慢于平均路径长度的下降速度。实际上，这使得网络的平均路径长度显著降低，而聚集系数只略微降低。更高的重连接概率[math]\displaystyle{ p }[/math]会导致更多的边重新连接，这实际上使Watts–Strogatz模型趋于随机网络。


Barabási–Albert BA优先链接模型

BA模型是一个随机网络模型，用于说明偏好依附效应（优先链接）或“富人越富”效应。在这个模型中，一条边最有可能附着在度数较高的节点上。这个网络从 m0节点的初始网络开始。 m0 ≥ 2时，初始网络中每个节点的度至少为 1，否则它将始终与网络的其余部分断开。


在BA模型中，每次向网络中添加一个新节点。每个新节点和已有的[math]\displaystyle{ m }[/math]个节点相连接，连接的概率与现有节点已拥有的连接数成正比。形式上，新节点与节点 i 相连的概率 pi 为 [18]

[math]\displaystyle{ p_i = \frac{k_i}{\sum_j k_j}, }[/math]

其中 ki 是节点 i 的度。大量连接的节点（“中心”）倾向于快速累积更多的连接，而只有少量连接的节点不太可能拥有新连接。新节点“偏好”将自己连接到已经高度连接的节点上。


BA模型的度分布服从幂律。在对数标度中幂律函数是一条直线。[19]

BA模型得到的度分布是无标度的，特别是它的形式是幂律：

[math]\displaystyle{ P(k)\sim k^{-3} \, }[/math]


中心节点表现出很高的介数中心性，这使得节点之间存在捷径。因此，BA模型的平均路径长度往往很短。该模型的聚集系数也趋于0。


当包括Erdős Rényi随机图模型和一些小世界网络在内的许多模型的直径[math]\displaystyle{ D }[/math]正比于[math]\displaystyle{ log N }[/math]时，BA模型表现为[math]\displaystyle{ D }[/math]~[math]\displaystyle{ loglogN }[/math]（超小世界）。[20] 注意，平均路径长度随N的变化和直径相同。


中介驱动依附 MDA模型

在中介驱动依附 MDA模型中，一个带有[math]\displaystyle{ m }[/math]边的新节点随机选择一个已连接的节点，然后不与那个节点连接，而是随机地与它的[math]\displaystyle{ m }[/math]个相邻节点连接。随机选择已连接节点的概率[math]\displaystyle{ \Pi(i) }[/math] 为

[math]\displaystyle{ \Pi(i) = \frac{k_i} N \frac{ \sum_{j=1}^{k_i} \frac 1 {k_j} }{k_i}. }[/math]


因子 [math]\displaystyle{ \frac{\sum_{j=1}^{k_i}{\frac{1}{k_j}}}{k_i} }[/math]是节点 [math]\displaystyle{ i }[/math]的[math]\displaystyle{ k_i }[/math]个相邻节点的度的调和平均 IHM的逆。大量的数值研究表明，对于[math]\displaystyle{ m\gt 14 }[/math]，IHM的值在大[math]\displaystyle{ N }[/math]极限下会变成常数，这意味着[math]\displaystyle{ \Pi(i) \propto k_i }[/math]。这表明一个节点的连接（度）越高，获得更多连接的机会就更大，因为它们可以通过中介以更多的方式连接到，这本质上体现了富人越富机制的直观思想（或者BA模型优先链接的规则）。因此，可以看出MDA网络以伪装的方式遵循优先链接规则。[21]


然而，当[math]\displaystyle{ m=1 }[/math] 时，它描述了赢者通吃的机制，因为我们可以发现，几乎[math]\displaystyle{ 99\% }[/math] 的节点的度仅为1，而某一个节点的度超级大。当[math]\displaystyle{ m }[/math]的值增加时，超级富人和穷人之间的差距减小；当[math]\displaystyle{ m\gt 14 }[/math]时，从赢者通吃机制转变为富人更富机制。


适应度模型

Caldarelli等人引入了另一个模型，其中关键成分是顶点的性质。[22] 两个顶点[math]\displaystyle{ i,j }[/math]之间的连接概率由连接函数[math]\displaystyle{ f(\eta_i,\eta_j) }[/math] 给出，该函数是网络节点适应性的函数。


节点的度由下式给出[23]

[math]\displaystyle{ k(\eta_i)=N\int_0^\infty f(\eta_i,\eta_j) \rho(\eta_j) \, d\eta_j }[/math]


如果[math]\displaystyle{ k(\eta_i) }[/math]是[math]\displaystyle{ \eta_i }[/math]的可逆递增函数，那么[math]\displaystyle{ P(k) }[/math]的概率分布为

[math]\displaystyle{ P(k)=\rho(\eta(k)) \cdot \eta'(k) }[/math]


因此，如果适应性[math]\displaystyle{ \eta }[/math]是幂律分布，那么节点的度也遵循幂律分布。


不那么直观地，一个快速衰减的概率分布函数 [math]\displaystyle{ \rho(\eta)=e^{-\eta} }[/math] 加上下面形式的连接函数

[math]\displaystyle{ f(\eta_i,\eta_j)=\Theta(\eta_i+\eta_j-Z) }[/math]

其中 [math]\displaystyle{ Z }[/math] 是常数且 [math]\displaystyle{ \Theta }[/math] 是 Heavyside函数，我们同样得到了无标度网络。


该模型已成功地应用于描述国家间贸易，其中GDP作为不同节点 [math]\displaystyle{ i,j }[/math] 的适应性，并且连接函数是如下的形式 [24] [25]

[math]\displaystyle{ \frac{\delta \eta_i\eta_j}{1+ \delta \eta_i\eta_j}. }[/math]

网络分析

社会网络分析

社会网络分析考察了社会实体之间的关系结构。[26]这些实体通常是个人，但也可能是团体、组织、国家、网站、学术出版物。


自20世纪70年代以来，对网络的实证研究在社会科学发挥了核心作用，许多用于研究网络的数学和统计工具最早是在社会学中发展起来的。[27] 在众多的应用中，社会网络分析被用来分析产品创新、新闻和谣言的扩散机制，同时也被用来检测疾病和与健康相关的行为的传播。它也被应用于市场研究，主要用于分析信任在交换关系中的作用以及社会机制在市场定价中的作用。同样，它也可以用于研究政治运动和社会组织的招募问题，以及概念化科学分歧和学术声望。最近，网络分析（及其相近概念流量分析）在军事情报中得到了重要的应用，用于揭露具有层级性和无领导性本质的叛乱者网络。[28][29]在犯罪学中，它也被用来识别犯罪团伙、犯罪活动、共同犯罪中有影响力的角色，预测犯罪活动以及制定相应的政策。[30]


动态网络分析

动态网络分析考察了在复杂的社会技术系统影响下，不同阶级的实体之间关系的转变结构，反映了社会的稳定和变化，如新群体、主题和领导者的出现。[6][7][8][9][31] 动态网络分析的重点是由多种类型的节点（实体）和多种类型的链接组成的元网络。这些实体可以非常多样化，包括人员、组织、主题、资源、任务、事件、地点，甚至是信仰。


动态网络技术是非常有用的一种方法，特别是对于评估网络随时间变化的趋势和变化，识别新兴领导者，以及检查人与思想的共同进化等方面。


生物网络分析

随着近年来公开的生物学数据的爆炸性增长，分子网络分析引起了人们极大的兴趣。这种分析类型与社会网络分析密切相关，但通常更侧重于网络中的局部模式。例如网络模体 network motifs是指网络中过表达的小的子图。在给定网络结构的情况下，网络中节点和连边的属性中的活动模体是相似的过表达模式。生物网络的分析促进了网络医学的发展，网络医学主要是从交互中观察疾病的影响。[32]


链路分析

链路分析是网络分析的一个子集，主要是探索对象之间的联系。例如，作为警方调查的一部分，可以分析嫌疑人和受害人的地址、他们所拨打过的电话号码、他们在一段时间内参与的金融交易，以及这些对象之间的家庭关系。链路分析提供了许多不同类型的对象之间的关键关系和相互联系，而这些在孤立的信息片段中是看不出来的。计算机辅助或全自动计算机链路分析越来越多地被应用在诸多领域，例如银行和保险机构用来进行欺诈检测，电信运营商用来分析电信网络，医疗部门用来分析流行病学和药理学，执法调查，搜索引擎用于相关性评级（反之，垃圾邮件发送者用于垃圾邮件发送，或业务负责人用来优化搜索引擎）以及进行任何有联系的对象之间的分析。


网络鲁棒性

利用渗流理论研究了网络[33] 的结构鲁棒性。当节点的一个临界比例被移除时，网络变得支离破碎。这种现象被称为渗流[34] ，它代表了一种从有序-无序的临界指数的相变类型。


流行病分析

SIR模型是预测全球传染病在感染人群中传播的最著名的算法之一。


易感人群
[math]\displaystyle{ S = \beta\left(\frac 1 N \right) }[/math]

这个公式描述的是人群中每个易感单元的感染“力”，其中 β 代表的是疾病的传播概率。


跟踪人群中易感人数随时间的变化：

[math]\displaystyle{ \Delta S = \beta \times S {1\over N} \, \Delta t }[/math]


从感染到康复
[math]\displaystyle{ \Delta I = \mu I \, \Delta t }[/math]


随着时间的推移，感染人数的波动幅度为：以 [math]\displaystyle{ \mu }[/math] 来表示特定的恢复率，但在平均感染期 [math]\displaystyle{ {1\over \tau} }[/math] 内减为1，感染个体的数量为 [math]\displaystyle{ I }[/math]，以及时间的变化为 [math]\displaystyle{ \Delta t }[/math]。


感染时期

就 SIR 模型而言，被流行病感染的人口数量取决于 [math]\displaystyle{ R_0 }[/math] 的数值，或“被感染个体所感染的平均人数”。

[math]\displaystyle{ R_0 = \beta\tau = {\beta\over\mu} }[/math]


网络连接分析

一些网络搜索排名算法使用基于链接的中心度矩阵，包括（按顺序）Marchiori的 Hyper Search、Google 的 PageRank、Kleinberg 的 HITS 算法、CheiRank 和 TrustRank 算法。在信息科学和传播学中也进行链接分析，以便从网页的结构中理解和提取信息。例如，可以分析政客的网站或博客之间的相互联系。


PageRank

PageRank算法的工作原理是随机选择“节点”或网站，然后以一定的概率“随机跳转”到其他节点。由于存在一些不容易被评估的边缘网站，因此通过随机跳转到这些其他节点，PageRank算法可以完全遍历网络。


每个节点 [math]\displaystyle{ x_i }[/math] 都有一个PageRank，定义为从 [math]\displaystyle{ j }[/math] 连接到 [math]\displaystyle{ i }[/math] 的页面总和乘以1，除以 [math]\displaystyle{ j }[/math] 的出度，再乘以 [math]\displaystyle{ j }[/math] 的“重要性”或PageRank。

[math]\displaystyle{ x_i = \sum_{j\rightarrow i}{1\over N_j}x_j^{(k)} }[/math]


随机跳转

正如上面解释的那样，PageRank通过随机跳转，尝试将PageRank分配给互联网上的每个网站。通过随机跳转可以找到一些在正常的搜索方法（如广度优先搜索和深度优先搜索）中找不到的边缘网站。


在上述公式中，该算法的主要提升是添加了随机跳转，没有这些随机跳转，一些网页的PageRank可能就是0，这样是非常不好的。


第一个为 [math]\displaystyle{ \alpha }[/math]，代表的是随机跳转发生的概率。与此相对的是阻尼因子，即 [math]\displaystyle{ 1 - \alpha }[/math]。

[math]\displaystyle{ R{(p)} = {\alpha\over N} + (1 - \alpha) \sum_{j\rightarrow i} {1\over N_j} x_j^{(k)} }[/math]


从另一个角度来看:

[math]\displaystyle{ R(A) = \sum {R_B\over B_\text{(outlinks)}} + \cdots + {R_n \over n_\text{(outlinks)}} }[/math]


中心性度量

关于图中节点和边的相对重要性的信息可以通过中心性度量来获得，中心性在社会学等学科广泛使用。当网络分析必须回答下面问题时，中心性度量必不可少：“为了确保消息或信息传播到网络中的全部或大部分节点，应该特别关注网络中的哪些节点？”或相反地,“应该控制哪些节点以限制疾病的传播？”。正式确立的中心性度量有度中心性、紧密中心性、中介中心性、本征向量中心性和Katz中心性。网络分析的目标通常决定了要使用的中心性度量的类型。[26]


  • 度中心性是指网络中与某节点相关联的连接（节点）数。
  • 紧密中心性决定了网络中一个节点和其他节点的“紧密”程度，通过计算该节点和网络中其他节点之间的最短路径之和来度量。
  • 中介中心性 通过计算通过某节点到网络中其他节点的流量来确定该节点的相对重要性。这一点可以通过计算网络中所有节点对的路径数中包含感兴趣节点的比例来获得。组中介中心性度量通过一组节点的流量。[35]
  • 本征向量中心性 是度中心性的的一个更加复杂的版本，一个节点的中心性不仅依赖于它的连接数，还取决于这些连接的质量。质量因子由网络邻接矩阵的本征向量决定。
  • Katz 中心性 通过计算某节点与其他可到达节点间最短路径的和来度量。这些路径是有权重的，连接节点与其近邻节点的路径的权重要高于那些与距离其近邻节点较远的节点相连接的路径。

网络内容传播

复杂网络中的内容主要通过两种方式传播：保守传播和非保守传播。[36] 在保守传播中，进入复杂网络的内容总量在传播时保持不变。这个保守传播的模型可以用一个水罐来描述，这个水罐中有一定量的水被注入一系列由管子连接的漏斗中。在这里，水罐代表原始资源，而水则表示被传播的内容。漏斗和连接管分别表示节点和节点之间的连接。当水从一个漏斗流到另一个漏斗时，水立即从先前的漏斗中消失。在非保守传播中，内容的数量在进入和通过复杂网络时发生变化。非保守传播模型可以用一个持续流水的水龙头流过一系列由管子连接的漏斗来表示。在这里，来自原始水源的水量是无限的。而且，即使水已经进入下一个漏斗，任何之前已经接触过水的漏斗也会继续接触水。非保守模型最适合解释大多数传染病的传播。


SIR 模型

1927年， W. O. Kermack 和 A. G. McKendrick 建立了一个仅包含三种人群的固定人口模型，即易感者： [math]\displaystyle{ S(t) }[/math]，被感染者， [math]\displaystyle{ I(t) }[/math]和康复者 [math]\displaystyle{ R(t) }[/math]。该模型中使用的分类可分为三种：

  • [math]\displaystyle{ S(t) }[/math] 用来表示在t时刻尚未感染该疾病或者容易感染该疾病的个体数
  • [math]\displaystyle{ I(t) }[/math] 表示已经感染该疾病并能够将该疾病传播给易感人群的个体数
  • [math]\displaystyle{ R(t) }[/math] 表示感染过疾病但是已经康复的个体数。这部分个体不会再次被感染，也不会将疾病传染给易感人群。


该模型中的流可以这样表示：

[math]\displaystyle{ \mathcal{S} \rightarrow \mathcal{I} \rightarrow \mathcal{R} }[/math]


对于数量固定的群体，有[math]\displaystyle{ N = S(t) + I(t) + R(t) }[/math]， 从而Kermack 和 McKendrick 得到以下方程：

[math]\displaystyle{ \begin{align} \frac{dS}{dt} & = - \beta S I \\[8pt] \frac{dI}{dt} & = \beta S I - \gamma I \\[8pt] \frac{dR}{dt} & = \gamma I \end{align} }[/math]


这些方程的成立有以下的假设：首先，人群中的个体必须被认为具有与其他个体相同的感染该疾病的概率，其比率记为[math]\displaystyle{ \beta }[/math]，该比率被认为是该疾病的接触或感染率。因此，单位时间内一个感染者可以接触并感染[math]\displaystyle{ \beta N }[/math]个其他人，而一个感染者和易感者接触的比例为[math]\displaystyle{ S/N }[/math]。所以单位时间内单个感染者新感染的人数为 [math]\displaystyle{ \beta N (S/N) }[/math]，从而得到新增感染率（易感人群减少率）为 [math]\displaystyle{ \beta N (S/N)I = \beta SI }[/math] （Brauer & Castillo-Chavez, 2001）。对于第二和第三个方程，考虑易感者减少的数量等于感染者增加的数量，但是同时单位时间内会有比率为[math]\displaystyle{ \gamma }[/math]的个体从感染者变为康复者/移除者（其中[math]\displaystyle{ \gamma }[/math]表示平均康复率，或者[math]\displaystyle{ 1/\gamma }[/math]表示平均感染周期）。这些同时发生的过程被认为遵循质量作用定律，这是一个被广泛接受的观点，即群体中两组人群接触的概率正比于两组人群的规模。最后，模型假定感染和康复的速率远远快于出生和死亡的时间尺度，因此这些因素可以被忽略。


更多详细信息请查询流行病模型页面。


主方程法

其中 [math]\displaystyle{ p(k,s,t) }[/math] 是 [math]\displaystyle{ t }[/math]时刻Jxzhou（讨论）（原文中是t+1，我觉得应该是t）Jxzhou（讨论）节点[math]\displaystyle{ s }[/math]的度为[math]\displaystyle{ k }[/math]的概率，[math]\displaystyle{ s }[/math]是该节点添加到网络中的时间步长。使旧节点[math]\displaystyle{ s }[/math]在[math]\displaystyle{ t+1 }[/math]时刻的度为[math]\displaystyle{ k }[/math]的方法只有两种：

  • 节点[math]\displaystyle{ s }[/math] 在[math]\displaystyle{ t }[/math]时刻的度为[math]\displaystyle{ k-1 }[/math]，并且将由概率为[math]\displaystyle{ 1/t }[/math]的新节点连接
  • 在[math]\displaystyle{ t }[/math]时刻的度已经为[math]\displaystyle{ k }[/math]，并且不会被新节点链接。


通过简化模型，可以得到度分布为 [math]\displaystyle{ P(k) = 2^{-k}. }[/math][37]


基于上述生长网络，可以按照以下规则生成流行病模型：每次新添节点并且选择要链接的旧节点时，需要做以下决定：这个新节点是否为感染者。流行病模型的主方程形式为：

[math]\displaystyle{ p_r(k,s,t) = r_t \frac 1 t p_r(k-1,s,t) + \left(1 - \frac 1 t \right) p_r(k,s,t), }[/math]

其中 [math]\displaystyle{ r_t }[/math] 代表感染者 ([math]\displaystyle{ r_t = 1 }[/math]) 或者非感染者 ([math]\displaystyle{ r_t = 0 }[/math])的决定。求解这个主方程，可以得到这样的解： [math]\displaystyle{ \tilde{P}_r(k) = \left(\frac r 2 \right)^k. }[/math][38]

相依网络

相依网络是一个耦合的网络系统，其中一个或多个网络的节点依赖于其他网络中的节点。现代科技的发展增强了这种依赖性。依赖关系可能导致网络之间的相继故障，一个相对较小的故障可能导致系统的灾难性崩溃。网络之间依赖性的重要作用可以通过停电这个例子来展示。最近的一项研究开发了一个框架来研究相互依赖的网络系统中的相继故障。[39][40]

多层网络

多层网络是包含多种关系的网络。已经在多个领域尝试将现实世界系统建模为多维网络，例如社会网络分析、经济学、历史、城市和国际交通、生态学、心理学、医学、生物学、商业、气候学、物理学、计算神经科学、运营管理以及金融。

网络优化

关于寻找某些事情最优解的网络问题属于组合优化的范畴。例如网络流、最短路径问题、运输问题、转运问题、选址问题、匹配问题、分配问题、装箱问题、路由问题、关键路径分析和PERT（计划评审技术）。

参阅

参考文献

  1. ↑ Committee on Network Science for Future Army Applications (2006). Network Science. National Research Council. doi:10.17226/11516. ISBN 978-0309653886. http://www.nap.edu/catalog/11516.html. 
  2. ↑ Dénes Kőnig (1990). Theory of finite and infinite graphs (PDF). Birkhäuser Boston. doi:10.1007/978-1-4684-8971-2. ISBN 978-1-4684-8971-2. https://link.springer.com/content/pdf/10.1007/978-1-4684-8971-2_2.pdf. 
  3. ↑ 3.0 3.1 Lawyer, Glenn (March 2015). "Understanding the spreading power of all nodes in a network". Scientific Reports. 5 (O8665): 8665. arXiv:1405.6707. Bibcode:2015NatSR...5E8665L. doi:10.1038/srep08665. PMC 4345333. PMID 25727453.
  4. ↑ Sikic, Mile; Lancic, Alen; Antulov-Fantulin, Nino; Stefancic, Hrvoje (October 2013). "Epidemic centrality -- is there an underestimated epidemic impact of network peripheral nodes?". European Physical Journal B. 86 (10): 440. arXiv:1110.2558. Bibcode:2013EPJB...86..440S. doi:10.1140/epjb/e2013-31025-5.
  5. ↑ Borgatti, Stephen P. (2005). "Centrality and Network Flow". Social Networks. 27: 55–71. CiteSeerX 10.1.1.387.419. doi:10.1016/j.socnet.2004.11.008.
  6. ↑ 6.0 6.1 Braha, D.; Bar-Yam, Y. (2006). "From Centrality to Temporary Fame: Dynamic Centrality in Complex Networks". Complexity. 12 (2): 59–63. arXiv:physics/0611295. Bibcode:2006Cmplx..12b..59B. doi:10.1002/cplx.20156.
  7. ↑ 7.0 7.1 Hill, S.A.; Braha, D. (2010). "Dynamic Model of Time-Dependent Complex Networks". Physical Review E. 82 (4): 046105. arXiv:0901.4407. Bibcode:2010PhRvE..82d6105H. doi:10.1103/physreve.82.046105. PMID 21230343.
  8. ↑ 8.0 8.1 Gross, T. and Sayama, H. (Eds.). 2009. Adaptive Networks: Theory, Models and Applications. Springer.
  9. ↑ 9.0 9.1 Holme, P. and Saramäki, J. 2013. Temporal Networks. Springer.
  10. ↑ Travençolo, B. A. N.; da F. Costa, L. (2008). "Accessibility in complex networks". Physics Letters A. 373 (1): 89–95. Bibcode:2008PhLA..373...89T. doi:10.1016/j.physleta.2008.10.069.
  11. ↑ Bender, Edward A; Canfield, E.Rodney (May 1978). "The asymptotic number of labeled graphs with given degree sequences". Journal of Combinatorial Theory, Series A. 24 (3): 296–307. doi:10.1016/0097-3165(78)90059-6. ISSN 0097-3165.
  12. ↑ 12.0 12.1 Molloy, Michael; Reed, Bruce (March 1995). "A critical point for random graphs with a given degree sequence". Random Structures & Algorithms (in English). 6 (2–3): 161–180. CiteSeerX 10.1.1.24.6195. doi:10.1002/rsa.3240060204. ISSN 1042-9832.
  13. ↑ 13.0 13.1 Newman, M. E. J.; Strogatz, S. H.; Watts, D. J. (2001-07-24). "Random graphs with arbitrary degree distributions and their applications". Physical Review E. 64 (2): 026118. arXiv:cond-mat/0007235. Bibcode:2001PhRvE..64b6118N. doi:10.1103/PhysRevE.64.026118. PMID 11497662.
  14. ↑ Kryven, Ivan (2017-05-02). "General expression for the component size distribution in infinite configuration networks". Physical Review E. 95 (5): 052303. arXiv:1703.05413. Bibcode:2017PhRvE..95e2303K. doi:10.1103/PhysRevE.95.052303. PMID 28618550.
  15. ↑ Kryven, Ivan (2018-01-01). "Analytic results on the polymerisation random graph model". Journal of Mathematical Chemistry (in English). 56 (1): 140–157. doi:10.1007/s10910-017-0785-1. ISSN 0259-9791.
  16. ↑ Kryven, Ivan (2016-07-27). "Emergence of the giant weak component in directed random graphs with arbitrary degree distributions". Physical Review E. 94 (1): 012315. arXiv:1607.03793. Bibcode:2016PhRvE..94a2315K. doi:10.1103/PhysRevE.94.012315. PMID 27575156.
  17. ↑ Kryven, Ivan (2017-11-02). "Finite connected components in infinite directed and multiplex networks with arbitrary degree distributions". Physical Review E. 96 (5): 052304. arXiv:1709.04283. Bibcode:2017PhRvE..96e2304K. doi:10.1103/PhysRevE.96.052304. PMID 29347790.
  18. ↑ R. Albert; A.-L. Barabási (2002). "Statistical mechanics of complex networks" (PDF). Reviews of Modern Physics. 74 (1): 47–97. arXiv:cond-mat/0106096. Bibcode:2002RvMP...74...47A. CiteSeerX 10.1.1.242.4753. doi:10.1103/RevModPhys.74.47. Archived from the original (PDF) on 2015-08-24.
  19. ↑ Albert-László Barabási & Réka Albert (October 1999). "Emergence of scaling in random networks" (PDF). Science. 286 (5439): 509–512. arXiv:cond-mat/9910332. Bibcode:1999Sci...286..509B. doi:10.1126/science.286.5439.509. PMID 10521342. Archived from the original (PDF) on 2012-04-17.
  20. ↑ Cohen, R.; Havlin, S. (2003). "Scale-free networks are ultrasmall". Phys. Rev. Lett. 90 (5): 058701. arXiv:cond-mat/0205476. Bibcode:2003PhRvL..90e8701C. doi:10.1103/PhysRevLett.90.058701. PMID 12633404.
  21. ↑ Hassan, M. K.; Islam, Liana; Arefinul Haque, Syed (March 2017). "Degree distribution, rank-size distribution, and leadership persistence in mediation-driven attachment networks". Physica A. 469: 23–30. arXiv:1411.3444. Bibcode:2017PhyA..469...23H. doi:10.1016/j.physa.2016.11.001.
  22. ↑ Caldarelli G., A. Capocci, P. De Los Rios, M.A. Muñoz, Physical Review Letters 89, 258702 (2002)
  23. ↑ Servedio V.D.P., G. Caldarelli, P. Buttà, Physical Review E 70, 056126 (2004)
  24. ↑ Garlaschelli D., M I Loffredo Physical Review Letters 93, 188701 (2004)
  25. ↑ Cimini G., T. Squartini, D. Garlaschelli and A. Gabrielli, Scientific Reports 5, 15758 (2015)
  26. ↑ 26.0 26.1 Wasserman, Stanley and Katherine Faust. 1994. Social Network Analysis: Methods and Applications. Cambridge: Cambridge University Press.
  27. ↑ Newman, M.E.J. Networks: An Introduction. Oxford University Press. 2010
  28. ↑ "Toward a Complex Adaptive Intelligence Community The Wiki and the Blog". D. Calvin Andrus. cia.gov. Retrieved 25 August 2012.
  29. ↑ "Network analysis of terrorist networks". Archived from the original on 2012-11-23. Retrieved 2011-12-12.
  30. ↑ PhD, Martin Bouchard; PhD, Aili Malm (2016-11-02). "Social Network Analysis and Its Contribution to Research on Crime and Criminal Justice" (in English). doi:10.1093/oxfordhb/9780199935383.013.21. {{cite journal}}: Cite journal requires |journal= (help)
  31. ↑ Xanthos, Aris, Pante, Isaac, Rochat, Yannick, Grandjean, Martin (2016). Visualising the Dynamics of Character Networks. In Digital Humanities 2016: Jagiellonian University & Pedagogical University, Kraków, pp. 417–419.
  32. ↑ Barabási, A. L.; Gulbahce, N.; Loscalzo, J. (2011). "Network medicine: a network-based approach to human disease". Nature Reviews Genetics. 12 (1): 56–68. doi:10.1038/nrg2918. PMC 3140052. PMID 21164525.
  33. ↑ R. Cohen; S. Havlin (2010). Complex Networks: Structure, Robustness and Function. Cambridge University Press. http://havlin.biu.ac.il/Shlomo%20Havlin%20books_com_net.php. 
  34. ↑ A. Bunde; S. Havlin (1996). Fractals and Disordered Systems. Springer. http://havlin.biu.ac.il/Shlomo%20Havlin%20books_fds.php. 
  35. ↑ Puzis, R.; Yagil, D.; Elovici, Y.; Braha, D. (2009). "Collaborative attack on Internet users' anonymity" (PDF). Internet Research. 19: 1. CiteSeerX 10.1.1.219.3949. doi:10.1108/10662240910927821. Archived from the original (PDF) on 2013-12-07. Retrieved 2015-02-08.
  36. ↑ Newman, M., Barabási, A.-L., Watts, D.J. [eds.] (2006) The Structure and Dynamics of Networks. Princeton, N.J.: Princeton University Press.
  37. ↑ Dorogovtsev, S N; Mendes, J F F (2003). Evolution of Networks: From Biological Nets to the Internet and WWW. New York, NY, USA: Oxford University Press, Inc.. ISBN 978-0198515906. 
  38. ↑ Cotacallapa, M; Hase, M O (2016). "Epidemics in networks: a master equation approach". Journal of Physics A. 49 (6): 065001. arXiv:1604.01049. Bibcode:2016JPhA...49f5001C. doi:10.1088/1751-8113/49/6/065001.
  39. ↑ S. V. Buldyrev; R. Parshani; G. Paul; H. E. Stanley; S. Havlin (2010). "Catastrophic cascade of failures in interdependent networks". Nature. 464 (7291): 1025–28. arXiv:0907.1182. Bibcode:2010Natur.464.1025B. doi:10.1038/nature08932. PMID 20393559.
  40. ↑ Gao, Jianxi; Buldyrev, Sergey V.; Havlin, Shlomo; Stanley, H. Eugene (2011). "Robustness of a Network of Networks". Phys. Rev. Lett. 107 (19): 195701. arXiv:1010.5829. Bibcode:2011PhRvL.107s5701G. doi:10.1103/PhysRevLett.107.195701. PMID 22181627.

进一步阅读


编者推荐

书籍推荐

《网络科学引论》封面
作者Newman凭借在计算机、信息论、物理等相关学科的深入研究和丰富经验，系统地分析和论述了网络作为一门科学理论如何应用在现实生活中的方方面面。全书分为5部分，讨论了目前科学研究中的网络类型和用以确定其结构的各种技术，介绍了研究网络的基本数学理论及用以量化网络结构的各类测度与参数，描述了有效分析网络数据的计算机算法，以及有助于预测网络系统行为并理解其生成和演化过程的网络结构数学模型，最后给出了网络上的一些动力学过程，如社会网络中的疾病传染或计算机网络上的搜索过程。


《巴拉巴西网络科学》封面
《巴拉巴西网络科学》列举了很多生活中的案例，深入浅出，全面而系统地绘制出一幅网络科学领域的知识地图。关于网络，你想知道的一切都能在这本书中找到。
全球复杂网络研究权威、“无标度网络”奠基人艾伯特-拉斯洛·巴拉巴西花费5年心血，用丰富的案例和研究成果，结合大量图表和参考文献，将网络科学的专业知识融汇成10大模块，以大众视角讲透网络科学；中国科学院计算技术研究所研究员、网络科学和社会计算专家沈华伟、普林斯顿大学博士后黄俊铭担纲翻译，最大程度还原原著。作为一本专业教材，《巴拉巴西网络科学》是网络科学领域研究者、教师、学生的必备佳作；除此之外，本书文笔流畅、通俗易懂，将网络科学的理论与日常生活联系起来，为普通大众了解当今的互联世界提供了一个通道。


《网络科学导论》由汪小帆，李翔，陈关荣联袂编著，致力于系统地介绍网络科学的基本概念、思想和方法，使得具有高等数学基础的读者都能够看懂，并具备把网络科学方法用于实际网络分析的能力。为此，本书没有过多地陷入数学和物理推导，而是更为关注网络科学的思维习惯和研究方式。


文章推荐

网络科学日新月异，在新的一年中，有哪些最新的研究方向？曾获网络科学大会ER奖的加州大学洛杉矶分校数学教授Mason A. Porter，近期在 arxiv.org 提交了一篇综述论文 Nonlinearity + Networks: A 2020 Vision，指出了未来复杂网络研究的四个热点，分别是：
  1. 时序网络 temporal networks
  2. 网络上的动力学过程 dynamical processes on network
  3. 自适应网络 adaptive network
  4. 高阶网络 high order network


集智文章推荐

复杂性科学的兴起离不开众多科研机构的助力，这些科研机构整合不同领域里的学术资源，孕育了大批的复杂性科学的人才。当然，除了著名的圣塔菲研究所，还有很多其他的机构，我们对这些机构做了一个梳理，供大家参考，有一个全面的认识。本文主要介绍北美一些有代表性的复杂性科学研究机构。


网络科学入门》全文概念地图
本文围绕4个问题展开，分别是:
  1. 什么是幂律分布
  2. 什么是无标度网络
  3. 如何产生幂律分布
  4. 如何估计和判断幂律分布




课程推荐

本课程中，邀请了10位全国最顶尖的复杂科学专家为您全面系统讲解网络科学，帮助大家完成从散点思维到网络思维，直至网络科学思维的跃升。
巴拉巴西网络科学


本课程是对复杂性科学的一个概述，包含10个章节，每节都会涵盖复杂系统的一个主要概念。


本课程中，将详细介绍复杂网络的四个基本模型：规则网、随机图、小世界网络、Scale-Free 网络。


本课程主要讲解图卷积神经网络（GCN），GCN是针对不规则图（图像可以看作是规则的二维网格）的一种卷积神经网络的技术，可以用来进行图上信号的识别和预测。

本中文词条由思无涯咿呀咿呀和jxzhou 参与编译，苏格兰审校，乐多多编辑，欢迎在讨论页面留言。


本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

取自“https://wiki.swarma.org/index.php?title=网络科学&oldid=28264”