周期点
在数学中,特别是在迭代函数和动力系统的研究领域中,函数的周期点是系统在一定次数的函数迭代或一定时间后返回的点。这里的迭代次数叫做周期。周期为1的周期点被称为不动点。
迭代函数
给定一个从集合[math]\displaystyle{ X }[/math]到自身的映射[math]\displaystyle{ f }[/math],
[math]\displaystyle{ f: X \to X, }[/math]
[math]\displaystyle{ X }[/math]中的点[math]\displaystyle{ x }[/math]称为周期点,如果存在一个[math]\displaystyle{ n }[/math]使
[math]\displaystyle{ \ f_n(x) = x }[/math]
其中[math]\displaystyle{ f_n }[/math]为[math]\displaystyle{ f }[/math]的第[math]\displaystyle{ n }[/math]次迭代。满足上述条件的最小正整数[math]\displaystyle{ n }[/math]称为点[math]\displaystyle{ x }[/math]的素数周期prime period或最小周期。如果[math]\displaystyle{ X }[/math]中的每一个点都是周期为[math]\displaystyle{ n }[/math]的周期点,那么[math]\displaystyle{ f }[/math]有周期性,周期为[math]\displaystyle{ n }[/math](这不能和周期函数的概念混淆)。
如果存在不同的[math]\displaystyle{ n }[/math]和[math]\displaystyle{ m }[/math]使:[math]\displaystyle{ f_n(x) = f_m(x) }[/math]
那么[math]\displaystyle{ x }[/math]称为前周期点 preperiodic point。所有周期点都是前周期点。
如果[math]\displaystyle{ x }[/math]是微分流形的微分同胚,则定义了导数[math]\displaystyle{ f_n^\prime }[/math],如果:[math]\displaystyle{ |f_n^\prime|\ne 1, }[/math],那么[math]\displaystyle{ f }[/math]是双曲周期点;
如果:[math]\displaystyle{ |f_n^\prime|\lt 1, }[/math],则称周期点[math]\displaystyle{ f }[/math]为吸引子;
如果:[math]\displaystyle{ |f_n^\prime|\gt 1. }[/math],则称周期点[math]\displaystyle{ f }[/math]为排斥子。
如果周期点或不动点的稳定流形的维数为零,则称其为源点;如果不稳定流形的维数为零,则称其为汇点;如果稳定流形和不稳定流形都有非零维数,则称其为鞍点。
示例
周期为1的点也叫做不动点。
逻辑斯谛克映射函数表达式:
- [math]\displaystyle{ x_{t+1}=rx_t(1-x_t), \qquad 0 \leq x_t \leq 1, \qquad 0 \leq r \leq 4 }[/math]
参数[math]\displaystyle{ r }[/math]随着取值的不同,呈现周期性。
- 对于介于0到1之间的[math]\displaystyle{ r }[/math],0是唯一的周期点,周期为1(给出了吸引所有轨道的序列0,0,0,... );
- 对于介于1到3之间的[math]\displaystyle{ r }[/math],值0仍然是周期性的,但不是吸引子,而该值是周期1的周期吸引子;
- 当[math]\displaystyle{ r }[/math]大于3但小于1时,存在一对周期2的点,它们共同构成一个吸引序列,非吸引周期1点为0;
- 当参数[math]\displaystyle{ r }[/math]的值上升到4时,会出现周期为正的一组周期点;
- 对于[math]\displaystyle{ r }[/math]的某些值,这些重复序列中的一个被吸引,而对于其他值,则没有一个被吸引(几乎所有的轨道都是混乱的)。
动力系统
给定一个连续时间的动力系统[math]\displaystyle{ (R,X,Φ) }[/math],其中[math]\displaystyle{ X }[/math]为相空间,[math]\displaystyle{ Φ }[/math]为状态转移函数,
[math]\displaystyle{ \Phi: \mathbb{R} \times X \to X }[/math]
如果存在 [math]\displaystyle{ t \gt =0 }[/math],则[math]\displaystyle{ X }[/math]中的点[math]\displaystyle{ x }[/math]称为周期为[math]\displaystyle{ t }[/math]的周期。使得:
[math]\displaystyle{ \Phi(t, x) = x\, }[/math]
具有此性质的最小正数[math]\displaystyle{ t }[/math]称为点[math]\displaystyle{ x }[/math]的最小周期。
性质
- 给定一个周期为[math]\displaystyle{ “p” }[/math]的周期点[math]\displaystyle{ “x” }[/math],则对于[math]\displaystyle{ t∈R }[/math],[math]\displaystyle{ \Phi(t,x) = \Phi(t+p,x) }[/math]
- 给定周期点“x”,则在轨道 [math]\displaystyle{ \gamma_x }[/math]上的所有点都具有相同的素数周期prime period。
请参见
- 极限环Limit cycle
- 极限集合Limit set
- 稳定集 Stable set
- Sharkovsky定理Sharkovsky's theorem
- 驻点 Stationary point
- 复杂二次映射的周期点Periodic points of complex quadratic mappings
编者推荐
集智课程
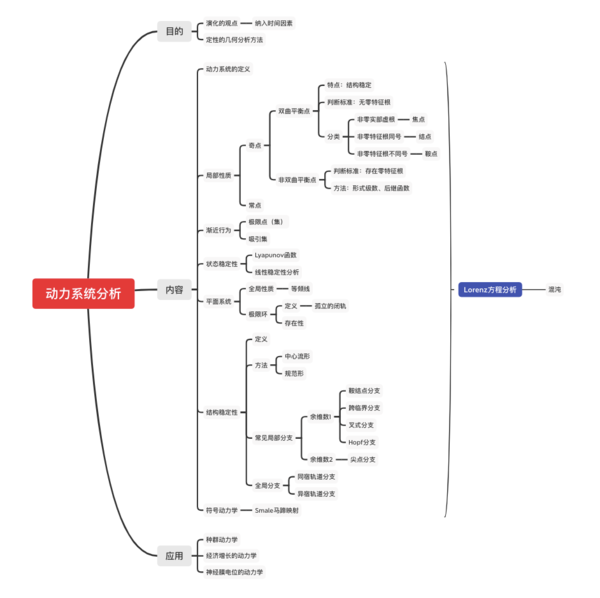
动力系统分析
复杂系统研究中,自顶向下的动力学分析方法是探索复杂性的重要方法。本课程主要讲授连续和离散动力系统的定态、极限环及其稳定性分析、动力学系统的结构稳定性和常见的分支类型以及分析方法,混沌概念等。
本课程是系统科学专业的学位基础课,是系统科学博士研究生培养的基础课程。主要培养硕士、博士研究生从动力学演化角度观察世界的能力,并可以分析具体的动力学系统,能够分析研究对象中随时间变化的状态变量以及变量之间的关系,建立动力学方程并进行定性和定量的分析,是非线性系统控制、控制理论、复杂系统建模与分析以及系统生物学等专业课的理论基础,应用领域涉及国防、科技、经济、工业和农业的各个方面。
圣塔菲课程:Introduction to Dynamical Systems and Chaos
本课程主要介绍动力学系统和混沌系统,您将学到蝴蝶效应(butterfly effect)、奇异吸引子(attractors)等基本概念,以及如何应用于您感兴趣的领域。课程主题涉及相空间(phase space),分叉(bifurcations),混沌(chaos),蝴蝶效应(butterfly effect),奇怪吸引子(strange attractors)和模式生成(pattern formation)。
该课程将重点研究与复杂系统紧密联系的动力学系统:
- 动力系统会发生分叉,其中系统参数(例如温度或渔业中的收获率)的微小变化会导致系统行为的质变。
- 确定性动力学系统也存在随机性。这种特性被称为敏感依赖性(sensitive dependence)或蝴蝶效应,这严重限制了我们预测某些现象的能力。
- 随机行为存在一定规律。具有蝴蝶效应的非周期性系统可以具有稳定的平均特性。因此,即使无法预测系统的详细信息,也可以预测系统的平均或统计属性。
- 复杂行为可能源于简单规则,简单的动力学系统不一定会导致简单的结果。我们将看到简单规则会导致惊人复杂的模式和结构。
相关文章
本中文词条由舒寒、思无涯咿呀咿呀翻译,思无涯咿呀咿呀审校,思无涯咿呀咿呀编辑,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。