囚徒困境

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
跳到导航 跳到搜索
囚徒困境支付矩阵

囚徒困境 prisoner's dilemma是博弈论分析博弈的一个代表性例子，它揭示了为什么两个完全理性的个体可能不会合作，即使这样做符合他们的最大利益。它最初是由梅里尔·弗勒德 Merrill Flood和 梅文·加舍尔 Melvin Dresher于1950年在兰德公司工作时构建的。阿尔伯特.W.塔克 Albert W. Tucker将这种博弈以监禁刑罚奖励的方式正式化，并将其命名为囚徒困境 [1]，具体阐述如下：


一个犯罪团伙的两名成员被捕入狱。每个囚犯都被单独监禁，与他人无法沟通。检察官缺乏足够的证据来对这两个人定罪，但有足够的证据以较低的罪名定罪。同时，检察官向每个犯人提供了一个交易。每个囚犯都有机会出卖对方，证明对方犯下的罪行，或者他们可以合作，保持沉默。可能的结果有:

  • 如果A和B都背叛了对方，他们都会在监狱服刑两年。
  • 如果A背叛了B但B保持沉默，A会被无罪释放而B会服刑三年。
  • 如果A保持沉默但B背叛了A，A会服刑三年而B会无罪释放。
  • 如果A和B都保持沉默，他们就只用服刑一年（以较低的罪名）。


这意味着，囚犯除了监禁刑罚之外，没有机会奖励或惩罚他们的同伴，他们的决定也不会影响他们未来的声誉。因为背叛一个同伴比与他们合作能得到更大的回报，所以所有纯粹理性的、自私自利的囚犯都会背叛对方，这意味着，对于两个纯粹理性的囚犯来说，唯一可能的结果就是他们相互背叛。[2]实际上，尽管“理性的”自利行为的简单模型已经预测到了这一点，但人类在这种和类似的博弈中仍然表现出对合作行为的系统性偏差 systemic bias。[3][4][5][6]自从在兰德公司首次进行这项测试以来，人们就已经知道了这种对合作的偏见; 参与测试的秘书们相互信任，为了最好的共同的目标而努力。[7]囚徒困境成为大量实验研究的焦点。[8] [9]


一个扩展的重复版本的博弈由此衍生出来。在这个版本中，经典博弈会在在同一组囚犯之间重复进行，他们不断有机会为了之前的决定对其他囚犯进行惩罚。如果参与者知道博弈的次数，那么(通过逆向归纳法 backward induction )两个经典的理性的玩家就会因为和在单次博弈中相同的原因反复背叛对方。在无限次或未知次数的博弈中，没有固定的最优策略，因而，举办囚徒困境竞赛来竞争和检验这种情况下的算法。[10]


囚徒困境博弈可以作为许多现实中涉及合作行为的模型。在非正式用法中，“囚徒困境”一词可适用于不严格符合经典或重复博弈的形式标准的情况: 例如，两个实体可以从合作中获得巨大利益或者会因为合作失败而遭受损失，但发现协调他们的活动很困难或者代价昂贵（并非是不可能的）。


囚徒困境的策略

两名囚犯被分开关押在各自的房间里，不能相互交流。


正常的博弈如下:

A\B 犯人B保持沉默
(合作)		 犯人B背叛
(背叛)
犯人A保持沉默
(合作) 		每人服刑1年 囚犯 A: 3年
囚犯 B: 无罪释放
犯人A背叛
(背叛) 		囚犯 A: 获释
囚犯 B: 3年		 每人服刑2年


假设两个囚犯都了解博弈的本质，对彼此不忠诚，且在博弈之外没有机会得到报复或奖励。那么不管对方怎么决定，每个犯人背叛对方都会得到更高的奖励(“叛变”)。推理涉及一个进退两难的论点:B 要么合作，要么叛变。如果B合作，A 应该叛变，因为得到释放总比服刑1年好。如果 B叛变，A也应该叛变，因为服刑2年总比服刑3年好。所以不管怎样，A都应该叛变。并行推理表明B应该选择叛变。


因为不管对方的选择如何，背叛总是比合作带来更好的回报，所以这是一个占优策略 dominant strategy。相互背叛是博弈中唯一的强纳什均衡点（即每个参与者单方面的改变策略只能使自己的情况变糟)。因此，困境在于，虽然相互合作比相互背叛产生更好的结果，但它却不是理性的结果，因为从自我利益的角度来看，合作的选择是非理性的。


广泛形态

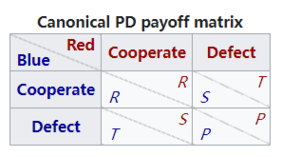
传统囚徒困境的结构可以从其最初的囚徒环境中概括出来。假设两个玩家用红色和蓝色表示，并且每个玩家选择“合作”或“背叛”。


如果两个玩家合作，他们都会因为合作而获得奖励R。如果两个参与人都叛变，他们都会受到惩罚P。 如果蓝方叛变而红方合作，那么蓝方得到诱惑回报T，而红方受到“上当受骗者”损失S。同样地，如果蓝方合作而红方叛变，那么蓝方得到上当受骗者的损失S，而红方得到诱惑支付T。


这可以用标准形式的博弈来表示:


正则 PD 支付矩阵


要成为强意义下的囚徒困境博弈，收益必须满足以下条件:


[math]\displaystyle{ T \gt R \gt P \gt S }[/math]


回报关系[math]\displaystyle{ R \gt P }[/math]意味着相互合作优于相互背叛，然而回报关系[math]\displaystyle{ T \gt R }[/math]和[math]\displaystyle{ P \gt S }[/math]也意味着相互背叛是双方的占优策略。


特例：捐赠博弈

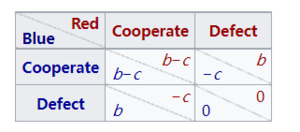
捐赠博弈[11]是囚徒困境的一种形式，在这种博弈中，合作相当于以b > c条件下的个人成本c为另一方提供一个收益b，而叛变意味着什么也不提供。收益矩阵如下：


捐赠博弈收益矩阵


请注意[math]\displaystyle{ 2R\gt T+S }[/math]（即[math]\displaystyle{ 2(b-c)\gt b-c }[/math]）这使得捐赠博弈成为一个重复博弈(见下一节)。


捐赠博弈可能适用于市场。假设种植者X 种橘子，种植者Y 种苹果。苹果对橙子种植者 X 的边际效用 marginal utility是b，“b”比橙子的边际效用c高，因为X有橙子剩余而没有苹果。同样地，对于苹果种植者Y来说，橙子的边际效用是b，而苹果的边际效用是c。 如果X和Y签约交换一个苹果和一个橙子，并且每个人都完成了交易，那么每个人都会得到b-c的收益。如果一方违约没有按照承诺交货，那么这个违约者将得到b的收益，而合作者将失去c的收益。 如果两者都违约，那么谁也不会得到或失去任何东西。


重复囚徒困境

如果两个参与者连续进行多次囚徒困境博弈，他们记住对手先前的行动并相应地改变策略，这种博弈被称为重复囚徒困境。


除了上面的一般形式之外，重复版本还要求[math]\displaystyle{ 2R \gt T + S }[/math]，防止交替合作和背叛比相互合作有更大的回报。


重复囚徒困境博弈是人类合作与信任的理论基础。假设博弈可以为两个需要信任的人之间的交易建模，那么群体中的合作行为也可以由多个参与者重复的博弈模型来建模。因此，这些年来，它吸引了许多学者。1975年，葛夫曼 Grofman和普尔 Pool估计专门撰写有关该领域的学术文章超过2000篇。重复囚徒困境也被称为“和平-战争博弈”。[12]


如果这个游戏正好玩了N次，并且两个玩家都知道这一点，那么在所有回合中最佳的策略就是叛变。唯一可能的纳什均衡点就是永远叛变。证明是通过归纳法证出来的: 不妨假设一个人在最后一回合叛变，因为对手之后没有机会反击。因此，双方都会在最后一个回合叛变。所以玩家同样也会在倒数第二回合时叛变，因为无论采取什么策略，对手都会在倒数第一回合叛变，依此类推。如果博弈次数未知但次数有限的情况也同样如此。


与标准的囚徒困境不同，在重复囚徒困境中，叛变策略是严重违反直觉的，以至于不能很好地预测人类玩家的行为。然而，在标准的经济理论中，这是唯一正确的答案。具有固定次数 N的重复囚徒困境中的超理性 superrational策略是与超理性对手进行合作，在N很大的限制下，实验结果的策略与超理性结果的策略一致，而不是博弈论的理性结果。


为了使合作在博弈论的理性参与者之间出现，参与者必须不知道回合总数N。在这种情况下，“总是叛变”可能不再是一个严格占优策略，而只是一个纳什均衡。罗伯特·奥曼 Robert Aumann在1959年的一篇论文中表明，理性参与者在无限多次的博弈中通过反复互动可以维持合作的结果。


根据《美国经济评论》于2019年进行的一项实验研究，该实验中通过完美的监控测试了现实中被用在重复囚徒困境情况下的策略，监测选择的策略总是背叛，针锋相对的和 冷酷触发策略 Grim trigger。受试者选择的策略取决于博弈的参数。[13]


重复囚徒困境下的策略

罗伯特·阿克塞尔罗德 Robert Axelrod在他的著作《合作的进化 The Evolution of Cooperation》(1984)中激起了人们对重复囚徒困境(IPD)的兴趣。在这篇文章中，他报道了自己组织的固定N次囚徒困境的比赛，参与者必须一次又一次地选择他们的共同策略，并且要记住他们之前的遭遇。Axelrod邀请世界各地的学术界同仁设计计算机策略来参加IPD锦标赛。输入的程序在算法复杂性、最初敌意、宽恕能力等方面有很大差异。


Axelrod发现，当这些遭遇长时间在许多玩家身上重复发生时，每个玩家都有不同的策略，从长远来看，贪婪策略往往表现得非常糟糕，而更加利他的策略表现得更好，这完全是根据自身利益来判断的。他利用这一结果揭示了通过自然选择，从最初纯粹自私行为向利他行为进化的可能机制。


最终获胜的决定性策略是针锋相对策略，这是阿纳托尔·拉波波特 Anatol Rapoport开发并参加比赛的策略。这是所有参赛程序中最简单的一个，只有四行 BASIC 语言，并且赢得了比赛。策略很简单，就是在游戏的第一次重复中进行合作; 在此之后，玩家将执行做他的对手在前一步中所做的事情。根据具体情况，一个稍微好一点的策略可以是“带着宽恕之心针锋相对”。当对手叛变时，在下一次博弈中，玩家有时还是会合作，但概率很小(大约1-5%)。这允许博弈偶尔能从陷入叛变循环中恢复过来。确切的概率取决于对手的安排。


通过分析得分最高的战略，Axelrod阐述了战略成功的几个必要条件。


  • 友好:最重要的条件是策略必须是好的，也就是说，它不会在对手之前叛变(这有时被称为“乐观”算法)。几乎所有得分最高的策略都是友好的; 因此，一个纯粹的自私策略不会为了纯粹自身的利益而“欺骗”对手。
  • 报复:然而，阿克塞尔罗德认为，成功的战略决不能是盲目的乐观主义。它有时必须进行报复。非报复策略的一个例子就是永远合作。这是一个非常糟糕的选择，因为“肮脏”的策略会无情地利用这些玩家。
  • 宽容: 成功的策略也必须是宽容的。虽然玩家会报复，但如果对手不继续叛变，他们将再次回到合作的状态。这阻止了长时间的报复和反报复，最大限度地提高积分。
  • 不嫉妒: 最后一个品质是不嫉妒，不强求比对手得分更多。


对于一次性的囚徒困境博弈，最优(点数最大化)策略就是简单的叛变; 正如上面所说，无论对手的构成如何，这都是正确的。然而，在重复囚徒困境博弈中，最优策略取决于可能的对手的策略，以及他们对叛变和合作的反应。例如，考虑一个群体，其中每个人每次都会叛变，只有一个人遵循针锋相对的策略。那个人就会由于第一回合的失利而处于轻微的不利地位。在这样一个群体中，个体的最佳策略是每次都叛变。在一定比例的总是选择背叛的玩家和其余组成选择针锋相对策略的玩家的人群中，个人的最佳策略取决于这一比例和博弈的次数。


在所谓的巴甫洛夫策略 Pavlov strategy中，去输存赢 win-stay, lose-switch，面对一次合作失败，玩家将在下一次变换策略。[14]在某些情况下，巴甫洛夫通过使用类似策略给与合作者优惠待遇打败了其他所有策略。


得出最佳策略通常有两种方法:

  • 贝叶斯纳什均衡：如果可以确定对立策略的统计分布（例如，50%针锋相对，50%总是合作），那么，可以通过分析得出最佳的反策略（例如2003年的研究[15]讨论这一概念以及它是否可以应用于实际经济或战略情况。）


  • 蒙特卡罗方法已经对种群进行了模拟，分数低的个体死亡，分数高的个体繁殖（遗传算法 genetic algorithm用于寻找一个最佳策略）。最终群体中的算法组合通常取决于初始总体的组合。引入突变（繁殖过程中的随机变异）可以减少对初始种群的依赖性。使用这种系统进行经验性实验往往会为针锋相对的玩家带来麻烦（见Chess 1988），但是没有分析证据表明这种情况会一直发生。[16]


尽管针锋相对被认为是最有力的基本策略，来自英格兰南安普敦大学的一个团队在20周年的重复囚徒困境竞赛中提出了一个新策略，这个策略被证明比针锋相对更为成功。这种策略依赖于程序之间的串通，以获得单个程序的最高分数。这所大学提交了60个程序，这些程序的设计目的是在比赛开始时通过一系列的5到10个动作来互相认识。[17]一旦认识建立，一个程序总是合作，另一个程序总是叛变，保证叛变者得到最多的分数。如果这个程序意识到它正在和一个非南安普顿的球员比赛，它会不断地叛变，试图最小化与之竞争的程序的得分。因此，2004年囚徒困境锦标赛的结果显示了南安普敦大学战略位居前三名，尽管它比冷酷战略赢得更少，输的更多。(在囚徒困境锦标赛中，比赛的目的不是“赢”比赛——这一点频繁叛变很容易实现)。此外，即使没有软件策略之间的暗中串通(南安普顿队利用了这一点) ，针锋相对并不总是任何特定锦标赛的绝对赢家; 更准确地说，它是在一系列锦标赛中的长期结果超过了它的竞争对手。(在任何一个事件中，一个给定的策略可以比针锋相对稍微更好地适应竞争，但是针锋相对更稳健)。这同样适用于带有宽恕变量的针锋相对，和其他最佳策略: 在任何特定的一天，他们可能不会“赢得”一个特定的混合反战略。另一种方法是使用达尔文 Darwinian的 ESS模拟 ESS simulation。在这样的模拟中，针锋相对几乎总是占主导地位，尽管讨厌的策略会在人群中漂移，因为使用针锋相对策略的人群可以通过非报复性的好策略进行渗透，这反过来使他们容易成为讨厌策略的猎物。理查德·道金斯 Richard Dawkins指出，在这里，没有静态的混合策略会形成一个稳定的平衡，系统将始终在边界之间振荡。这种策略最终在比赛中获得了前三名的成绩，或者是接近垫底的成绩。


这种策略利用了这样一个事实，即在这场特殊的比赛中允许多个参赛项目，并且团队的表现由得分最高的项目来衡量(这意味着使用自我牺牲的项目是一种分数最大化的形式)。在一个只能控制一个玩家的比赛中，针锋相对当然是一个更好的策略。由于这一新规则的存在，与阿克塞尔罗德的具有深远影响的竞赛相比，这种竞赛在分析单个主体策略时也就没有什么理论意义。然而，它为在分析多主体框架下，特别是在存在干扰的情况下，如何实现协作策略提供了基础。事实上，早在这场新规则锦标赛开始之前，道金斯就在他的《自私的基因》一书中指出，如果允许多次参赛，这种策略就有可能获胜，但他说，如果提交这种策略的话，阿克塞尔罗德很可能不会允许。因为它依赖于规避囚徒困境的规则，即两个参与者之间不允许交流，南安普顿的项目可以说在开场的“十步舞”中就是这样做以认识对方的; 这只是强调了交流在改变游戏平衡方面的价值。


随机重复囚徒困境

在随机重复囚徒困境博弈中，策略由“合作概率”来确定。[18]在玩家X和玩家Y之间的遭遇中，X的策略由一组与Y合作的概率P确定，P是他们之前遭遇的结果的函数，或者是其中的一些子集。如果P只是它们最近遇到次数 n的函数，那么它被称为“记忆-n”策略。我们可以由四个联合概率指定一个记忆-1策略: [math]\displaystyle{ P=\{P_{cc},P_{cd},P_{dc},P_{dd}\} }[/math]，其中[math]\displaystyle{ P_{ab} }[/math]是在当前遭遇中基于先前联合的概率。如果每个概率都是1或0，这种策略称为确定性策略。确定性策略的一个例子是针锋相对策略，写成 p {1,0,1,0} ，其中 x 的反应和 y 在前一次遭遇中的反应一样。另一种是胜-保持-败-转换策略，它被写成 p {1,0,0,1} ，在这种策略中，如果 x 获得胜利(即:cc 或 dc)，x会做出与上一次遭遇一样的反应 ，但如果失败，x会改变策略(即cd 或 dd)。研究表明，对于任何一种记忆-n 策略，存在一个相应的记忆-1策略，这个策略给出相同的统计结果，因此只需要考虑记忆-1策略。[18]


如果我们将P定义为X的上述4元策略向量，并将[math]\displaystyle{ Q=\{Q_{cc},Q_{cd},Q_{dc},Q_{dd}\} }[/math]定义为Y的4元策略向量，则对于X可以定义一个转移矩阵M，其第ij项是X和Y之间特定相遇的结果为j的概率，给定i，其中i和j是cc、cd、dc或dd 四个结果索引中的一个。例如，从X的角度来看，如果给定cd，那么这次的结果是cd的概率等于[math]\displaystyle{ M_{cd,cd}=P_{cd}(1-Q_{dc}) }[/math]。(Q的指标是 从Y的角度: X的cd结果是Y的dc结果)在这些定义下，重复的囚徒困境被定义为一个随机过程，M是一个随机矩阵，允许应用所有的随机过程理论。[18]


随机理论的一个结果是，矩阵M存在一个平稳向量v使得[math]\displaystyle{ v\cdot M=v }[/math]成立。一般地，我们可以指定v是标准化的，因此它的4个组成部分之和为1。现在可以将 和 的均衡收益指定为“和”，从而可以比较两种策略“P”和“Q”的长期收益.第ij项[math]\displaystyle{ M^n }[/math]给出了X和Y相遇的结果的概率为j，给定前面相遇n步的概率是i。当n趋于无穷时，M收敛于一个具有固定值的矩阵，并且j趋向一个长期概率，与i独立。换句话说， [math]\displaystyle{ M^\infty }[/math]的行将是相同的，从而给出了重复囚徒困境的长期均衡结果概率，而不需要明确地计算大量的相互作用。可以看出，v是[math]\displaystyle{ M^n }[/math]特别是[math]\displaystyle{ M^\infty }[/math], 的平稳向量，因此[math]\displaystyle{ M^\infty }[/math]的每一行都等于v。因此平稳向量指定了X的均衡结果概率。定义[math]\displaystyle{ S_x=\{R,S,T,P\} }[/math]和[math]\displaystyle{ S_y=\{R,T,S,P\} }[/math]作为{cc,cd,dc,dd}结果的短期收益向量(从X的角度来看) ，现在可以将X和Y的均衡收益指定为[math]\displaystyle{ s_x=v\cdot S_x }[/math]和[math]\displaystyle{ s_y=v\cdot S_y }[/math]，使得P、Q两种策略的长期收益可以比较。


零决定策略

维恩图 Venn diagram中讨论了重复囚徒困境(IPD)中零决定策略(ZD)、合作策略和背叛策略之间的关系。合作策略总是与其他合作策略相互配合，而背叛策略总是与其他背叛策略相抵触。这两种策略都包都含在强选择下稳健的策略子集，这意味着当它们驻留在一个种群中时，没有选择其他的记忆-1策略来入侵此策略。只有合作策略包含在始终稳健的策略子集，意味着无论选择强项还是弱项，都不会选择其他任何记忆-1策略来入侵和替换此策略。零决定策略和良好的合作策略之间的交集是一组宽松的零决定策略。勒索策略是零决定策略和非稳健背叛策略的交集。针锋相对是合作、背叛和零决定策略的交集。


2012年，威廉·H·普莱斯 William H. Press和弗里曼·戴森 Freeman Dyson针对随机重复囚徒困境提出了一类新的策略，称为“零决定”策略。[18]X和Y之间的长期收益可以表示为一个矩阵的决定因素，它是两个策略和短期收益向量的函数: [math]\displaystyle{ s_x=D(P,Q,S_x) }[/math]和[math]\displaystyle{ s_y=D(P,Q,S_y) }[/math]，不涉及平稳向量v。 由于行列式函数[math]\displaystyle{ s_y=D(P,Q,f) }[/math]在f中是线性的，因此可以推出[math]\displaystyle{ \alpha s_x+\beta s_y+\gamma=D(P,Q,\alpha S_x+\beta S_y+\gamma U) }[/math](其中U={1,1,1,1})。任何策略的[math]\displaystyle{ D(P,Q,\alpha S_x+\beta S_y+\gamma U)=0 }[/math]被定义为零决定策略，长期收益服从关系式[math]\displaystyle{ \alpha s_x+\beta s_y+\gamma=0 }[/math]。


针锋相对是一种零决定策略，在不获得超越其他玩家优势的意义下是“公平”的。然而，零决定策略空间还包含这样的策略：在两个玩家的情况下，可以允许一个玩家单方面设置另一个玩家的分数，或者强迫进化的玩家获得比他自己的分数低一些的收益。被勒索的玩家可能会背叛，但会因此获得较低的回报并且受到伤害。因此，勒索的解决方案将重复囚徒困境转化为一种最后通牒博弈 ultimatum game。具体来说，X能够选择一种策略，对于这种策略，[math]\displaystyle{ D(P,Q,\beta S_y+\gamma U)=0 }[/math]单方面地将[math]\displaystyle{ s_y }[/math]设置为一个特定值范围内的特定值，与Y的策略无关，为X提供了“勒索”玩家Y的机会(反之亦然)。(事实证明，如果X试图将[math]\displaystyle{ s_x }[/math]设置为一个特定的值，那么可能的范围要小得多，只包括完全合作或完全叛变。[18])


重复囚徒困境的一个扩展是进化的随机重复囚徒困境，其中允许特定策略的相对丰度改变，更成功的策略相对增加。这个过程可以通过让不太成功的玩家模仿更成功的策略，或者通过从游戏中淘汰不太成功的玩家，同时让更成功的玩家成倍增加。研究表明，不公平的零决定策略不是进化稳定策略。关键的直觉告诉我们，进化稳定策略不仅要能够入侵另一个群体(这是勒索零决定策略可以做到的) ，而且还要在同类型的其他玩家面前表现良好(勒索零决定策略玩家表现不佳，因为他们减少了彼此的盈余)。[19]


理论和模拟证实，超过一个临界种群规模，零决定勒索在与更多合作策略的进化竞争中会失败，因此，种群越大，种群的平均收益就越大。此外，在某些情况下，勒索者甚至可能通过帮助打破统一的背叛者与使用“赢-保持-输”策略的转换玩家之间的对峙而促进合作。[11]


虽然勒索零决定策略在人口众多的情况下并不稳定，但另一种宽松的零决定策略既稳定又稳健。事实上，当人口不算太少的时候，这些策略可以取代任何其他零决定策略，甚至在一系列针对重复囚徒困境的广泛通用策略（包括“获胜-保持-输”的转换策略）中表现良好。亚历山大·斯图尔特 Alexander Stewart和约书亚·普洛特金 Joshua Plotkin在2013年的捐赠博弈中证明了这一点。[20]宽松的策略会与其他合作的玩家合作，面对背叛，慷慨的玩家比他的对手失去更多的效用。宽松策略是零决定策略和所谓的“好”策略的交集，阿金(2013) [21] 在良好的策略中，慷慨 (ZD) 子集在人口不是太小时时表现良好。 如果人口非常少，叛逃策略往往占主导地位。将这两种策略定义为玩家对过去的相互合作作出回应，并在至少获得合作预期收益的情况下平均分配预期收益的策略。在好的策略中，当总体不太小时，宽松(零决定)子集表现良好。如果总体很少，背叛策略往往占主导地位。[20]


连续重复囚徒困境

关于重复囚徒困境的研究大多集中在离散情况下，在这种情况下，参与者要么合作，要么背叛，因为这个模型分析起来比较简单。然而，一些研究人员已经研究了连续重复囚徒困境模型，在这个模型中，玩家能够对另一个玩家做出可变的贡献。乐 Le和博伊德 Boyd[22]发现，在这种情况下，合作比离散重复的囚徒困境更难发展。这个结果的基本直觉很简单: 在一个持续的囚徒困境中，如果一个人群开始处于非合作均衡状态，那么与非合作者相比，合作程度稍高的玩家不会从相互配合中获益。相比之下，在离散的囚徒困境中，相对于非合作者，针锋相对的合作者在非合作均衡中相互配合会获得巨大的回报。由于自然界可以提供更多的机会来进行各种各样的合作，而不是严格地将合作或背叛分为两类，因此连续的囚徒困境可以帮助解释为什么现实生活中针锋相对的合作的例子在自然界中极其罕见。（例如，哈默斯坦 Hammerstein [23]）。


尽管在理论模型中，针锋相对策略似乎是稳健的。


稳定策略的出现

玩家似乎不能协调相互合作，因此常常陷入劣等而稳定的背叛策略。这样，重复回合可以促进稳定策略的发展。[24]重复回合往往产生新颖的策略，这对复杂的社会互动有影响。其中一个策略就是“赢-保持-输”的转变。这个策略比一个简单的针锋相对策略要好 –也就是说，如果你能逃脱作弊的惩罚，就重复这个行为，如果你被抓住了，就改变策略。[25]


这种针锋相对策略的唯一问题是它们很容易出现信号错误。当一个人因报复而作弊，而另一个人将其单纯解释为欺骗时，就会出现问题。结果，第二个人现在作弊，然后在接下来的连锁反应中开始了反复交替的作弊模式。


现实生活的例子

囚犯的环境似乎是人为的，但实际上，在人类交往以及自然界的交互中有许多具有相同收益矩阵的例子。因此，囚徒困境是经济学、政治学、社会学等社会科学以及动物行为学、进化生物学等生物学研究的热点问题。许多自然过程都被抽象为生物进行无休止的囚徒困境博弈的模型。囚徒困境这种广泛的适用性让博弈变得非常重要。


环境研究

在环境研究中，囚徒困境在诸如全球气候变化等危机中显而易见。有人认为，所有国家都将从稳定的气候中受益，但是每一个国家通常都在限制二氧化碳排放方面犹豫不决。人们错误地认为，如果所有国家的行为都改变，任何一个国家保持目前的行为所带来的直接好处都会大于所谓的最终好处，这就解释了2007年气候变化方面的僵局。[26]


气候变化政治与囚徒困境之间的一个重要区别是不确定性; 污染对气候变化的影响程度和速度尚不清楚。因此，政府面临的困境不同于囚徒困境，因为合作的回报是未知的。这种差异表明，各国之间的合作远远少于真正的重复囚徒困境中的合作，因此避免可能发生的气候灾难的可能性远远小于使用真正的重复囚徒困境博弈论情景分析[27]


欧桑 Osang和南迪 Nandy (2003)提供了一个理论解释，并根据迈克尔·波特 Michael Porter的假设，即政府对竞争企业的监管是实质性的，证明了监管驱动的双赢局面。[28]


动物

许多动物的合作行为可以理解为囚徒困境的一个例子。通常动物会建立长期的伙伴关系，这种关系可以更具体地模拟为重复囚徒困境。例如，孔雀鱼成群结队地合作监察捕食者，它们被认为是在惩罚不合作的监察者。


吸血蝙蝠是从事相互的食物交换的群居动物。应用囚徒困境收益可以帮助解释这种行为: [29]


  • 合作/合作："回报：我在不幸运的晚上得到了能让我果腹的血，那在幸运的晚上我也应该分出点血，那不会花费多少。"
  • 背叛/合作："诱惑：你在我的不幸的夜里救了我，但在我的幸运夜我不会给你血，那样我会活的更好。"
  • 合作/叛变："可怜者的回报：在我的幸运夜我救了你的命，但在我的不幸夜里你没有救我，我有饿死的风险。"
  • 叛变/叛变："惩罚：我在我的幸运夜里不必付出代价来救你，但我在我的不幸夜里有挨饿的风险。"


心理学

在成瘾研究/行为经济学中，乔治·安斯利 George Ainslie指出[30]，可以将成瘾视为成瘾者现在和未来自我之间的跨期囚徒困境问题。在这种情况下，背叛意味着复发，很容易看出，目前和未来都没有背叛是迄今为止最好的结果。如果一个人今天戒了，但在将来又复吸，这是最糟糕的结果 –从某种意义上来说，今天戒瘾所包含的纪律和自我牺牲已经被“浪费”了，因为未来的复吸意味着瘾君子又回到了他开始的地方，他将被迫重新开始(这相当令人沮丧，也使得重新开始更加困难)。今天和明天复发是一个稍微“好一点”的结果，因为尽管瘾君子仍然上瘾，但他们没有努力去尝试停止。最后一种情况是，现在与成瘾斗争的任何人都会熟悉现在的成瘾行为，而在明天放弃。这里的问题是(和其他囚徒困境问题一样)，背叛“今天”有一个明显的好处，但明天这个人将面临同样的囚徒困境问题，同样明显的好处是背叛，最终导致一连串无休止的背叛。


约翰·高特曼 John Gottman在他的研究《信任的科学 the science of trust》中将良好的关系定义为伙伴知道不进入(背叛，背叛)牢房中或者至少不要陷入这样的动态循环关系中。


经济学

囚徒困境被称为社会心理学中的“大肠杆菌”，它被广泛用于研究寡头垄断竞争和集体行动来产生集体利益等问题。[31]


广告有时被认为是囚徒困境的一个真实例子。当香烟广告在美国是合法的时候，相互竞争的香烟制造商必须决定在广告上花多少钱。公司A的广告效果部分取决于公司B的广告效果。同样，公司B的广告带来的利润也受到公司A的广告影响。如果公司A和公司B都选择在给定的时间段内做广告，那么一家公司的广告就会抵消另一方的广告，倘若收入保持不变，费用就会因广告成本而增加。两家公司都将从广告减少中获益。然而，如果B公司选择不做广告，A公司就可以通过广告获得巨大的利益。尽管如此，一家公司的最佳广告数量仍取决于另一家公司的广告投放量。由于最佳策略取决于其他公司的选择，因此这里没有占主导地位的策略，这使得它与囚徒困境略有不同。但结果是相似的，如果两家公司的广告都少于均衡状态，他们的处境会更好。有时合作行为确实会在商业环境中出现。例如，香烟制造商支持立法禁止香烟广告，因为这将降低成本并增加整个行业的利润。这种分析可能适用于许多其他涉及广告的商业情况。


没有可强制执行的协议，卡特尔 cartel的成员国也会陷入(多玩家)囚徒困境。[32] “合作”通常意味着将价格保持在预先商定的最低水平。“背叛”意味着低于最低价格水平销售，并立即从其他卡特尔成员那里获得业务(和利润)。反垄断机构希望潜在的卡特尔成员相互背叛，确保消费者获得尽可能低的价格。


运动Sport

体育运动中的兴奋剂被认为是囚徒困境的一个例子。[33]


两名参赛运动员可以选择使用非法或危险药物来提高成绩。如果两个运动员都没有服用这种药物，那么他们都不会获得优势。如果只有一个人这样做，那么这个运动员就比他们的竞争对手获得了明显的优势，但由于法律或服用药物的医疗风险，这种优势会减少。然而，如果两名运动员都服用了这种药物，那么好处就被抵消了，只剩下风险，这使得他们的处境比没有服用兴奋剂的情况更加糟糕。[33]


国际政治

在国际政治理论中，囚徒困境经常被用来证明战略现实主义的一致性，这种战略现实主义认为，在国际关系中，由于国际无政府状态，所有国家(无论其国内政策或公开宣称的意识形态如何)都会为了自身的理性利益来行动。一个典型的例子是类似冷战和类似冲突的军备竞赛。[34]在冷战期间，北约和华约组织的对立联盟都可以选择武装或解除武装。从双方的观点来看，解除武装而对手继续武装可能会导致军事劣势和被歼灭。相反，如果选择武装而对手已经解除了武装，那么就会获得优势。如果双方都选择武装自己，那么任何一方都承担不起攻击对方的代价，但是双方都为发展和维持核武库付出了高昂的代价。如果双方都选择裁军，战争就可以避免，也不会有任何代价。


虽然最好的结果是双方解除武装，但是双方的理性选择是武装起来，事实也的确如此。在接下来的三十年里，双方都在军事研究和武器装备的消耗战上投入了大量的资源，直到苏联无法承受经济损失。[35]同样的逻辑也适用于任何类似的情况，无论是主权国家之间的经济竞争还是技术竞争。


多玩家困境

许多现实生活中的困境牵涉到多个参与者。[36]尽管具有隐喻性，但哈丁的公地悲剧 tragedy of the commons可以看作是囚徒困境多个参与者的一个例子: 每个村民做出选择是为了个人利益还是克制。对于一致(甚至频繁)叛变的集体回报是非常低的(代表了对“公共资源”的破坏)。大多数人可能会遇到的公地困境是在一个共用的房子里洗碗。通过不洗碗，个人可以节省时间，但如果每个居民都选择这种行为，那么集体的代价是任何人都没有干净的盘子。


公共资源并不总是被利用: 威廉·庞德斯通 William Poundstone在一本关于囚徒困境的书(见下文参考文献)中描述了新西兰的一种情况，信箱没有上锁。人们可以不付钱就拿报纸(背叛) ，但很少有人这样做，他们觉得如果他们不付钱，那么其他人也不会付钱，这会摧毁整个系统。2009年诺贝尔经济学奖获得者埃莉诺·奥斯特罗姆 Elinor Ostrom随后的研究认为公地悲剧过于简单化，其负面结果会受到外部影响。在没有复杂压力的情况下，团体之间为了共同利益进行沟通和管理，执行社会规范以保护资源并为团体实现最大利益，这是实现囚徒困境最佳结果的一个例子。[37]


相关博弈

封闭袋子交换

囚徒困境是一个公文包式的交换


侯世达 Douglas Hofstadter [38]曾经指出，人们通常会发现诸如囚徒困境的问题，比如，当它以一个简单囚徒困境博弈的形式，或者以权衡的方式表现出来时，会更容易理解。他使用的几个例子之一是“封闭袋子交换” :

两人相遇并交换包裹，事先知道一个包里装着钱，一个装着订单。任一玩家都可选择尊重交易，放入事先约定的东西；也可以选择背叛，交换空的公文包。


背叛总是会带来一个理论上更可取的结果。[39]


朋友还是敌人？

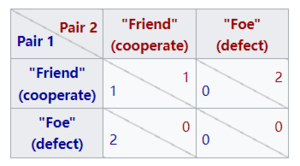
朋友还是敌人？是一个竞赛节目，从2002年至2005年在美国的Game show Network播出。这是囚徒困境博弈在真人身上测试的一个例子，只是在人为的环境中。在游戏节目中，有三对选手参加比赛。当一对被淘汰时，他们会玩一个类似囚徒困境的游戏来决定奖金如何分配。如果他们都合作(朋友) ，他们分享奖金50-50。如果一方合作而另一方背叛(敌人) ，那么叛变者将得到所有的奖金，而合作者将一无所获。如果双方都背叛，那么双方都将一无所有。请注意，奖励矩阵与上面给出的标准矩阵略有不同，因为“双方都背叛”和“合作而对方背叛”情况下的奖励是相同的。与标准囚徒困境中的严格均衡相比，这使得“两个都背叛”情况成为一个弱均衡。如果一个参赛者知道他们的对手将投票给“敌人” ，那么他们自己的选择不会影响他们自己的奖金。从特定意义上讲，“朋友还是敌人”节目在囚徒困境和“胆小鬼”博弈之间有一个奖励模型。


奖励矩阵是

奖励矩阵.png


英国电视节目《相信我 Trust Me》、《阴影 Shafted》、《银行工作 The Bank Job》和《黄金球 Golden Balls》以及美国电视节目《单身公寓 Bachelor Pad》和《全部拿走 Take It All》也采用了这种奖励矩阵。一个经济学家团队分析了“黄金球”系列的游戏数据，他们发现，现实生活中，合作对于金额而言“惊人地高” ，但在游戏的背景下，相对较低。[40]


重复雪堆

来自洛桑大学和爱丁堡大学的研究人员认为，“重复雪堆游戏”可能更能反映现实世界的社会状况。虽然这个模型实际上是一个胆小鬼博弈。在这个模型中，由于背叛可以降低被剥削的风险，个体总是从合作选择中获益。这个雪堆游戏可以设想两个司机被困在雪堆的两侧，每个司机都可以选择铲雪清理道路，或者留在自己的车里。一个玩家的最高回报来自于让对手清除所有的积雪，但是仍然可以从对手的工作中得到回报。


这可能更好地反映了现实世界的情景，研究人员举了两位科学家合作完成一份报告的例子，如果另一位科学家更加努力地工作，这两位科学家都会受益。“但当你的合作者不做任何工作时，你自己完成所有的工作可能会更好。你最终还是会完成一个项目。” [41]

重复雪堆.png

协调博弈

在协调博弈中，参与者必须协调自己的策略以获得一个好的结果。一个例子是两辆车在暴风雪中突然相遇，每辆车必须选择是左转还是右转。如果两辆车都向左转弯，或者都向右转弯，那么两辆车就不会相撞。当地的左右向交通惯例有助于协调他们的行动。


对称的协调游戏包括猎鹿 Stag hunt和巴赫 Bach或斯特拉文斯基 Stravinsky。


不对称的囚徒困境

一个更一般的博弈集是不对称的。就像在囚徒困境中一样，最好的结果是合作，而背叛是有动机的。与对称的囚徒困境不同的是一个玩家比另一个玩家有更多的损失或收获。这样的博弈被描述为囚徒困境，其中一个囚徒有不在场证明，这就是术语“不在场证明游戏”的由来。[42]


在实验中，在重复博弈中获得不均等收益的参与者可能会寻求利润最大化，但是前提是两个玩家都必须获得均等的收益。这可能会导致一个稳定的均衡策略，即弱势参与者在每隔X场博弈中都会背叛，而另一个参与者总是保持合作。这种行为可能取决于实验围绕公平的社会规范。[43]


软件

已经有一些可以用来运行囚徒困境模拟和比赛的软件包，其中一些有可用的源代码。


在小说中

汉努·拉贾尼埃米 Hannu Rajaniemi将他的《量子窃贼》三部曲的开场场景设置在一个“囚徒困境”中。该系列的主题被描述为“双重宇宙的不足” ，最终的对手是一个叫做全面背叛者的角色。作为一个处理这个问题的艺术家，拉贾尼埃米尤其有趣，因为他是剑桥大学培养的数学家，拥有数学物理学博士学位——物质和信息的可互换性是这本书的一个主要特征，它发生在后奇点 post-singularity的未来。该系列的第一本书于2010年出版，其续集《分形王子》和《因果天使》分别于2012年和2014年出版。


一个（重复）囚徒困境博弈的模型是2012年电子游戏《零度逃脱: 美德的最后奖励》的重点，也是2016年续集《零度逃脱: 极限脱出刻之困境》的一个次要部分。


在特伦顿·李·斯图尔特 Trenton Lee Stewart的《神秘的本尼迪克特社会和囚徒困境 The Mysterious Benedict Society and the Prisoner's Dilemma》中，主要角色从玩一个版本的游戏开始，然后一起逃离“监狱”。后来他们变成了真正的囚犯，再次越狱。


在冒险区: 苦难游戏的平衡中，玩家角色在他们在两个领域的时间内两次呈现出囚徒困境，一次是合作，一次是背叛。


在作者詹姆斯·S·A·科里·提亚玛特 James S. A. Corey Tiamat的《愤怒 Wrath》中的第八部小说中，温斯顿•杜阿尔特 Winston Duarte向他14岁的女儿特蕾莎 Teresa解释了她面临的囚徒困境，来训练她的战略思维能力。


请参阅

参考文献

  1. ↑ Poundstone, 1992
  2. ↑ Milovsky, Nicholas. "The Basics of Game Theory and Associated Games". Retrieved 11 February 2014.
  3. ↑ Fehr, Ernst; Fischbacher, Urs (Oct 23, 2003). "The Nature of human altruism" (PDF). Nature. 425 (6960): 785–91. Bibcode:2003Natur.425..785F. doi:10.1038/nature02043. PMID 14574401. Retrieved February 27, 2013.
  4. ↑ Tversky, Amos; Shafir, Eldar (2004). Preference, belief, and similarity: selected writings.. Massachusetts Institute of Technology Press. ISBN 9780262700931. http://cseweb.ucsd.edu/~gary/PAPER-SUGGESTIONS/Preference,%20Belief,%20and%20Similarity%20Selected%20Writings%20(Bradford%20Books).pdf. Retrieved February 27, 2013. 
  5. ↑ Toh-Kyeong, Ahn; Ostrom, Elinor; Walker, James (Sep 5, 2002). "Incorporating Motivational Heterogeneity into Game-Theoretic Models of Collective Action" (PDF). Public Choice. 117 (3–4): 295–314. doi:10.1023/b:puch.0000003739.54365.fd. hdl:10535/4697. Retrieved June 27, 2015.
  6. ↑ Oosterbeek, Hessel; Sloof, Randolph; Van de Kuilen, Gus (Dec 3, 2003). "Cultural Differences in Ultimatum Game Experiments: Evidence from a Meta-Analysis" (PDF). Experimental Economics. 7 (2): 171–88. doi:10.1023/B:EXEC.0000026978.14316.74. Archived from the original (PDF) on May 12, 2013. Retrieved February 27, 2013.
  7. ↑ Ormerod, Paul (2010-12-22). Why Most Things Fail. ISBN 9780571266142. https://books.google.com/?id=WIhZlB86nJwC&pg=PT96&lpg=PT96&dq=rand+secretaries+prisoner%27s+dilemma#v=onepage. 
  8. ↑ Deutsch, M. (1958). Trust and suspicion. Journal of Conflict Resolution, 2(4), 265–279. https://doi.org/10.1177/002200275800200401
  9. ↑ Rapoport, A., & Chammah, A. M. (1965). Prisoner’s Dilemma: A study of conflict and cooperation. Ann Arbor, MI: University of Michigan Press.
  10. ↑ Kaznatcheev, Artem (March 2, 2015). "Short history of iterated prisoner's dilemma tournaments". Journal of Conflict Resolution. 24 (3): 379–403. doi:10.1177/002200278002400301. Retrieved February 8, 2016.
  11. ↑ 11.0 11.1 Hilbe, Christian; Martin A. Nowak; Karl Sigmund (April 2013). "Evolution of extortion in Iterated Prisoner's Dilemma games". PNAS. 110 (17): 6913–18. arXiv:1212.1067. Bibcode:2013PNAS..110.6913H. doi:10.1073/pnas.1214834110. PMC 3637695. PMID 23572576.
  12. ↑ Shy, Oz (1995). Industrial Organization: Theory and Applications. Massachusetts Institute of Technology Press. ISBN 978-0262193665. https://books.google.com/?id=tr4CjJ5LlRcC&pg=PR13&dq=industrial+organization+theory+and+applications. Retrieved February 27, 2013. 
  13. ↑ Dal Bó, Pedro; Fréchette, Guillaume R. (2019). "Strategy Choice in the Infinitely Repeated Prisoner's Dilemma". American Economic Review (in English). 109 (11): 3929–3952. doi:10.1257/aer.20181480. ISSN 0002-8282.
  14. ↑ http://www.pnas.org/content/pnas/93/7/2686.full.pdf
  15. ↑ "Bayesian Nash equilibrium; a statistical test of the hypothesis" (PDF). Tel Aviv University. Archived from the original (PDF) on 2005-10-02.
  16. ↑ Wu, Jiadong; Zhao, Chengye (2019), Sun, Xiaoming; He, Kun; Chen, Xiaoyun (eds.), "Cooperation on the Monte Carlo Rule: Prisoner's Dilemma Game on the Grid", Theoretical Computer Science (in English), Springer Singapore, vol. 1069, pp. 3–15, doi:10.1007/978-981-15-0105-0_1, ISBN 978-981-15-0104-3
  17. ↑ University of Southampton team wins Prisoner's Dilemma competition, University of Southampton, 7 October 2004{{citation}}: CS1 maint: url-status (link)
  18. ↑ 18.0 18.1 18.2 18.3 18.4 Press, WH; Dyson, FJ (26 June 2012). "Iterated Prisoner's Dilemma contains strategies that dominate any evolutionary opponent". Proceedings of the National Academy of Sciences of the United States of America. 109 (26): 10409–13. Bibcode:2012PNAS..10910409P. doi:10.1073/pnas.1206569109. PMC 3387070. PMID 22615375.
  19. ↑ Adami, Christoph; Arend Hintze (2013). "Evolutionary instability of Zero Determinant strategies demonstrates that winning isn't everything". Nature Communications. 4: 3. arXiv:1208.2666. Bibcode:2013NatCo...4.2193A. doi:10.1038/ncomms3193. PMC 3741637. PMID 23903782.
  20. ↑ 20.0 20.1 Stewart, Alexander J.; Joshua B. Plotkin (2013). "From extortion to generosity, evolution in the Iterated Prisoner's Dilemma". Proceedings of the National Academy of Sciences of the United States of America. 110 (38): 15348–53. Bibcode:2013PNAS..11015348S. doi:10.1073/pnas.1306246110. PMC 3780848. PMID 24003115.
  21. ↑ Akin, Ethan (2013). "Stable Cooperative Solutions for the Iterated Prisoner's Dilemma". p. 9. arXiv:1211.0969 [math.DS].
  22. ↑ Le, S.; Boyd, R. (2007). "Evolutionary Dynamics of the Continuous Iterated Prisoner's Dilemma". Journal of Theoretical Biology. 245 (2): 258–67. doi:10.1016/j.jtbi.2006.09.016. PMID 17125798. {{cite journal}}: Unknown parameter |name-list-format= ignored (help)
  23. ↑ Hammerstein, P. (2003). Why is reciprocity so rare in social animals? A protestant appeal. In: P. Hammerstein, Editor, Genetic and Cultural Evolution of Cooperation, MIT Press. pp. 83–94.
  24. ↑ Spaniel, William (2011). Game Theory 101: The Complete Textbook. 
  25. ↑ Nowak, Martin; Karl Sigmund (1993). "A strategy of win-stay, lose-shift that outperforms tit-for-tat in the Prisoner's Dilemma game". Nature. 364 (6432): 56–58. Bibcode:1993Natur.364...56N. doi:10.1038/364056a0. PMID 8316296.
  26. ↑ "Markets & Data". The Economist. 2007-09-27.
  27. ↑ Rehmeyer, Julie (2012-10-29). "Game theory suggests current climate negotiations won't avert catastrophe". Science News. Society for Science & the Public.
  28. ↑ Osang, Thomas; Nandyyz, Arundhati (August 2003). Environmental Regulation of Polluting Firms: Porter's Hypothesis Revisited (PDF) (paper).
  29. ↑ Dawkins, Richard (1976). The Selfish Gene. Oxford University Press. 
  30. ↑ Ainslie, George (2001). Breakdown of Will. ISBN 978-0-521-59694-7. 
  31. ↑ Axelrod, Robert (1980). "Effective Choice in the Prisoner's Dilemma". The Journal of Conflict Resolution. 24 (1): 3–25. doi:10.1177/002200278002400101. ISSN 0022-0027. JSTOR 173932.
  32. ↑ Nicholson, Walter (2000). Intermediate microeconomics and its application (8th ed.). Fort Worth, TX: Dryden Press : Harcourt College Publishers. ISBN 978-0-030-25916-6. 
  33. ↑ 33.0 33.1 Schneier, Bruce (2012-10-26). "Lance Armstrong and the Prisoners' Dilemma of Doping in Professional Sports | Wired Opinion". Wired. Wired.com. Retrieved 2012-10-29.
  34. ↑ Stephen J. Majeski (1984). "Arms races as iterated prisoner's dilemma games". Mathematical and Social Sciences. 7 (3): 253–66. doi:10.1016/0165-4896(84)90022-2.
  35. ↑ Kuhn, Steven (2019), "Prisoner's Dilemma", in Zalta, Edward N. (ed.), The Stanford Encyclopedia of Philosophy (Winter 2019 ed.), Metaphysics Research Lab, Stanford University, retrieved 2020-04-12
  36. ↑ Gokhale CS, Traulsen A. Evolutionary games in the multiverse. Proceedings of the National Academy of Sciences. 2010 Mar 23. 107(12):5500–04.
  37. ↑ "The Volokh Conspiracy " Elinor Ostrom and the Tragedy of the Commons". Volokh.com. 2009-10-12. Retrieved 2011-12-17.
  38. ↑ Hofstadter, Douglas R. (1985). "Ch.29 The Prisoner's Dilemma Computer Tournaments and the Evolution of Cooperation.". Metamagical Themas: questing for the essence of mind and pattern. Bantam Dell Pub Group. ISBN 978-0-465-04566-2. 
  39. ↑ "Prisoner's dilemma - Wikipedia, the free encyclopedia". users.auth.gr. Retrieved 2020-04-12.
  40. ↑ Van den Assem, Martijn J. (January 2012). "Split or Steal? Cooperative Behavior When the Stakes Are Large" (PDF). Management Science. 58 (1): 2–20. doi:10.1287/mnsc.1110.1413. SSRN 1592456.
  41. ↑ Kümmerli, Rolf. "'Snowdrift' game tops 'Prisoner's Dilemma' in explaining cooperation". Retrieved 11 April 2012.
  42. ↑ Robinson, D.R.; Goforth, D.J. (May 5, 2004). Alibi games: the Asymmetric Prisoner' s Dilemmas (PDF). Meetings of the Canadian Economics Association, Toronto, June 4-6, 2004.
  43. ↑ Beckenkamp, Martin; Hennig-Schmidt, Heike; Maier-Rigaud, Frank P. (March 4, 2007), "Cooperation in Symmetric and Asymmetric Prisoner's Dilemma Games" (PDF), Max Planck Institute for Research on Collective Goods


拓展阅读

  • S.M. Amadae (2016). 'Prisoner's Dilemma,' Prisoners of Reason. Cambridge University Press, NY, pp. 24–61.
  • Aumann, Robert (1959). "Acceptable points in general cooperative n-person games". In Luce, R. D.; Tucker, A. W.. Contributions to the Theory 23 of Games IV. Annals of Mathematics Study. 40. Princeton NJ: Princeton University Press. pp. 287–324. MR 0104521. 
  • Cristina Bicchieri (1993). Rationality and Coordination. Cambridge University Press.
  • Melvin Dresher (1961). The Mathematics of Games of Strategy: Theory and Applications Prentice-Hall, Englewood Cliffs, NJ.
  • Greif, A. (2006). Institutions and the Path to the Modern Economy: Lessons from Medieval Trade. Cambridge University Press, Cambridge, UK.
  • Anatol Rapoport and Albert M. Chammah (1965). Prisoner's Dilemma. University of Michigan Press.


外部链接


编者推荐

行为博弈视角中的群体协调课程 本课程重点关注了不同信息反馈方式下的群体协调行为，并对结果从心理学角度进行解读，以期为社会预期管理问题的解决提供一定的参考

下为一些链接(源于集智俱乐部公众号)能够更好的了解博弈论的相关信息： 来自YouTube上面的Complexity Labs（Complexity Labs是一个专门介绍复杂系统领域知识的在线学习网站）

来自集智学园关于博弈论的相关课程

此外，还有根据纳什的传记改编的电源

本书在对风险领域研究的开创性意义方面值得关注。丹·加德纳作为一位资深的媒体记者，能够静下心来系统探讨关乎人们身心健康的风险与恐惧问题，着实不易，而丹·加德纳却令人信服地做到了。


本中文词条由Henry翻译，Smile审校，薄荷编辑，如有问题，欢迎在讨论页面留言。

本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

取自“https://wiki.swarma.org/index.php?title=囚徒困境&oldid=26894”