对称性破缺
在物理学中,一个作用于系统的(无限)小扰动使系统跨过临界点,通过决定去向分叉的哪个分支来决定系统的命运,这种现象叫做对称性破缺。对于一个观测不到扰动(或“噪声”)的外部观察者来说,这个选择看起来是任意的。这个过程被称为对称性破缺,因为这种转变通常使系统从一个对称但无序的状态进入一个或多个确定的状态。在斑图生成中对称性破缺起着重要作用。
1972年,诺贝尔奖得主P·W·安德森 P.W.Anderson在《科学(Science)》杂志上发表了一篇名为《多则异也("More is different")》的论文[1],文中使用对称性破缺的思想表明,即使还原论是正确的,但它的逆命题建构主义是错误的。建构主义认为,在给出描述各组成部分的理论的情况下科学家可以轻易地预测复杂现象。
对称性破缺可以分为显性对称性破缺和自发对称性破缺两种类型,二者的区别是,在破缺对称性下系统的运动方程是否不变或者基态是否保持不变。
显性对称性破缺
在显性对称性破缺中,描述系统的运动方程在破缺对称下是不同的。在哈密顿力学或拉格朗日力学中,假若系统的哈密顿量(或拉格朗日量)中至少一项显性地打破了给定的对称性,就发生了显性对称性破缺。
自发对称性破缺
在自发对称性破缺中,系统的运动方程是不变的,但系统发生了变化。这是因为系统的背景(时空)——真空态——是非恒定的。这种对称性破缺可以用一个序参量进行参数化。这类对称破缺的一个特殊情况是动力学对称性破缺。
自发对称破缺是一个自发的对称破缺过程,它使处于对称状态的物理系统最终处于非对称状态。特别地,它可以描述运动方程或拉格朗日方程服从某种对称性,但最低能量真空解不具有该对称性的系统。当系统进入其中一个真空解时,真空解周围的扰动会破坏系统对称性,尽管整个拉格朗日方程仍然保持了对称性。
例子
势
考虑一个对称向上的圆顶,底部环绕着一个槽。如果把一个球放在圆顶的最顶端,这个系统是围绕中心轴旋转对称的。但球体可能会沿着穹顶滚动到能量最低的槽中,从而自发地打破这种对称性。然后,球在圆周上某个固定的点上停下来。圆顶和球保持了各自的对称,但系统却没有保持对称性。[2]
在最简单的理想相对论模型中,可以用一个解释性的标量场理论总结自发对称性破缺。一个标量场[math]\displaystyle{ \phi }[/math]的拉格朗日量从本质上决定了系统的行为,它可以分解成动能项和势能项:
-
[math]\displaystyle{ \mathcal{L} = \partial^\mu \phi \partial_\mu \phi - V(\phi). }[/math]
(1)
-
正是在势能项 [math]\displaystyle{ V(\phi) }[/math] 中触发了对称性破缺。例如左图所示的Jeffrey Goldstone [3]给出的势能函数:
-
[math]\displaystyle{ V(\phi) = -5|\phi|^2 + |\phi|^4 \, }[/math].
(2)
-
该势函数具有无穷数量的最小值点(真空态)当
-
[math]\displaystyle{ \phi = \sqrt{5} e^{i\theta} }[/math].
(3)
-
其中θ可以取0到2π之间的任何实数。系统也有一个不稳定的真空状态,对应于Φ = 0。这个状态具有U(1)对称。然而,一旦系统落入某个稳定真空状态(相当于选择θ),这种对称性就会消失,或者说“自发破缺”。
事实上,任何其他θ的选择都将具有完全相同的能量,这意味着无质量的Nambu–Goldstone玻色子的存在,这种模式在势能的最小值绕圆周运动,这也表明存在拉格朗日方程中原始对称性的一些记忆。
其他例子
- 对于铁磁性材料,其基本物理定律在空间旋转下是不变的。在这里,序参量是衡量磁偶极子密度的磁化强度。在居里温度以上,序参量为零,具有空间不变性,不存在对称性破缺。然而,在居里温度以下,磁化强度变成一个恒定的非零值,指向一个特定的方向(在有充分平衡的理想情况下;否则,平移对称性也会破缺)。使该向量方向不变的旋转对称性仍然保留,而其他旋转对称性自发破缺。
- 描述固体的物理定律在完整的欧几里得群下是不变的,但固体本身会自发地将这个群分解为一个空间群。其中位移和方向是序参量。
- 广义相对论具有洛伦兹对称性,但在FRW宇宙模型中,定义为星系速度平均值(星系在宇宙尺度上的行为就像气体粒子)的平均4-速度场,作为序参量会打破这种对称性。对于宇宙微波背景辐射也有类似的评论。
- 对于电弱模型,如前面所解释的,希格斯场的一个分量提供了将电弱规范对称性破缺到电磁规范对称性的序参量。和铁磁的例子一样,在电弱温度下也有相变。同样地由于我们不倾向于注意对称性破缺,导致我们花了这么长时间才发现电弱统一。
- 在超导体中有一个凝聚态集体场ψ,它是打破电磁规范对称性的序参量。
- 拿一个细长的圆柱形塑料杆,把两端推到一起。在屈曲之前,系统在旋转下是对称的,因此具有圆柱对称性。但在弯曲之后,它看起来就不同了,而且是不对称的。然而,圆柱对称性的特征仍然存在:忽略摩擦,杆可以不受外力自由地自旋,在时间上取代基态,相当于一个频率趋于零的振荡,而不是沿屈曲方向的径向振荡。这种自旋模式实际上是必需的Nambu–Goldstone玻色子。
- 考虑无限水平面上的一层均匀的流体,这个系统具有欧几里得平面的所有对称性。但是现在均匀地加热底部表面,使它变得比上表面热得多。当温度梯度足够大时,就会形成对流单元,打破了欧几里得对称。
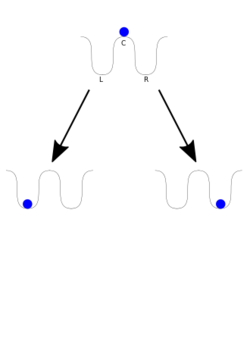
- 考虑一个围绕某个竖直的直径旋转的圆形箍上的珠子。当旋转速度从静止逐渐增加时,珠子最初会停留在环底部的初始平衡点(直观上稳定,重力势最低)。在一定的临界旋转速度下,这一点将变得不稳定,珠子将跳到另外两个新创建的离中心等距离的平衡点中的一个。起初,系统相对直径是对称的,但在通过临界速度后,珠子最终停留在两个新的平衡点中的一个,从而打破了对称性。
物理学中的自发对称性破缺
粒子物理
在粒子物理学中,载力子通常由规范对称的场方程表示;这些方程预测到某些测量值在场的任何点上都是相同的。例如,场方程可以预测两个夸克的质量和是常数。通过求解方程来求单个夸克的质量可能会得到两个解。在一个解中,夸克A比夸克B重;在第二个解中,夸克B比夸克A重,并且两个解中质量差相同。方程的对称性不是由单个解来反映的,而是由解的范围来反映的。
一个实际的测量只反映了一个解,这代表了其潜在理论的对称性的破缺。在这里“隐藏”是比“破缺”更好的术语,因为对称性总是存在于这些方程中。这种现象被称为自发对称破缺(SSB),因为(我们所知道的)没有任何东西会打破方程中的对称性。[4]
手性对称性
手性对称破缺是粒子物理中影响强相互作用手性对称的自发对称破缺的一个例子。手性对称性破缺是量子色动力学(描述这些相互作用的量子场理论)的一种特性,它是核子的大部分质量(超过99%)的成因,因此也是所有普通物质的主要成因,它将非常轻的束缚夸克转化为100倍重量的重子的成分。在这个自发对称破缺过程中,近似的Nambu–Goldstone玻色子是介子,其质量比核子的质量轻一个数量级。它是电弱对称破缺的希格斯机制的原型和重要组成部分。
希格斯机制
强、弱和电磁力都可以理解为来自规范对称。希格斯机制,即规范对称的自发对称破缺机制,是理解金属超导性和粒子物理标准模型中粒子质量起源的重要组成部分。区分真正的对称性和规范对称性的一个重要的结果,是规范对称性的自发破缺不产生典型的无质量Nambu-Goldstone物理模式,而只产生有质量的模式,像超导体中的等离子体模式,或者粒子物理学中观察到的希格斯模式。
在粒子物理的标准模型中,与电弱力相关的SU(2) × U(1)规范对称性自发破缺产生多种粒子的质量,并将电磁力和弱相互作用分离。W玻色子和Z玻色子是介导弱相互作用的基本粒子,而光子介导电磁相互作用。当能量远远大于100 GeV时,所有这些粒子的行为都相似。Weinberg-Salam理论预测,在较低的能量下,这种对称性被打破,光子和大质量的W和Z玻色子就会出现。[5]此外,费米子不断地产生质量。
在没有自发对称性破缺的情况下,基本粒子相互作用的标准模型要求大量粒子的存在。而一些粒子(W玻色子和Z玻色子)会被预测为无质量的,但实际上它们被观察到有质量。为了克服这个问题,希格斯机制增强了自发对称破缺,从而赋予这些粒子质量。它还表明一种新粒子——希格斯玻色子——的存在,它在2012年被实验探测到。
金属的超导性是一种类似于希格斯现象的凝聚态物质,其中库珀电子对的凝聚会自发地打破与光和电磁相关的U(1)规范对称性。
凝聚态物理
物质的大多数相态都可以通过自发对称性破缺的透镜来理解。例如,晶体是原子的周期性排列,它并非在所有平移下(仅在晶格向量平移的一个小子集下)都是不变的。磁体有朝向特定方向的南极和北极,打破了旋转对称。除了这些例子,还有一大堆其他的物质对称性破缺相——包括液晶的向列相、电荷和自旋密度波、超流体等等。
目前已知的不能用自发对称破缺来描述的几个例子包括:物质的拓扑有序相,如分数量子霍尔液体和自旋液体。这些状态并不破坏任何对称性,然而它们是物质的不同相。与自发对称破缺的情况不同,目前还没有一个描述这种状态的一般框架。[6]
连续对称性
铁磁体是正则系统,它在居里温度以下和h = 0(其中h为外部磁场)的情况下自发打破自旋的连续对称性。在居里温度以下,系统的能量在磁化强度m(x)的反转下(使m(x) =−m(−x))不变。当哈密顿量在反转变换下不变,而期望值不是恒定时,对称性在h→0时自发破坏。
物质的自发对称性破缺相由一个序参量表征,它描述了打破所考虑的对称性的量。例如,在磁铁中,序参量是局部磁化强度。
连续对称的自发破缺不可避免地伴随着无间隙(意味着这些模式不需要花费任何能量来激发)Nambu–Goldstone模式,它与序参量的缓慢、长波长波动有关。例如,晶体中的振动模式声子,与晶体原子的缓慢密度涨落有关。磁铁相关的Goldstone模式是自旋振荡波,称为自旋波。对于序参量不是守恒量的对称性破缺态,Nambu-Goldstone模通常是无质量的,并以恒定速度传播。
由Mermin和Wagner提出的一个重要定理指出,在有限温度下,Nambu–Goldstone模式热激活的扰动破坏了长程有序,并阻止了一维和二维系统中对称性的自发破缺。类似地,即使是在零温度下,序参量的量子涨落阻止了一维系统中大多数类型的连续对称破缺。(一个重要的例外是铁磁体,其序参量磁化强度是一个精确的守恒量,不存在任何量子涨落。)
其他长程相互作用系统,如圆柱曲面通过库仑势或汤川势相互作用,已被证明打破平移和旋转对称。[7]结果表明,在对称哈密顿量存在的情况下,在无限体积的极限下,系统自发地采用手性构型,即打破镜面对称。
动力学对称性破缺
动力学对称性破缺(DSB)是自发对称性破缺的一种特殊形式,在这种情况下,系统的基态相对理论描述(例如拉格朗日量)的对称性降低。
全局对称性的动力学破缺是自发对称性破缺,它不是发生在(经典)树的水平(例如在bare作用的水平),而是由于量子修正(例如在有效作用的水平)。
规范对称性动力学破缺更加微妙。在常规规范对称自发破缺理论中,存在一个不稳定的希格斯粒子,希格斯粒子驱动真空态进入对称破缺相。(例如,参见弱电相互作用。)然而,在规范对称性动力学破缺中,不存在不稳定的希格斯粒子,但系统本身的束缚态提供了导致相变的不稳定场。例如,巴丁、希尔和林德纳发表了一篇论文,试图用一个由顶-反顶夸克束缚状态驱动的DSB来取代标准模型中的传统希格斯机制。(在这种模型中,复合粒子扮演希格斯玻色子的角色,通常被称为“复合希格斯模型”。[8])规范对称性动力学破缺通常是由于费米凝聚的产生,例如夸克凝聚,它与量子色动力学中手性对称的动力学破缺有关。传统的超导性是凝聚态物质方面的典型例子,声子的吸引导致电子成对结合然后凝聚,从而打破电磁规范对称性。
广义描述和技术运用
要发生自发对称性破缺,系统中必须有几个等可能的结果,整个系统相对于这些结果是对称的。然而,如果对系统进行采样(即如果系统被实际使用或以任何方式与之交互),就必须产生特定的结果。虽然系统作为一个整体是对称的,但它从来没有表现出这种对称性,而只是处于一个特定的不对称状态。于是,在该理论中对称性被自发地打破了。然而,每个结果的可能性都相等这一点,反映了潜在的对称性。因此通常被称为“隐藏对称性”,并具有重要的形式结果。(参见有关Goldstone玻色子的文章。)
当一个理论相对于一个对称群是对称的,但要求群中的一个元素是不同的,那么就会发生自发对称性破缺。该理论不能规定哪个成员是不同的,而只能规定那个成员是不同的。从这一点开始,这个理论就可以被视为这个元素实际上是不同的,附带的条件是,任何以这种方式发现的结果必须是重新对称的,通过取组中每个元素的平均值作为不同的元素。
在物理理论中,最重要的概念是序参量。如果有一个场(通常是背景场)得到一个期望值(不一定是真空期望值),这个期望值在理论具有的对称性下不是不变的,我们就说系统处于有序相,对称性自发破缺。这是因为序参量指定了测量其他子系统与之相互作用的“参考框架”。在这种情况下,真空状态不服从初始对称性(这将保持它不变,在线性实现的Wigner模式中,它将是一个单线),而是在(隐藏的)对称下变化,现在在(非线性)Nambu–Goldstone模式中实现。通常,在没有希格斯机制的情况下,就会出现无质量的戈德斯通玻色子。
对称群可以是离散的,如晶体的空间群,也可以是连续的(如李群),如空间的旋转对称。然而,如果系统只包含一个空间维度,尽管经典解可能打破连续对称性,那么在全量子理论的真空状态下,只有离散的对称性可能被打破。
诺贝尔奖
2008年10月7日,瑞典皇家科学院(Royal Swedish Academy of Sciences)将2008年诺贝尔物理学奖授予三位科学家,以表彰他们在亚原子物理对称性破缺方面的工作。芝加哥大学的Yoichiro Nambu获得了一半的奖金,表彰他发现了在强相互作用下对称性自发破缺的机制,特别是手性对称性破缺。京都大学(Kyoto University)物理学家小林诚(Makoto Kobayashi)和正川俊英(Toshihide Maskawa)因发现了弱相互作用中CP对称性显性破缺的起源而分享了另一半奖金[9]。这一起源最终依赖于希格斯机制,但迄今为止被理解为希格斯耦合的“恰好如此”特征,而不是一种自发的对称破缺现象。
参见
- 自催化反应和秩序产生
- 灾难理论
- 手性对称性破缺
- CP破坏
- 费米球
- 引力规范理论
- Goldstone 玻色子
- 大统一理论
- 希格斯机制
- 希格斯玻色子
- 希格斯场(经典)
- 不可逆性
- 手性对称破缺的磁性催化
- Mermin–Wagner 理论
- 诺顿的圆顶
- 二阶相变
- 化学中自发绝对非对称合成
- 对称性破缺
- 快子凝聚
- 1964年PRL对称性破缺文章
注解
- Note that (as in fundamental Higgs driven spontaneous gauge symmetry breaking) the term "symmetry breaking" is a misnomer when applied to gauge symmetries.
参考文献
- ↑ Anderson, P.W. (1972). "More is Different" (PDF). Science. 177 (4047): 393–396. Bibcode:1972Sci...177..393A. doi:10.1126/science.177.4047.393. PMID 17796623.
- ↑ Edelman, Gerald M. (1992). Bright Air, Brilliant Fire: On the Matter of the Mind. New York: BasicBooks. p. 203. https://archive.org/details/brightairbrillia00gera.
- ↑ Goldstone, J. (1961). "Field theories with " Superconductor " solutions". Il Nuovo Cimento. 19 (1): 154–164. Bibcode:1961NCim...19..154G. doi:10.1007/BF02812722.
- ↑ Steven Weinberg (20 April 2011). Dreams of a Final Theory: The Scientist's Search for the Ultimate Laws of Nature. Knopf Doubleday Publishing Group. ISBN 978-0-307-78786-6. https://books.google.com/books?id=Rsg3PE_9_ccC.
- ↑ A Brief History of Time, Stephen Hawking, Bantam; 10th anniversary edition (1998). pp. 73–74.
- ↑ Chen, Xie; Gu, Zheng-Cheng; Wen, Xiao-Gang (2010). "Local unitary transformation, long-range quantum entanglement, wave function renormalization, and topological order". Phys. Rev. B. 82 (15): 155138. arXiv:1004.3835. Bibcode:2010PhRvB..82o5138C. doi:10.1103/physrevb.82.155138.
- ↑ Kohlstedt, K.L.; Vernizzi, G.; Solis, F.J.; Olvera de la Cruz, M. (2007). "Spontaneous Chirality via Long-range Electrostatic Forces". Physical Review Letters. 99 (3): 030602. arXiv:0704.3435. Bibcode:2007PhRvL..99c0602K. doi:10.1103/PhysRevLett.99.030602. PMID 17678276.
- ↑ "Minimal dynamical symmetry breaking of the standard model". Physical Review D. 41 (5): 1647–1660. 1990. Bibcode:1990PhRvD..41.1647B. doi:10.1103/PhysRevD.41.1647. PMID 10012522.
- ↑ The Nobel Foundation. "The Nobel Prize in Physics 2008". nobelprize.org. Retrieved January 15, 2008.
外部链接
- For a pedagogic introduction to electroweak symmetry breaking with step by step derivations, not found in texts, of many key relations, see http://www.quantumfieldtheory.info/Electroweak_Sym_breaking.pdf
- Spontaneous symmetry breaking
- Physical Review Letters – 50th Anniversary Milestone Papers
- In CERN Courier, Steven Weinberg reflects on spontaneous symmetry breaking
- Englert–Brout–Higgs–Guralnik–Hagen–Kibble Mechanism on Scholarpedia
- History of Englert–Brout–Higgs–Guralnik–Hagen–Kibble Mechanism on Scholarpedia
- The History of the Guralnik, Hagen and Kibble development of the Theory of Spontaneous Symmetry Breaking and Gauge Particles
- International Journal of Modern Physics A: The History of the Guralnik, Hagen and Kibble development of the Theory of Spontaneous Symmetry Breaking and Gauge Particles
- Guralnik, G S; Hagen, C R and Kibble, T W B (1967). Broken Symmetries and the Goldstone Theorem. Advances in Physics, vol. 2 Interscience Publishers, New York. pp. 567–708
- Spontaneous Symmetry Breaking in Gauge Theories: a Historical Survey
编者推荐
集智文章传递
多者异也:破缺的对称性与科学层级结构的本质 | 经典回顾
诺贝尔物理学奖得主、著名凝聚态物理学家菲利普·安德森(Philip Anderson,1923-),于1972年在Science发表了题为“More is Different”的论文。安德森通过介绍在各个尺度的物理系统都普遍存在的“对称性”和对称性破缺,对“还原论”思想提出了深刻的质疑。我们对这篇论文做了全文翻译,供读者参考。
对称性与拓扑序:新型量子计算机的物理基础
在过去的三十年里,凝聚态物理学家发现了物质的相的崭新领域:相互作用的粒子涌现的集体态(emergent, collective states)。这些新的物质状态迥异于通常的固态、液态或气态。这些物相有些已经在实验室中实现,而另一些只是理论上可能存在。
上世纪80年代关于分数量子霍尔效应(fractional quantum Hall effect)的实验表明,在某些情况下,电子大量分裂成分数粒子(fractions of particles),在时空中留下发辫般的轨迹。在另一些情况下,电子可以是零质量的集体激发。比如,自旋粒子的晶格变成旋转的环、分叉的弦的流体,再者,原本处于绝缘状态的晶体,表面开始导电,即拓扑绝缘体。
如今,为了发展量子计算机,微软和其他机构的研究小组正竞相将量子信息编码进这些发辫状与环状的物相。
同时,就在最近,凝聚态物理学家在理解可能产生的不同集体行为背后的模式方面取得了重大进展,目的是列举和分类所有可能的物相。如果实现了完整的分类,不仅可以解释到目前为止自然界中已知的所有物相,而且还可能指引新材料和新技术的方向。
在众多理论物理学家的带领下,加上数学家的贡献,研究人员已将大量一维或二维空间可能出现的物相分类,方法是将物质与其拓扑结构联系起来。(拓扑,即描述球面、环面等形状不变性的数学。)
其他文章
如何结合简单的的例子解释「对称性破缺」?
作者用在吃饭之前用左手还是右手拿筷子、墨西哥帽子等简单的例子解释了什么是对称性破缺。
本中文词条由趣木木参与编译,Fernando、西瓜、Jxzhou审校,糖糖编辑,如有问题,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。