“度 Degree”的版本间的差异

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
跳到导航 跳到搜索
 
第1行： 第1行：
−
此词条暂由彩云小译翻译，未经人工整理和审校，带来阅读不便，请见谅。
+
本词条由Ryan初步翻译
−
 
 
−
[[File:UndirectedDegrees (Loop).svg|thumb|A graph with a loop having vertices labeled by degree]]
 
−
 
 
−
A graph with a loop having vertices labeled by degree
 
−
 
 
−
有顶点按度标记的圈的图
 
  
 +
[[File:UndirectedDegrees (Loop).svg|thumb|
 +
图1：A graph with a loop having vertices labeled by degree 内含自环按度标记的图]]
  
  
第13行： 第9行：
 
In graph theory, the degree (or valency) of a vertex of a graph is the number of edges that are incident to the vertex, and in a multigraph, loops are counted twice. The degree of a vertex <math>v</math> is denoted <math>\deg(v)</math> or <math>\deg v</math>. The maximum degree of a graph <math>G</math>, denoted by <math>\Delta(G)</math>, and the minimum degree of a graph, denoted by <math>\delta(G)</math>, are the maximum and minimum degree of its vertices. In the multigraph on the right, the maximum degree is 5 and the minimum degree is 0.
 
In graph theory, the degree (or valency) of a vertex of a graph is the number of edges that are incident to the vertex, and in a multigraph, loops are counted twice. The degree of a vertex <math>v</math> is denoted <math>\deg(v)</math> or <math>\deg v</math>. The maximum degree of a graph <math>G</math>, denoted by <math>\Delta(G)</math>, and the minimum degree of a graph, denoted by <math>\delta(G)</math>, are the maximum and minimum degree of its vertices. In the multigraph on the right, the maximum degree is 5 and the minimum degree is 0.
  
−
在图论中，一个图的顶点的度(或价)是关联到该顶点的边的数量，在多重图中，循环被计数两次。顶点的度数表示“ math”或“ math”。图 < math > g </math > 的最大度，用 < math > Delta (g) </math > 表示; 图的最小度，用 < math > Delta (g) </math > 表示，是其顶点的最大度和最小度。在右多重图中，最大度为5，最小度为0。
+
在图论中，图中顶点的度(或价)是入射到该顶点的边的数量。在多重图中，自环会被计算两次。顶点的度数可表示为<math>\deg(v)</math>或<math>\deg v</math>。一个图<math>G</math>的最大度值表示为 < math > Delta (g) </math > ，最小度值表示为 <math>\delta(G)</math>。在右侧的多重图中，最大度值为5，最小度值为0。
  
  
第21行： 第17行：
 
In a regular graph, every vertex has the same degree, and so we can speak of the degree of the graph. A complete graph (denoted <math>K_n</math>, where <math>n</math> is the number of vertices in the graph) is a special kind of regular graph where all vertices have the maximum degree, <math>n-1</math>.
 
In a regular graph, every vertex has the same degree, and so we can speak of the degree of the graph. A complete graph (denoted <math>K_n</math>, where <math>n</math> is the number of vertices in the graph) is a special kind of regular graph where all vertices have the maximum degree, <math>n-1</math>.
  
−
在正则图中，每个顶点都具有相同的度，因此我们可以称之为图的度。一个完全图(表示“ math” > k _ n </math > ，其中 < math > n </math > 是图中顶点的数目)是一种特殊的正则图，其中所有顶点都有最大度，< math > n-1 </math > 。
+
在正则图中，每个顶点都具有相同的度值，因此我们可以称之为该图的度值。一个完全图(表示为<math>K_n</math>，其中<math>n</math>是图中顶点的数目)是一种特殊的正则图，其中所有顶点都有最大度值，<math>n-1</math>。
  
  
  
 
==Handshaking lemma==
 
==Handshaking lemma==
−
 
+
握手引理
 
{{main|Handshaking lemma}}
 
{{main|Handshaking lemma}}
  
第33行： 第29行：
 
The degree sum formula states that, given a graph <math>G=(V, E)</math>,
 
The degree sum formula states that, given a graph <math>G=(V, E)</math>,
  
−
度和公式表明，给定一个图 < math > g = (v，e) </math > ,
+
度和公式表明，给定一个图<math>G=(V, E)</math>,
  
  
第47行： 第43行：
 
The formula implies that in any undirected graph, the number of vertices with odd degree is even. This statement (as well as the degree  sum formula) is known as the [[handshaking lemma]]. The latter name comes from a popular mathematical problem, to prove that in any group of people the number of people who have shaken hands with an odd number of other people from the group is even.
 
The formula implies that in any undirected graph, the number of vertices with odd degree is even. This statement (as well as the degree  sum formula) is known as the [[handshaking lemma]]. The latter name comes from a popular mathematical problem, to prove that in any group of people the number of people who have shaken hands with an odd number of other people from the group is even.
  
−
The formula implies that in any undirected graph, the number of vertices with odd degree is even. This statement (as well as the degree sum formula) is known as the handshaking lemma. The latter name comes from a popular mathematical problem, to prove that in any group of people the number of people who have shaken hands with an odd number of other people from the group is even.
+
The formula implies that in any undirected graph, the number of vertices with odd degree is even. This statement (as well as the degree sum formula) is known as the handshaking lemma. The latter name comes from a popular mathematical problem, to prove that in any group of people the number of people who have shaken hands with an odd number of other people from the group is even.
  
−
该公式表明，在任何无向图中，奇次顶点的个数是偶数。这个语句(以及度和公式)被称为握手引理。后一个名字来自一个流行的数学问题，证明在任何人群中，与奇数人握过手的人数是偶数。
+
该公式表明，在任何无向图中，拥有奇数度值的顶点的个数是偶数。这个陈述(以及度和公式)被称为握手引理。该名字来自一个著名的数学问题，即证明无论该群体内有多少人，与奇数人握过手的人数是偶数。
  
  
  
 
==Degree sequence==
 
==Degree sequence==
 +
度序列
 +
[[File:Conjugate-dessins.svg|thumb|200px|
 +
图2：Two non-isomorphic graphs with the same degree sequence (3, 2, 2, 2, 2, 1, 1, 1).]]
  
−
[[File:Conjugate-dessins.svg|thumb|200px|Two non-isomorphic graphs with the same degree sequence (3, 2, 2, 2, 2, 1, 1, 1).]]
 
−
 
−
Two non-isomorphic graphs with the same degree sequence (3, 2, 2, 2, 2, 1, 1, 1).
 
−
 
−
具有相同度数列(3,2,2,2,2,2,1,1)的两个不同构图。
 
  
 
The '''degree sequence''' of an undirected graph is the non-increasing sequence of its vertex degrees;<ref>Diestel p.216</ref> for the above graph it is (5, 3, 3, 2, 2, 1, 0). The degree sequence is a [[graph invariant]] so [[Graph isomorphism|isomorphic graphs]] have the same degree sequence. However, the degree sequence does not, in general, uniquely identify a graph; in some cases, non-isomorphic graphs have the same degree sequence.
 
The '''degree sequence''' of an undirected graph is the non-increasing sequence of its vertex degrees;<ref>Diestel p.216</ref> for the above graph it is (5, 3, 3, 2, 2, 1, 0). The degree sequence is a [[graph invariant]] so [[Graph isomorphism|isomorphic graphs]] have the same degree sequence. However, the degree sequence does not, in general, uniquely identify a graph; in some cases, non-isomorphic graphs have the same degree sequence.
第65行： 第59行：
 
The degree sequence of an undirected graph is the non-increasing sequence of its vertex degrees; for the above graph it is (5, 3, 3, 2, 2, 1, 0). The degree sequence is a graph invariant so isomorphic graphs have the same degree sequence. However, the degree sequence does not, in general, uniquely identify a graph; in some cases, non-isomorphic graphs have the same degree sequence.
 
The degree sequence of an undirected graph is the non-increasing sequence of its vertex degrees; for the above graph it is (5, 3, 3, 2, 2, 1, 0). The degree sequence is a graph invariant so isomorphic graphs have the same degree sequence. However, the degree sequence does not, in general, uniquely identify a graph; in some cases, non-isomorphic graphs have the same degree sequence.
  
−
无向图的度序列是其顶点度的非递增序列，对于上述图是(5,3,3,2,2,1,0)。度序列是图的不变量，因此同构图具有相同的度序列。然而，度序列通常不能唯一地标识一个图，在某些情况下，不同构图具有相同的度序列。
+
无向图的度序列是指将其各顶点度值按非递增方式排序，对于上述图是(5,3,3,2,2,1,0)。度序列是图的不变量，因此同构图（两个图中顶点的度值都相同，但形状不同）具有相同的度序列。然而，度序列通常不能唯一地标识一个图，在某些情况下，非同构图具有相同的度序列。
  
  
第73行： 第67行：
 
The degree sequence problem  is the problem of finding some or all graphs with the degree sequence being a given non-increasing sequence of positive integers. (Trailing zeroes may be ignored since they are trivially realized by adding an appropriate number of isolated vertices to the graph.) A sequence which is the degree sequence of some graph, i.e. for which the degree sequence problem has a solution, is called a graphic or graphical sequence. As a consequence of the degree sum formula, any sequence with an odd sum, such as (3,&nbsp;3,&nbsp;1), cannot be realized as the degree sequence of a graph. The converse is also true: if a sequence has an even sum, it is the degree sequence of a multigraph. The construction of such a graph is straightforward: connect vertices with odd degrees in pairs by a matching, and fill out the remaining even degree counts by self-loops.
 
The degree sequence problem  is the problem of finding some or all graphs with the degree sequence being a given non-increasing sequence of positive integers. (Trailing zeroes may be ignored since they are trivially realized by adding an appropriate number of isolated vertices to the graph.) A sequence which is the degree sequence of some graph, i.e. for which the degree sequence problem has a solution, is called a graphic or graphical sequence. As a consequence of the degree sum formula, any sequence with an odd sum, such as (3,&nbsp;3,&nbsp;1), cannot be realized as the degree sequence of a graph. The converse is also true: if a sequence has an even sum, it is the degree sequence of a multigraph. The construction of such a graph is straightforward: connect vertices with odd degrees in pairs by a matching, and fill out the remaining even degree counts by self-loops.
  
−
度序列问题是寻找度序列为给定的正整数非增序列的部分或全部图的问题。(拖尾的零可能被忽略，因为它们通过向图中添加适当数量的孤立顶点来实现。)一个序列是某个图的度序列，即。度序列问题有解决方案的，称为图形序列或图形序列。由于度和公式的结果，任何具有奇数和的序列，如(3,3,1) ，都不能实现为图的度序列。反之亦然: 如果一个序列有偶数和，它就是重图的度序列。这样一个图的构造很简单: 通过匹配将奇数度数的顶点成对连接起来，然后通过自循环填充剩余的偶数度数。
+
度序列问题，是指寻找具有以非增方式排列给定正整数的度序列的局部或全部图的问题。(序列尾部的零可能会被忽略，因为通过向图中添加适当数量的孤立顶点就可以轻松实现序列尾部不断加零。)一个序列是某个图的度序列，即一个度序列问题有解时，该序列称为图形序列。由于度和公式的存在，任何具有奇数和的序列，如(3,3,1) ，都不会是图的度序列。反之亦然: 如果一个序列有偶数和，它就是重图的度序列。构造这样一个图是很简单: 通过匹配将奇数度值的顶点成对连接起来，然后剩余的偶数度值顶点都连出一条边指向自己。
  
 
The question of whether a given degree sequence can be realized by a [[simple graph]] is more challenging. This problem is also called [[graph realization problem]] and can either be solved by the [[Erdős–Gallai theorem]] or the [[Havel–Hakimi algorithm]].  
 
The question of whether a given degree sequence can be realized by a [[simple graph]] is more challenging. This problem is also called [[graph realization problem]] and can either be solved by the [[Erdős–Gallai theorem]] or the [[Havel–Hakimi algorithm]].  
第79行： 第73行：
 
The question of whether a given degree sequence can be realized by a simple graph is more challenging. This problem is also called graph realization problem and can either be solved by the Erdős–Gallai theorem or the Havel–Hakimi algorithm.  
 
The question of whether a given degree sequence can be realized by a simple graph is more challenging. This problem is also called graph realization problem and can either be solved by the Erdős–Gallai theorem or the Havel–Hakimi algorithm.  
  
−
一个给定的度序列是否可以用一个简单的图来实现的问题更具有挑战性。这个问题也称为图实现问题，既可以用 erd s-Gallai 定理解决，也可以用 Havel-Hakimi 算法解决。
+
一个给定的度序列是否可以用一个简单的图进行表示，是一个具有挑战性的问题。这个问题也称为图实现问题，可以用 Erdős–Gallai定理解决，也可以用Havel-Hakimi算法解决。
  
 
The problem of finding or estimating the  number of graphs with a given degree sequence is a problem from the field of [[graph enumeration]].
 
The problem of finding or estimating the  number of graphs with a given degree sequence is a problem from the field of [[graph enumeration]].
第85行： 第79行：
 
The problem of finding or estimating the  number of graphs with a given degree sequence is a problem from the field of graph enumeration.
 
The problem of finding or estimating the  number of graphs with a given degree sequence is a problem from the field of graph enumeration.
  
−
寻找或估计具有给定度序列的图的个数问题是图计数领域中的一个问题。
+
基于给定度序列寻找或估计可能的图的个数，是图枚举领域中的一个问题。
  
  
第93行： 第87行：
 
More generally, the degree sequence of a hypergraph is the non-increasing sequence of its vertex degrees. A sequence is <math>k</math>-graphic if it is the degree sequence of some <math>k</math>-uniform hypergraph. In particular, a <math>2</math>-graphic sequence is graphic. Deciding if a given sequence is <math>k</math>-graphic is doable in polynomial time for <math>k=2</math> via the Erdős–Gallai theorem but is NP-complete for all <math>k\ge 3</math> (Deza et al., 2018 ).
 
More generally, the degree sequence of a hypergraph is the non-increasing sequence of its vertex degrees. A sequence is <math>k</math>-graphic if it is the degree sequence of some <math>k</math>-uniform hypergraph. In particular, a <math>2</math>-graphic sequence is graphic. Deciding if a given sequence is <math>k</math>-graphic is doable in polynomial time for <math>k=2</math> via the Erdős–Gallai theorem but is NP-complete for all <math>k\ge 3</math> (Deza et al., 2018 ).
  
−
一般来说，超图的度序列是其顶点度的非递增序列。一个序列是 < math > k </math >-graphic，如果它是一些 < math > k </math >-uniform 超图的度序列。特别是 < math > 2 </math >-graphic 序列是图形。决定一个给定的序列是否是 < math > k </math >-graphic 可以在多项式时间内通过 erd s-Gallai 定理实现 < math > k = 2 </math > ，但是对于所有 < math > k ge 3 </math > 是 np 完全的(Deza et al. ，2018)。
+
一般来说，超图的度序列是其顶点度的非递增序列。一个序列是<math>k</math>-graphic，如果它是一些<math>k</math>-uniform超图的度序列。特别是 < math > 2 </math >-graphic 序列是图形。决定一个给定的序列是否是 < math > k </math >-graphic 可以在 < math > k = 2 </math >的多项式时间内通过Erdős–Gallai定理实现，但是当<math>k\ge 3</math>时该问题转化为NP完全问题(Deza et al. ，2018)。
  
  
  
 
==Special values==
 
==Special values==
−
 
+
特殊值
−
[[File:Depth-first-tree.png|thumb|An undirected graph with leaf nodes 4, 5, 6, 7, 10, 11, and 12]]
+
[[File:Depth-first-tree.png|thumb|
−
 
+
图3：An undirected graph with leaf nodes 4, 5, 6, 7, 10, 11, and 12 一个具有叶节点的无定向图]]
−
An undirected graph with leaf nodes 4, 5, 6, 7, 10, 11, and 12
 
−
 
 
−
具有叶节点4、5、6、7、10、11和12的无向图
 
  
 
*A vertex with degree 0 is called an [[isolated vertex]].
 
*A vertex with degree 0 is called an [[isolated vertex]].
−
 
+
度值为0的顶点成为孤立顶点
 
*A vertex with degree 1 is called a leaf vertex or end vertex, and the edge incident with that vertex is called a pendant edge. In the graph on the right, {3,5} is a pendant edge. This terminology is common in the study of [[tree (graph theory)|tree]]s in graph theory and especially [[tree (data structure)|tree]]s as [[data structure]]s.
 
*A vertex with degree 1 is called a leaf vertex or end vertex, and the edge incident with that vertex is called a pendant edge. In the graph on the right, {3,5} is a pendant edge. This terminology is common in the study of [[tree (graph theory)|tree]]s in graph theory and especially [[tree (data structure)|tree]]s as [[data structure]]s.
−
 
+
度值为1的顶点称为叶顶点或尾顶点，该顶点的入射边称为悬挂边。在右侧的图中，{3,5}就是一个悬挂边。在图论中，该术语主要在研究树时使用，特别是具有树形结构的数据。
 
* A vertex with degree ''n''&nbsp;&minus;&nbsp;1  in a graph on ''n'' vertices is called a [[dominating vertex]].
 
* A vertex with degree ''n''&nbsp;&minus;&nbsp;1  in a graph on ''n'' vertices is called a [[dominating vertex]].
−
 
+
在有n个顶点的图中，度值为n-1的顶点叫作主导顶点
  
  
 
==Global properties==
 
==Global properties==
−
 
+
全局属性
 
*If each vertex of the graph has the same degree&nbsp;''k'' the graph is called a [[regular graph|''k''-regular graph]] and the graph itself is said to have degree&nbsp;''k''. Similarly, a [[bipartite graph]] in which every two vertices on the same side of the bipartition as each other have the same degree is called a [[biregular graph]].
 
*If each vertex of the graph has the same degree&nbsp;''k'' the graph is called a [[regular graph|''k''-regular graph]] and the graph itself is said to have degree&nbsp;''k''. Similarly, a [[bipartite graph]] in which every two vertices on the same side of the bipartition as each other have the same degree is called a [[biregular graph]].
−
 
+
如果一个图中的所有顶点的度值都为k，该图被称为k-正则图，该图的度值也为k。相似的，同侧每两个顶点都具有相同度值的二分图叫作二分正则图。
 
*An undirected, connected graph has an [[Eulerian path]] if and only if it has either 0 or 2 vertices of odd degree. If it has 0 vertices of odd degree, the Eulerian path is an Eulerian circuit.
 
*An undirected, connected graph has an [[Eulerian path]] if and only if it has either 0 or 2 vertices of odd degree. If it has 0 vertices of odd degree, the Eulerian path is an Eulerian circuit.
−
 
+
当且仅当具有0或2个奇数度的顶点时，无向连通图才具有欧拉路径。 如果它具有0个奇数度的顶点，则欧拉路径为欧拉回路。
 
*A directed graph is a [[pseudoforest]] if and only if every vertex has outdegree at most&nbsp;1. A [[functional graph]] is a special case of a pseudoforest in which every vertex has outdegree exactly&nbsp;1.
 
*A directed graph is a [[pseudoforest]] if and only if every vertex has outdegree at most&nbsp;1. A [[functional graph]] is a special case of a pseudoforest in which every vertex has outdegree exactly&nbsp;1.
−
 
+
有向图是当且仅当每个顶点的度值最大为1时才是伪森林。功能图是伪森林的特例，其中每个顶点的度数都恰好为1。
 
*By [[Brooks' theorem]], any graph other than a clique or an odd cycle has [[chromatic number]] at most&nbsp;Δ, and by [[Vizing's theorem]] any graph has [[chromatic index]] at most Δ&nbsp;+&nbsp;1.
 
*By [[Brooks' theorem]], any graph other than a clique or an odd cycle has [[chromatic number]] at most&nbsp;Δ, and by [[Vizing's theorem]] any graph has [[chromatic index]] at most Δ&nbsp;+&nbsp;1.
−
 
+
根据布鲁克斯定理，除团簇或奇数循环外，任何图的色度数最大为Δ，而根据维辛定理，任何图的色度指数最大为Δ+ 1。
 
*A [[Degeneracy (graph theory)|''k''-degenerate graph]] is a graph in which each subgraph has a vertex of degree at most ''k''.
 
*A [[Degeneracy (graph theory)|''k''-degenerate graph]] is a graph in which each subgraph has a vertex of degree at most ''k''.
−
 
+
k简并图是其中每个子图最多具有度值为k的顶点的图。
  
  
第130行： 第121行：
  
 
*[[Indegree]], [[outdegree]] for [[digraph (mathematics)|digraph]]s
 
*[[Indegree]], [[outdegree]] for [[digraph (mathematics)|digraph]]s
−
 
+
有向图的入度和出度
 
*[[Degree distribution]]
 
*[[Degree distribution]]
−
 
+
度分布
 
*[[bipartite graph|degree sequence]] for bipartite graphs
 
*[[bipartite graph|degree sequence]] for bipartite graphs
−
 
+
二分图的度序列
  
  

2020年8月15日 (六) 17:16的版本

本词条由Ryan初步翻译

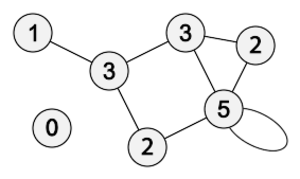
图1：A graph with a loop having vertices labeled by degree 内含自环按度标记的图


In graph theory, the degree (or valency) of a vertex of a graph is the number of edges that are incident to the vertex, and in a multigraph, loops are counted twice.[1] The degree of a vertex [math]\displaystyle{ v }[/math] is denoted [math]\displaystyle{ \deg(v) }[/math] or [math]\displaystyle{ \deg v }[/math]. The maximum degree of a graph [math]\displaystyle{ G }[/math], denoted by [math]\displaystyle{ \Delta(G) }[/math], and the minimum degree of a graph, denoted by [math]\displaystyle{ \delta(G) }[/math], are the maximum and minimum degree of its vertices. In the multigraph on the right, the maximum degree is 5 and the minimum degree is 0.

In graph theory, the degree (or valency) of a vertex of a graph is the number of edges that are incident to the vertex, and in a multigraph, loops are counted twice. The degree of a vertex [math]\displaystyle{ v }[/math] is denoted [math]\displaystyle{ \deg(v) }[/math] or [math]\displaystyle{ \deg v }[/math]. The maximum degree of a graph [math]\displaystyle{ G }[/math], denoted by [math]\displaystyle{ \Delta(G) }[/math], and the minimum degree of a graph, denoted by [math]\displaystyle{ \delta(G) }[/math], are the maximum and minimum degree of its vertices. In the multigraph on the right, the maximum degree is 5 and the minimum degree is 0.

在图论中，图中顶点的度(或价)是入射到该顶点的边的数量。在多重图中，自环会被计算两次。顶点的度数可表示为[math]\displaystyle{ \deg(v) }[/math]或[math]\displaystyle{ \deg v }[/math]。一个图[math]\displaystyle{ G }[/math]的最大度值表示为 < math > Delta (g) </math > ，最小度值表示为 [math]\displaystyle{ \delta(G) }[/math]。在右侧的多重图中，最大度值为5，最小度值为0。


In a regular graph, every vertex has the same degree, and so we can speak of the degree of the graph. A complete graph (denoted [math]\displaystyle{ K_n }[/math], where [math]\displaystyle{ n }[/math] is the number of vertices in the graph) is a special kind of regular graph where all vertices have the maximum degree, [math]\displaystyle{ n-1 }[/math].

In a regular graph, every vertex has the same degree, and so we can speak of the degree of the graph. A complete graph (denoted [math]\displaystyle{ K_n }[/math], where [math]\displaystyle{ n }[/math] is the number of vertices in the graph) is a special kind of regular graph where all vertices have the maximum degree, [math]\displaystyle{ n-1 }[/math].

在正则图中，每个顶点都具有相同的度值，因此我们可以称之为该图的度值。一个完全图(表示为[math]\displaystyle{ K_n }[/math]，其中[math]\displaystyle{ n }[/math]是图中顶点的数目)是一种特殊的正则图，其中所有顶点都有最大度值，[math]\displaystyle{ n-1 }[/math]。


Handshaking lemma

握手引理

Main article: Handshaking lemma

The degree sum formula states that, given a graph [math]\displaystyle{ G=(V, E) }[/math],

The degree sum formula states that, given a graph [math]\displaystyle{ G=(V, E) }[/math],

度和公式表明，给定一个图[math]\displaystyle{ G=(V, E) }[/math],


[math]\displaystyle{ \sum_{v \in V} \deg(v) = 2|E|\, . }[/math]

[math]\displaystyle{ \sum_{v \in V} \deg(v) = 2|E|\, . }[/math]

[math]\displaystyle{ \sum_{v \in V} \deg(v) = 2|E|\, . }[/math]


The formula implies that in any undirected graph, the number of vertices with odd degree is even. This statement (as well as the degree sum formula) is known as the handshaking lemma. The latter name comes from a popular mathematical problem, to prove that in any group of people the number of people who have shaken hands with an odd number of other people from the group is even.

The formula implies that in any undirected graph, the number of vertices with odd degree is even. This statement (as well as the degree sum formula) is known as the handshaking lemma. The latter name comes from a popular mathematical problem, to prove that in any group of people the number of people who have shaken hands with an odd number of other people from the group is even.

该公式表明，在任何无向图中，拥有奇数度值的顶点的个数是偶数。这个陈述(以及度和公式)被称为握手引理。该名字来自一个著名的数学问题，即证明无论该群体内有多少人，与奇数人握过手的人数是偶数。


Degree sequence

度序列

图2：Two non-isomorphic graphs with the same degree sequence (3, 2, 2, 2, 2, 1, 1, 1).


The degree sequence of an undirected graph is the non-increasing sequence of its vertex degrees;[2] for the above graph it is (5, 3, 3, 2, 2, 1, 0). The degree sequence is a graph invariant so isomorphic graphs have the same degree sequence. However, the degree sequence does not, in general, uniquely identify a graph; in some cases, non-isomorphic graphs have the same degree sequence.

The degree sequence of an undirected graph is the non-increasing sequence of its vertex degrees; for the above graph it is (5, 3, 3, 2, 2, 1, 0). The degree sequence is a graph invariant so isomorphic graphs have the same degree sequence. However, the degree sequence does not, in general, uniquely identify a graph; in some cases, non-isomorphic graphs have the same degree sequence.

无向图的度序列是指将其各顶点度值按非递增方式排序，对于上述图是(5,3,3,2,2,1,0)。度序列是图的不变量，因此同构图（两个图中顶点的度值都相同，但形状不同）具有相同的度序列。然而，度序列通常不能唯一地标识一个图，在某些情况下，非同构图具有相同的度序列。


The degree sequence problem is the problem of finding some or all graphs with the degree sequence being a given non-increasing sequence of positive integers. (Trailing zeroes may be ignored since they are trivially realized by adding an appropriate number of isolated vertices to the graph.) A sequence which is the degree sequence of some graph, i.e. for which the degree sequence problem has a solution, is called a graphic or graphical sequence. As a consequence of the degree sum formula, any sequence with an odd sum, such as (3, 3, 1), cannot be realized as the degree sequence of a graph. The converse is also true: if a sequence has an even sum, it is the degree sequence of a multigraph. The construction of such a graph is straightforward: connect vertices with odd degrees in pairs by a matching, and fill out the remaining even degree counts by self-loops.

The degree sequence problem is the problem of finding some or all graphs with the degree sequence being a given non-increasing sequence of positive integers. (Trailing zeroes may be ignored since they are trivially realized by adding an appropriate number of isolated vertices to the graph.) A sequence which is the degree sequence of some graph, i.e. for which the degree sequence problem has a solution, is called a graphic or graphical sequence. As a consequence of the degree sum formula, any sequence with an odd sum, such as (3, 3, 1), cannot be realized as the degree sequence of a graph. The converse is also true: if a sequence has an even sum, it is the degree sequence of a multigraph. The construction of such a graph is straightforward: connect vertices with odd degrees in pairs by a matching, and fill out the remaining even degree counts by self-loops.

度序列问题，是指寻找具有以非增方式排列给定正整数的度序列的局部或全部图的问题。(序列尾部的零可能会被忽略，因为通过向图中添加适当数量的孤立顶点就可以轻松实现序列尾部不断加零。)一个序列是某个图的度序列，即一个度序列问题有解时，该序列称为图形序列。由于度和公式的存在，任何具有奇数和的序列，如(3,3,1) ，都不会是图的度序列。反之亦然: 如果一个序列有偶数和，它就是重图的度序列。构造这样一个图是很简单: 通过匹配将奇数度值的顶点成对连接起来，然后剩余的偶数度值顶点都连出一条边指向自己。

The question of whether a given degree sequence can be realized by a simple graph is more challenging. This problem is also called graph realization problem and can either be solved by the Erdős–Gallai theorem or the Havel–Hakimi algorithm.

The question of whether a given degree sequence can be realized by a simple graph is more challenging. This problem is also called graph realization problem and can either be solved by the Erdős–Gallai theorem or the Havel–Hakimi algorithm.

一个给定的度序列是否可以用一个简单的图进行表示，是一个具有挑战性的问题。这个问题也称为图实现问题，可以用 Erdős–Gallai定理解决，也可以用Havel-Hakimi算法解决。

The problem of finding or estimating the number of graphs with a given degree sequence is a problem from the field of graph enumeration.

The problem of finding or estimating the number of graphs with a given degree sequence is a problem from the field of graph enumeration.

基于给定度序列寻找或估计可能的图的个数，是图枚举领域中的一个问题。


More generally, the degree sequence of a hypergraph is the non-increasing sequence of its vertex degrees. A sequence is [math]\displaystyle{ k }[/math]-graphic if it is the degree sequence of some [math]\displaystyle{ k }[/math]-uniform hypergraph. In particular, a [math]\displaystyle{ 2 }[/math]-graphic sequence is graphic. Deciding if a given sequence is [math]\displaystyle{ k }[/math]-graphic is doable in polynomial time for [math]\displaystyle{ k=2 }[/math] via the Erdős–Gallai theorem but is NP-complete for all [math]\displaystyle{ k\ge 3 }[/math] (Deza et al., 2018 [3]).

More generally, the degree sequence of a hypergraph is the non-increasing sequence of its vertex degrees. A sequence is [math]\displaystyle{ k }[/math]-graphic if it is the degree sequence of some [math]\displaystyle{ k }[/math]-uniform hypergraph. In particular, a [math]\displaystyle{ 2 }[/math]-graphic sequence is graphic. Deciding if a given sequence is [math]\displaystyle{ k }[/math]-graphic is doable in polynomial time for [math]\displaystyle{ k=2 }[/math] via the Erdős–Gallai theorem but is NP-complete for all [math]\displaystyle{ k\ge 3 }[/math] (Deza et al., 2018 ).

一般来说，超图的度序列是其顶点度的非递增序列。一个序列是[math]\displaystyle{ k }[/math]-graphic，如果它是一些[math]\displaystyle{ k }[/math]-uniform超图的度序列。特别是 < math > 2 </math >-graphic 序列是图形。决定一个给定的序列是否是 < math > k </math >-graphic 可以在 < math > k = 2 </math >的多项式时间内通过Erdős–Gallai定理实现，但是当[math]\displaystyle{ k\ge 3 }[/math]时该问题转化为NP完全问题(Deza et al. ，2018)。


Special values

特殊值

图3：An undirected graph with leaf nodes 4, 5, 6, 7, 10, 11, and 12 一个具有叶节点的无定向图

度值为0的顶点成为孤立顶点

  • A vertex with degree 1 is called a leaf vertex or end vertex, and the edge incident with that vertex is called a pendant edge. In the graph on the right, {3,5} is a pendant edge. This terminology is common in the study of trees in graph theory and especially trees as data structures.

度值为1的顶点称为叶顶点或尾顶点，该顶点的入射边称为悬挂边。在右侧的图中，{3,5}就是一个悬挂边。在图论中，该术语主要在研究树时使用，特别是具有树形结构的数据。

  • A vertex with degree n − 1 in a graph on n vertices is called a dominating vertex.

在有n个顶点的图中，度值为n-1的顶点叫作主导顶点


Global properties

全局属性

  • If each vertex of the graph has the same degree k the graph is called a k-regular graph and the graph itself is said to have degree k. Similarly, a bipartite graph in which every two vertices on the same side of the bipartition as each other have the same degree is called a biregular graph.

如果一个图中的所有顶点的度值都为k，该图被称为k-正则图，该图的度值也为k。相似的，同侧每两个顶点都具有相同度值的二分图叫作二分正则图。

  • An undirected, connected graph has an Eulerian path if and only if it has either 0 or 2 vertices of odd degree. If it has 0 vertices of odd degree, the Eulerian path is an Eulerian circuit.

当且仅当具有0或2个奇数度的顶点时，无向连通图才具有欧拉路径。 如果它具有0个奇数度的顶点，则欧拉路径为欧拉回路。

  • A directed graph is a pseudoforest if and only if every vertex has outdegree at most 1. A functional graph is a special case of a pseudoforest in which every vertex has outdegree exactly 1.

有向图是当且仅当每个顶点的度值最大为1时才是伪森林。功能图是伪森林的特例，其中每个顶点的度数都恰好为1。

根据布鲁克斯定理，除团簇或奇数循环外，任何图的色度数最大为Δ，而根据维辛定理，任何图的色度指数最大为Δ+ 1。

k简并图是其中每个子图最多具有度值为k的顶点的图。


See also

有向图的入度和出度

度分布

二分图的度序列


Notes

  1. ↑ Diestel p.5
  2. ↑ Diestel p.216
  3. ↑ Deza, Antoine; Levin, Asaf; Meesum, Syed M.; Onn, Shmuel (January 2018). "Optimization over Degree Sequences". SIAM Journal on Discrete Mathematics (in English). 32 (3): 2067–2079. arXiv:1706.03951. doi:10.1137/17M1134482. ISSN 0895-4801.


References

1955年), [http://eudml.org/doc/19050

Http://eudml.org/doc/19050 "关于有限图存在性的一个注记"], Časopis pro pěstování matematiky (in Czech), 80

80: 477–480 {{citation}}: Check |url= value (help); Check date values in: |year= (help); Unknown parameter |页数= ignored (help); line feed character in |url= at position 27 (help); line feed character in |volume= at position 3 (help); line feed character in |year= at position 5 (help)CS1 maint: unrecognized language (link)

}}

}}

  • Hakimi, S.l. (1962), "一组整数作为线性图顶点度的可实现性。一", Journal of the Society for Industrial and Applied Mathematics 工业与应用数学学会杂志, 10

10: 496–506, MR [//www.ams.org/mathscinet-getitem?mr=0148049%0A%0A0148049%E5%85%88%E7%94%9F 0148049 0148049先生] {{citation}}: Check |mr= value (help); Unknown parameter |页数= ignored (help); line feed character in |journal= at position 62 (help); line feed character in |mr= at position 8 (help); line feed character in |volume= at position 3 (help). 

| year = 1962}}.

1962}}.

  • Sierksma, Gerard

1 = 杰拉德; Hoogeveen, Han (1991), "整数序列为图形的七个条件", Journal of Graph Theory, 15

15 (2

2): 223–231, doi:[//doi.org/10.1002%2Fjgt.3190150209%0A%0A10.1002%2Fjgt.%203190150209 10.1002/jgt.3190150209 10.1002/jgt. 3190150209], MR [//www.ams.org/mathscinet-getitem?mr=1106533%0A%0A1106533%E5%85%88%E7%94%9F 1106533 1106533先生] {{citation}}: Check |doi= value (help); Check |mr= value (help); Unknown parameter |Journal= ignored (|journal= suggested) (help); line feed character in |doi= at position 23 (help); line feed character in |first1= at position 7 (help); line feed character in |issue= at position 2 (help); line feed character in |mr= at position 8 (help); line feed character in |volume= at position 3 (help). 

| year = 1991}}.

1991}}.

Category:Graph theory

范畴: 图论


This page was moved from wikipedia:en:Degree (graph theory). Its edit history can be viewed at 度/edithistory

取自“https://wiki.swarma.org/index.php?title=度_Degree&oldid=12581”