无标度网络 Scale-free network
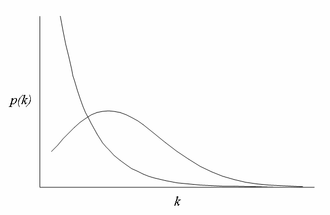
无标度网络 scale-free network是一种度分布(即对复杂网络中节点度数的总体描述)服从或者接近幂律分布的复杂网络。无标度网络中某节点与另外 [math]\displaystyle{ k }[/math] 个节点相连接(度数为 [math]\displaystyle{ k }[/math] )的概率是:
其中, [math]\displaystyle{ {\gamma} }[/math] 是一个通常位于2和3之间的参数,但偶尔也会在这个区间之外。[1][2]
许多网络似乎都体现出无标度的特性,然而统计分析却表明许多网络并不符合无标度特性。[3][4] 偏好依附 preferential attachment和适应度模型 fitness model是对现实中的网络如何产生幂律度分布的可能解释。
历史
在对科学引文网的研究中,普赖斯 Derek de Solla Price在1965年发现:论文的链接数,即该论文被引用的次数,服从厚尾的帕累托分布 Pareto distribution或者幂律分布,由此得出引文网络是无标度的。然而他当时并未使用“无标度网络”这个术语。这个术语直到几十年之后才出现。在1976年的论文中,普赖斯还提出了一种解释引文网络产生幂律分布的机制,他称之为“累积优势 cumulative advantage”,也就是现今更被熟知的“偏好依附 preferential attachment”。
近期对无标度网络的关注始于1999年圣母大学的艾伯特-拉斯洛·巴拉巴西 Albert-László Barabási 及其同事着手对部分万维网的拓扑结构进行绘制。[5]他们发现有些他们称之“枢纽 hubs”的节点比其他节点具有更多的链接数,同时网络任意节点的链接数服从幂律分布。在发现其他的网络,如部分社会网络和生物网络也具有厚尾的度分布之后,巴拉巴西及其同事创造了“无标度网络 Scale-free network”一词来描述这类度分布呈幂律的网络。Amaral等人指出,可以根据大k值的度分布的衰减,将大部分现实世界的网络归为两个大类。
巴拉巴西和艾伯特提出了一种他们称之为偏好依附 preferential attachment的生成机制,用来解释幂律分布,这基本上和普赖斯提出的机制相同。这种机制的解析解(也与普莱斯的相似)由Dorogovtsev,Mendes和Samukhin<>Dorogovtsev, S., Mendes, J., Samukhin, A. (2000) "Structure of Growing Networks with Preferential Linking".Physical Review Letters.85.21:(4633--4636)</ref>于2000年提出,Krapivsky,Redner和Leyvraz 等人也同时独立提出。后来由数学家贝拉·波洛巴斯 BélaBollobás严格证明。[6] 然而这种机制所生成的网络只是无标度网络这个大类中的特殊子集,许多其他机制自此也陆续被发现。[7]
无标度网络的历史还存有一部分争议。在实证层面上,许多网络的无标度性被质疑。如Faloutsos三兄弟认为互联网是基于网络层错觉,实则是体现为高度节点的ASes数据链结构。[8]
在理论层面上,研究者提出了对无标度的抽象定义的改良。例如李等人(2005)近日提供了更加准确的“无标度指标”。简而言之,定义 [math]\displaystyle{ G }[/math] 是具有连边集合E的图,顶点 [math]\displaystyle{ v }[/math] 的度(即与[math]\displaystyle{ v }[/math]邻接的边的数量)记为[math]\displaystyle{ deg\left ( v \right ) }[/math]。定义:
[math]\displaystyle{ s(G) }[/math]在高度节点与其他高度节点邻接时最大。定义:
其中,[math]\displaystyle{ {s}_{max} }[/math] 是所有与 [math]\displaystyle{ G }[/math] 的度分布相同的图的集合中图 [math]\displaystyle{ H }[/math] 的 [math]\displaystyle{ s(H) }[/math] 的最大值。 [math]\displaystyle{ S(G) }[/math] 是一个值域在0和1之间的指标,具有较小 [math]\displaystyle{ S(G) }[/math] 的图 [math]\displaystyle{ G }[/math] 是“丰标度”的,一个具有接近1的 [math]\displaystyle{ S(G) }[/math] 的图 [math]\displaystyle{ G }[/math] 是“无标度”的。这个定义体现了“无标度”所隐含的自相似性的概念。
特征
无标度网络的特性是普遍存在度远高于平均值的节点。度最高的节点通常称为枢纽 hub,被认为在网络中起到特殊作用,尽管这还要看具体在网络的哪个区域。
无标度性与网络应对失败的鲁棒性有很大关系。主要的枢纽节点通常连接着小的枢纽节点。这些小的枢纽节点再伴随着度更小的节点,以此类推。这种层级关系使得网络能够容错 fault tolerant行。如果错误随机发生,并且大量节点都具有较小的度,那么枢纽节点几乎不会受到影响。即便枢纽节点出现了错误,因为还有其他枢纽节点,网络通常不会失去原来的连通性 connectedness。然而,如果定向选择一些主要的枢纽节点并把它们从网络中去除,网络则会变为许多相对离散的图。因此,枢纽节点既是无标度网络的优势又是劣势。Cohen[9][10]和Callaway[11]等人曾用渗流理论 percolation theory分析过这些特性。 Cohen[12]证明对于大范围的无标度网络临界渗流阈值 critical percolation threshold, p_{c}=0.这表明从网络中随机删去任意数量的节点都不会破坏网络。这与 p_{c} =1/[math]\displaystyle{ \bar{k} }[/math]的Erdős–Rényi图形成了对比,其中 [math]\displaystyle{ \bar{k} }[/math] 是图的平均度。
无标度网络的另一个重要特性是随节点度数升高而降低的聚集系数 clustering coefficient分布。这个分布也服从幂律分布。这表明度数低的节点从属于致密的子图,这些子图再通过枢纽节点互相连接。试想一个社交网络,它的节点是人,而链接是熟人关系。很容易得出人们倾向于形成社群,也就是互相熟识的团体(可以将它理解为一个全连接图 complete graph )。另外这个小社群的人们也会有一些社群外的熟人关系。然而有些人与许多社群相连(如贵族、政治家)。这些人可以被认作是导致小世界现象 small-world phenomenon的缘由。
目前无标度网络的更具体的特性会根据他们不同的生成机制而改变。例如,由“偏好依附“生成的网络普遍将度较高的顶点放在网络的中央,将他们互相连接形成一个核心,由度逐渐降低的节点构成核心之间的区域以及外围。即便随机删除较大部分的顶点对网络整体的联通都不会有太大影响,这表明这种拓扑结构有利于提升安全性,尽管一些定向攻击会很快破坏其连通性。其他的一些将度较高的顶点放在外围的无标度网络并没有这样的性质。也就是说无标度网络的聚集系数会随着拓扑构造的改变而产生明显变化。
最后一个特性是关于网络中顶点之间的平均距离。对于大多数不规则网络,如小世界网络,这个距离相较于高度规则的网格图是非常小的。Cohen和Havlin证明了,2 < [math]\displaystyle{ {\gamma} }[/math] < 3的无关联幂律图会有非常小的半径[math]\displaystyle{ d\sim ln ln N }[/math]其中[math]\displaystyle{ N }[/math]是网络中节点的数量。[13] 在实践中,一个生长中的无标度网络的半径几乎可以被认作是一个定值。
随机图的特性在图变形的过程中可能会变化也可能不变。正如Mashaghi A.等人所展示的,在一个将随机图转变为其双边图(或者线图)的过程中会产生一系列度分布近似,却提升了度相关性并且显著提升了聚集系数的图。[14]
示例
尽管许多真实世界的网络被认为是无标度的,然而其证明却往往因为愈发严格的数据分析技术而显得不够充分。[3]由此,许多网络的无标度性还在科学社群中被讨论着。一些声称是无标度的网络包括:
• 社交网络包括合作网络。两个被广泛研究的示例是演员合演电影的合作网络和数学家合著论文的合作网络。
• 电脑网络包括互联网和万维网的网图。
• 蛋白质-蛋白质相互作用 Protein-protein interaction网络。
• 航空网络 Airline networks。
在高温超导体中也发现了无标度的拓扑结构。高温超导体[18]
——其中电子服从量子物理,能够完美同步,零电阻地流动——似乎与看似随机的氧原子和晶格畸变的分形排列有关。[19]
近日发现,一种填充空间的元胞结构,加权平面随机晶格的配位数分布服从幂律分布。这暗示着晶格有一小部分区块,与它们公用边界的邻居的数量惊人地多。其构造由一个类似于将单位面积的正方形随机分割为四个区块发生器引发。于是这个发生器不断地被可用区块中的一个吸引,这个区块是从对应区域中择优选取的。这个动作将正方形划分为更小的互斥矩形块。通过用区块中心处的节点替换每个区块,再把区块间的公共边界替换为连接对应顶点的边,从而获得的WPSL(DWPSL)的对偶形成了一个度分布呈幂律分布的网络。[20][21] 它按照中介驱动的依附模型 mediation-driven attachment model规则生成,这看上去也体现着偏好依附的规则。
构建模型
无标度网络的出现不仅仅是时运使然。Erdős和Rényi (1960)研究了一种在每一个步骤中均匀地随机选择两个节点然后在他们之间加入链接的图生成模型。这些随机图中的特性与无标度网络很不一样,因此需要一种生成过程的模型。
最被熟知的无标度网络子集的生成模型是Barabási和Albert(1999)的富者更富 rich get richer模型生成,它让每个网页根据一个非均匀的概率分布与既存网页建立连接,这个概率分布与当前网页的入度数成比例。这个模型最初由普赖斯在1965 年发明,并命名为累积优势,但是直到Barabási重新以现在的名字([BA模型])发现之后才开始受到关注的。根据这个过程,拥有更多入度的的网页相较一般网页会吸引更多的链接。这样的机制会产生幂律,但是这样的图和真实的网络图在其他特性上有所不同,例如没有紧密连接的小社群。人们开始提出和研究一些更加普适的模型和网络特性。例如Pachon(2018)等人提出了富者更富模型的一个变式,它考量了两种不同的依附规则:偏好依附和仅对最新节点的均匀选择。[22] 可以参考Dorogovtsev和Mendes的著作中对此的回顾。
Pennock等人对因特网链接提出了一个略有差别的生成模型。它们研究了对某一特定话题有兴趣的社群,如宇宙、上市公司、报纸或者科学家,并且弃用了因特网的一些主要枢纽。这个条件下,链接的分布不再是幂律分布而是更接近于正态分布。基于这些观测,作者提出了一个具有最低链接获得概率的择优依附生成模型。
另一个生成模型是Kumar等人研究的复制模型[23](2000),其中新节点会随机选择一个既存的节点并且复制它的部分链接。这样也会生成幂律分布。
有趣的是,网络的生长(添加新的节点)并不是产生无标度网络的必要条件。Dangalchev[24](2004)给出了生成静态无标度网络的示例。Caldarelli(2002)等人提出,另一种可能方案是将结构作为静态,然后根据两个顶点间的某个特定性质建立连接。一旦对这些顶点确定了概率分布(适应度 fitnesses),在一些情景下静态网络也可以发展出无标度网络的特性。
广义无标度模型
对无标度网络的模拟曾爆发式地出现。Barabási和Albert[25]的成果之后出现了许多的变体[26] [27] [28] [29] [22] ,几代的研究者,还有对过往数学成果的翻新。[30]只要模型中有幂律分布,那就是无标度网络,这个模型也即无标度模型。
特征
许多真实的网络都(近似)是无标度网络,因此需要无标度模型来描述它们。在普赖斯的体系里无标度模型需要两种组成部分:
1. 添加或者删除节点。通常我们更关注网络的生长,也就是添加节点。
2. 偏好依附。新节点会连接到“旧”节点的概率 [math]\displaystyle{ \Pi }[/math] 。
请注意适应度模型(见下方),在不改变节点个数的前提下,也可以静态地运作。还有一点需要注意的是,尽管“偏好依附”模型会生成无标度网络,然而这并不能证明这就是真实世界演化的机制,毕竟也许现实世界有其他同样可以产生规模效应的机制。
示例
以下是一些生成无标度网络特性的模型:
BA模型 The Barabási–Albert model
第一个无标度模型BA模型具有线性的偏好依附 [math]\displaystyle{ {\Pi} \left ( {k}_{i} \right )=\frac{{k}_{i}}{\sum _{j}{k}_{j}} }[/math] ,并且在每一步增加一个节点。
注意,现实网络中[math]\displaystyle{ \Pi \left ( k \right ) }[/math]的属性是[math]\displaystyle{ \Pi \left ( k \right )\neq 0 }[/math],新节点依附于一个孤立节点个概率不是零。因此 [math]\displaystyle{ {\Pi} \left ({k}\right ) }[/math] 的表达式为: [math]\displaystyle{ \Pi \left ( k \right )=A+k^{\alpha } }[/math] ,其中A是结点的初始吸引力。
双层网络模型 Two-level network model
Dangalchev[24]通过添加二级偏好依附规则构建了一个双层模型。一个节点的吸引力是一个双层模型,不仅与和它相连接的节点数量有关,也和和它二阶近邻的节点数量有关。 [math]\displaystyle{ {\Pi} \left ( k_{i} \right )=\frac{k_{i}+C\sum _{\left ( i,j \right )}k_{j}}{\sum _{j}k_{j}+C\sum _{j}k_{j}^{2}} }[/math],其中C是介于0和1之间的系数。
中介驱动依附模型 MDA model - mediation-driven attachment model
在中介依附模型中,一个具有m条边的新节点会随机选择一个既存的被连接的节点,然后将它自己连接到该节点以及该节点的随机选择的邻居上。既存节点被选择成为连接对象的概率[math]\displaystyle{ {\Pi} \left ( {i} \right ) }[/math]是 [math]\displaystyle{ {\Pi} \left ( {i} \right ) =\frac{k_{i}}{N}\frac{\sum _{k_{i}}^{j=1}\frac{1}{k_{j}}}{k_{i}} }[/math], 其中因子 [math]\displaystyle{ \frac{{\sum} _{{k}_{i}}^{j=1}\frac{1}{{k}_{j}}}{{k}_{i}} }[/math] 是节点 [math]\displaystyle{ i }[/math] 的 [math]\displaystyle{ k_{i} }[/math] 个邻居的度的调和平均(IHM)的倒数。数值研究表明对于很大的 [math]\displaystyle{ N }[/math] 的 [math]\displaystyle{ {m}\gt 14 }[/math] 的调和平均数平均值会接近一个定值,也就是说 [math]\displaystyle{ {\Pi} \left ( {i} \right )\propto {k}_{i} }[/math]。
这暗示一个节点的链接数越高(度越高),它获得链接的概率也就越大,因为它们可以通过中介以多种方式被连接。这在直觉上体现了富者更富的的机制(或者说是BA模型中的偏好依附规则)。因此,中介依附网络看上去是遵从偏好依附规则的。[31]
然而 [math]\displaystyle{ {m}=1 }[/math] 时它表现为一个“赢家全赢”的机制,这时全部节点的99%都有数值为1的度,唯有一个节点是“超级富有”的。随着[math]\displaystyle{ m }[/math]值的增加“超级富有节点”和“贫穷节点”之间的差距会缩小,而当 [math]\displaystyle{ {m}\gt 14 }[/math] 时则发现会从“赢家全赢”转变到“富者更富”的机制。
非线性偏好依附 Non-linear preferential attachment
BA模型假设任意节点依附于节点i的概率 [math]\displaystyle{ {\Pi} \left ({k}\right ) }[/math] 与节点 [math]\displaystyle{ {i} }[/math] 的度 [math]\displaystyle{ k }[/math] 成正比。这个假设由两个假说构成,一是 [math]\displaystyle{ {\Pi} \left ({k}\right ) }[/math] 由 [math]\displaystyle{ k }[/math] 决定,这与随机图中 [math]\displaystyle{ {\Pi} \left ({k}\right )=p }[/math] 形成对比,二是 [math]\displaystyle{ {\Pi} \left ({k}\right ) }[/math] 是自变量为 [math]\displaystyle{ k }[/math] 的线性函数。[math]\displaystyle{ {\Pi} \left ({k}\right ) }[/math]的精确形式不一定是线性的,并且当前研究表明度分布很大程度上由 [math]\displaystyle{ {\Pi} \left ({k}\right ) }[/math] 决定。
Krapivsky、Redner和Leyvraz[28]指出网络的无标度属性会被非线性的偏好依附破坏。唯一能让网络的拓扑结构具有无标度属性的情形是一个无限贴近线性 asymptotically linear的偏好依附,例如在 [math]\displaystyle{ {k}_{i}{\rightarrow} {\infty} }[/math] 时[math]\displaystyle{ \Pi \left ({k}_{i} \right )\sim \alpha _{\infty }{k}_{i} }[/math]。此时从这个比率等式可以得出 [math]\displaystyle{ \gamma =1+\frac{\mu}{\alpha _{\infty}} }[/math], 这样一来度分布的指数便可以取任何介于2和[math]\displaystyle{ {\infty} }[/math]之间的值。
层级网络模型 Hierarchical network model
还有一种无标度网络,它的生长是遵循某种模式,比如层级网络模型。[32]
迭代式架构形成了一种层级网络。从完全连接的五个节点开始,构建与此四个一模一样的复制,将他们每一簇的外围节点与初始的那簇的中心节点相连接。由此我们便获得了一个25 个节点的网络([math]\displaystyle{ N=25 }[/math])。重复相同的步骤,我们可以创建四个与初始那簇相同的四个复制,每个复制的四个外围节点再连接到第一个步骤中产生的四个簇的中心节点上。这样就获得了 [math]\displaystyle{ N=125 }[/math] 的网络,并且步骤可以无限继续。
适应度模型 Fitness model
适应度模型不随机地以等概率 [math]\displaystyle{ p }[/math] 给两个顶点分配链接,而是为每一个顶点 [math]\displaystyle{ {j} }[/math] 设有一个内含的适合性 [math]\displaystyle{ x_{j} }[/math] ,让顶点 [math]\displaystyle{ {j} }[/math] 和顶点 [math]\displaystyle{ i }[/math] 之间的链接以概率[math]\displaystyle{ p\left ( x_{i},x_{j} \right ) }[/math]产生。[33]在世界贸易网络中可以通过基于GDP的适应性来重建其中的网络特性,即: [math]\displaystyle{ {p}\left ( {x}_{i},{x}_{j} \right )=\frac{\delta {x}_{i},{x}_{j} }{1+{\delta} {x}_{i},{x}_{j}}. }[/math][34]
双曲几何图 Hyperbolic geometric graphs
假设一个网络内含复杂网络双曲几何模型形状,那么可以用空间网络生成无标度的度分布。这种混杂式的度分布体现了所含双曲几何形状双曲空间模型的负曲率和度量特性。[35]
边缘变换以生成具有所需属性的无标度图 Edge dual transformation to generate scale free graphs with desired properties
可以在低度相关性和聚类系数的无标度网络的基础上,通过应用边缘双变换来生成度相关性和聚类系数更高的新图。[14]
均匀偏好依附模型 Uniform-Preferential-Attachment model(UPA)
UPA模型是偏好依附模型的一个变种(由Pachon等人提出),它运用了两种不同的依附规则:一个是体现富者更富的偏好依附机制(概率是 [math]\displaystyle{ 1-p }[/math] ),还有一个是对最新的一些节点做均匀选择(概率是 [math]\displaystyle{ p }[/math] )。这个改动对于研究度分布的无标度表现的鲁棒性有一些妙用。分析证明它依旧保留了近似幂律的度分布。[22]
无标度理想网络
在网络理论中一个无标度理想网络是一个具有无标度理想气体密度分布 scale-free ideal gas density distribution的度分布的随机网络。当竞争性集群增长过程被应用于网络时,这些网络可以通过运用复杂网络的信息理论解译社交团体的规模分布来重现城市规模的分布和选举结果。[36][37]在无标度理想网络模型中,可以展示六度分离 six degrees of separation现象的成因正是邓巴数。
新特性
对于一个具有n个节点和幂律指数[math]\displaystyle{ \beta \gt 3 }[/math]的无标度网络,其感应子图 induced subgraph由度大于[math]\displaystyle{ log\left ( n \right )\times log^{\ast }\left ( n \right ) }[/math]的节点构成,是一个幂律指数[math]\displaystyle{ \beta'=2 }[/math]的无标度网络。[38]
Scale-Free Networks 原文翻译
——摘自《科学美国人》中文版2003.7
网络有随机网络和无尺度网络,许多网络包括因特网"人类社会和人体细胞代谢网络等,都是无尺度网络。研究无尺度网络,对于防备黑客攻击、防治流行病和开发新药等,都具有重要的意义。
(原文:Scale-Free Networks, pp50-59, May2003) 撰文/Albert-Laszlo Barabasi, Eeic Bonabeau)
本部分内容是由集智俱乐部成员翻译自巴拉巴西发表在《科学美国人》的Scale-Free Networks一文,主要由何毓嵩翻译,曾少立审校。
作者介绍
Albert-Laszlo Barabasi和Eric Bonabeau研究了从因特网到昆虫群落等一系列复杂系统的行为和特性。Barabasi是美国圣母大学的霍夫曼物理学教授。并在校内指导对复杂网络的研究,他著有《连结:网络新科学》一书。Bonabeau为美国麻省剑桥咨询公司"伊可系统"的首席科学家,专门运用复杂科学方面的工具来开发商业机会。他与别人合作撰写了《虫群智慧:从自然系统到人工系统》一书。这是他在本刊上第二次发表文章。
| 一个实例: 如图所示,因特网是一个无尺度网络,其中某些站点似乎与无数的其他站点相连结 (参见右图的星爆形结构细节)。本图绘制于2003年2月6日,描绘了从某一测试站点到其他约10万个站点的最短连结路径。图中以相同的颜色来表示相类似的站点。 |
大脑,是由轴突相连结的神经细胞网络,而细胞本身,又是由生化反应相连结的分子网络。社会也是一个网络,它由友情、家庭和职业关系彼此连结。在更大的尺度上,食物链和生态系统可以看作由物种所构成的网络。科技领域的网络更是随处可见:因特网、电力网和运输系统都是实例。就连在文章中我们用以向你传递思想的语言,也是一种藉由语法相互串连在一起的文字网络。
尽管网络是如此重要和普遍,但科学家对它的结构和属性却知之不多。在复杂的基因网络中,故障节点是如何相互作用而引发癌症的?在特定的社会和通信系统中,疾病和电脑病毒如何快速传播而导致流行?某些网络即便大部分节点失效,还能维持运行,原因何在?
最近的研究开始找到这些问题的答案。过去的几年中,不同领域的研究者发现,很多网络都是由少数一些具有众多连结的节点所支配的,包括万维网、细胞代谢系统,以及好莱坞的演员网络在内。包含这种重要节点(或称集散节点)的网络,我们通常称之为"无尺度"(scale free)网络。在无尺度网络中,有些集散节点甚至具有数不清的连结,而且不存在代表性的节点。这种网络还具有可预期的行为特性:例如对意外故障具有惊人的承受力,但面对协同式攻击时则很脆弱。
这些发现极大地改变了我们对复杂外部世界的认识。集散节点的存在,让我们认识到了以前的网络理论尚未涉及的问题:各种复杂系统具有相同的严格结构,都受制于某些基本的法则,这些法则似乎可同等地适用于细胞、计算机、语言和社会。更进一步,认识这些法则,会帮助我们解决一系列重要问题,包括开发更好的药物、防止黑客侵人互联网、阻止致命流行病的传播,等等。
| 概述 /无尺度网络的特性:
很多复杂系统拥有共同的重要特性:大部分节点只有少数几个连结,而某些节点却拥有与其他节点的大量连结。这些具有大量连结的节点称为“集散节点”,所拥有的连结可能高达数百、数千甚至数百万。由此看来,这一特性似乎能说明网络是无尺度的。 无尺度网络具有某些重要特性。例如它们都可以承受意外的故障,但面对协同式攻击却很脆弱。 了解这些特性,可能导致许多领域出现新的应用。例如,电脑科学家可能据此设计出更有效的策略,以保护因特网免受电脑病毒的侵害。 |
无尺度网络
在过去40多年里,科学家惯于将所有复杂网络看作是随机网络。这一思想源于两位匈牙利数学家的研究,他们是卓越的Erdos以及他的密切合作者Renyi。1959年,为了描述通信和生命科学中的网络,Erdos和Renyi提出,通过在网络节点间随机地布置连结,就可以有效地模拟出这类系统。这种方法及相关定理的简明扼要,导致了图论的复兴,数学界也因此出现了研究随机网络的新领域。
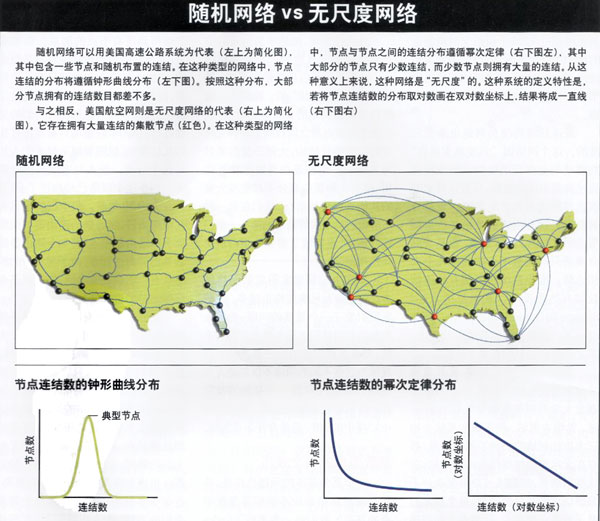
随机网络理论有一项重要预测:尽管连结是随机安置的,但由此形成的网络却是高度民主的,也就是说,绝大部分节点的连结数目会大致相同。实际上,随机网络中节点的分布方式将遵循钟形的泊松分布。连接数目比平均数高许多或低许多的节点,都十分罕见。有时随机网络也称作指数网络,因为一个节点连接k个其他节点的概率,会随着k值的增大而呈指数递减。
因此当1998年,我们与美国圣母大学的郑夏雄及Albert合作,开展一个描绘万维网的项目时,我们满以为会发现一个随机网络。原因如下:人们会根据自己的兴趣,来决定将网络文件连结到哪些网站,而个人兴趣是多种多样的,可选择的网页数量也极其庞大,因而最终的连结模式将呈现出相当随机的结果。
然而,实测结果却推翻了这个预测。在这个项目中,我们设计了一个软件,可从一个网页跳转到另一个,尽可能地收集网上的所有连结。虽然这个虚拟机器人仅仅探索了整个万维网的极小一部分,但它组合出来的图景。却揭示了令人惊异的事实:基本上,万维网是由少数高连结性的页面串连起来的,80%以上页面的连结数不到4个。然而只占节点总数不到万分之一的极少数节点,却有1000个以上的连结(一项后续的网络调查显示,有一份文件已经被超过200万的其他网页所连结!)。
我们在计算恰好拥有k个连结的万维网页面的数目时,发现网页的连结分布遵循所谓的"幂次定律":任何节点与其他k个节点相连结的概率,与l/k成正比。对于流入的连结而言,n值接近于2,这也就是说,流入连接数只有某站点一半的站点,在网中的数量却有该站点的4倍之多。幂次定律和表征随机网络的钟形分布大相径庭。具体来说,幂次定律不像钟形曲线那样具有一个峰值,而是由连续递减的函数来描述。如果用双对数坐标系来描述幂次定律,得到的是一条直线[见下图随机网络vs无尺度网络]。与随机网络中连结的民主分布不同,幂次定律所描述的,是由少数集散节点(如Yahoo和Google)所主控的系统。
随机网络中绝对不可能出现集散节点。当我们开始描绘万维网时,原本预期节点会像人类的身高一样遵循钟形分布,但结果却发现有些节点不能如此解释。我们就像突然发现了很多身高百尺的巨人一样,大吃了一惊。因此,我们想出了"无尺度"这样的用语。
无尺度网络在哪里?
过去几年中,研究者在很多不同的系统中都发现了无尺度结构。我们研究万维网的目标是以超连结彼此串连的虚拟网页网络。相比之下,美国加州大学河滨分校的Faloutsos、加拿大多伦多大学的Faloutsos以及美国卡耐基梅隆大学的Faloutsos则是分析因特网的物理结构。这三位电脑科学家兄弟研究了以光纤或其他通信线路连接的路由器,他们发现,这个实体网络的拓扑结构也是无尺性的。
研究人员还发现,某些社会网络也是无尺度的。例如,美国波士顿大学和瑞典斯德哥尔摩大学的科学家的共同研究显示,瑞典民众的性关系网络也遵循幂次定律:尽管大部分人终其一生只有少数几个性伴侣,但有少数人(集散节点)的性伴侣多达数百人。德国基尔大学的Bornholdt领导的一项研究表明,电子邮件所连结的人际网络,也可能是无尺度的。渡士顿大学的Redner则证实,由科学论文之间引用关系所连结的网络,同样也遵循幂次定律。美国密歇根大学安娜堡分校的Newman研究了包括物理和计算机等一些学科内科学家之间的合作关系网络,他发现这些网络同样也是无尺度的,这也印证了我们针对数学家和神经科学家所做的研究。(有趣的是,在数学界,Erdos本人就是最大的集散节点之一,他写的论文超过1400篇,其中共同作者不下500人。)
无尺度网络同样也出现在商业领域。美国斯坦福大学的W·Powell、加州大学lrvine分校的R·White、亚利桑那大学的W·Koput以及密歇根大学的Smith,共同研究了美国生物技术产业联盟网络的形成。发现存在特定的集散节点:Gerlzyme、Chiron和Genentech等公司,与其他公司相比,拥有的合作关系数量就多得不成比例。意大利的研究者对这种类型的网络进行了更深入的研究。利用意大利锡耶纳大学的"制药工业数据库"所提供的数据(该数据库目前包括超过7200个组织之间所签定的约20100个研发协议),研究人员发现,Powell等人所发现的那些集散节点,实际上也属于某个无尺度网络。
就连好莱坞演员网络也是无尺度的。这个网络因"六度凯文贝肯"的游戏而变得众所皆知。游戏玩家通过共同出演的电影,尽量让特定的演员与凯文贝肯产生关联。定量分析显示,这个网络也是由某些集散节点所支配的。具体来说,就是大部分演员只与为数不多的其他几个人相连结,而少数演员所拥有的连结数却高达数千个,其申包括Rod Steiger和Donald Pleasence。顺便说一下,在演员连结数的排行榜上,凯文贝肯自己只排在第876位。
重新回到严肃的话题,无尺度网络也出现在生物学领城。我们与美国西北大学的细胞生物学家Oltvai一道,发现古菌域、细菌域和真核生物三大生物领域的43种不同生物里,都存在无尺度的细胞代谢网络结构。在这些网络里,细胞通过分解复杂分子来燃烧食物并释放能量。每个特定的分子就是一个节点,而节点之间的连结则是生化反应。我们发现,大部分的分子只参加一种或两种反应,但是有少数分子(集散节点)会参与大部分的反应,比如水和三磷酸腺苷。
我们还发现,细胞中蛋白质的交互网络也是无尺度的。在这种网络中,如果两种蛋白质能相互反应,就认为是彼此"连结"的。我们在研究酵母这种最简单的真核细胞时,在它的数千个蛋白质之间找到了一种无尺度的网络拓扑结构:大部分蛋白质只与其他一、两种蛋白质发生相互作用,但有几种蛋白质分子却能与大量的其他蛋白质相结合。我们在另一种与酵母迥然不同的简单细菌——幽门螺杆菌中,也发现了类似的蛋白质交互作用网络。
事实上,科学家研究的网络越多,发现的无尺度结构也越多。这些发现引发了一个重要的问题:为什么像细胞和因特网这样本质上不同的系统,却具有相同的结构并遵从相同的规律?这些不同的网络不仅都是无尺度的,而且还有着一个有趣的共同点:由于某些未知的原因,幂次定律中kn项中的n值,通常介于2-3之间。
| 无尺度网络的例子: |
集散节点的马太效应
一个更为基本的问题也许是,为什么随机网络理论不能解释集散节点的存在?我们进一步考察了Erdos和Renyi的研究,发现这里面存在两个原因。
在建立模型的时候,Erdos和Renyi曾假设,他们在安置连结之前能够得到所有节点的清单。而事实上,万维网的页面数量绝对不是恒定的。1990年整个万维网只有一个网页,而到今天它的网页数已经超过了30亿。大部分网络也都具有类似的发展过程。1890年好莱坞只有屈指可数的几位演员,但随着越来越多的人加入这个行业,新人与之演员建立联系,如今这个网络已经超过了50万人。大约30年前,整个因特网只有几个路由器,随着新的路由器与网络原有的路由器相连结,如今路由器的数量已经高达百万。由于现实中的网络具有不断成长的本性,所以老节点获得连结的机会就比较高。
此外,并非所有的节点都是平等的。在选择将网页连结到何处时,人们可以从数十亿个网站中进行选择。然而我们大部分人只熟悉整个万维网的一小部分,这一小部分中往往包含那些拥有较多连结的站点,因为这样的站点更容易为人所知。只要连结到这些站点,就等于造就或加强了对它们的偏好。这种"优先连结"的过程,也发生在其他网络。在好莱坞,连结关系较多的影星更容易受到新秀们的重视。而在因特网上,那些连结较多的路由器通常还拥有更大的带宽,因而新用户就更倾向于连结到这些路由器上。在美国的生物技术产业内,象Genzyme这样的知名公司更容易吸引到同盟者,而这又进一步加强了它在未来合作中的吸引力。类似地,被引用较多的科学文献,会吸引更多的研究者去阅读和引用。美国著名的社会学家K·Merton将这种现象称之为"马太效应"。这个词来源于《新约》圣经的内容:"凡有的,还要加给他,叫他有余。"
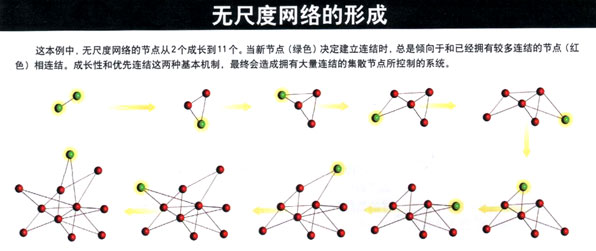
成长性和优先连结这两种机制,有助于解释集散节点的存在:当新节点出现时,它们更倾向于连结到已经有较多连结的节点,随着时间的推进,这些节点就拥有比其他节点更多 的连结数目。这种“富者逾富”的过程,有利于早期节点,它们更有可能成为集散节点。
我与阿Albert一道,进行了计算机模拟和计算,结果显示,具有优先连接的特性并且持续成长的网络,确实会发展成无尺度网络,并且节点的分布也遵循幂次定律,虽然这个理论模型过于简化,且需要根据具体情况加以调整,但还是对现实世界中无尺度网络的普遍存在提供了解释。
成长性和优先连接还能够解释生物系统中为什么会出现无尺度网络。例如,美国墨西哥大学的Wagner和英国牛津布鲁克斯大学的A·Fell就发现,大肠杆菌代谢网络中连结性较高的几种分子,一般具有更为久远的进化史:有些甚至被认为是所谓的RNA世界(DNA出现之前的进化阶段)的遗物,还有的则是最古老的代谢路径的一部分,
令人感兴趣的是,优先连结的机制常常是线性的。换句话说,如果一个现存节点的连结数是其相邻节点连结数的两倍,那么新节点与它连结的可能性,也是与邻近节点连结可能性的两倍。美国波士顿大学的Render及同事研究了不同类型的优先连结,他们发现。如果这种机制运行得比线性更快(例如,一个节点的连结数是另一个的两倍,而新节点连接到前者的可能性却是后者的4倍),那就容易出现一个攫取最多连结的集散节点,在这种"赢者通吃"的情况下,网络最终演变为拥有一个中心集散节点的星型拓扑结构。
无尺度网络的 "软肋"
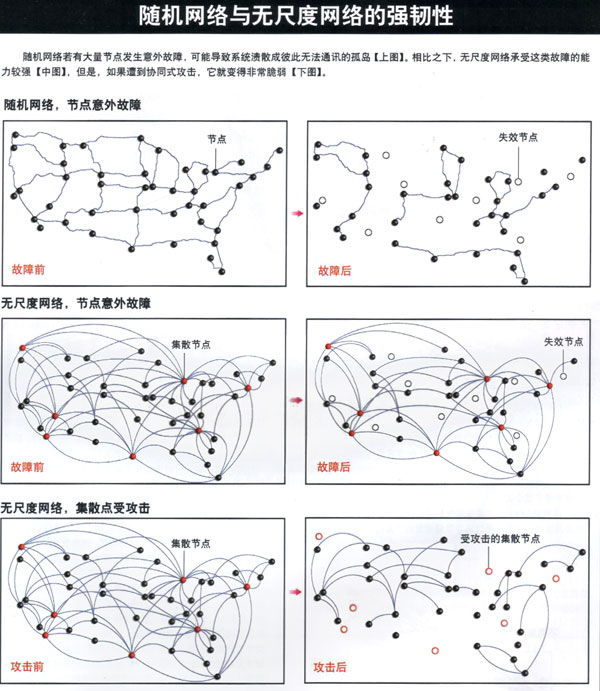
人们对电力网络和通信网络的依赖程度日益增高,凸现了一个广受关注的问题:这些网络到底有多可靠?好消息是复杂网络对意外故障具有很强的承受能力。实际上虽然每时每刻网络上都有数百个路由器失效,但因特网却很少因此受到大的影响。生命系统同样也具有这种强韧性:虽然细抱内存在诸如突变和蛋白质出错等数以千计的错误,但人体却极少因此发生严重的后果,这种强韧性的来源是什么呢?
直觉告诉我们,如果大部分节点发生瘫痪,将不可避免地导致网络的分裂。对随机网络而言,这是绝对正确的:随机网络中若有较大部分的节点被去除。网络必然溃散成彼此无法通讯的小型孤岛:不过无尺度网络的模拟结果,则展现了全然不同的情况:即使从因特网路由器中随机选择的失效节点比例高达80%,剩余的路由器还是能组成一个完整的集群并保证任意两个节点间存在通路。要扰乱细抱内的蛋白质交互网络也同样困难:我们的测量显示,即使在细胞内随机制造较高比例的突变,那些没有改变的蛋白质还是会正常地继续合作。
总的来说,无尺度网络对意外故障具有惊人的强韧性,这一特性本质上源于这些网络的非同质拓扑结构。随机去除的方式所破坏的主要是那些不重要的节点,因为它们的数目远大于集散节点。与那些几乎连结所有节点的集散节点相此。那些不重要的节点只拥有少量的连结。因而去除它们不会对网络拓扑结构产生重大的影响。但是,对集散节点的依赖,也带来了一个严重问题:面对蓄意攻击时,网络可能不堪一击。通过一系列的模拟,我们发现,只要去除少数几个主要集散节点,就可导致因特网溃散成孤立无援的小群路由器。类似地,对酵母的实验也显示,去除那些高连结性的蛋白质,比去除其他节点更容易导致酵母菌死亡。这些集散节点是决定性的,一旦发生使它们无法运作的突变,极有可能会导致整个细胞死亡。
对集散节点的依赖,视系统的不同,既有利也有弊。对因恃网和细胞而言,能够应付随机出现的意外故障,当然是个大优点。此外,细胞对集散节点的依赖,也给药物研究者提供了新的方法:有可能找到这样的药物,能针对性地攻击细胞或者细菌的集散节点,以便杀死它们而又不会影响健康的组织。不利的情况也有:少数消息灵通的黑客只要攻击一些集散节点,就足以搞垮整个通信基础网络,这正是人们关心的焦点。
无尺度网络的这一致命缺陷,引发了这样一个问题:到底有多少集散节点是必不可少的?最近的研究表明,总的来说,只要有5-10%的集散节点同时失效,就足以搞垮系统。我们对因特网的实验显示,一次有组织的协同攻击,只要去除掉若干个集散节点(先去除最大的,再去除次大的,依次类推),就足以造成重大破坏。因此,为了避免因恶意攻击带来网络的大规模破坏,最有效的办法就是保护好集散节点。不过,要想知道特定的网络系统到底有多容易被破坏掉,还有待进一步的研究。例如,如果Genzyme和Genentech这样的集散节点一起失去作用,是不是美国的生物产业会因此而崩溃呢?
"无尺度"流行病
对无尺度网络的认识,也可用于理解电脑病毒、疾病和时尚的传播。过去数十年间,无论是流行病学家还是市场营销专家,都在大力研究扩散理论。研究结果指出,一种传染病要在人群中传播开来,必须要跨越某一临界值。任何病毒、疾病或时尚的感染力一旦低于这个临界值,将不可避免地自行消亡;而一旦超过临界值,就会呈指数增长,最终传遍整个系统。
然而,西班牙巴塞罗那加泰罗尼亚理工大学的Pastor-satorras和意大利特里雅斯特国际理论物理研究中心的Vespigniani,最近却得出了一个令人不安的结论。他们发现,在无尺度网络里,不存在上面所说的临界值。这就意味着,所有病毒都可在网络中传播和长期存在,即便是那些传染力很低的病毒也是如此。这一结论解释了"爱虫"现象,(爱虫是有史以来最具破坏力的电脑病毒,2000年导致了英国议会电子邮件系统的瘫痪),这个病毒原本理当绝迹的,但过了一年之后,却仍然是最普遍的病毒之一。
因为集散节点会连结到很多其他节点、所以任何一个遭受病毒入侵的节点,都将连带感染至少一个集散节点。而一旦有集散节点被感染,它就会把病毒传播给众多的其他节点,当中也包括其他的集散节点,这就导致了病毒在整个网络里的传播。
社会网络在许多情况下也是无尺度的。生物病毒在社会网络里传播的现象,提醒科学家要再好好研究一下那些探讨网络拓扑结构和流行病之间互动关系的文献。特别是对于无尺度网络而言,公共卫生中传统的随机接种疫苗的方式可能很容易失效,因为它极有可能遗漏了某些集散节点。事实上,为了保证集散节点不被遗漏,几乎人人都得接种疫苗。例如,90%的人口都必须接种麻疹疫苗,才能够有效防疫。
如果医生放弃随机接种疫苗的方法,而把目标转向集散节点,也即那些最易感染的个人,情况会如何呢?对无尺度网络的研究指出,只要其中包含集散节点,即使接种疫苗的人口只占一小部分,这种方法仍有可能会奏效。
然而,要找出社会网络中的集散节点,比其他系统要难得多。尽管如此,以色列巴伊兰大学的Cohen和HavIin,以及美国克拉克森大学的ben-Avraham已提出了一个聪明的解决办法:任意选择一群人,请他们随机指定一位相识者,然后对这一小部分被指定的人接种疫苗。这一程序很可能会把集散节点圈入其中,理由是,集散节点与许多人都有连结,而连结性高的人更容易被指定。不过这一方法也存在一些道德上的困境。例如,即使识别出了集散节点,是否他们就有优先接种疫苗和接受治疗的权力呢?尽管存在这些问题,但对于那些无力照顾到全民的国家和地区而言,在分配艾滋病或天花疫苗时,这可能是最实用的办法。
出于各种商业目的,有时人们需要引发流行而不是遏制流行。例如所谓的病毒式行销,通常试图把集散节点当做行销的目标,以加快产品为用户所接受的速度。显然,这种策略已不是什么新鲜事了。早在1950年代,一项由制药业巨头辉瑞公司出资进行的研究发现,医生圈子中开始采用新药的速度,与集散节点有很大的关系。实际上,市场推广人员早就凭直觉知道,某些特定的消费者在促进新产品或新时尚方面,就是比其他的消费者管用得多。新近的无尺度网络研究,只是为更严谨地探讨这些现象,提供了一个科学的框架和数学工具。
从理论到应用之路
虽然无尺度网络很普遍,但仍有许多明显的例外。例如,美国的高速公路系统和电力网络就不是无尺度网络。材料科学中的大部分网络也不是。以晶格为例,各原子部和同样数目的邻近原子相连结。对于其他的一些网络,我们还难以得出定论。如反映捕食者与猎物关系的食物链网络,由于网络规模太小,科学家还难以断定它的型态。此外,由于缺乏大规模的人脑内部连结图,科学家也无法得知这一重要网络的本质。
确定某一网络是否无尺度,对了解该网络的行为特性是相当重要的,但是其他的重要指标也值得注意。其中参数之一就是网络的直径,或称为 "路径长度"。它指的是从一节点到另外的任意节点所需经过的最大的中间段数 [见下框文]。
虽然Milgram的结果很难说是定论,因为绝大部分的信件并未到达最终收信人手里·不过科学家最近发现,其他网络也具有这种 "小世界"的特性。例如,我们发现,细胞内的任意两种化学物质,几乎都能通过三个化学反应组成的路径连结起来。在万维网上,虽然页面数高达30亿,但一般只要经过19个连结,就可以从一个网页到达另一个。
从表面上看,由高度相互连结的节点在同类型的系统中,都存在相当明显的集群现象,其中包括美国电力网和线虫的神经网络等。 从表面上看,由高度相互连结的节点组成的孤立集群,似乎与无尺度网络的拓扑结构不相容·因为在无尺度网络中,有一些集散节点会与所有的节点相连结,它们的影晌是遍及整个系统的。但是最近我们发现,这两者其实是相容的:如果紧密连结的小型节点集群彼此相连,形成较大且较不紧密的大集团,那这样的网络就能既是高度集群的又是无尺度的 。这类结构在很多系统中都有出现·比如万维网,它的集群就是具有相同主题的网页群。细胞也是如此,它的集群就是负责特定功能的分子群。 |
最后,具备网络一般拓扑结构的知识,只能了解系统行为与全面特性的一部分。例如,在美国高速公路网这样的系统中,为其一指定节点添加一条连结的成本是极其昂贵的,这就阻止了它向无尺度方向发展。在食物链中,某些猎物比其他猎物更容易被猎取,这对整个生态系统具有深刻的影响。在社会网络中,家庭成员之间的关系比点头之交者要密切得多,因而疾病 (和信息)就更容易在这种连结中散播。对于运输、传送和通信系统 (如因恃网)而言,主要的问题是某些特定连结的拥堵:其一特定连结的流量过大,将导致该连结中断,而其他连结接手处理过剩流量,也可能会跟着失效。而且节点本身可能不具有同质性,如某些网页可能很有吸引力,那它就会严重影响优先连结的机制。
由于上述的种种原因,科学家可以说才刚开始了解无尺度网络的行为。例如,仅仅对集散节点免疫,也许并不足以阻止疾病的蔓延;更好的办法是,不仅仅考虑某人的连结数目,还要考虑这些连结的频度和接触时间。
基本上,我们在开始研究复杂网络时,会先忽略个别连结和节点的细节。通过远离这些细节,我们才能找出这些看似无法理解的系统背后的组织原则。我们的一些研究成果,至少已让研究者重新审视许多基本的假设。例如,研究者过去都把因特网视作随机网络,用来测试新的路由协议对系统塞车现象的影响。现在我们知道,因特网其实是一个无尺度网络,它的行为特性与随机网络有天壤之别。因此,像W·Byers和他在波士顿大学的同事们这样的研究者,正在修改因特网的电脑模拟模型。了解无尺度网络的特性,对其他许多领域都是有价值的,特别是当我们超越网络拓扑结构,进一步探讨复杂系统内部深奥得难以理解的动力学的时候。
| 无尺度网络的潜在意义:
运算 ·具有无尺度结构的计算机网络,例如万维网,对意外故障具有极强的承受能力,但面对蓄意的攻击和破坏却可能不堪一击。 ·要想在因特网上彻底清除病毒,即使是已知的病毒,也是不可能的。 医学 ·对天花等严重疾病的疫苗接种,如果能针对集散节点(即那些与很多人具有连结关系的人)进行,也许可以达到最大的效果,但要找出属于集散节点的人非常困难。 ·弄清人体细胞内的网络结构,将有助于研究者发现和控制药物的副作用。此外,若能识别出那些与特定疾病有关的集散点分子,就可开发只针对这些集散节点作用的新药物。 商业 ·了解公司、产业与经济之间的连结方式,有助于研究人员监控和预防大规模的经济衰退。 ·研究流行病在无尺度网络中的传播现象,为市场人员传播他们的新产品提供了新方法。 |
相关内容
参考文献
- ↑ Onnela, J. -P., Saramaki, J., Hyvonen, J., Lazer, G., Kaski, D., Kertesz, K., Barabasi, J., A. -L. (2007) "Structure and tie strengths in mobile communication networks".Proceedings of the National Academy of Sciences, doi:10.1073/pnas.0610245104. PMC 1863470. PMID 17456605..104.18:(7332--7336)
- ↑ Krzysztof Choromański,Michał Matuszak,Jacek Miȩkisz (2013) Scale-Free Graph with Preferential Attachment and Evolving Internal Vertex Structure.journal of statistical physics.151.6:(1175-1183)
- ↑ 3.0 3.1 Aaron Clauset, Cosma Rohilla Shalizi, M E J Newman () Power-Law Distributions in Empirical Data.51.4:(661-703)
- ↑ Broido (2019) "Scale-free networks are rare".Nature Communications.10.1:(1017)
- ↑ Barabási, Réka. (1999) "Emergence of scaling in random networks".Science.286.5439:(509--512)
- ↑ Bollobás, B., Riordan, O., Spencer, J., G. (2001) "The degree sequence of a scale-free random graph process".Random Structures and Algorithms.18.3:(279--290)
- ↑ Dorogovtsev, S. N., Mendes, J. F. F. (2002) "Evolution of networks".Advances in Physics.51,.(1079--1187)
- ↑ Willinger (2009) "Mathematics and the Internet: A Source of Enormous Confusion and Great Potential" (PDF). Notices of the AMS.American Mathematical Society.56.5:(586--599)
- ↑ Cohen, K., Avraham, D., Havlin, S. (2000) "Resilience of the Internet to Random Breakdowns".Physical Review Letters.85.21:(4626--4628)
- ↑ Cohen, K., Avraham, D., Havlin, S. (2001) ben-, "Breakdown of the Internet under Intentional Attack".Physical Review Letters.86.16:(3682--3685)
- ↑ Callaway, M. E. J., Watts, S. H., D. J. (2000) "Network Robustness and Fragility: Percolation on Random Graphs".Physical Review Letters.85.25:(5468--5471)
- ↑ Cohen, K., Avraham, D., Havlin, S. (2000) "Resilience of the Internet to Random Breakdowns".Physical Review Letters.85.21:(4626--4628)
- ↑ Cohen, Shlomo (2003) "Scale-Free Networks Are Ultrasmall".Physical Review Letters.90.5:
- ↑ 14.0 14.1 Ramezanpour, A., Karimipour, V., Mashaghi, A. (2003) "Generating correlated networks from uncorrelated ones".Phys.67.4:
- ↑ De Masi (2006) "Fitness model for the Italian interbank money market".Physical.74.6:
- ↑ Soramäki (2007) "The topology of interbank payment flows".Physica A: Statistical Mechanics and Its Applications.379.1:(317--333)
- ↑ Steyvers, Tenenbaum (2005) "The Large-Scale Structure of Semantic Networks: Statistical Analyses and a Model of Semantic Growth".Cognitive Science.29, 10.1:(41--78)
- ↑ Fratini (2010) "Scale-free structural organization of oxygen interstitials in La2CuO4+y".Nature.466.7308:(841--844)
- ↑ Poccia, Aeppli (2012) "Optimum inhomogeneity of local lattice distortions in La2CuO4+y".PNAS.109.39:(15685--15690)
- ↑ Hassan, M. K., Hassan, M. Z., Pavel, N. I. (2010) "Scale-free network topology and multifractality in a weighted planar stochastic lattice".New Journal of Physics.12.9:
- ↑ Hassan, M. K., Hassan, M. Z., Pavel, N. I. (2010) "Scale-free coordination number disorder and multifractal size disorder in weighted planar stochastic lattice".J. Phys.: Conf. Ser.297.(01)
- ↑ 22.0 22.1 22.2 Pachon, Shuyi, D (2018) "Scale-free behavior of networks with the copresence of preferential and uniform attachment rules".Physica D: Nonlinear Phenomena.371.(1--12)
- ↑ Kumar, Prabhakar (2000) Stochastic Models for the Web Graph.Foundations of Computer Science.(57--65)
- ↑ 24.0 24.1 Ch, Dangalchev (2004) Generation models for scale-free networks.Physica A.
- ↑ A.-L. Barab, Albert, R. (1999) “Emergence of Scaling in Random Networks”.Science.286.(509--512)
- ↑ Albert, R., Barabási, A.L. (2000) Topology of Evolving Networks: Local Events and Universality.Phys..85.24:
- ↑ Mendes, Dorogovtsev S. N., J. F. F. (2002) Evolution of networks.Advances in Physics.51.(1079--1187)
- ↑ 28.0 28.1 P. L. Krapivsky, S. Redner, and F. Leyvraz (2000) Connectivity of Growing Random Networks.Phys. Rev. Lett..85.
- ↑ Bosiljka Tadić (2001) Dynamics of directed graphs: the world-wide Web.Physica A: Statistical Mechanics and its Applications.293.
- ↑ Herbert A. Simon (1955) On a Class of Skew Distribution Functions.Biometrika.42.(10--440)
- ↑ Hassan, M. K., Islam, Syed (2017) "Degree distribution, rank-size distribution, and leadership persistence in mediation-driven attachment networks".Physica A.469.(23--30)
- ↑ Ravasz, E., Barabási (2003) "Hierarchical organization in complex networks".Phys. Rev. E, cond-mat/0206130. Bibcode:2003PhRvE..67b6112R. doi:10.1103/physreve.67.026112. PMID 12636753..67.(026112)
- ↑ Caldarelli, G. (2002) "Scale-free networks from varying vertex intrinsic fitness".Phys. Rev. Lett.89.(258702, 2002PhRvL)
- ↑ Garlaschelli, D. (2004) "Fitness-Dependent Topological Properties of the World Trade Web".Phys. Rev. Lett.93.
- ↑ Krioukov, Marián (2010) "Hyperbolic geometry of complex networks".Physical.82.3:
- ↑ Hernando; D. Villuendas, A., Vesperinas; M. Abad, C., Plastino (2009) "Unravelling the size distribution of social groups with information theory on complex networks".Physical Journal B.
- ↑ Moreira; Demétrius R. Paula; Raimundo N. Costa Filho; José S. Andrade, André A., Jr. (2006) "Competitive cluster growth in complex networks".Physical.73.
- ↑ Hasan Heydari, S. Mahmoud Taheri, Kaveh Kavousi (2018) "Distributed Maximal Independent Set on Scale-Free Networks", 02513 [cs.Computer Science.
编者推荐
无标度网络的生成模型
该文采用由 Barabási 和 Albert 于 1999 年提出的增长网络网络模型(BA 模型),并使用matlab程序模拟了BA网络的演化过程。
推荐课程
图与网络:社交网络分析
社会网络、复杂网络都是复杂性科学研究的热门话题。该课程以「无标度网络」为例,讲解了社交网络及Barabasi-Albert模型,并教学Mathematica中关于网络的一系列工具。
稳健又脆弱的无标度网络
该课程将以无标度网络——复杂网络研究的典型代表为核心,了解复杂网络研究中的不同结构及其特点,现实中的无标度网络和其特点,以及无标度网络正反面效应。
从无标度网络研究历史看想法传播
该课程从发现、建模和分析等维度,梳理了无标度网络的研究历史,包括对于存在的争议的分析,最后给出对网络科学未来发展的一些看法。
重访经典:无标度网络
该课程主要介绍Barabasi有关无标度网络的开山大作。Barabasi这部大作主要介绍了网络中的幂律分布特性,首次创建了无标度网络这一重要概念,并研究了其背后的生成机制——偏好连接(preferential attachment)。
本中文词条由Entropie参与编译,刘晶审校,薄荷,|陶庐编辑,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。