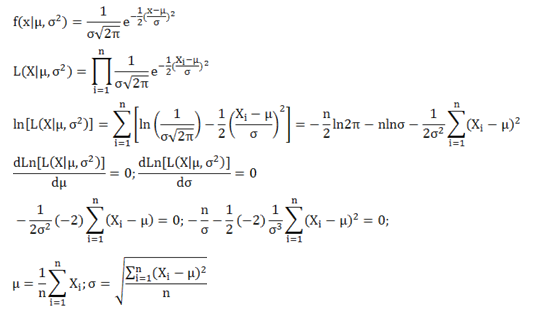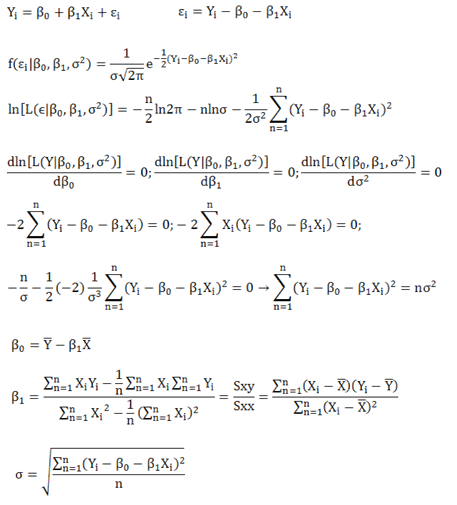最大似然参数估计
参数估计的一般方法
大部分参数估计方法,都是在取某种极值。例如最小二乘法要最小化误差的平方和
[math]\displaystyle{ S = \sum_{i=1}^{n} r_i^2 }[/math], [math]\displaystyle{ r_i = y_i - f(x_i, \beta) }[/math]
使用矩阵表达就是[math]\displaystyle{ f (x_i, \beta) = {x_i}^T \beta }[/math], 其中[math]\displaystyle{ \frac{\partial S}{\partial \beta_j} = 0 }[/math] 可以导出 [math]\displaystyle{ \hat \beta = (X^T X)^{-1}X^T y }[/math]
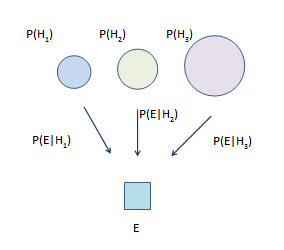
最大似然估计要最大化似然概率 (R. A. Fisher 1920)
[math]\displaystyle{ p(H_i|E) \sim p(E|H_i) }[/math]
贝叶斯估计要最大化贝叶斯概率 (T. Bayes, 1736)
[math]\displaystyle{ p(H_i|E) = \frac{p(E|H_i)p(H_i)}{\sum_j p(E|H_j)p(H_j)} }[/math]
实际上,最大似然估计可以看做是贝叶斯估计在先验分布为均匀分布情况下的特例。
以此类推,我们可以制造出各种新的估计方法,如最小化KS statistic等。
单变量分布参数估计:正态分布
假设有满足正态分布的一堆数据点{7.5,4.0,5.1,3.6,4.7,7.7,3.8,6.3,4.8,5.5},求参数。
推导正态分布的MLE estimator如下:
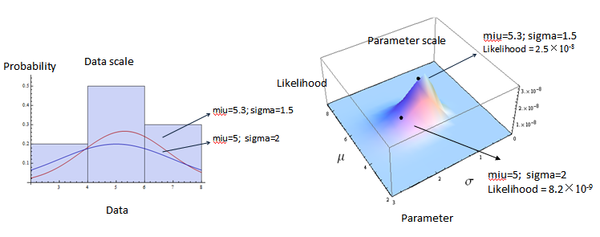
从以上结果中我们不仅可以得到参数的最大似然估计结果[math]\displaystyle{ \mu=5.3 }[/math],[math]\displaystyle{ \sigma=1.5 }[/math],还可以求得该估计结果对应的似然概率[math]\displaystyle{ 2.5 * 10^{-8} }[/math]。实际上,任意代入两个参数,我们都可以求出产生观察到的数据集的似然概率。
刚才的数据实际上是由[math]\displaystyle{ \mu=5 }[/math],[math]\displaystyle{ \sigma=2 }[/math]的理想正态分布生成。
这个案例让我们对参数空间的概念有了更深刻的认识:概率分布函数与观测所得数据之间只存在概率意义上的对应,而不是严格地一一对应的。这解释了为什么为什么我们需要寻找BLUE的estimator以及用P值等指标来做goodness-of-fit评价。
import numpy
import random
import scipy.stats as stats
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
from matplotlib.colors import BoundaryNorm
import numpy as np
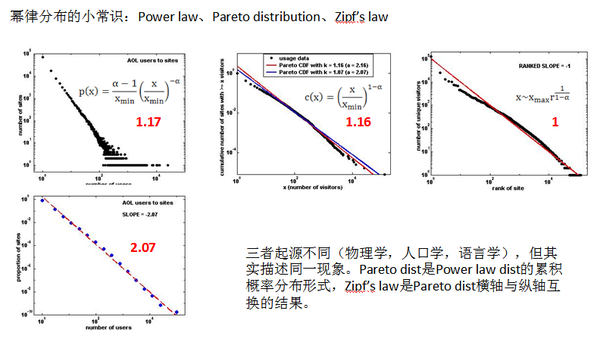
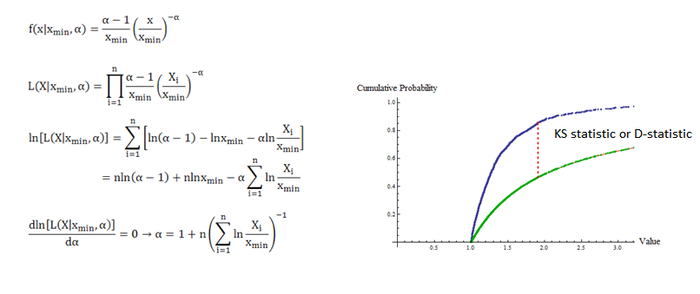
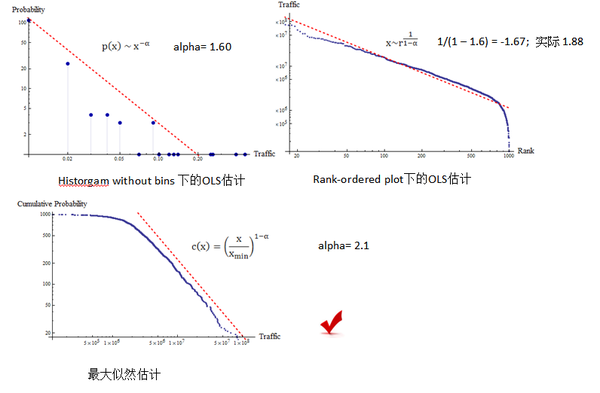
单变量分布参数估计:幂律分布
双变量线性回归参数估计
我们发现,在误差项为正态分布时,最大似然估计和最小二乘估计是等价的。但最大似然的思路非常清晰干净,而且可以直接推导出来,不需要记住Pearson相关等一大堆公式。
双变量logistic回归参数估计
请阅读这篇文章:
Maximum Likelihood Estimation of Logistic Regression Models: Theory and Implementation
并使用python实现对logistic回归的参数估计