条件互信息
在概率论中,特别是信息论中,条件互信息 Conditional mutual information [1][2]的基本形式表示为当给定第三个变量的情况下两个随机变量间互信息的期望值。
定义
对于具有支持集 Probability theory [math]\displaystyle{ \mathcal{X} }[/math], [math]\displaystyle{ \mathcal{Y} }[/math] 和 [math]\displaystyle{ \mathcal{Z} }[/math]的随机变量[math]\displaystyle{ X }[/math], [math]\displaystyle{ Y }[/math]和 [math]\displaystyle{ Z }[/math],我们将条件互信息定义为:
- [math]\displaystyle{ I(X;Y|Z) = \int_\mathcal{Z} D_{\mathrm{KL}}( P_{(X,Y)|Z} \| P_{X|Z} \otimes P_{Y|Z} ) dP_{Z} }[/math]
这可以用期望运算符来表示:
- [math]\displaystyle{ I(X;Y|Z) = \mathbb{E}_Z [D_{\mathrm{KL}}( P_{(X,Y)|Z} \| P_{X|Z} \otimes P_{Y|Z} )] }[/math].
因此,相较于互信息的定义,[math]\displaystyle{ I(X;Y|Z) }[/math]可以表达为期望的Kullback–Leibler散度(相对于[math]\displaystyle{ Z }[/math]),即从条件联合分布[math]\displaystyle{ P_{(X,Y)|Z} }[/math]到条件边际[math]\displaystyle{ P_{X|Z} }[/math] 和 [math]\displaystyle{ P_{Y|Z} }[/math]的乘积。
关于离散分布的概率质量函数
对于具有支持集[math]\displaystyle{ X }[/math], [math]\displaystyle{ Y }[/math], 和 [math]\displaystyle{ Z }[/math]的离散随机变量[math]\displaystyle{ \mathcal{X} }[/math], [math]\displaystyle{ \mathcal{Y} }[/math] 和 [math]\displaystyle{ \mathcal{Z} }[/math],条件互信息[math]\displaystyle{ I(X;Y|Z) }[/math]如下:
- [math]\displaystyle{ I(X;Y|Z) = \sum_{z\in \mathcal{Z}} p_Z(z) \sum_{y\in \mathcal{Y}} \sum_{x\in \mathcal{X}} p_{X,Y|Z}(x,y|z) \log \frac{p_{X,Y|Z}(x,y|z)}{p_{X|Z}(x|z)p_{Y|Z}(y|z)} }[/math]
其中边缘概率质量函数,联合概率质量函数,和(或)条件概率质量函数可以由[math]\displaystyle{ p }[/math]加上适当的下标表示。这可以简化为:
- [math]\displaystyle{ I(X;Y|Z) = \sum_{z\in \mathcal{Z}} \sum_{y\in \mathcal{Y}} \sum_{x\in \mathcal{X}} p_{X,Y,Z}(x,y,z) \log \frac{p_Z(z)p_{X,Y,Z}(x,y,z)}{p_{X,Z}(x,z)p_{Y,Z}(y,z)}. }[/math]
关于连续分布的概率密度函数
对于具有支持集[math]\displaystyle{ X }[/math], [math]\displaystyle{ Y }[/math], 和 [math]\displaystyle{ Z }[/math]的(绝对)连续随机变量[math]\displaystyle{ \mathcal{X} }[/math], [math]\displaystyle{ \mathcal{Y} }[/math] 和 [math]\displaystyle{ \mathcal{Z} }[/math],条件互信息[math]\displaystyle{ I(X;Y|Z) }[/math]如下:
- [math]\displaystyle{ I(X;Y|Z) = \int_{\mathcal{Z}} \bigg( \int_{\mathcal{Y}} \int_{\mathcal{X}} \log \left(\frac{p_{X,Y|Z}(x,y|z)}{p_{X|Z}(x|z)p_{Y|Z}(y|z)}\right) p_{X,Y|Z}(x,y|z) dx dy \bigg) p_Z(z) dz }[/math]
其中边缘概率密度函数,联合概率密度函数,和(或)条件概率密度函数 可以由p加上适当的下标表示。这可以简化为
- [math]\displaystyle{ I(X;Y|Z) = \int_{\mathcal{Z}} \int_{\mathcal{Y}} \int_{\mathcal{X}} \log \left(\frac{p_Z(z)p_{X,Y,Z}(x,y,z)}{p_{X,Z}(x,z)p_{Y,Z}(y,z)}\right) p_{X,Y,Z}(x,y,z) dx dy dz. }[/math]
部分特性
同时我们也可以将联合和条件熵写为[3]:
- [math]\displaystyle{ I(X;Y|Z) = H(X,Z) + H(Y,Z) - H(X,Y,Z) - H(Z) = H(X|Z) - H(X|Y,Z) = H(X|Z)+H(Y|Z)-H(X,Y|Z). }[/math]
这么表达以显示其与互信息的关系
- [math]\displaystyle{ I(X;Y|Z) = I(X;Y,Z) - I(X;Z) }[/math]
通常情况下,表达式被重新整理为“互信息的链式法则”
- [math]\displaystyle{ I(X;Y,Z) = I(X;Z) + I(X;Y|Z) }[/math]
上述式子的另一种等价形式是[4]:
- [math]\displaystyle{ I(X;Y|Z) = H(Z|X) + H(X) + H(Z|Y) + H(Y) - H(Z|X,Y) - H(X,Y) - H(Z) = I(X;Y) + H(Z|X) + H(Z|Y) - H(Z|X,Y) - H(Z) }[/math]
类似互信息一样,条件互信息可以表示为KL散度:
- [math]\displaystyle{ I(X;Y|Z) = D_{\mathrm{KL}}[ p(X,Y,Z) \| p(X|Z)p(Y|Z)p(Z) ]. }[/math]
或作为更简单的KL散度的期望值:
- [math]\displaystyle{ I(X;Y|Z) = \sum_{z \in \mathcal{Z}} p( Z=z ) D_{\mathrm{KL}}[ p(X,Y|z) \| p(X|z)p(Y|z) ] }[/math],
- [math]\displaystyle{ I(X;Y|Z) = \sum_{y \in \mathcal{Y}} p( Y=y ) D_{\mathrm{KL}}[ p(X,Z|y) \| p(X|Z)p(Z|y) ] }[/math].
其他通用定义
条件互信息的其他通用定义(适用于具有连续或其他任意分布的随机变量)将取决于 正则条件概率 Regular conditional probability 的概念。(参阅[5][6]))
令[math]\displaystyle{ (\Omega, \mathcal F, \mathfrak P) }[/math]为一个 概率空间 Probability space ,并将随机变量[math]\displaystyle{ X }[/math], [math]\displaystyle{ Y }[/math]和 [math]\displaystyle{ Z }[/math]分别定义为一个从[math]\displaystyle{ \Omega }[/math]到具有拓扑结构的状态空间的 波莱尔可测函数 Borel-measurable function 。
考虑到在每个随机变量状态空间中的波莱尔测度 Borel measure(关于开放集生成的σ代数),是由[math]\displaystyle{ \mathcal F }[/math]中每个波莱尔集分配到的的原像[math]\displaystyle{ \mathfrak P }[/math]测度来确定的。这被称为 前推测度 Pushforward measure [math]\displaystyle{ X _* \mathfrak P = \mathfrak P\big(X^{-1}(\cdot)\big). }[/math]。随机变量的支撑集定义为该测度的拓扑支撑集,即[math]\displaystyle{ \mathrm{supp}\,X = \mathrm{supp}\,X _* \mathfrak P. }[/math]。
现在,我们可以在给定其中一个随机变量值(或通过 积拓扑 product topology 获得更多)的情况下正式定义条件概率测度 Conditional probability distribution 。令[math]\displaystyle{ M }[/math]为[math]\displaystyle{ \Omega }[/math]的可测子集(即[math]\displaystyle{ M \in \mathcal F, }[/math]),令[math]\displaystyle{ x \in \mathrm{supp}\,X }[/math]。然后,使用 分解定理 Disintegration theorem :
- [math]\displaystyle{ \mathfrak P(M | X=x) = \lim_{U \ni x} \frac {\mathfrak P(M \cap \{X \in U\})} {\mathfrak P(\{X \in U\})} \qquad \textrm{and} \qquad \mathfrak P(M|X) = \int_M d\mathfrak P\big(\omega|X=X(\omega)\big), }[/math]
在[math]\displaystyle{ x }[/math]的开放邻域[math]\displaystyle{ U }[/math]处取极限,因为相对于集包含 Set inclusion,它们可以任意变小。
最后,我们可以通过 勒贝格积分 Lebesgue integration来定义条件互信息:
- [math]\displaystyle{ I(X;Y|Z) = \int_\Omega \log \Bigl( \frac {d \mathfrak P(\omega|X,Z)\, d\mathfrak P(\omega|Y,Z)} {d \mathfrak P(\omega|Z)\, d\mathfrak P(\omega|X,Y,Z)} \Bigr) d \mathfrak P(\omega), }[/math]
其中被积函数是拉东-尼科迪姆导数 Radon–Nikodym derivative的对数,涉及我们刚刚定义的一些条件概率测度。
注释符号
在诸如[math]\displaystyle{ I(A;B|C) }[/math]的表达式中,[math]\displaystyle{ A }[/math] [math]\displaystyle{ B }[/math] 和 [math]\displaystyle{ C }[/math]不限于表示单个随机变量,它们同时可以表示在同一概率空间上定义的任意随机变量集合的联合分布。类似概率论中的表达方式,我们可以使用逗号来表示这种联合分布,例如[math]\displaystyle{ I(A_0,A_1;B_1,B_2,B_3|C_0,C_1) }[/math]。因此,使用分号(或有时用冒号或楔形[math]\displaystyle{ \wedge }[/math])来分隔互信息符号的主要参数。(在联合熵的符号中,不需要作这样的区分,因为任意数量随机变量的 联合熵 Joint entropy与它们联合分布的熵相同。)
属性
非负性
对于离散,联合分布的随机变量X,Y和Z,如下不等式永远成立:
- [math]\displaystyle{ I(X;Y|Z) \ge 0 }[/math],
该结果已被用作证明信息理论中其他不等式的基础,尤其是香农不等式。对于某些正则条件下的连续随机变量,条件互信息也是非负的[7]。
交互信息
考虑到第三个随机变量条件可能会增加或减少 互信息:例如其差值[math]\displaystyle{ I(X;Y) - I(X;Y|Z) }[/math],称为 交互信息 Interaction information (注意区分互信息Mutual information),可以为正,负或零。即使随机变量是成对独立的也是如此。比如以下情况下:
- [math]\displaystyle{ X \sim \mathrm{Bernoulli}(0.5), Z \sim \mathrm{Bernoulli}(0.5), \quad Y=\left\{\begin{array}{ll} X & \text{if }Z=0\\ 1-X & \text{if }Z=1 \end{array}\right. }[/math]
- [math]\displaystyle{ X }[/math], [math]\displaystyle{ Y }[/math] 和 [math]\displaystyle{ Z }[/math]是成对独立的,特别是[math]\displaystyle{ I(X;Y)=0 }[/math],不过这里[math]\displaystyle{ I(X;Y|Z)=1. }[/math]。
互信息的链式法则
- [math]\displaystyle{ I(X;Y,Z) = I(X;Z) + I(X;Y|Z) }[/math]
多元互信息
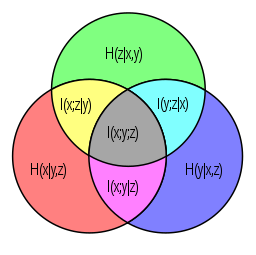
结合信息图中的集合或度量理论,可以用条件互信息来归纳定义多元互信息。其定义表达式如下:
- [math]\displaystyle{ I(X_1;\ldots;X_{n+1}) = I(X_1;\ldots;X_n) - I(X_1;\ldots;X_n|X_{n+1}), }[/math]
其中
- [math]\displaystyle{ I(X_1;\ldots;X_n|X_{n+1}) = \mathbb{E}_{X_{n+1}} [D_{\mathrm{KL}}( P_{(X_1,\ldots,X_n)|X_{n+1}} \| P_{X_1|X_{n+1}} \otimes\cdots\otimes P_{X_n|X_{n+1}} )]. }[/math]
该定义与交互信息的定义相同,只是在随机数为奇数的情况下符号发生了变化。一个复杂的问题是,该多元互信息(以及交互信息)可以是正,负或零,这使得其数量难以直观地解释。实际上,对于n个随机变量,存在2n-1个自由度。那么如何在信息理论上将它们关联,并对应于这些变量的每个非空子集,就是解决问题的关键。特别是这些自由度受到信息论中各种香农和非香农不等式的制约。
参考文献
- ↑ Wyner, A. D. (1978). "A definition of conditional mutual information for arbitrary ensembles". Information and Control. 38 (1): 51–59. doi:10.1016/s0019-9958(78)90026-8.
- ↑ Dobrushin, R. L. (1959). "General formulation of Shannon's main theorem in information theory". Uspekhi Mat. Nauk. 14: 3–104.
- ↑ Cover, Thomas; Thomas, Joy A. (2006). Elements of Information Theory (2nd ed.). New York: Wiley-Interscience. ISBN 0-471-24195-4.
- ↑ Decomposition on Math.StackExchange
- ↑ Regular Conditional Probability on PlanetMath
- ↑ D. Leao, Jr. et al. Regular conditional probability, disintegration of probability and Radon spaces. Proyecciones. Vol. 23, No. 1, pp. 15–29, May 2004, Universidad Católica del Norte, Antofagasta, Chile PDF
- ↑ Polyanskiy, Yury; Wu, Yihong (2017). Lecture notes on information theory. p. 30. http://people.lids.mit.edu/yp/homepage/data/itlectures_v5.pdf.
编者推荐
集智课程
信息论
信息论(information theory)涉及信息的量化、存储和通信等。信息论是由克劳德·香农发展来的,用来找出信号处理与通信操作的基本限制,如数据压缩、可靠的存储和数据传输等。自创立以来,它已拓展应用到许多其他领域,包括统计推断、密码学、神经生物学、进化论、量子计算、剽窃检测和其他形式的数据分析。
在本课程中,融合经典和现代信息论的成果,为信息科学方向学生提供一个统一的信息论基础,也可作为专业入门课程。主要讲解了熵,熵率,微分熵,AEP,数据压缩和信道的相关知识。
相关文章
本中文词条由Jie翻译,Flipped审校,薄荷编辑,如有问题,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。