极限环

此词条暂小竹凉翻译，翻译字数共657，未经人工整理和审校，带来阅读不便，请见谅。

Stable limit cycle (shown in bold) and two other trajectories spiraling into it 稳定的极限环(粗体显示)和另外两个螺旋进入它的轨迹

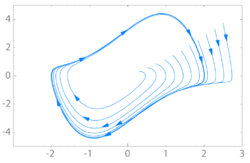
Stable limit cycle (shown in bold) and two other trajectories spiraling into it

稳定极限环以及另外两个轨迹以螺旋方式进入

Stable limit cycle (shown in bold) for the Van der Pol oscillator 范德波尔振荡器 Van der Pol oscillator的稳定极限环(粗体显示)

Stable limit cycle (shown in bold) for the Van der Pol oscillator

范德波尔振荡器 Van der Pol oscillator中的稳定极限环。

In mathematics, in the study of dynamical systems with two-dimensional phase space, a limit cycle is a closed trajectory in phase space having the property that at least one other trajectory spirals into it either as time approaches infinity or as time approaches negative infinity. Such behavior is exhibited in some nonlinear systems. Limit cycles have been used to model the behavior of a great many real-world oscillatory systems. The study of limit cycles was initiated by Henri Poincaré (1854–1912).

In mathematics, in the study of dynamical systems with two-dimensional phase space, a limit cycle is a closed trajectory in phase space having the property that at least one other trajectory spirals into it either as time approaches infinity or as time approaches negative infinity. Such behavior is exhibited in some nonlinear systems. Limit cycles have been used to model the behavior of a great many real-world oscillatory systems. The study of limit cycles was initiated by Henri Poincaré (1854–1912).

在数学 Mathematics上，二维相空间 Phase Space 动力系统 Dynamical Systems的研究中，极限环是一个在相空间中的闭合轨迹 Trajectory，它具有当时间趋于无穷大或时间趋于负无穷大时至少有一条其他轨迹螺旋进入的性质。这种行为在一些非线性系统 Nonlinear Systems中表现出来。极限环已经被用来模拟许多实际振动系统的行为。对极限环的研究是由亨利·庞加莱 'Henri poincaré(1854-1912)提出的。

Definition

定义

We consider a two-dimensional dynamical system of the form

We consider a two-dimensional dynamical system of the form

我们考虑一个二维动力系统的形式

[math]\displaystyle{ x'(t)=V(x(t)) }[/math]

[math]\displaystyle{ x'(t)=V(x(t)) }[/math]

where

where

当

[math]\displaystyle{ V:\mathbb{R}^2\to\mathbb{R}^2 }[/math]

[math]\displaystyle{ V:\mathbb{R}^2\to\mathbb{R}^2 }[/math]

is a smooth function. A trajectory of this system is some smooth function [math]\displaystyle{ x(t) }[/math] with values in [math]\displaystyle{ \mathbb{R}^2 }[/math] which satisfies this differential equation. Such a trajectory is called closed (or periodic) if it is not constant but returns to its starting point, i.e. if there exists some [math]\displaystyle{ t_0\gt 0 }[/math] such that [math]\displaystyle{ x(t+t_0)=x(t) }[/math] for all [math]\displaystyle{ t\in\mathbb{R} }[/math]. An orbit is the image of a trajectory, a subset of [math]\displaystyle{ \mathbb{R}^2 }[/math]. A closed orbit, or cycle, is the image of a closed trajectory. A limit cycle is a cycle which is the limit set of some other trajectory.

is a smooth function. A trajectory of this system is some smooth function [math]\displaystyle{ x(t) }[/math] with values in [math]\displaystyle{ \mathbb{R}^2 }[/math] which satisfies this differential equation. Such a trajectory is called closed (or periodic) if it is not constant but returns to its starting point, i.e. if there exists some [math]\displaystyle{ t_0\gt 0 }[/math] such that [math]\displaystyle{ x(t+t_0)=x(t) }[/math] for all [math]\displaystyle{ t\in\mathbb{R} }[/math]. An orbit is the image of a trajectory, a subset of [math]\displaystyle{ \mathbb{R}^2 }[/math]. A closed orbit, or cycle, is the image of a closed trajectory. A limit cycle is a cycle which is the limit set of some other trajectory.

是一个平滑函数。这个系统的轨迹是满足这个微分方程的光滑函数。如果这个轨迹不是恒定的，而是返回到它的起始点，那么这个轨迹称为闭合(或周期)轨迹。如果存在一些 [math]\displaystyle{ t_0\gt 0 }[/math]有[math]\displaystyle{ x(t+t_0)=x(t) }[/math]对于所有的[math]\displaystyle{ t\in\mathbb{R} }[/math]。轨道 orbit是轨迹的图像 image，是[math]\displaystyle{ \mathbb{R}^2 }[/math]的子集。一个闭合轨道，或循环，是一个闭合轨迹的图像。极限环是一个循环，它是其他轨迹的极限集。

Properties

属性

By the Jordan curve theorem, every closed trajectory divides the plane into two regions, the interior and the exterior of the curve.

By the Jordan curve theorem, every closed trajectory divides the plane into two regions, the interior and the exterior of the curve.

通过若尔当曲线定理 Jordan Curve Theorem，每一个封闭的轨迹将平面分成两个区域，内部和外部的曲线。

Given a limit cycle and a trajectory in its interior that approaches the limit cycle for time approaching [math]\displaystyle{ + \infty }[/math], then there is a neighborhood around the limit cycle such that all trajectories in the interior that start in the neighborhood approach the limit cycle for time approaching [math]\displaystyle{ + \infty }[/math]. The corresponding statement holds for a trajectory in the interior that approaches the limit cycle for time approaching [math]\displaystyle{ - \infty }[/math], and also for trajectories in the exterior approaching the limit cycle.

Given a limit cycle and a trajectory in its interior that approaches the limit cycle for time approaching [math]\displaystyle{ + \infty }[/math], then there is a neighborhood around the limit cycle such that all trajectories in the interior that start in the neighborhood approach the limit cycle for time approaching [math]\displaystyle{ + \infty }[/math]. The corresponding statement holds for a trajectory in the interior that approaches the limit cycle for time approaching [math]\displaystyle{ - \infty }[/math], and also for trajectories in the exterior approaching the limit cycle.

给定一个极限环和它内部在时间上趋近[math]\displaystyle{ + \infty }[/math]的接近极限环的轨迹，在极限环周围有一个邻域，这样所有内部开始的轨迹在时间上趋近[math]\displaystyle{ + \infty }[/math]时都接近极限环。相应的陈述适用于时间上趋近[math]\displaystyle{ - \infty }[/math]的接近极限环的内部轨道，也适用于接近极限环的外部轨道。

Stable, unstable and semi-stable limit cycles

稳定、不稳定和半稳定极限环

In the case where all the neighboring trajectories approach the limit cycle as time approaches infinity, it is called a stable or attractive limit cycle (ω-limit cycle). If instead, all neighboring trajectories approach it as time approaches negative infinity, then it is an unstable limit cycle (α-limit cycle). If there is a neighboring trajectory which spirals into the limit cycle as time approaches infinity, and another one which spirals into it as time approaches negative infinity, then it is a semi-stable limit cycle. There are also limit cycles that are neither stable, unstable nor semi-stable: for instance, a neighboring trajectory may approach the limit cycle from the outside, but the inside of the limit cycle is approached by a family of other cycles (which wouldn't be limit cycles).

In the case where all the neighboring trajectories approach the limit cycle as time approaches infinity, it is called a stable or attractive limit cycle (ω-limit cycle). If instead, all neighboring trajectories approach it as time approaches negative infinity, then it is an unstable limit cycle (α-limit cycle). If there is a neighboring trajectory which spirals into the limit cycle as time approaches infinity, and another one which spirals into it as time approaches negative infinity, then it is a semi-stable limit cycle. There are also limit cycles that are neither stable, unstable nor semi-stable: for instance, a neighboring trajectory may approach the limit cycle from the outside, but the inside of the limit cycle is approached by a family of other cycles (which wouldn't be limit cycles).

当所有相邻轨迹在时间趋于无穷大时都接近极限环时，称之为稳定 Stable或吸引极限环(ω- 极限环)。当时间趋近于负无穷时，若所有相邻轨线都逼近它，则它是一个不稳定的极限环(α- 极限环)。如果存在一个相邻轨迹，当时间趋于无穷大时螺旋进入极限环，另一个轨迹在时间趋于负无穷大时螺旋进入极限环，那么它是一个半稳定的极限环。还有一些既不稳定、不稳定也不半稳定的极限环: 例如，邻近轨迹可能从外部接近极限环，但极限环的内部是由一组其他的极限环逼近的(不会是极限环)。

Stable limit cycles are examples of attractors. They imply self-sustained oscillations: the closed trajectory describes the perfect periodic behavior of the system, and any small perturbation from this closed trajectory causes the system to return to it, making the system stick to the limit cycle.

Stable limit cycles are examples of attractors. They imply self-sustained oscillations: the closed trajectory describes the perfect periodic behavior of the system, and any small perturbation from this closed trajectory causes the system to return to it, making the system stick to the limit cycle.

稳定极限环是吸引子 Attractor的例子。它们意味着自我维持的振荡 Oscillation: 闭合轨迹描述了系统的完美周期行为，任何来自这个闭合轨迹的微小扰动都会导致系统返回到它，使系统保持极限环。

Finding limit cycles

寻找极限环

Every closed trajectory contains within its interior a stationary point of the system, i.e. a point [math]\displaystyle{ p }[/math] where [math]\displaystyle{ V(p)=0 }[/math]. The Bendixson–Dulac theorem and the Poincaré–Bendixson theorem predict the absence or existence, respectively, of limit cycles of two-dimensional nonlinear dynamical systems.

Every closed trajectory contains within its interior a stationary point of the system, i.e. a point [math]\displaystyle{ p }[/math] where [math]\displaystyle{ V(p)=0 }[/math]. The Bendixson–Dulac theorem and the Poincaré–Bendixson theorem predict the absence or existence, respectively, of limit cycles of two-dimensional nonlinear dynamical systems.

每一个闭合轨迹在其内部都包含一个系统的驻点 Stationary Point，即点[math]\displaystyle{ p }[/math]当有[math]\displaystyle{ V(p)=0 }[/math].本迪克森-杜拉克定理 Bendixson–Dulac theorem和庞加莱-本迪克森定理 Poincaré–Bendixson theorem 分别预言了二维非线性动力系统极限环的缺失或存在。

Open problems

未解决的问题

Finding limit cycles, in general, is a very difficult problem. The number of limit cycles of a polynomial differential equation in the plane is the main object of the second part of Hilbert's sixteenth problem. It is unknown, for instance, whether there is any system [math]\displaystyle{ x'=V(x) }[/math] in the plane where both components of [math]\displaystyle{ V }[/math] are quadratic polynomials of the two variables, such that the system has more than 4 limit cycles.

Finding limit cycles, in general, is a very difficult problem. The number of limit cycles of a polynomial differential equation in the plane is the main object of the second part of Hilbert's sixteenth problem. It is unknown, for instance, whether there is any system [math]\displaystyle{ x'=V(x) }[/math] in the plane where both components of [math]\displaystyle{ V }[/math] are quadratic polynomials of the two variables, such that the system has more than 4 limit cycles.

一般来说，寻找极限环是一个非常困难的问题。平面上一个多项式微分方程的极限环的个数是希尔伯特第十六题 Hilbert's sixteenth problem第二部分的主要对象。例如，在平面上是否存在一个系统[math]\displaystyle{ x'=V(x) }[/math]，其中[math]\displaystyle{ V }[/math]的两个组成部分都是两个变量的二次多项式，这样的系统有多于4个极限环。

Applications

应用

Examples of limit cycles branching from fixed points near Hopf bifurcation. Trajectories in red, stable structures in dark blue, unstable structures in light blue. The parameter choice determines the occurrence and stability of limit cycles.

Examples of limit cycles branching from fixed points near Hopf bifurcation. Trajectories in red, stable structures in dark blue, unstable structures in light blue. The parameter choice determines the occurrence and stability of limit cycles.

极限环从霍普夫分岔 Hopf bifurcation附近的不动点分支的例子。红色的轨迹，深蓝色的稳定结构，浅蓝色的不稳定结构。参数的选择决定了极限环的出现和稳定性

Limit cycles are important in many scientific applications where systems with self-sustained oscillations are modelled. Some examples include:

Limit cycles are important in many scientific applications where systems with self-sustained oscillations are modelled. Some examples include:

极限环在许多自持振荡系统的科学应用中具有重要意义。一些例子包括:

• Aerodynamic limit-cycle oscillations 空气动力学极限环振荡

• The Hodgkin–Huxley model for action potentials in neurons.

神经元 neuron 动作电位 Action Potential的霍奇金-赫胥黎模型 Hodgkin–Huxley model。

• The Sel'kov model of glycolysis.

糖酵解 glycolysis的塞尔科夫模型。

• The daily oscillations in gene expression, hormone levels and body temperature of animals, which are part of the circadian rhythm.

动物基因表达、激素水平和体温的日常变化，这些都是昼夜节律 circadian rhythm的一部分。

• The migration of cancer cells in confining micro-environments follows limit cycle oscillations.

癌细胞 cancer cell在局限微环境中的迁移 migration遵循极限环振荡。

• Some non-linear electrical circuits exhibit limit cycle oscillations, which inspired the original Van der Pol model.

一些非线性电路 electrical circuits表现出极限环振荡，这启发了最初的范德波尔模型 Van der Pol model。

See also

另请参见

• Hyperbolic set 双曲集

• Periodic point 周期点

• Self-oscillation 自我振荡

• Stable manifold 稳定流型

编者推荐

集智文章推荐

什么是非线性系统 | 集智百科

描述变量随时间变化的非线性动力系统与较之简单得多的线性系统相比，可能显得混沌、不可预测或违反直觉。

---

References

参考资料

Further reading

延伸阅读

• Steven H. Strogatz (2014). Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering. Avalon. ISBN 9780813349114. 

• M. Vidyasagar (2002). Nonlinear Systems Analysis (Second ed.). SIAM. ISBN 9780898715262. 

• Philip Hartman, "Ordinary Differential Equation", Society for Industrial and Applied Mathematics, 2002.

• Witold Hurewicz, "Lectures on Ordinary Differential Equations", Dover, 2002.

• Solomon Lefschetz, "Differential Equations: Geometric Theory", Dover, 2005.

• Lawrence Perko, "Differential Equations and Dynamical Systems", Springer-Verlag, 2006.

• Arthur Mattuck, Limit Cycles: Existence and Non-existence Criteria, MIT Open Courseware http://videolectures.net/mit1803s06_mattuck_lec32/#

External links

外部链接

• "limit cycle". planetmath.org. Retrieved 2019-07-06.

Category:Limit sets

类别: 极限集

Category:Nonlinear systems

类别: 非线性系统

Category:Dynamical systems

类别: 动力系统

This page was moved from wikipedia:en:Limit cycle. Its edit history can be viewed at 极限环/edithistory