枢纽
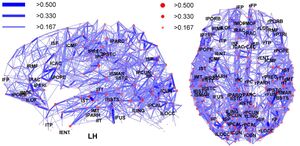
在网络科学中,枢纽 Hub指的是其链接数远超过平均值的节点。网络的无标度性质 Scale-Free Property是枢纽出现的主要原因。[1] 虽然在随机网络中难以观察到枢纽,但它们却有望出现于无标度网络中。无标度网络中枢纽的出现与其幂律分布的性质有关。枢纽对网络的拓扑结构有着重要的影响。我们可以在很多真实的网络中发现枢纽,比如大脑网络或者因特网。
枢纽是拥有大度节点网络的重要构件。与网络中的其他节点相比,枢纽拥有的链接数量明显更多。在保持网络规模N和平均度 <k>不变的情况下,无标度网络中枢纽拥有的链接数(度)远远高于随机网络中链接数最大的节点。枢纽的存在是随机网络和无标度网络的最大区别。在随机网络中,对于每个节点而言,度k是相当的,因此不可能出现枢纽节点。而在无标度网络中,少数节点(即枢纽)具有较高的度值 k,而其他节点则只拥有少量的链接。
涌现
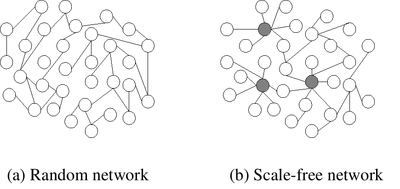
枢纽的涌现可以用无标度网络和随机网络的区别来解释。无标度网络(Barabási-Albert模型)与随机网络 (Erdős–Rényi模型)的区别主要存在于如下两个方面: (a)增长,(b)优先链接。[2]
- (a)无标度网络假设节点数量N保持持续的增长,而随机网络则假设节点数量是固定的。在无标度网络中,最大枢纽的度随着网络规模的增大,呈多项式地上升。因此,在无标度网络中,枢纽的度可以很高。而在随机网络中,最大节点的度随N的增大而呈对数式(或更慢)的上升。因此即使在一个非常大的随机网络中,枢纽的数量也会很小。
- (b)无标度网络中的新节点倾向于链接到度较高的节点,而随机网络中的新节点则与其他节点随机相连。这一过程称为优先链接。新节点链接到度k较高节点的倾向可以用幂律分布来刻画(即,富者越富)。这一想法由维尔弗雷多·帕累托 Vilfredo Pareto提出,它解释了为什么一小部分人赚了大部分的钱。这个过程也存在于网络中,例如80%的网络链接指向15%的网页。无标度网络的出现并不仅仅是人类行为所创造的网络的典型现象,在新陈代谢网络或疾病网络中这一现象也十分常见。[3] 这种现象可以由像Facebook或谷歌这样的万维网枢纽的来解释。这些网页是非常有名的,因此相较于指向随机的小网页,其他网页指向他们的倾向要高得多。
Barabási-Albert模型的数学解释:
网络起始于由[math]\displaystyle{ m_0 }[/math]个节点组成的初始联通网络。
每次向网络添加一个新节点。每个新的节点都被链接到[math]\displaystyle{ m \le m_0 }[/math]个现有的节点,其概率与现有节点已经拥有的链接数量成正比。形式上,新节点与现有节点[math]\displaystyle{ i }[/math]相连的概率[math]\displaystyle{ p_i }[/math]为[2]:
- [math]\displaystyle{ p_i = \frac{k_i}{\sum_j k_j}, }[/math]
其中[math]\displaystyle{ k_i }[/math]是节点[math]\displaystyle{ i }[/math]的度,求和则是针对所有预先存在的节点[math]\displaystyle{ j }[/math]进行的。(分母的数值是网络边数的两倍)。
网络中枢纽的涌现也与时间有关。在无标度网络中,较早出现的节点比后来者更有可能成为枢纽。这种现象被称为先发优势 First-Mover Advantage,它解释了为什么一些节点成为枢纽,而一些没有。然而,在一个真实的网络中,涌现的时间并不是影响枢纽规模的唯一因素。例如,在谷歌成为全球最大互联网枢纽的8年后,Facebook出现了,并于2011年成为了全球最大的互联网枢纽。因此,在实际网络中,枢纽的增长和规模也取决于各种各样的其他属性,如节点的流行程度、质量或老化程度。
属性
无标度网络中的枢纽有诸多属性:
缩短网络路径长度
网络中可观察到的枢纽越多,节点之间的距离就越短。在无标度网络中,枢纽是连接小度节点的桥梁。[4]由于无标度网络中随机节点间的距离很小,我们称无标度网络为“小”或“超小”网络。虽然在一个非常小的网络中,路径长度的差异可能并不明显,但是在大型随机网络和无标度网络中,路径长度的差异是显著的。
无标度网络中的平均路径长度:
- [math]\displaystyle{ \ell\sim\frac{\ln N}{\ln \ln N}. }[/math]
枢纽(节点)的老化
当旧的枢纽被隐藏在网络中时,这种现象便在真实网络中出现。这种现象导致了网络演化和拓扑结构的变化。[5] 老化现象的例子可参照 Facebook 超越了网络中最大的枢纽 Google (自2000年以来最大的节点)。
鲁棒性和抗毁性
当节点发生随机故障或特定攻击时,枢纽是网络的重要构件。当网络中的节点发生随机故障时,枢纽影响网络的鲁棒性。
由于枢纽与大量小度节点共存,随机故障删除枢纽的几率很小。而去除小度节点对网络的完整性影响不大。即使随机删除会作用到上枢纽,网络碎片化 Fragmantation of Network的可能性也非常小,因为剩余的枢纽仍能将网络连接在一起。在这种情况下,枢纽就是无标度网络的中坚力量。
在对枢纽进行特定的攻击时,网络的完整性会相对较快地被破坏。由于小度节点大量的链接到枢纽,因此对最大枢纽的攻击会在短时间内破坏网络。2008年的金融市场崩溃就是这种网络失灵的一个例子,当时头号玩家(枢纽)的破产导致了整个系统的持续崩溃。[6]另一方面,去除恐怖主义网络中的枢纽可能会产生积极的影响,特定节点的消失可能会摧毁整个恐怖组织。网络的抗毁性可以通过连接其外围节点来提高,但是它需要加倍的链接数量。
度相关
完全度相关 Perfect Degree Correlation意味着每个度值为k的节点只链接到相同度值的节点。节点之间的这种链接决定了网络的拓扑结构,从而影响了上文所讨论的网络鲁棒性。如果枢纽之间的链接数量与随机模式下的期望值相同,我们将这个网络称为中性网络 Neutral Network。如果枢纽倾向于相互连接,同时避免链接到小度节点,我们将这个网络称为同配网络 Assortative Network。这种网络的抗毁性相对较强,因为枢纽形成了一个核心团体,这对枢纽的移除来说是更加冗余的。如果枢纽避免相互链接,同时链接到小度节点,我们将这个网络称为异配网络 Disassortative Network。这种网络具有中心辐射特征 Hub-and-Spoke Character。因此,如果我们删除这种类型网络中的枢纽,可能会破坏或摧毁整个网络。
传播现象
枢纽还负责要素在网络上的有效传播。在疾病传播或信息流动的分析中,枢纽被称为超级传播者。超级传播者可能会产生积极的影响,如有效的信息流动,但在H1N1或艾滋病等流行病传播的情况下也会产生毁灭性的影响。如H1H1流行病预测等数学模型,[7]可以基于人类流动网络,传染性,或人与人之间的社会互动,让我们预测疾病的传播。在消灭疾病方面,枢纽也很重要。在无标度网络中,枢纽是最有可能被感染的,因为他们有大量的链接。在枢纽被感染后,它将将疾病传播到它所链接的节点。因此,选择性免疫那些枢纽可能是消灭传播性疾病的成本效率最高的策略。
参考文献
- ↑ Barabási, Albert-László. Network Science: Graph Theory., p. 27
- ↑ 2.0 2.1 Albert R, Barabási AL (2002). "Statistical mechanics of complex networks" (PDF). Reviews of Modern Physics. 74: 47–97. arXiv:cond-mat/0106096. Bibcode:2002RvMP...74...47A. doi:10.1103/RevModPhys.74.47.
- ↑ Barabási, Albert-László. Network Science: The Scale-Free Property., p. 8.[1]
- ↑ Barabási, Albert-László. Network Science: The Scale-Free Property., p. 23.[2]
- ↑ Barabási, Albert-László. Network Science: Evolving Networks., p. 3
- ↑ S. V. Buldyrev; R. Parshani; G. Paul; H. E. Stanley; S. Havlin (2010). "Catastrophic cascade of failures in interdependent networks". Nature. 464 (7291): 1025–28. arXiv:1012.0206. Bibcode:2010Natur.464.1025B. doi:10.1038/nature08932. PMID 20393559.
- ↑ Balcan, Duygu; Hu, Hao; Goncalves, Bruno; Bajardi, Paolo; Poletto, Chiara; Ramasco, Jose J.; Paolotti, Daniela; Perra, Nicola; Tizzoni, Michele; Van den Broeck, Wouter; Colizza, Vittoria; Vespignani, Alessandro (14 September 2009). "Seasonal transmission potential and activity peaks of the new influenza A(H1N1): a Monte Carlo likelihood analysis based on human mobility". BMC Medicine. 7 (45): 29. arXiv:0909.2417. doi:10.1186/1741-7015-7-45. PMC 2755471. PMID 19744314.
编辑推荐
集智课程
图与网络:社交网络分析
社会网络、复杂网络都是复杂性科学研究的热门话题。该课程以「无标度网络」为例,讲解了社交网络及Barabasi-Albert模型,并教学Mathematica中关于网络的一系列工具。
稳健又脆弱的无标度网络
该课程将以无标度网络——复杂网络研究的典型代表为核心,了解复杂网络研究中的不同结构及其特点,现实中的无标度网络和其特点,以及无标度网络正反面效应。
集智文章
本中文词条由Ryan翻译,Alienxj审校,薄荷编辑,如有问题,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。