模拟退火
模拟退火 Simulated annealing SA是一种用于逼近给定函数全局最优值的概率方法。具体来说,它是在大搜索空间中针对优化问题近似全局优化提出的一种元启发法。当搜索空间是离散的(例如旅行商问题)时,经常使用它。对于那些在一定时间内找到一个近似的全局最优解比找到一个精确的局部最优解更重要的问题,模拟退火可能比诸如梯度下降等替代方法更可取。
这个名字和灵感来自于冶金学中的退火,这种技术涉及对材料进行加热和控制冷却以增加其晶体的尺寸并减少其缺陷。两者都是材料的属性,取决于它的热力学自由能。加热和冷却材料都会影响温度和热力学自由能。
模拟退火可以用来逼近具有多个变量的函数的全局最小值。1983年,这种方法被Kirkpatrick, Gelatt Jr.,Vecchi[1]用来解决旅行商问题。他们还提出了它现在的名字----模拟退火。
模拟退火算法中实现缓慢冷却的概念可被理解为探索解决方案空间时接受较差解决方案的概率缓慢下降。由于元启发法允许对全局最优解进行更广泛的搜索,所以接受较差的解可以说是元启发法的一个基本属性。一般来说,模拟退火算法的工作原理如下:温度从最初的正值逐渐降低到零。该算法在每个时间步长上随机选择一个接近当前解的解,测量其质量并根据温度相关的概率选择更好或更坏的解,在搜索过程中分别保持在1(或正值)并向零递减。
可以通过求解密度函数的动力学方程[2][3] 或采用随机抽样方法进行模拟仿真。[1][4] 这种方法是对Metropolis-Hastings算法(一种用于生成热力学系统的样本状态的Monte Carlo方法)的一种改进,该算法在1953年由N. Metropolis等人提出。[5]
概述
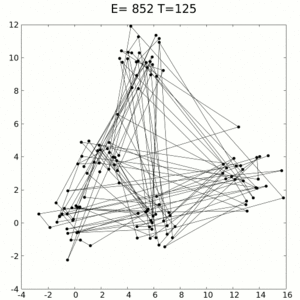
一些物理系统的状态以及最小化函数[math]\displaystyle{ E(S) }[/math]可以看作该状态下系统的内部能量。本算法的目的是让任意初始状态的系统经过变化得到能量最小状态。
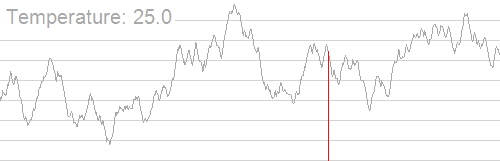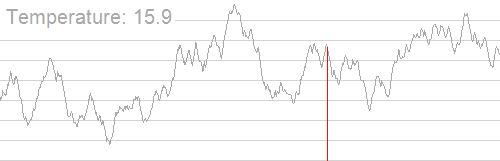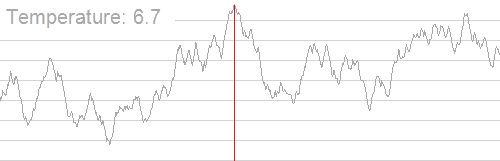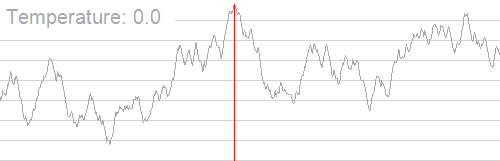
基本迭代
在每个步骤中,模拟退火这种启发式算法都会考虑当前状态[math]\displaystyle{ s }[/math]的某个相邻状态[math]\displaystyle{ s* }[/math],并概率性地决定系统的下一个状态是移至状态[math]\displaystyle{ s* }[/math]还是保持状态[math]\displaystyle{ s }[/math]。这些概率最终会使系统进入能量较低的状态。通常来说需要重复执行迭代步骤,直到系统达到足以满足应用程序的能量状态或耗尽了给定的计算预算。
城市的邻居
解决方案的优化包括评估问题状态的邻居,这些邻居是通过保守改变给定状态而产生的新状态。例如在旅行商问题中,每个地点通常被定义为要访问的城市的排列,通过反转任意两个邻近城市顺序产生邻居的排列集合,不同的移动方式将产生不同的近邻城市集。这种明确界定的改变各地以产生邻近城市集合的方式被称为“移动”。这些移动最后通常会让状态的更改迭代量降到最低,尝试通过迭代改善解决方案的组成部分(例如旅行商问题中的城市联系)来逐步改善解决方案。
像爬山这样的简单启发式方法通过逐步寻找更好的邻居移动,在没有更好邻居处停止,这种方法结果很容易得到局部最优解,而实际最优解可能是有所不同的全局最优解。元启发法为避免陷入局部最优,通过改变选择邻居的方法(即尽管他们更喜欢更好的邻居,但他们也接受更坏的邻居)把解的邻居用作探索解空间。如果运行足够长的时间,这种方法可以找到全局最优值。
接受概率
从当前状态[math]\displaystyle{ s }[/math]到候选状态 [math]\displaystyle{ s' }[/math]的转变概率是由接受概率密度函数[math]\displaystyle{ P(e,e',T) }[/math]确定的,这取决于两个状态的能量[math]\displaystyle{ e = E(s) }[/math] ,[math]\displaystyle{ e' = E(s') }[/math],以及称为温度的全局时变参数[math]\displaystyle{ T }[/math]。能量较小的状态比能量较大的状态好。概率密度函数[math]\displaystyle{ P }[/math]必须是正值,即使[math]\displaystyle{ e' }[/math]大于[math]\displaystyle{ e }[/math],这个特性可以防止陷入比全局最小值糟糕的局部最小值。
当[math]\displaystyle{ T }[/math]趋于零时,如果[math]\displaystyle{ e' \gt e }[/math],概率[math]\displaystyle{ P(e, e', T) }[/math]必须趋于零,反之趋于正值。对于足够小的[math]\displaystyle{ T }[/math]值,系统会越来越倾向于走“下坡路”(即降低能量值) ,而避免走“上坡路”。使用[math]\displaystyle{ T=0 }[/math]的过程,只有下坡过渡,简化为贪婪算法。
在模拟退火的原始描述中,当[math]\displaystyle{ e' \lt e }[/math]时,概率[math]\displaystyle{ P(e, e', T) }[/math]等于1。即无论温度如何,程序总会找到一种方法,找到“下坡路”。许多模拟退火的描述和实现仍然把这个条件作为方法定义的一部分。然而这个条件并不是这个方法工作的必要条件。
The [math]\displaystyle{ P }[/math]函数的选择通常是为了降低接受移动的概率。[math]\displaystyle{ e'-e }[/math]增加意味着小的上坡动作比大的动作更有可能发生。如果符合上述要求,这一要求并非绝对必要。
考虑到这些性质,因为温度[math]\displaystyle{ T }[/math]对系统能量变化很敏感,所以它在控制系统状态[math]\displaystyle{ s }[/math]的演化方面起着至关重要的作用。准确地说,对于一个庞大的[math]\displaystyle{ T }[/math]来说,[math]\displaystyle{ s }[/math]的变化对比粗略的能量变化更为敏感,当[math]\displaystyle{ T }[/math]很小时,它对精细能量变化更为敏感。
退火时间表
算法的名称和灵感需要在算法的运行特性中嵌入一个与温度变化有关的有趣特征,并随着模拟的进行逐渐降低温度。该算法首先将[math]\displaystyle{ T }[/math]设置为一个大值(或无穷大) ,然后按照某种退火时间表(可由用户指定,但必须在分配的时间预算结束时以[math]\displaystyle{ T=0 }[/math]结束)逐步减少。通过这种方式,系统可以按照预期最初在包含良好解的广阔搜索空间游走,忽略能量函数的小特征; 然后向越来越窄的低能量区域漂移; 最后根据梯度下降法启发式向下移动。
对于任何给定的有限问题,随着退火时间表的扩展,模拟退火算法终止于全局最优解的概率接近1。[6] 然而,因为确保取得大概率成功所需的时间通常超过完全搜索解空间所需的时间,所以这一理论结果并不是特别有用。
伪代码
下面的伪代码展示了上面描述的模拟退火启发式代码。它从状态[math]\displaystyle{ s_{0} }[/math]开始,一直持续到已经采取了最多[math]\displaystyle{ k_{max} }[/math]个步骤。在这个过程中,调用[math]\displaystyle{ neighbour(s) }[/math]应该通过随机选择产生一个给定状态为[math]\displaystyle{ s }[/math]的邻居; 调用[math]\displaystyle{ random(0,1) }[/math]应该均匀且随机地选择并返回一个范围在[math]\displaystyle{ [0,1] }[/math]内的值。退火时间表由调用[math]\displaystyle{ temperature(r) }[/math]定义,给定到目前为止所花费的时间预算的分数[math]\displaystyle{ r }[/math],调用该温度来产生要使用的温度。
- Let s = s0
- For k = 0 through kmax (exclusive):
- T ← temperature( (k+1)/kmax )
- Pick a random neighbour, snew ← neighbour(s)
- If P(E(s), E(snew), T) ≥ random(0, 1):
- s ← snew
- Output: the final state s
参数选择
为了将模拟退火算法应用于具体问题,退火过程由冷却进度表 Cooling Schedule 控制,包括控制参数的初值[math]\displaystyle{ t }[/math]及其衰减因子[math]\displaystyle{ Δt }[/math]、每个[math]\displaystyle{ t }[/math]值时的迭代次数[math]\displaystyle{ L }[/math]和停止条件[math]\displaystyle{ S }[/math]。模拟退火算法必须指定以下参数:状态空间、能量(目标)函数 E()、候选生成器过程neighbour()、接受概率函数P()以及退火时刻表和初始温度<init temp>。这些参数的选择能对模拟退火算法的有效性和准确性产生很大的影响。遗憾的是,并没有适用于所有问题的参数选择方法,也没有找到对于给定问题的最佳参数选择的通用方法。下面几节给出一些一般的指导原则。
充分相邻
模拟退火可以建立成一个搜索图上的随机游动模型,其顶点是所有可能的状态,其边是候选移动。对于neighbour()函数的一个基本要求是模拟退火必须提供一条足够短的路径,从初始状态所到达的任何状态都可能是全局最优状态,搜索图的直径必须很小。例如,在上面的旅行推销员示例中,[math]\displaystyle{ n=20 }[/math]个城市的搜索空间有[math]\displaystyle{ n!= 2,432,902,008,176,640,000 }[/math](2.4 亿)个州;然而,每个顶点的邻接数是[math]\displaystyle{ \sum_{k=1}^{n-1} k=\frac{n(n-1)}{2}=190 }[/math]边,图的直径是[math]\displaystyle{ n-1 }[/math]。
跃迁概率
为了研究模拟退火在特定问题上的行为,考虑算法实现过程中的各种设计选择所产生的跃迁概率是很有用的。对于搜索图的每条边[math]\displaystyle{ (s,s') }[/math],跃迁概率定义为模拟退火算法在当前状态[math]\displaystyle{ s' }[/math] </math> s</math>时移动到状态[math]\displaystyle{ s' }[/math]的概率。此概率取决于指定的当前温度、temperature()函数生成候选移动的顺序以及接受概率P()函数。注意,跃迁概率不是简单地[math]\displaystyle{ P(e, e', T) }[/math],因为候选对象是连续进行测试的。
接受概率
neighbour(), P()和temperature()的规范部分是多余的。在实际应用中,对许多问题使用相同的验收函数,并根据具体问题对其他两个函数进行调整,这是很常见的。
在Kirkpatrick等人的方法中,如果[math]\displaystyle{ e' \lt e }[/math], [math]\displaystyle{ \exp(-(e'-e)/T) }[/math],则接受概率函数[math]\displaystyle{ P(e, e', T) }[/math]定义为1。这一公式实际上是通过类比物理系统的变迁而得到证明的;在T=1且建议分布对称的情况下,对应于Metropolis-Hastings算法。然而,这个接受概率经常被用于模拟退火算法,甚至当函数(类似于Metropolis-Hastings中的建议分布)不是对称的,或者根本不是概率性的时候也是如此。
因此,模拟退火算法的跃迁概率并不对应于类似物理系统的跃迁概率,并且,在恒温[math]\displaystyle{ T }[/math]状态下的长期分布与物理系统在任何温度下状态上的热力学平衡分布并不相似。
然而,大多数关于模拟退火的描述都假定了最初的接受函数,这使得可能在SA的许多实现中都是硬编码 hard-coded的。硬编码指“将可变变量用一个固定数值表示”,这种方式在编码的过程中会导致变量很难修改。
1990年,莫斯卡托 Moscato 和丰塔纳里 Fontanari[7]提出确定性更新(即不基于概率接受规则的更新),其可以在不影响最终质量的情况下加快优化过程。Moscato和Fontanari通过观察源自他们的研究的类似于“阈值更新”退火的“比热”曲线得出结论:“模拟退火算法中的Metropolis更新的随机性在寻找近似最优最小值中没有发挥主要作用”。相反,他们提出“在高温下平滑成本函数景观和在冷却过程中逐渐定义最小值是模拟退火成功的基本要素。”这种方法后来被Dueck和Scheuer命名为“阈值接受”而推广开来。
在2001年,Franz, Hoffmann和Salamon证明了确定性更新策略确实是在模拟成本/能量趋势图上随机行走的大类算法中最优的。[8].
有效的备选
在选择候选产生器 neighbour()时,必须考虑到经过模拟退火算法的多次迭代后,当前状态的能量比随机状态低得多。因此,通常的规则是,当目标状态[math]\displaystyle{ s' }[/math]的能量可能与当前状态类似时,应该使生成器向候选的地方移动倾斜。这种启发式(这是Metropolis-Hastings算法的主要原则)倾向于排除“非常好的”候选移动和“非常糟糕的”候选移动;然而,前者通常比后者少得多,所以启发式通常是相当有效的。
例如,在上面的旅行商问题中,也就是TSP问题(Traveling Salesman Problem)。假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。在一个寻找最短路径的旅行中,对两个连续的城市所走的顺序进行交换,预计会对其能量(长度)产生适度的影响;而交换两个任意的城市的移动顺序更有可能增加而不是减少城市的长度。因此,预期连续交换邻接生成器的性能要优于任意交换生成器,尽管后者可以提供更短的路径来达到最佳状态(使用[math]\displaystyle{ n-1 }[/math]交换,而不是[math]\displaystyle{ n(n-1)/2 }[/math])。
关于这种启发式的一个更精确的陈述是,人们应该尝试第一个候选状态的数学 s / math,对于这个状态的数学 p (e (s) ,e (s’) ,t) / math 是很大的。对于上面提到的“标准”接受函数数学 p / math,它意味着数学 e (s’)-e (s) / math 的顺序是数学 t / math 或更少。因此,在上面的旅行推销员的例子中,我们可以使用一个交换两个随机城市的函数,其中选择一个城市对的概率消失了,因为它们的距离增加超过了数学 t / math。
一个更精确的启发式陈述是,我们应该尝试第一个候选状态[math]\displaystyle{ s' }[/math],其中[math]\displaystyle{ P(E(s), E(s'), T) }[/math]很大。对于上面的“标准”接受函数[math]\displaystyle{ P }[/math],这意味着[math]\displaystyle{ E(s') - E(s) }[/math]的长度是[math]\displaystyle{ T }[/math]或更少。因此,在上面的旅行商问题中,我们可以使用一个函数来交换两个随机城市,当它们的距离超过[math]\displaystyle{ T }[/math]时,就不再选择该城市对。
避障
在选择候选生成器时,还必须尝试减少具有比所有相邻状态低得多的能量的“深层”局部最小状态(或连接状态集)的数量。这种局部优解的聚集相当于在解空间形成了“盆地”,使得对应的能量函数可能以很高的概率(大致与盆地内的状态数成正比)并在很长一段时间内(大致以周围状态与盆地底部的能量差的指数形式反映)困住模拟退火算法。
一般来说,不可能设计一个候选生成器,既能满足这个目标,又能优先考虑具有类似能量的候选移动。另一方面,通过对生成器进行相对简单的更改,可以极大地提高模拟退火的效率。例如在旅行商问题中,不难看出旅行[math]\displaystyle{ A }[/math], [math]\displaystyle{ B }[/math]有着近似相等的长度:
- [math]\displaystyle{ A }[/math]处最优;
- 从[math]\displaystyle{ A }[/math]到[math]\displaystyle{ B }[/math]的每个城市对相互转换,经过更长的旅程
- 通过翻转(颠倒顺序)一系列连续的城市[math]\displaystyle{ A }[/math]可以转换成[math]\displaystyle{ B }[/math]。
在这个例子中,如果生成器只执行随机的对交换,[math]\displaystyle{ A }[/math]和[math]\displaystyle{ B }[/math]位于不同的“深盆”中;但是,如果生成器执行随机段翻转,它们将处于相同的池中。
冷却时刻表
用来证明模拟退火合理性的物理类比是假定冷却速率足够低,使当前状态的概率分布在任何时候都接近热力学平衡。遗憾的是,弛豫时间——一个人必须等待平衡在温度变化后恢复的时间——强烈地依赖于能量函数的“地形”和当前的温度。在模拟退火算法中,弛豫时间也以非常复杂的方式依赖于候选生成器。注意,所有这些参数通常都作为黑盒函数提供给模拟退火算法。因此,理想的冷却速率不能预先确定,应该根据实际情况对每个问题进行调整。自适应模拟退火算法通过将冷却计划与搜索过程相结合来解决这个问题。其他自适应方法如热力模拟退火[9],根据美国热力学定律协会的说法,可以根据两种状态之间的能量差自动调节每一步的温度。
重新启动Restarts
有时候,回到一个比总是从当前状态移动更好的解决方案,而不是总是从当前状态移动。这个过程被称为模拟退火的重新启动。为此,我们将s和e 设置为sbest和ebest并可能重新启动退火时刻表。重新启动的决定可能基于几个标准。其中值得注意的有:基于固定步数的重启,基于当前能量是否高于目前获得的最佳能量,随机重启等。
相关算法
- 交互Metropolis–Hasting算法(又名顺序蒙特卡罗算法)[10]结合模拟退火算法,采用交互循环机制,对最适合的个体进行接受-拒绝。
- 量子退火 Quantum annealing使用“量子涨落 quantum fluctuations”而不是热涨落来穿过目标函数中高而薄的屏障。
- 随机隧穿 Stochastic tunneling尝试克服模拟退火运行在温度降低时从局部极小值逃逸的困难,通过“隧穿”通过障碍。
- 禁忌搜索 Tabu search通常会移动到能量较低的邻近状态,但当它发现自己陷入局部极小值时,就会向上移动;并通过保留已经看到的解决方案的“禁忌列表”来避免循环。
- 双阶段进化 Dual-phase evolution是一系列的算法和进程(模拟退火所属),它们通过利用搜索空间中的相位变化在局部搜索和全局搜索之间进行协调。
- 反应式搜索优化 Reactive search optimization侧重于将机器学习与优化结合起来,通过添加一个内部反馈回路,自调整算法的自由参数,根据问题、实例,去适应当前解决方案周围的局部情况。
- 随机梯度下降法 Stochastic gradient descent从随机初始点开始进行许多贪婪搜索。
- 遗传算法 Genetic algorithms 保持了一个解决方案池,而不仅仅是一个新的候选解决方案不仅可以通过“突变”(如SA)生成,还可以通过从池中“重新组合”两个解决方案生成。 与 SA 中使用的概率标准类似,用于选择突变或组合的候选方案,并从池中剔除多余的解。
- 模因算法 Memetic algorithms通过雇佣一组在过程中既合作又竞争的代理人来寻找解决方案;有时,代理商的策略包括模拟退火程序,以获得高质量的解决方案,再进行重新组合。[11] 模拟退火也被认为是一种增加搜索多样性的机制。[12]
- 逐步优化 Graduated optimization就是在优化时对目标函数进行“平滑”处理。
- 蚁群优化 Ant colony optimization(ACO)使用许多蚂蚁(或代理)遍历解空间,寻找局部生产区域。
- 交叉熵方法 cross-entropy method (CE)通过参数化的概率分布生成候选解。通过交叉熵最小化对参数进行更新,以便在下一次迭代中生成更好的样本。
- 和声搜索 Harmony search 模仿音乐家在即兴创作的过程中,每个音乐家演奏一个音符以找到最好的和声。
- 随机优化 Stochastic optimization是一系列包括模拟退火和许多其他方法的算法集合。
- 粒子群优化 Particle swarm optimization是一种以群体智能为模型的算法,它可以在搜索空间中找到优化问题的解决方案,或者在目标存在的情况下对社会行为进行建模和预测。
- 分枝根算法 The runner-root algorithm (RRA)是一种元启发式优化算法,用于解决单峰和多峰问题,是由自然植物的生长和根启发而来。
- 智能水滴算法 Intelligent water drops algorithm (IWD)模仿自然水滴的行为来解决优化问题。
- 并行退火 Parallel tempering是模拟模型副本在不同温度(或汉密尔顿)下克服潜在障碍的过程。
另请参阅
- 自适应模拟退火
- 马尔可夫链 Markov chain
- 组合优化 Combinatorial optimization
- 双相演化 Dual-phase evolution
- 自动标签位置 Dual-phase evolution
- 多学科优化 Multidisciplinary optimization
- 地点和路线 Place and route
- 分子动力学 Molecular dynamics
- 旅行商问题 Traveling salesman problem
- 计算机视觉中的图形切割
- 粒子群优化 Particle swarm optimization
- 智能水滴算法 Intelligent water drops algorithm
参考文献
- ↑ 1.0 1.1 Kirkpatrick, S.; Gelatt Jr, C. D.; Vecchi, M. P. (1983). "Optimization by Simulated Annealing". Science. 220 (4598): 671–680. Bibcode:1983Sci...220..671K. CiteSeerX 10.1.1.123.7607. doi:10.1126/science.220.4598.671. JSTOR 1690046. PMID 17813860.
- ↑ Khachaturyan, A.; Semenovskaya, S.; Vainshtein, B. (1979). "Statistical-Thermodynamic Approach to Determination of Structure Amplitude Phases". Sov.Phys. Crystallography. 24 (5): 519–524.
- ↑ Khachaturyan, A.; Semenovskaya, S.; Vainshtein, B. (1981). "The Thermodynamic Approach to the Structure Analysis of Crystals". Acta Crystallographica. 37 (A37): 742–754. Bibcode:1981AcCrA..37..742K. doi:10.1107/S0567739481001630.
- ↑ Černý, V. (1985). "Thermodynamical approach to the traveling salesman problem: An efficient simulation algorithm". Journal of Optimization Theory and Applications. 45: 41–51. doi:10.1007/BF00940812.
- ↑ Metropolis, Nicholas; Rosenbluth, Arianna W.; Rosenbluth, Marshall N.; Teller, Augusta H.; Teller, Edward (1953). "Equation of State Calculations by Fast Computing Machines". The Journal of Chemical Physics. 21 (6): 1087. Bibcode:1953JChPh..21.1087M. doi:10.1063/1.1699114.
- ↑ Granville, V.; Krivanek, M.; Rasson, J.-P. (1994). "Simulated annealing: A proof of convergence". IEEE Transactions on Pattern Analysis and Machine Intelligence. 16 (6): 652–656. doi:10.1109/34.295910.
- ↑ Dueck, G.; Scheuer, T. (1990), "Threshold accepting: A general purpose optimization algorithm appearing superior to simulated annealing", Journal of Computational Physics, 90 (1): 161–175, doi:10.1016/0021-9991(90)90201-B, ISSN 0021-9991
- ↑ Franz, A.; Hoffmann, K.H.; Salamon, P, "Best optimal strategy for finding ground states", Physical Review Letters, 86 (3): 5219–5222, doi:10.1103/PhysRevLett.86.5219
- ↑ De Vicente, Juan; Lanchares, Juan; Hermida, Román (2003). "Placement by thermodynamic simulated annealing". Physics Letters A. 317 (5–6): 415–423. Bibcode:2003PhLA..317..415D. doi:10.1016/j.physleta.2003.08.070.
- ↑ Del Moral, Pierre; Doucet, Arnaud; Jasra, Ajay (2006). "Sequential Monte Carlo samplers - P. Del Moral - A. Doucet - A. Jasra - 2006 - Journal of the Royal Statistical Society: Series B (Statistical Methodology) - Wiley Online Library". Journal of the Royal Statistical Society, Series B. 68 (3): 411–436. arXiv:cond-mat/0212648. doi:10.1111/j.1467-9868.2006.00553.x.
- ↑ Moscato, Pablo (June 1993). "An introduction to population approaches for optimization and hierarchical objective functions: A discussion on the role of tabu search". Annals of Operations Research. 41 (2): 85–121. doi:10.1007/BF02022564.
- ↑ Moscato, P. (1989). "On Evolution, Search, Optimization, Genetic Algorithms and Martial Arts: Towards Memetic Algorithms". Caltech Concurrent Computation Program (report 826).
进一步阅读
- A. Das and B. K. Chakrabarti (Eds.), Quantum Annealing and Related Optimization Methods, Lecture Note in Physics, Vol. 679, Springer, Heidelberg (2005)
- 达斯与查克拉巴蒂(合编) ,量子退火和相关的优化方法,物理学讲义,第 679卷。斯普林格,海德保(2005)
- Weinberger, E. (1990). "Correlated and uncorrelated fitness landscapes and how to tell the difference". Biological Cybernetics. 63 (5): 325–336. doi:10.1007/BF00202749.
- 温伯格(1990)。 “相关和不相关的适应度分布以及如何区分差异”。 生物控制论。 63(5) : 325-336. 10.1007 / BF00202749.
--趣木木(讨论)困惑于健身景观
- Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007). "Section 10.12. Simulated Annealing Methods". Numerical Recipes: The Art of Scientific Computing (3rd ed.). New York: Cambridge University Press. ISBN 978-0-521-88068-8. http://apps.nrbook.com/empanel/index.html#pg=549.
- 出版社:WH; Teukolsky,SA; Vetterling,WT; Flannery,BP (2007)。 “第10.12条。 模拟退火方法”。 科学计算的艺术(第三版) . 纽约: 剑桥大学出版社。 国际标准图书编号978-0-521-88068-8。
- Strobl, M.A.R.; Barker, D. (2016). "On simulated annealing phase transitions in phylogeny reconstruction". Molecular Phylogenetics and Evolution. 101: 46–55. doi:10.1016/j.ympev.2016.05.001. PMC 4912009. PMID 27150349.
- 斯特罗布,m.a.r. ; 巴克,d. (2016)。 关于系统发展重建中的模拟退火阶段转换。 分子系统发育与进化期刊。 101:46-55. 10.1016 / j.ympev. 2016.05.001. 4912009. 27150349.
- V.Vassilev, A.Prahova: "The Use of Simulated Annealing in the Control of Flexible Manufacturing Systems", International Journal INFORMATION THEORIES & APPLICATIONS, VOLUME 6/1999
- V. vassilev,A.Prahova: “模拟退火在柔性制造系统控制中的应用” ,《国际信息理论与应用》 ,1999年第6卷
其他链接
- 模拟退火的一个Javascript应用程序,允许实验模拟退火。包括源代码。
- “通用模拟退火算法”是一个用于通用模拟退火练习的开源MATLAB程序。
- 模拟退火的自我指导课程维基学院项目。
- 谷歌在叠加使用、不使用量子计算机的Ars技术中讨论了谷歌所使用的D波计算机可能实际上是一个高效的模拟退火协处理器的可能性。
编者推荐
书籍推荐
- 肖柳青、周石鹏编著的《随机模拟方法与应用》力图以通俗易懂与自封的方式叙述随机模拟方法,通过大量生活中的实例来阐明模拟的基本方法与相关概念,并给出全部例子的Matlab程序。全书共分十一章,分别介绍了随机模拟方法的特点与步骤、概率论预备知识、Matlab软件的基本编程方法、随机数的生成方法、马尔可夫链蒙特卡罗方法、随机服务系统模型、蒙特卡罗优化方法、随机游走模型、蒙特卡罗积分方法、复杂系统的模拟。其中应用方面涉及了经济金融、统计物理、排队论、交通流、社会问题及其复杂网络等问题。
文章推荐
- 量子机器学习不知不觉已经进入1.0时代了。这个如此让人兴奋的新领域,不仅可以帮助我们更好地进行机器学习,还有助于我们对机器学习进行创新,甚至重新定义我们对于机器学习的思考方式。
- 这篇文章介绍了模拟退火的基本知识并附有MATLAB代码。
- 网络的分解不仅对结构勘探有用。它们在给定网络上运行的过程的分析和计算解决方案(如伊辛模型、渗透模型、SIR模型)中也有应用。这里考虑的树和分支分解直接将网络结构表示为树,用于网络属性的递归计算。与基于群落结构或元结构的粗粒化近似不同,足够小宽度的树分解允许在平衡过程中得到精确的结果。在这里,作者使用模拟退火来寻找一组中等规模经验网络的窄宽度树分解。但并没有直接优化树的分解,而是使用了一个搜索空间,这个搜索空间由所谓的消除顺序构成,也就是网络节点集上的排列。
课程推荐
- 在这节课中,首先会复习上节课学习的内容,即群体系统与群体思维的应用。然后,会介绍什么是涌现。在讲解涌现的时候会引出“Pattern”这个概念,即人类是如何凭着自己的主观视角,无中生有,识别出所谓的模式的。并可以学习:群集思维的应用方法,如蚁群算法、粒子群优化算法、粘菌的智慧、N皇后问题等。
本中文词条由沐晨、趣木木用户参与编译,乐多多编辑,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。