演化算法 Evolutionary Algorithms
在计算智能 computational intelligence 领域,演化算法(EA)(或称进化算法)是演化计算的子集[1] ,是一种基于群体的元启发式最优化算法。演化算法使用到了各种模拟生物演化机制的操作,比如繁衍、变异、重组、选择等。在群体中每一个个体都是问题的备选解,而适应度函数 fitness function用于计算出每一个解的质量(亦即个体对于环境的适应度)。演化就是在不断在群体中进行繁衍、变异、重组、选择这些操作进而找出最优解的过程。
演化算法通常会对各种优化问题得出很好的近似解,因为演化算法不会做出任何假设,对每一个问题都一视同仁。演化算法通常应用于求解最优化问题,在生物建模方面一般来说只会用在基于细胞过程的微观演化过程和规划模型研究中。在大多数演化算法的应用中,计算复杂度都是最大的障碍[2]。事实上,这种计算复杂度来源于适应度函数。适应度近似法 fitness approximation是克服这一障碍的方法之一。但看似简单的演化算法经常能够解决复杂的问题,因此,算法的复杂度应该与问题的复杂度没有直接关系。
实现
第一步:随机生成第一代群体。
第二步:重复下面各步直到满足中止条件:
- 计算群体中每个个体的适应度
- 选择适应度最高个体进行繁衍操作。
- 对于繁衍下来的新个体进行重组和变异操作,以得到后代。
- 计算新个体的适应度。
- 淘汰掉群体中适应度低的个体。
类型
演化算法的具体技术可以按照遗传信息表达方式、实现细节、以及特定问题的特定处理分类。
- 遗传算法 Genetic algorithm:这是演化算法中最常用的类型。这种技术应用于求解最优解是一组数字的问题。
- 遗传编程 Genetic programming :这种技术用于生成一段计算机程序,其适应度就是这些计算机程序解决某计算问题的能力,具体案例可以参考使用pythony实现遗传算法。
- 演化编程 Evolutionary programming :与遗传编程类似,但其求解的计算机程序的结构是固定的,可以演化的是一些数值参数。
- 基因表达编程 Gene expression programming :类似于遗传编程,基因表达规划同样以计算机程序群体来进行演化计算,但这种计算机程序虽然大小不同,却都编码在相同固定的线性染色体中。
- 演化策略 Evolution strategy :这种技术以实数向量作为个体,而且使用了自适应的变异率。
- 差分演化 Differential evolution :这种算法以向量的差为基础,因此特别适合数值最优化问题。
- 神经演化 Neuroevolution:类似于遗传编程,但是基因组表示的是人工神经网络的结构和连接权重,这种基因组编码可以是直接编码也可以是间接编码。
- 学习分类器系统 Learning classifier system :这种技术的解是一组分类器(规则或条件)。密歇根-学习分类器系统 Michigan-LCS在个体层面进行演化,而匹兹堡-学习分类器系统 Pittsburgh-LCS则使用分类器集合群体来演化。最开始的时候这些分类器都是0-1编码的,如今包含实数、神经网络、或者S-expression。其适应度一般是分类器系统应用于强化学习或有监督学习时的准确率。
与生物过程的比较
对于演化算法来说,一个可能的局限可能是缺少对基因型和表现型的明确区分。在大自然中,一个受精卵会历经一个成为胚胎发育的过程,然后成为一个成熟的表现型。自然选择以表现型而非基因型为选择标准。这种间接编码被认为可以使得演化过程更健壮(降低致命突变的概率),并提高器官的进化能力[3][4] 。这种间接编码还使得演化能够充分利用环境的规律[5]。最近有关人工胚胎学 artificial embryogeny 和人工发展系统 artificial developmental system 的工作也在寻求解决这一局限的方法。基因表达规划这一技术在基因型-表现型系统的探索中取得成功,其中基因型包括固定长度地线性多基因染色体,而表现型则包括了规模可变的多重表达式树或者计算机程序[6]。
相关技术
群算法包括:
- 蚁群优化算法:这种技术以蚂蚁觅食和通过信息素沟通寻路为基础,最早应用于组化优化和图相关问题。
- 茎根算法 runner-root algorithm:一种受自然中植物的茎和根的功能启发的算法。[7]
- 人工蜂群算法 Artificial bee colony algorithm:根据蜜蜂觅食行为设计,最初为数值优化提出,后来扩展至解决组合、受约束的多目标最优化问题。
- 布谷鸟搜索 Cuckoo search:根据布谷鸟巢寄生的行为提出,同时使用了 Lévy flights 机制,因此适用于全局最优化问题。
- 电子优化算法:这种技术背后的思想是电子流经电路时根据最小电阻原则分流的原理。[8]
- 粒子群算法:是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法,最适合用于解决数值优化问题。
其他基于群体的元启发式方法
- 狩猎搜索 Hunting Search :根据自然中地狩猎行为提出,一群捕食者,如狼群,组织他们的位置来包围猎物。捕食者中每一个个体的位置会根据其他个体,尤其是领袖的位置调整。这是一个连续型优化方法[9],后改进为组合优化方法[10]。
- 适应性维度搜索 Adaptive dimensional search :不同于仿生元启发式技术,适应性维度搜索没有模仿任何大自然中的现象。它使用简单的性能导向方法,每一次迭代过程都会更新搜索维度率 search dimension ratio 。[11]。
- 萤火虫算法 Firefly algorithm:通过模仿萤火虫发光互相吸引的行为设计,特别适用于多峰函数的最优化求解。
- 和弦搜索 Harmony search :基于音乐家探索更好的和弦的因为提出,适用于组合优化和参数优化。
- 高斯适应 Gaussian adaptation :一种基于信息论的方法, 用于最大化成品率、平均适应度、平均信息量等。参考热力学和信息论中的熵
- 模因算法 Memetic algorithm:这是一种混合方法,根据理查德·道金斯的模因 meme概念提出。这通常在基于群体的算法中,给每一个个体加入学习行为使得他们可以进行局部优化。这种方法强调利用每个问题自身的特性,并调和局部和全局搜索。
- 帝企鹅群:一种受帝企鹅群的行为启发的方法。在群体中的帝企鹅会产生适应的热量并调整自身的体温,这种热量只受每只企鹅的移动来调整和控制。[12]
案例
- 2020年,Google宣布他们的AutoML-Zero成功重复发现了一些经典的算法,比如神经网络[13]。
- 计算机模拟程序Tierra和Avida尝试性地对宏观进化过程的动力学建模。
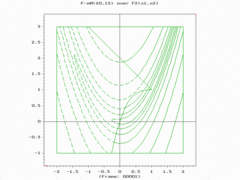
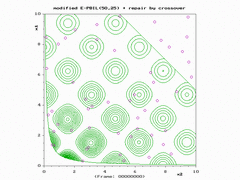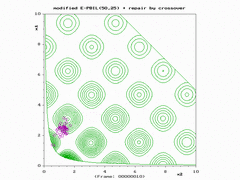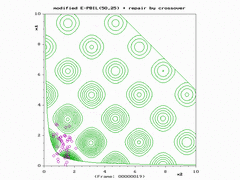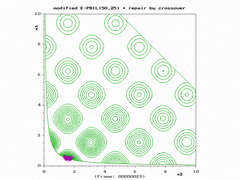
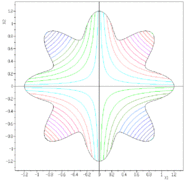
模拟结果展示
参考文献
- ↑ Vikhar, P. A. (2016). "Evolutionary algorithms: A critical review and its future prospects". Proceedings of the 2016 International Conference on Global Trends in Signal Processing, Information Computing and Communication (ICGTSPICC). Jalgaon. pp. 261–265. doi:10.1109/ICGTSPICC.2016.7955308. ISBN 978-1-5090-0467-6.
- ↑ Cohoon, J (2002-11-26). Evolutionary algorithms for the physical design of VLSI circuits. Springer, pp. 683-712, 2003. ISBN 978-3-540-43330-9. https://www.ifte.de/mitarbeiter/lienig/cohoon.pdf.
- ↑ G.S. Hornby and J.B. Pollack. "Creating high-level components with a generative representation for body-brain evolution". Artificial Life, 8(3):223–246, 2002.
- ↑ Jeff Clune, Benjamin Beckmann, Charles Ofria, and Robert Pennock. "Evolving Coordinated Quadruped Gaits with the HyperNEAT Generative Encoding" . Proceedings of the IEEE Congress on Evolutionary Computing Special Section on Evolutionary Robotics, 2009. Trondheim, Norway.
- ↑ J. Clune, C. Ofria, and R. T. Pennock, "How a generative encoding fares as problem-regularity decreases", in PPSN (G. Rudolph, T. Jansen, S. M. Lucas, C. Poloni, and N. Beume, eds.), vol. 5199 of Lecture Notes in Computer Science, pp. 358–367, Springer, 2008.
- ↑ Ferreira, C., 2001. "Gene Expression Programming: A New Adaptive Algorithm for Solving Problems". Complex Systems, Vol. 13, issue 2: 87–129.
- ↑ F. Merrikh-Bayat, "The runner-root algorithm: A metaheuristic for solving unimodal and multimodal optimization problems inspired by runners and roots of plants in nature", Applied Soft Computing, Vol. 33, pp. 292–303, 2015
- ↑ Khalafallah Ahmed; Abdel-Raheem Mohamed (2011-05-01). "Electimize: New Evolutionary Algorithm for Optimization with Application in Construction Engineering". Journal of Computing in Civil Engineering. 25 (3): 192–201. doi:10.1061/(ASCE)CP.1943-5487.0000080.
- ↑ Oftadeh, R.; Mahjoob, M.J.; Shariatpanahi, M. (October 2010). "A novel meta-heuristic optimization algorithm inspired by group hunting of animals: Hunting search". Computers & Mathematics with Applications. 60 (7): 2087–2098. doi:10.1016/j.camwa.2010.07.049.
- ↑ Amine Agharghor; Mohammed Essaid Riffi (2017). "First Adaptation of Hunting Search Algorithm for the Quadratic Assignment Problem". Europe and MENA Cooperation Advances in Information and Communication Technologies. Advances in Intelligent Systems and Computing. 520: 263–267. doi:10.1007/978-3-319-46568-5_27. ISBN 978-3-319-46567-8.
- ↑ Hasançebi, O., Kazemzadeh Azad, S. (2015), "Adaptive Dimensional Search: A New Metaheuristic Algorithm for Discrete Truss Sizing Optimization", Computers and Structures, 154, 1–16.
- ↑ Harifi, Sasan; Khalilian, Madjid; Mohammadzadeh, Javad; Ebrahimnejad, Sadoullah (25 February 2019). "Emperor Penguins Colony: a new metaheuristic algorithm for optimization". Evolutionary Intelligence. 12 (2): 211–226. doi:10.1007/s12065-019-00212-x.
- ↑ Gent, Edd (13 April 2020). "Artificial intelligence is evolving all by itself". Science | AAAS (in English). Archived from the original on 16 April 2020. Retrieved 16 April 2020.
- ↑ Simionescu, P.A.; Beale, D.G.; Dozier, G.V. (2004). "Constrained optimization problem solving using estimation of distribution algorithms" (PDF). Proc. of the 2004 Congress on Evolutionary Computation - CEC2004. Portland, OR: 1647–1653. doi:10.1109/CEC.2006.1688506. Retrieved 7 January 2017.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ Simionescu, P.A.; Dozier, G.V.; Wainwright, R.L. (2006). "A Two-Population Evolutionary Algorithm for Constrained Optimization Problems". 2006 IEEE International Conference on Evolutionary Computation. Proc 2006 IEEE International Conference on Evolutionary Computation. Vancouver, Canada. pp. 1647–1653. doi:10.1109/CEC.2006.1688506. ISBN 0-7803-9487-9. http://faculty.tamucc.edu/psimionescu/PDFs/WCCI2006-Paper7204(1).pdf.
- ↑ Simionescu, P.A. (2014). Computer Aided Graphing and Simulation Tools for AutoCAD Users (1st ed.). Boca Raton, FL: CRC Press. ISBN 978-1-4822-5290-3.
其他参阅
- Ashlock, D. (2006), Evolutionary Computation for Modeling and Optimization, Springer, ISBN 0-387-22196-4.
- Bäck, T. (1996), Evolutionary Algorithms in Theory and Practice: Evolution Strategies, Evolutionary Programming, Genetic Algorithms, Oxford Univ. Press.
- Bäck, T., Fogel, D., Michalewicz, Z. (1997), Handbook of Evolutionary Computation, Oxford Univ. Press.
- Banzhaf, W., Nordin, P., Keller, R., Francone, F. (1998), Genetic Programming - An Introduction, Morgan Kaufmann, San Francisco
- Eiben, A.E., Smith, J.E. (2003), Introduction to Evolutionary Computing, Springer.
- Holland, J. H. (1992), Adaptation in Natural and Artificial Systems, The University of Michigan Press, Ann Arbor
- Michalewicz Z., Fogel D.B. (2004). How To Solve It: Modern Heuristics, Springer.
- Benko, Attila; Dosa, Gyorgy; Tuza, Zsolt (2010). "Bin Packing/Covering with Delivery, solved with the evolution of algorithms". 2010 IEEE Fifth International Conference on Bio-Inspired Computing: Theories and Applications (BIC-TA). pp. 298–302. doi:10.1109/BICTA.2010.5645312. ISBN 978-1-4244-6437-1.
- Poli, R.; Langdon, W. B.; McPhee, N. F. (2008). A Field Guide to Genetic Programming. Lulu.com, freely available from the internet. ISBN 978-1-4092-0073-4. http://cswww.essex.ac.uk/staff/rpoli/gp-field-guide/.[self-published source]
- Price, K., Storn, R.M., Lampinen, J.A., (2005). "Differential Evolution: A Practical Approach to Global Optimization", Springer.
- Ingo Rechenberg (1971): Evolutionsstrategie - Optimierung technischer Systeme nach Prinzipien der biologischen Evolution (PhD thesis). Reprinted by Fromman-Holzboog (1973).
- Hans-Paul Schwefel (1974): Numerische Optimierung von Computer-Modellen (PhD thesis). Reprinted by Birkhäuser (1977).
- Simon, D. (2013): Evolutionary Optimization Algorithms, Wiley.
- Computational Intelligence: A Methodological Introduction by Kruse, Borgelt, Klawonn, Moewes, Steinbrecher, Held, 2013, Springer.
- Rahman, Rosshairy Abd.; Kendall, Graham; Ramli, Razamin; Jamari, Zainoddin; Ku-Mahamud, Ku Ruhana (2017). "Shrimp Feed Formulation via Evolutionary Algorithm with Power Heuristics for Handling Constraints". Complexity. 2017: 1–12. doi:10.1155/2017/7053710.
集智推荐
文章推荐
人工生命全景图:如何创造出超越人工智能的生命系统
该文章是对Lana Sinapayen的《Introduction to Artificial Life for People who Like AI》一文进行的总结,主要从研究目标、发展历史、与人工智能的关系等方面对人工生命进行了介绍。
基于垫脚石原理的神经演化算法:为人工智能注入创造力
该文章主要介绍了计算机科学家 Kenneth Stanley提出的基于垫脚石原理的神经演化算法。
课程推荐
颠覆式创新与AI发展前沿追踪
课程简介:本课程主要介绍了当前人工智能在社会领域的应用及优化,包括人工智能在智能零售、机器人、图片超分辨率、机器翻译,以及复杂网络领域的应用。除此之外还介绍了在新时代中,中国创新的的崛起。
时间与进化
课程简介:本课程将站在时间这个角度去从物理学、热力学、生物学的不同领域进行解释和探索,并介绍一些关于遗传算法的相关计算机模拟实例,来帮助我们从多视角看待时间与进化。本课程将站在时间这个角度去从物理学、热力学、生物学的不同领域进行解释和探索,并介绍一些关于遗传算法的相关计算机模拟实例,来帮助我们从多视角看待时间与进化。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。