热力学第二定律
热力学第二定律 Second law of thermodynamics指出,孤立系统 isolated system的总熵永远不会随着时间而减少,且当且仅当所有过程都是可逆时,总熵才恒定。[1]孤立系统自发地向热力学平衡发展,即具有最大熵时的状态。
系统及其周围环境的总熵在理想情况下可以保持不变,在这种情况下,系统处于热力学平衡状态,或者正在经历一个假想的可逆过程。所有过程中,包括自发过程 spontaneous processes,es,[2] 系统及其周围环境的总熵增加,这一过程在热力学意义上是不可逆的。熵的增加解释了自然过程的不可逆性,以及未来和过去之间的不对称性[3]
从历史上看,第二定律是一个经验性的发现,它被认为是热力学理论中的公理。经典统计力学、量子统计力学都可以解释这个定律的微观起源。
热力学第二定律可以使用多种方法表述。它的第一个公式归功于法国科学家萨迪·卡诺 Sadi Carnot,Carnot在1824年证明了在热机中将热转化为功的效率有一个上限。第二定律的这个方面也被称为卡诺规则 Carnot's Rule或卡诺限制 Carnot's Limit。[4]
热力学第二定律也是热力学的四条基本定律之一,它表述了热力学过程的不可逆性——孤立系统自发地朝着热力学平衡方向(即最大熵状态)演化,另一种表述为:第二类永动机永不可能实现。
简介
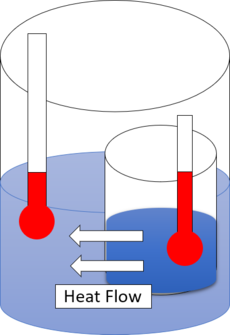
热力学第一定律 First Law Of Thermodynamics定义了热力学系统所涉及到的内能 Internal Energy,[5][6]并体现了能量守恒定律。热力学第二定律与自然过程 Natural Processes的方向有关。它断言自然过程只在一种意义上进行,且不可逆 。例如,当有了传导和辐射的(传播)路径时,热总是自发地从一个较热的物体流向一个较冷的物体。 这种现象可以用[7][8] 熵 Entropy来解释。若一个孤立系统 Isolated System最初在具有隔热内壁的系统内维持热力学平衡,通过一些操作使内壁透热,则该系统可自发地演变,最终达到一个新的内部热力学平衡,且其总熵S增加。
在假想的可逆过程中,系统的熵的无穷小增量[math]\displaystyle{ dS }[/math]被定义为由无穷小的热[math]\displaystyle{ δQ }[/math]传递到一个封闭系统(允许能量进入或出去,但不允许物质传递的系统)除以该平衡系统和提供热的环境的共同温度 [math]\displaystyle{ T }[/math]:[9]
- [math]\displaystyle{ \mathrm dS = \frac{\delta Q}{T} \,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \text {(封闭系统中理想状态下的可逆过程)} }[/math]
用不同的符号δ和d表示无穷小量的热和无穷小量的熵,因为熵是状态函数,而热和功一样,并不是状态函数。对于实际上可能存在的不与环境发生物质交换的无穷小过程,第二定律要求系统熵增量满足不等式: [10][11]
- [math]\displaystyle{ \mathrm dS = \frac{\delta Q}{T} \,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \text {(封闭系统中理想状态下的可逆过程)。} }[/math]
这是因为在这种情况下的一般过程可能包括周围环境对系统所做的功,该功在系统内部会产生摩擦或粘滞效应,此时一个化学反应可能正在系统内部进行,或因为热传递实际上是不可逆地发生,系统温度[math]\displaystyle{ T }[/math]和周围环境温度[math]\displaystyle{ T_surr }[/math]之间的差异驱动了热传递的发生。[12][13] 注意该等式也适用于纯热流 Pure Heat Flow[14]
- [math]\displaystyle{ \mathrm dS = \frac{\delta Q}{T} \,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \text {(实际上可能的,不改变成分的准静态不可逆性)。} }[/math]
这种方法是通过测量热容曲线 Heat Capacity Curves和相变中熵的变化,来准确测定纯物质的绝对熵的基础,[15] [10]比如量热法 calorimetry。
为了描述一个热力学系统在物理平衡状态下(要求有明确定义的等压P和等温T)偏离化学平衡状态,引入一组内部变量[math]\displaystyle{ x_i }[/math],[14] 可以用该等式
- [math]\displaystyle{ \mathrm dS = \frac{\delta Q}{T} - \frac{1}{T} \sum_{j} \, \Xi_{j} \,\delta \xi_j \,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \text {(封闭系统,实际可能的准静态不可逆过程)} }[/math]
第二项代表内部变量的功,这些内部变量可能受到外部影响的干扰,但是系统不能通过内部变量做任何正功。这种说法介绍了热力学系统在时间上演化不可能逆转的性质,并且可以被认为是热力学第二原理的另外一种相当于熵原理的表述。该公式可以被看作使用熵 Entropy的热力学第二定律等价表述[16][17]
热力学第零定律是指如果两个热力学系统都与第三个热力学系统处于热平衡(温度相同)状态,则它们彼此也必定处于热平衡状态。热力学第零定律在它这个简短叙述中让人们认识到热平衡关系中的两个物体具有相同的温度,特别是当一个被测物体与一个参考测温物体具有相同的温度时,[18]对于两个处于热平衡状态的物体,有无限多的经验温标 empirical temperature scales,这通常取决于特定参考温度体的性质。热力学第二定律允许区分温度标度 temperature scale,它定义了一个绝对的热力学温度,与任何特定的参考温度体的性质无关。[19][20]
热力学第二定律的不同表述 Various statements of the law
热力学第二定律可以用许多特定的方式来表达,[21] 最突出的经典陈述是 克劳修斯 Rudolf Clausius (1854)表述,开尔文 克劳修斯 Kelvin Clausius (1851)表述,以及康斯坦丁·卡拉西奥多里 Constantin Carathéodory(1909)在公理化热力学 axiomatic thermodynamics中的表述。这些表述用一般的物理术语来描述定律,引用某些过程的不可能性。克劳修斯和开尔文表述被证明是等价的。
卡诺原理 Carnot's principle
热力学第二定律的历史起源[22]是卡诺原理 Carnot's principle。它指的是卡诺热机 Carnot heat engine的一个循环,卡诺热机以准静态 quasi-static的极限慢速运转,因此热和功在子系统之间进行传递,子系统总是处于它们自己内部的热力学平衡状态。卡诺热机是研究热机效率的工程师特别感兴趣的理想装置。当卡诺发现卡诺原理时,热量理论 caloric theory of heat还没有得到重视,热力学第一定律还没有得到承认,熵的概念还没有数学表达。根据第一定律的解释,它在物理上等同于热力学第二定律,并沿用至今。在热力学第一定律被发现之前,卡诺最初的论点是从热量理论的观点出发的。 下面是他书中的一些例子:
- "...wherever there exists a difference of temperature, motive power can be produced.[23]"
- ...只要有温差,就能产生动力。
- "The production of motive power is then due in steam engines not to an actual consumption of caloric, but to its transportation from a warm body to a cold body ...[24]"
- 动力的产生不是由于蒸汽机实际消耗的热量,而是由于它从一个较热的物体转移到一个较冷的物体...
- "The motive power of heat is independent of the agents employed to realize it; its quantity is fixed solely by the temperatures of the bodies between which is effected, finally, the transfer of caloric.[25]"
- 热的原动力与实现热的媒介无关,热的量完全取决于两个物体之间的温度,最后是热量的传递。[26]
用现代术语,卡诺原理可能更为准确:
- "The efficiency of a quasi-static or reversible Carnot cycle depends only on the temperatures of the two heat reservoirs, and is the same, whatever the working substance. A Carnot engine operated in this way is the most efficient possible heat engine using those two temperatures."
- 准静态卡诺循环或可逆卡诺循环的效率只取决于两种热源的温度,而且无论工作物质是什么,效率是相同的。使用两个热源与工作物质交换热源(一个高温热源温度[math]\displaystyle{ T_1 }[/math]和一个低温热源温度[math]\displaystyle{ T_2 }[/math])的卡诺热机是最有效的热机。[27][28][29][30][31][32]"
克劳修斯表述 Clausius statement
1850年,德国科学家鲁道夫·克劳修斯 Rudolf Clausius 通过研究热传递和功之间的关系,为热力学第二定律奠定了基础。他在1854年用德语发表的论文中所提及的热力学第二定律定义被称为克劳修斯表述:
不可能把热从低温物体传递到高温物体而不产生其他影响。
克劳修斯的表述使用了“热通道 Passage Of Heat”的概念。在热力学的讨论中,通常这意味着“能量作为热的形式的净转移” ,而不是指其他方式的转移。如果不对系统外部做功,热就不能自发地从冷区流向热区,这一点从制冷的普通经验中也可以看出。在冰箱中,只有在外部媒介也就是制冷系统的强制作用下热才会从冷区流到热区。
开尔文表述 Kelvin statements
Lord Kelvin expressed the second law in several wordings.
开尔文勋爵 Lord Kelvin 表述了热力学第二定律。不可能从单一热源取热使之完全转换为有用的功而不产生其他影响。不可能通过无生命物质的作用,将物质的任何部分冷却到低于周围物体最低的温度并产生机械效应 Mechanical Effect。
克劳修斯和开尔文表述的等价性 Equivalence of the Clausius and the Kelvin statements
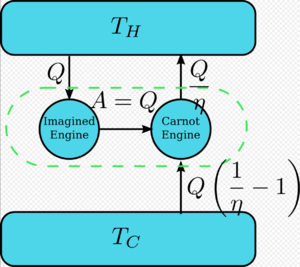
假设有一个热机违反了开尔文定理: 也就是说,这个热机以循环的方式吸收热并将其完全转化为功,而且不产生任何影响。现在将其与反向卡诺机相比较,如图所示。
普通热机的效率为η,反向热机的效率为1/η。这对联合热机的净效应和唯一效应是[math]\displaystyle{ \Delta Q=Q\left(\frac{1}{\eta}-1\right) }[/math] 将热从较冷热源转移到较热热源,这违反了克劳修斯表述。(这是能量守恒定律的结果,因为系统的总能量保持不变[math]\displaystyle{ \text{Input}+\text{Output}=0 \implies Q-\frac{Q}{\eta} = -Q_c }[/math],所以[math]\displaystyle{ Q_c=Q\left( \frac{1}{\eta}-1\right) }[/math]。)因此,违反开尔文表述意味着违反克劳修斯表述,即克劳修斯表述暗示了开尔文表述。我们可以用类似的方式证明开尔文表述暗示了克劳修斯表述,因此两者是等价的。
普朗克命题 Planck's proposition
普朗克 Planck提出了直接来自经验的如下命题。这有时被认为是他对热力学第二定律的表述,但他认为这是热力学第二定律推导的起点。
- "It is impossible to construct an engine which will work in a complete cycle, and produce no effect except the raising of a weight and cooling of a heat reservoir.[33][34]"
- "不可能建造一台发动机,使其在一个完整的循环中工作,并且除了提高重量和冷却热储以外不会产生任何效果。[35][36]
开尔文表述与普朗克命题的关系 Relation between Kelvin's statement and Planck's proposition
教科书中几乎总是用“开尔文-普朗克表述 Kelvin-Planck Statement”来称呼该定律,例如德克·特哈尔 Diek ter Haar 和哈拉尔德·沃格兰 Harald Wergeland 就是这样表述的。[37]热力学第二定律的开尔文-普朗克表述(或称“热机表述 Heat Engine Statement”)指出:
- "It is impossible to devise a cyclically operating device, the sole effect of which is to absorb energy in the form of heat from a single thermal reservoir and to deliver an equivalent amount of work.[38]"
- 设计一种唯一效果是从单一热源吸收热并提供等量的功的循环运行装置是不可能的。[38]
普朗克表述 Planck's statement
普朗克表述第二定律如下:
- "Every process occurring in nature proceeds in the sense in which the sum of the entropies of all bodies taking part in the process is increased. In the limit, i.e. for reversible processes, the sum of the entropies remains unchanged.[39][40][41]"
与普朗克表述非常相似的是乌伦贝克 Uhlenbeck和福特 Ford关于不可逆现象的表述。
- "... in an irreversible or spontaneous change from one equilibrium state to another (as for example the equalization of temperature of two bodies A and B, when brought in contact) the entropy always increases.[42]"
- …在从一个平衡态到另一个平衡态的不可逆或自发的变化中(例如,当两个物体 A 和 B 接触时的温度平衡过程),熵总是增加。[43]
卡拉西奥多里原理 Principle of Carathéodory
康斯坦丁·卡拉西奥多里 Constantin Carathéodory在纯数学公理的基础上进行了热力学公理化 formulated阐明。他对第二定律的陈述被称为卡拉西奥多里原理 Principle of Carathéodory,可以这样表述:[44]
- In every neighborhood of any state S of an adiabatically enclosed system there are states inaccessible from S.
- 在绝热封闭系统的任意状态 S 附近,总有从 S 出发不可达的状态。[45]
通过这个阐明,他首次描述了绝热可达性 Adiabatic Accessibility的概念,并为经典热力学的一个新的子领域,即通常所说的几何热力学 Geometrical Thermodynamics奠定了基础。由卡拉西奥多里原理可以推出,作为热的能量的准静态转移是一个 完整的过程函数 holonomic process function即[math]\displaystyle{ \delta Q=TdS }[/math]。[46]
尽管在教科书几乎惯称卡拉西奥多里原理也是第二定律的一种表述,并认为其与克劳修斯表述或开尔文-普朗克表述等价,但事实并非如此。为了得到第二定律的所有内容,需要对卡拉西奥多里原理补充普朗克表述,即等量功总是增加一个最初处于自身内部热力学平衡的封闭系统的内部能量。[13][47][48]
普朗克原理 Planck's principle
1926年,马克斯·普朗克 Max Planck写了一篇关于热力学基础的重要论文。[47][49] 他指出了以下原理
- "The internal energy of a closed system is increased by an adiabatic process, throughout the duration of which, the volume of the system remains constant.[13]模板:Sfnp"
- 一个封闭系统的内部能量因绝热过程增加,在整个过程中,系统的体积保持不变。[13]
这个公式没有提到热,没有提到温度,甚至没有提到熵,也不一定隐含地依赖于这些概念,但它暗示了第二定律的内容。一个密切相关的表述为,“摩擦力从来不做正功。”[50]普朗克写道: “摩擦生热是不可逆的。”[51][52]
这个普朗克定理没有提到熵,是用物理术语来表述的。它与上面给出的开尔文表述密切相关。[53]相关的是,对于恒定体积和摩尔数的系统,熵是内能的单调函数。然而,普朗克的这个原理实际上并不是普朗克对第二定律的首选表述(见前面小节),而是依赖于熵的概念。
Borgnakke 和 Sonntag 提出的以下表述在某种意义上是对普朗克原理的补充。他们没有将其作为第二定律的完整表述:
- "... there is only one way in which the entropy of a [closed] system can be decreased, and that is to transfer heat from the system.[54]"
- …只有一种方法可以减少(封闭)系统的熵,将热从系统中转移出去。[55]"
与普朗克之前提出的原理不同,这一原理明确地用熵的变化来表示。从系统中去除物质也可以减少系统的熵。
一个其内能有已知表达式(其扩展状态变量的函数)的系统的表述 Statement for a system that has a known expression of its internal energy as a function of its extensive state variables
写成广泛性质(质量,体积,熵……)的函数时,第二定律等价于弱凸函数内能 U。[56][57]
推论
第二类永动机 Perpetual motion of the second kind
卡诺定理 Carnot's Theorem(1824)是一条限制任何可能的热机的最大效率的原理。效率完全取决于热源中热和冷之间的温差。 卡诺定理指出:
- "All irreversible heat engines between two heat reservoirs are less efficient than a Carnot engine"
- 两个储热器之间的所有不可逆热机的效率都低于卡诺发动机
- "All reversible heat engines between two heat reservoirs are equally efficient with a Carnot engine operating between the same reservoirs."
- 两个储热器之间的所有可逆热机均具有相同的效率,而卡诺发动机则在相同的储热器之间运行。
在他的理想模型中,热转化为功的过程可以通过逆转循环的运动而恢复,这个概念后来被称为热力学可逆性 Thermodynamic Reversibility。然而,卡诺进一步假定,一些热量损失了,并没有转化为机械功。因此,没有一个真实的热机能够实现卡诺循环 Carnot Cycle的可逆性,并且被认为效率较低。
该理论尽管是用热量表述的(见被取代的热质说),而不是熵,但是它是对第二定律的早期认识。
克劳修斯不等式 Clausius inequality
克劳修斯定理 Clausius Theorem(1854)指出,在一个循环的过程中
- [math]\displaystyle{ \oint \frac{\delta Q}{T} \leq 0. }[/math]
等号在可逆情况下成立,[58]严格不等号在不可逆情况下成立。可逆情况下引入状态函数熵。这是因为在循环过程中,状态功能的变化相对于状态功能为零。
热力学温度 Thermodynamic temperature
对于任意热机,效率为:
- [math]\displaystyle{ \eta = \frac {W_n}{q_H} = \frac{q_H-q_C}{q_H} = 1 - \frac{q_C}{q_H} \qquad (1) }[/math]
其中 Wn 表示每个循环所做的净功。因此效率只取决于 qC/qH。
卡诺定理指出,所有在相同热源间运行的可逆热机的效率是相同的。
因此,任何在温度T1和T2之间运行的可逆热机必须具有相同的效率,也就是说,效率只是温度的函数:
- [math]\displaystyle{ \frac {q_C}{q_H} = f(T_H,T_C)\qquad (2). }[/math]
另外,在温度 T1 和 T3 之间工作的可逆热机必须具有与由分别在温度T1 和(中间)温度 T2之间、在 T2 和 T3 之间的两个循环组成的系统效率相同。只有下式成立才会出现这种情况:
- [math]\displaystyle{ f(T_1,T_3) = \frac{q_3}{q_1} = \frac{q_2 q_3} {q_1 q_2} = f(T_1,T_2)f(T_2,T_3). }[/math]
现在考虑如下情形,[math]\displaystyle{ T_1 }[/math] 是一个固定的参考温度:水的三相点 Triple Point的温度。则对于任意 T2 和 T3,
- [math]\displaystyle{ f(T_2,T_3) = \frac{f(T_1,T_3)}{f(T_1,T_2)} = \frac{273.16 \cdot f(T_1,T_3)}{273.16 \cdot f(T_1,T_2)}. }[/math]
因此,如果热力学温度被定义为:
- [math]\displaystyle{ T = 273.16 \cdot f(T_1,T) \, }[/math]
那么函数 f 作为热力学温度的函数,为:
- [math]\displaystyle{ f(T_2,T_3) = \frac{T_3}{T_2}, }[/math]
参考温度 T1 的值为273.16。(任何参考温度和任何正值均可用——此处的选择对应开尔文标度。)
熵 Entropy
根据克劳修斯等式,对可逆过程有
- [math]\displaystyle{ \oint \frac{\delta Q}{T}=0 }[/math]
这意味着线积分 [math]\displaystyle{ \int_L \frac{\delta Q}{T} }[/math] 对于可逆过程是路径无关的。所以我们可以定义一个叫做熵的状态函数 S,对于可逆过程或者纯热传递满足:
- [math]\displaystyle{ dS = \frac{\delta Q}{T} \! }[/math]
据此,只有对上述公式进行积分,才能得到熵的差值。为了获得绝对值,我们需要热力学第三定律 Third Law of Thermodynamics,它指出绝对零度 Absolute Zero下完美晶体的 S = 0。对于任意不可逆过程,由于熵是一个状态函数,我们总是可以将初始状态和最终状态与一个虚拟的可逆过程联系起来,并在这条路径上积分以计算熵的差值。
现在把可逆过程逆过来,将其与上述不可逆过程结合。把克劳修斯不等式应用到这个循环,
- [math]\displaystyle{ -\Delta S+\int\frac{\delta Q}{T}=\oint\frac{\delta Q}{T}\lt 0 }[/math]
故,
- [math]\displaystyle{ \Delta S \ge \int \frac{\delta Q}{T} \,\! }[/math]
如果变换可逆,等号成立。注意,若该过程是一个绝热过程 Adiabatic Process,则[math]\displaystyle{ \delta Q=0 }[/math],故[math]\displaystyle{ \Delta S\ge 0 }[/math]。
能量,可用的有用工作 Energy, available useful work
考虑将第二定律应用于孤立系统(称为整体系统或宇宙)是一个重要而具有启发性的理想情形。该系统由两部分组成:研究关心的子系统和子系统的周围环境。因为想象的环境非常大,以至于它们可以被视为一个温度为 TR 且压力为 PR 的无限热源,因此无论有多少热被转移到(或来自)子系统,周围的温度将保持TR ;无论子系统的体积膨胀(或收缩)有多大,周围环境的压力都将保持不变。
无论子系统和周围环境单独地发生什么熵的变化 dS和dSR,根据第二定律,孤立总体系统的熵Stot不能减小。
- [math]\displaystyle{ dS_{\mathrm{tot}}= dS + dS_R \ge 0 }[/math]
根据热力学第一定律,子系统内能的变化 dU 是加在子系统上的热δq 的和,减去子系统所做的任何功w,再加上进入子系统的任何净化学能d ∑μiRNi,因此
- [math]\displaystyle{ dU = \delta q - \delta w + d(\sum \mu_{iR}N_i) \, }[/math]
其中μiR是外部环境中化学形态 chemical species的化学势。
现在热量离开热源进入子系统是:
- [math]\displaystyle{ \delta q = T_R (-dS_R) \le T_R dS }[/math]
在这个过程中,首先使用了经典热力学中熵的定义(在统计热力学中,熵变、温度和吸收热量之间的关系可以将其推导出来) ,然后从上面的公式可以推导出第二定律的不等式。
因此,子系统所做的任何净功δw必须服从
- [math]\displaystyle{ \delta w \le - dU + T_R dS + \sum \mu_{iR} dN_i \, }[/math]
将子系统所做的功δw划分为子系统可以完成的有用功δwu ,除了子系统在周围外部压力下膨胀所做的功pR dV外,给出以下可用功(有效能 exergy)关系式:
- [math]\displaystyle{ \delta w_u \le -d (U - T_R S + p_R V - \sum \mu_{iR} N_i )\, }[/math]
将右侧定义为热力学势的精确导数(称为子系统的有效能或㶲E)很方便,
- [math]\displaystyle{ E = U - T_R S + p_R V - \sum \mu_{iR} N_i }[/math]
因此,第二定律意味着对于任何可以简单地分为子系统和与之接触的温度和压力容器的过程,
- [math]\displaystyle{ dE + \delta w_u \le 0 \, }[/math]
即子系统有用能的变化加上子系统所做的有用功(或者,子系统有用能的变化减去除了压力热源外任何对系统做的功)必须小于或等于零。
总之,如果选择一个合适的类似于无限库的参考状态作为现实世界中的系统环境,则第二定律预测不可逆过程的E值减少,可逆过程的E值不变。
- [math]\displaystyle{ dS_{tot} \ge 0 }[/math] 等价于 [math]\displaystyle{ dE + \delta w_u \le 0 }[/math]
这个表达式和相关的参考状态允许设计工程师在宏观尺度(高于热力学极限)下使用第二定律,而无需直接测量或考虑整个孤立系统中的熵变。这些变化已经在假设中被考虑到,该假设认为所考虑的系统可以在不改变参考状态的情况下与参考状态达到平衡。将其与可逆理想状态进行比较,还可以找到一个过程或过程集合的效率。
第二定律的这种方法被广泛应用于工程实践 engineering practice、环境会计environmental accounting、系统生态学 systems ecology等其他学科。
化学热力学的第二定律 second law in chemical thermodynamics
对于一个恒温恒压封闭系统中的自发化学过程,在没有 non-PV 功的情况下,克劳修斯不等式ΔS > Q/Tsurr由于吉布斯自由能 Gibbs free energy的变化而转化为:
- [math]\displaystyle{ \Delta G \lt 0 }[/math]
或者 dG < 0。对于一个相似的恒温恒压过程,亥姆霍兹自由能 Helmholtz free energy 的变化一定是负的, [math]\displaystyle{ \Delta A \lt 0 }[/math]。因此,一个负的自由能(G 或 A)变化是过程自发的必要条件。这是热力学第二定律在化学中最有用的形式,其中自由能的变化可以通过表列生成焓 Tabulated Enthalpies of Formation和反应物及产物的标准摩尔熵来计算。[10] 在温度和压力不变的情况下,化学平衡条件是 dG = 0。
历史
卡诺 Carnot在1824年提出热转化为机械功的第一个理论。他是第一个正确认识到了转换效率取决于发动机和环境之间的温差的人。
克劳修斯 Rudolf Clausius认识到焦耳 James Prescott Joule在能量守恒方面工作的重要性后,在1850年提出了第二定律的第一个公式,在这个公式中: 热不会自发地从冷物体流向热物体。虽然现在这是常识,但是这与当时流行的热理论相反,当时的热理论认为热是一种流体。从这些他推断出了萨迪卡诺定律 the principle of Sadi Carnot和熵的定义(1865年)。
19世纪提出的开尔文-普朗克第二陈述 Kelvin-Planck 表示:“任何循环运行的设备都不可能从单个热源接收热并产生净功。”这被证明与克劳修斯的陈述等价。
遍历假设 ergodic hypothesis对玻尔兹曼方法 Boltzmann approach也很重要。遍历假设认为在很长一段时间内,在具有相同能量的微观态相空间的某些区域所花费的时间与这个区域的体积成正比,即在很长一段时间内,所有可访问的微观状态出现/成立的可能性都是一样的。等价于说,它表明时间平均值和统计集合的平均值是相同的。
Clausius还提出了一种传统的学说,他认为熵可以被理解为宏观系统中的分子“无序”molecular 'disorder' ,但这种学说已经过时了。[59][60][61]
克劳修斯的描述
1856年,德国物理学家鲁道夫·克劳修斯 Rudolf Clausius阐述了他所谓的“热力学理论中的第二个基本定理 second fundamental theorem in the mechanical theory of heat” ,其形式如下:
- [math]\displaystyle{ \int \frac{\delta Q}{T} = -N }[/math]
其中Q 是热,T 是温度,N 是一个循环过程中所有非补偿的相变的“等价值”。后来在1865年,Clausius将“等价值”定义为熵。基于这个理论,同一年,第二定律最著名的版本在4月24日苏黎世哲学学会的一次演讲中被提出,在演讲的最后Clausius总结道:
- The entropy of the universe tends to a maximum.
- 宇宙的熵趋于最大。
这句话是第二定律最著名的陈述。由于其语言松散模糊,如“宇宙 universe”,和缺乏具体的条件,如“开放 open”,“封闭 closed”,或“孤立 isolated”,许多人认为这一简单的陈述意味着热力学第二定律几乎适用于每一个可以想象的主题。这不是真的;这句话只是一个更广泛和更精确的描述的简化版本。
就时间变化而言,对于经历任意变换的孤立系统,第二定律的数学表述是:
- [math]\displaystyle{ \frac{dS}{dt} \ge 0 }[/math]
这里S 是系统的熵,t是时间。
平衡后用等号。另一种表述孤立系统第二定律的方法是:
- [math]\displaystyle{ \frac{dS}{dt} = \dot S_{i} }[/math] with [math]\displaystyle{ \dot S_{i} \ge 0 }[/math]
用[math]\displaystyle{ \dot S_{i} }[/math]表示系统内所有进程熵产生 Entropy Production的速率之和。这个公式的优点是它显示了熵产生的效果。熵产生率是一个非常重要的概念,因为它决定(或限制)热机的效率。乘以环境温度[math]\displaystyle{ T_{a} }[/math],它给出所谓的耗散能[math]\displaystyle{ P_{diss}=T_{a}\dot S_{i} }[/math]。
封闭系统的第二定律(允许热量交换和边界移动,但不允许物质交换)的表达式是:
- [math]\displaystyle{ \frac{dS}{dt} = \frac{\dot Q}{T}+\dot S_{i} }[/math] with [math]\displaystyle{ \dot S_{i} \ge 0 }[/math]
其中,[math]\displaystyle{ \dot Q }[/math]是进入系统的热流,[math]\displaystyle{ T }[/math] 是热量进入系统时的温度。
只有在系统内发生可逆过程的情况下等号才成立如果发生不可逆过程(在实际操作系统中就是这种情况),则“>”成立。如果系统有多处供热,必须求相应项的代数和。
对于开放系统(允许物质交换) :
- [math]\displaystyle{ \frac{dS}{dt} = \frac{\dot Q}{T}+\dot S+\dot S_{i} }[/math] with [math]\displaystyle{ \dot S_{i} \ge 0 }[/math]
其中,[math]\displaystyle{ \dot S }[/math] 是进入系统的熵流,与进入系统的物质流有关。它不应该与熵的时间导数混淆。如果物质在几个地方被供给,需要取这些贡献的代数和。
统计力学 Statistical mechanics
统计力学通过假设物质是由不断运动的原子和分子组成的,来对第二定律给出了解释。系统中每个粒子的一组特定的位置和速度称为系统的微观状态,由于系统的不断运动,系统不断地改变其微观状态。统计力学假设,在平衡状态下,系统处于每个微观状态的可能性是相等的。这个假设的提出直接导致第二定律必须在统计学意义上成立,也就是说,第二定律在平均意义上成立,其中统计学变异取决于数量级1/[math]\displaystyle{ {\bar{\sqrt{N}}} }[/math] ,其中 N 是系统中粒子数。在日常(宏观)情况下,违反第二定律的概率几乎为零。然而,对于粒子数量很少的系统,热力学参数,包括熵,可能显示出与第二定律预测结果的显著的统计偏差。经典热力学理论不处理这些统计变量。
从统计力学导出 Derivation from statistical mechanics
气体动力学 Kinetic theory of gases理论的第一个力学论证由麦克斯韦 James Clerk Maxwell在1860年给出,指出分子碰撞引起温度均衡化,因此整体趋向于平衡 Equilibrium ; 玻尔兹曼 Ludwig Boltzmann[62]在1872年提出的 H 定理 H-theorem也认为,气体由于碰撞应该随着时间的推移趋向于麦克斯韦-波兹曼分布 Maxwell–Boltzmann distribution。
由于洛施密特悖论 Loschmidt's paradox,第二定律的导出必须对过去做出一个假设,即系统在过去的某个时刻是不相关的;这样的假设允许进行简单的概率处理。这个假设通常被认为是一个边界条件 boundary condition,因此热力学第二定律最终是过去某个地方的初始条件的结果,可能是在宇宙的开始(大爆炸 the Big Bang),尽管也有人提出了其他场景。[63][64][65]
基于这些假设,在统计力学中,第二定律不是一个假设,而是统计力学基本假设 Statistical mechanics#Fundamental postulate|fundamental postulate的一个结果,也被称为等先验概率假设 equal prior probability postulate。这个基本假设表明,只要一个人清楚地知道,简单的概率论证只适用于未来,而对于过去,有辅助的信息来源告诉我们,它是低熵的。如果我们把熵的概念限制在热平衡系统中,那么热力学第二定律的第一部分即热孤立系统的熵只能增加,是等先验概率假设的一个显然结果。处于热平衡状态的孤立系统且具有能量[math]\displaystyle{ E }[/math]的熵表示为:
- [math]\displaystyle{ S = k_{\mathrm B} \ln\left[\Omega\left(E\right)\right]\, }[/math]
其中[math]\displaystyle{ \Omega\left(E\right) }[/math] 是处于 [math]\displaystyle{ E }[/math]和[math]\displaystyle{ E +\delta E }[/math]这个小区间内的量子态数目。这里的 [math]\displaystyle{ \delta E }[/math] 是一个宏观上很小的固定能量区间。严格地说,这意味着熵取决于对[math]\displaystyle{ \delta E }[/math]的选择。然而在热力学极限下(例如无穷大系统的极限),狭义的熵(单位体积或单位质量的熵)不依赖于 [math]\displaystyle{ \delta E }[/math]。
假设我们有一个孤立系统,其宏观状态由许多变量指定。这些宏观变量可以是总体积、活塞在系统中的位置等。从而[math]\displaystyle{ \Omega }[/math]将取决于这些变量的值。如果某个变量不是固定的(我们不会在某个位置夹住活塞) ,那么因为在平衡状态下到达所有可到达状态的可能性是相等的,平衡状态下的自由变量会使 [math]\displaystyle{ \Omega }[/math] 最大,因为这是平衡状态下最可能的情况。
如果该变量最初固定到某个值然后释放,当达到新的平衡时,变量将自我调整使得 [math]\displaystyle{ \Omega }[/math] 最大,这意味着熵将增加或保持不变(如果变量初始固定的值恰好是平衡值)。
假设我们初始位于一个平衡状态,突然移除了对一个变量的约束。我们做完这件事的时候,可达到的微观状态的数为[math]\displaystyle{ \Omega }[/math],但是系统还没有达到平衡,所以系统处于某些可达到的状态的实际概率还不等于先验概率 [math]\displaystyle{ 1/\Omega }[/math]。我们已经知道,最终的平衡状态相对于之前的平衡状态,熵会增加或者保持不变。然而,玻耳兹曼的 H定理 H-theorem证明系统在不处于平衡态的期间,那个量作为时间的函数单调增加。
参考文献
- ↑ http://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node38.html#SECTION05224000000000000000
- ↑ Atkins and de Paula, p.78
- ↑ Zohuri, Bahman (2016). Dimensional Analysis Beyond the Pi Theorem. Springer. p. 111. ISBN 978-3-319-45726-0. https://books.google.com/books?id=pRVuDQAAQBAJ.
- ↑ Jaffe, R.L., Taylor, W. (2018). The Physics of Energy, Cambridge University Press, Cambridge UK, pages 150, 151, 259, 772, 743.
- ↑ Max Planck (1897/1903), pp. 40–41.
- ↑ Munster A. (1970), pp. 8–9, 50–51.
- ↑ Max Planck (1897/1903), pp. 79–107.
- ↑ Bailyn, M. (1994), Section 71, pp. 113–154.
- ↑ Bailyn, M. (1994), p. 120.
- ↑ 10.0 10.1 10.2 Mortimer, R. G. Physical Chemistry. 3rd ed., p. 120, Academic Press, 2008.
- ↑ Fermi, E. Thermodynamics, footnote on p. 48, Dover Publications,1956 (still in print).
- ↑ Adkins, C.J. (1968/1983), p. 75.
- ↑ 13.0 13.1 13.2 13.3 Münster, A. (1970), p. 45.
- ↑ 14.0 14.1 Schmidt-Rohr, K. (2014). "Expansion Work without the External Pressure, and Thermodynamics in Terms of Quasistatic Irreversible Processes" J. Chem. Educ. 91: 402-409. https://dx.doi.org/10.1021/ed3008704
- ↑ Oxtoby, D. W; Gillis, H.P., Laurie Butler(2015).Principles of Modern Chemistry, Brooks Cole. p. 617.
- ↑ Pokrovskii V.N. (2005) Extended thermodynamics in a discrete-system approach, Eur. J. Phys. vol. 26, 769–781.
- ↑ Pokrovskii, Vladimir N. (2013). "A Derivation of the Main Relations of Nonequilibrium Thermodynamics". ISRN Thermodynamics. 2013: 1–9. doi:10.1155/2013/906136.
- ↑ J. S. Dugdale (1996). Entropy and its Physical Meaning. Taylor & Francis. p. 13. ISBN 978-0-7484-0569-5. "This law is the basis of temperature."
- ↑ Mark Zemansky (1968), pp. 207–209.
- ↑ Quinn, T.J. (1983), p. 8.
- ↑ "Concept and Statements of the Second Law". web.mit.edu. Retrieved 2010-10-07.
- ↑ Nicolas Léonard Sadi Carnot (1824/1986).
- ↑ Carnot, S. (1824/1986), p. 51.
- ↑ Carnot, S. (1824/1986), p. 46.
- ↑ Carnot, S. (1824/1986), p. 68.
- ↑ Carnot, S. (1824/1986), p. 68.
- ↑ Clifford Truesdell(1980), Chapter 5.
- ↑ Adkins, C.J. (1968/1983), pp. 56–58.
- ↑ Münster, A. (1970), p. 11.
- ↑ Kondepudi, D., Ilya Prigogine(1998), pp.67–75.
- ↑ Lebon, G., Jou, D., Casas-Vázquez, J. (2008), p. 10.
- ↑ Eu, B.C. (2002), pp. 32–35.
- ↑ Max Planck (1897/1903), p. 86.
- ↑ Roberts, J.K., Miller, A.R. (1928/1960), p. 319.
- ↑ Max Planck (1897/1903),"Treatise on Thermodynamics, translated by A. Ogg, Longmans Green, London, p. 100. p. 86.
- ↑ Roberts, J.K., Miller, A.R. (1928/1960), p. 319.
- ↑ Dirk ter Haar,Harald Wergeland (1966), p. 17.
- ↑ 38.0 38.1 Rao, Y. V. C. (1997). Chemical Engineering Thermodynamics. Universities Press. p. 158. ISBN 978-81-7371-048-3.
- ↑ 39.0 39.1 Max Planck (1897/1903), p. 100.
- ↑ 40.0 40.1 Max Planck (1926), p. 463, translation by Uffink, J. (2003), p. 131.
- ↑ 41.0 41.1 Roberts, J.K., Miller, A.R. (1928/1960), p. 382. This source is partly verbatim from Planck's statement, but does not cite Planck. This source calls the statement the principle of the increase of entropy.
- ↑ George Uhlenbeck, Ford, G.W. (1963), p. 16.
- ↑ George Uhlenbeck|Uhlenbeck, G.E., Ford, G.W. (1963), p. 16.
- ↑ Constantin Carathéodory|Carathéodory, C. (1909).
- ↑ Buchdahl, H.A. (1966), p. 68.
- ↑ Sychev, V. V. (1991). The Differential Equations of Thermodynamics. Taylor & Francis. ISBN 978-1-56032-121-7.
- ↑ 47.0 47.1 Max Planck|Planck, M.(1926).
- ↑ Buchdahl, H.A. (1966), p. 69.
- ↑ Uffink, J. (2003), pp. 129–132.
- ↑ Clifford Truesdell, Muncaster, R.G. (1980). Fundamentals of Maxwell's Kinetic Theory of a Simple Monatomic Gas, Treated as a Branch of Rational Mechanics, Academic Press, New York, p. 15.
- ↑ Max Planck(1897/1903), p. 81.
- ↑ Max Planck (1926), p. 457, Wikipedia editor's translation.
- ↑ Lieb, E.H., Yngvason, J. (2003), p. 149.
- ↑ Borgnakke, C., Sonntag., R.E. (2009), p. 304.
- ↑ Borgnakke, C., Sonntag., R.E. (2009), p. 304.
- ↑ van Gool, W.; Bruggink, J.J.C. (Eds) (1985). Energy and time in the economic and physical sciences. North-Holland. pp. 41–56. ISBN 978-0-444-87748-2.
- ↑ Grubbström, Robert W. (2007). "An Attempt to Introduce Dynamics Into Generalised Exergy Considerations". Applied Energy. 84 (7–8): 701–718. doi:10.1016/j.apenergy.2007.01.003.
- ↑ Clausius theorem at Wolfram Research
- ↑ Denbigh, K.G., Denbigh, J.S. (1985). Entropy in Relation to Incomplete Knowledge, Cambridge University Press, Cambridge UK, pp. 43–44.
- ↑ Grandy, W.T., Jr (2008). Entropy and the Time Evolution of Macroscopic Systems, Oxford University Press, Oxford, pp. 55–58.
- ↑ Entropy Sites — A Guide Content selected by Frank L. Lambert
- ↑ Gyenis, Balazs (2017). "Maxwell and the normal distribution: A colored story of probability, independence, and tendency towards equilibrium". Studies in History and Philosophy of Modern Physics. 57: 53–65. arXiv:1702.01411. Bibcode:2017SHPMP..57...53G. doi:10.1016/j.shpsb.2017.01.001.
- ↑ Hawking, SW (1985). "Arrow of time in cosmology". Phys. Rev. D. 32 (10): 2489–2495. Bibcode:1985PhRvD..32.2489H. doi:10.1103/PhysRevD.32.2489. PMID 9956019.
- ↑ Greene, Brian (2004). The Fabric of the Cosmos. Alfred A. Knopf. p. 171. ISBN 978-0-375-41288-2. https://archive.org/details/fabricofcosmossp00gree.
- ↑ Lebowitz, Joel L. (September 1993). "Boltzmann's Entropy and Time's Arrow" (PDF). Physics Today. 46 (9): 32–38. Bibcode:1993PhT....46i..32L. doi:10.1063/1.881363. Retrieved 2013-02-22.
延申阅读
- Goldstein, Martin, and Inge F., 1993. The Refrigerator and the Universe. Harvard Univ. Press. Chpts. 4–9 contain an introduction to the Second Law, one a bit less technical than this entry.
- Leff, Harvey S., and Rex, Andrew F. (eds.) 2003. Maxwell's Demon 2 : Entropy, classical and quantum information, computing. Bristol UK; Philadelphia PA: Institute of Physics.
- Halliwell, J.J. (1994). Physical Origins of Time Asymmetry. Cambridge. ISBN 978-0-521-56837-1.(technical).
- Carnot, Sadi (1890). Robert Henry Thurston. ed. Reflections on the Motive Power of Heat and on Machines Fitted to Develop That Power. New York: J. Wiley & Sons. (full text of 1897 ed.) (html)
- Stephen Jay Kline (1999). The Low-Down on Entropy and Interpretive Thermodynamics, La Cañada, CA: DCW Industries. .
- Kostic, M (2011). Revisiting The Second Law of Energy Degradation and Entropy Generation: From Sadi Carnot's Ingenious Reasoning to Holistic Generalization. AIP Conference Proceedings. 1411. pp. 327–350. Bibcode 2011AIPC.1411..327K. doi:10.1063/1.3665247. ISBN 978-0-7354-0985-9. also at [1].
外部链接
- Stanford Encyclopedia of Philosophy: "Philosophy of Statistical Mechanics" – by Lawrence Sklar.
- Second law of thermodynamics in the MIT Course Unified Thermodynamics and Propulsion from Prof. Z. S. Spakovszky
- E.T. Jaynes, 1988, "The evolution of Carnot's principle," in G. J. Erickson and C. R. Smith (eds.)Maximum-Entropy and Bayesian Methods in Science and Engineering, Vol 1: p. 267.
- The Second Law of Thermodynamics, BBC Radio 4 discussion with John Gribbin, Peter Atkins & Monica Grady (In Our Time, Dec. 16, 2004)
编者推荐
热力学第二定律与耗散结构
本课程中,将带领大家认识热力学第二定律,重点关注熵是什么,以及它为什么可以构成万事万物演化的时间之箭。
自复制——抵抗热力学第二定律的崭新方法
本课程中,将分析自复制是如何出现,来抵抗热力学第二定律。
自组织理论
本课程中,主要梳理了科学的发展脉络,介绍了时间反演对称、热力学第二定律及自组织现象的理论方法。
本中文词条由Jxzhou、嘉树、趣木木、Jie、沐晨翻译,大白审校,薄荷,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。