玻尔兹曼分布

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
跳到导航 跳到搜索
玻尔兹曼分布是指数分布。
玻尔兹曼因子 pi / pj（纵轴）作为温度 T的函数，用于几个能量差 εi − εj。

在统计力学和数学中，玻尔兹曼分布 Boltzmann distribution（也称为吉布斯分布 Gibbs distribution[1])是一个概率分布或机率量测，它给出了一个系统处于某种量子态的概率，这个概率是该状态的能量和系统温度的函数。分布情况以下列形式表示:

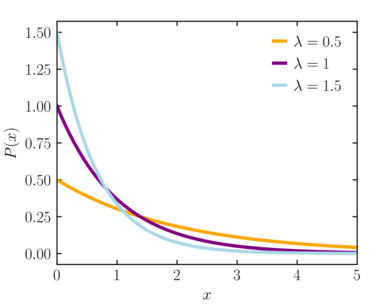
[math]\displaystyle{ p_i \propto e^{-\frac{\varepsilon_i}{kT}} }[/math]


其中，pi 是系统处于状态i的概率, εi 是该状态的能量，还有关于这个分布的一个常数 kT ，它是玻尔兹曼常数k和热力学温度 T 的乘积。符号 [math]\displaystyle{ \propto }[/math]表示正比例(见附录中的比例常数)。


这里的术语系统含义广泛，它可以从单个原子到宏观系统，如天然气储罐。正因为如此，波兹曼分布可以用来解决各种各样的问题。玻尔兹曼分布表明，能量较低的状态被占据的概率总是较高的。


两种状态的概率之比被称为玻尔兹曼因子 Boltzmann factor，取决于两种状态的能量差:

[math]\displaystyle{ \frac{p_i}{p_j} = e^{\frac{\varepsilon_j - \varepsilon_i}{kT}} }[/math]


波兹曼分布是根据路德维希·玻尔兹曼 Ludwig Edward Boltzmann1868年在研究统计力学中气体热平衡的时候首次提出的一个公式命名的。波尔兹曼的统计工作在他1877年的论文《论热力学第二基本定理与热平衡条件的概率计算之间的关系》中得到了体现。[2] 在玻尔兹曼分布被发明之后，约西亚·威拉德·吉布斯 Josiah Willard Gibbs充分地研究了它并在1902年提出了它的一般形式。[3]


广义波兹曼分布是熵的统计力学定义（吉布斯熵公式 [math]\displaystyle{ S = -k_{\mathrm{B}}\sum_i p_i \log p_i }[/math]）与熵的热力学定义（[math]\displaystyle{ d S = \frac{\delta Q_\text{rev}}{T} }[/math]）等价的充要条件。[4]


值得一提的是，玻尔兹曼分布不应与麦克斯韦-玻尔兹曼分布 Maxwell–Boltzmann distribution混淆。前者给出了系统处于某种状态的概率，作为该状态能量的函数；[5] 后者则是用于描述理想气体中的粒子速度。


分布

玻尔兹曼分布是一个概率分布，它给出了出于某种量子态处于某种能量和温度的时候的概率。[6]它被这样定义：

[math]\displaystyle{ p_i=\frac{1}{Q}} {e^{- {\varepsilon}_i / k T}=\frac{e^{- {\varepsilon}_i / k T}}{\sum_{j=1}^{M}{e^{- {\varepsilon}_j / k T}}} }[/math]


其中 pi 是状态 i 的概率，εi 是状态 i 的能量，k 是波兹曼常数，T 是系统的温度，M 是系统所能到达的所有量子态的数目。[5] [6]这里为了简洁美观，省略了kT周围的括弧。归一化的分母Q（被有些作者写为Z）是对于系统中所有量子态进行总和，此部分又被称为正则配分函数 canonical partition function。


所有量子态的概率之和为1.


玻尔兹曼分布是使熵最大化的分布

[math]\displaystyle{ H(p_1,p_2,\cdots,p_M) = -\sum_{i=1}^{M} p_i\log_2 p_i }[/math]


当[math]\displaystyle{ \sum {p_i {\varepsilon}_i} }[/math]等于平均能量值时，玻尔兹曼分布是这种情况下能让熵最大化的分布。我们可以通过拉格朗日乘数法来证明。


在知道量子态能量的情况下，这个配分函数可以被计算。对于原子来说，配分函数的值可以在NIST Atomic Spectra Database中找到。[7]


玻尔兹曼分布指出，能量低的量子态总是有比能量高的量子态更高的概率被粒子占据。它同时也能让我们定量地比较两个量子态分布概率的关系。状态 i 和状态 j 的概率比为

[math]\displaystyle{ {\frac{p_i}{p_j}}=e^{({\varepsilon}_j-{\varepsilon}_i) / k T} }[/math]


其中 pi 是量子态 i 的概率， pj 是量子态 j 的概率，εi 和 εj 分别是状态 i 和 j 的能量。


玻尔兹曼分布通常被用来描述粒子的分布，比如原子或分子，在能量状态上的分布情况。如果我们有一个由许多粒子组成的系统，某个粒子处于量子态 i 的概率就等同于当我们从该系统中选择一个随机的粒子并观察它处于什么状态，发现它处于状态 i 的概率。这个概率等于量子态 i 的粒子数除以系统中粒子的总数，即那些占据量子态i的粒子的比例。

[math]\displaystyle{ p_i={\frac{N_i}{N}} }[/math]


Ni 是位于量子态 i 的粒子数，N是系统中粒子的总数。我们可以用波兹曼分布来求出这个概率，它等于处于量子态i的粒子的比例。所以这个方程给出位于量子态 i 的粒子比例关于这个状态能量的函数[5]。

[math]\displaystyle{ {\frac{N_i}{N}}={\frac{e^{- {\varepsilon}_i / k T}}{\sum_{j=1}^{M}{e^{- {\varepsilon}_j / k T}}}} }[/math]


这个等式对于光谱学来说很重要。在光谱中，我们期待能观察到一条原子或分子跃迁的谱线。[5][8]在为了使这成为可能，必须有一些粒子处于第一个量子态，等待着发生跃迁。我们可以通过求第一态粒子的比例来满足这个条件。如果它可以忽略不计，那么在当前计算的温度下，则很难观察到这种跃迁。一般来说，处于第一状态的分子比例越大，意味着向第二状态跃迁的次数越多。[9]这就产生了一条更强的谱线。然而，还有其他因素影响谱线的强度，例如它是否是被允许的跃迁还是被禁止的跃迁。


玻尔兹曼分布与机器学习中常用的归一化指数函数（Softmax 函数）有关。


统计力学

当独立的（或者几乎独立的）固定体系处于统计力学热平衡状态时，玻尔兹曼分布就会出现。最普遍的情况是概率分布的正则系综，但也有一些特殊的情况（从正则系综衍生）也显示了不同形式的玻尔兹曼分布:

正则系综（一般情况）

正则系综模型给出了在一个封闭固定体积，带有热浴的热平衡系统中的各种可能状态的概率。我们称正则系综为一个玻尔兹曼概率分布。


子系统状态的统计频率（在一个无交互的集合中）

当系统是一个较小子系统的许多非交互副本的集合时，有时我们需要在某个子系统集合中找到某个子系统的统计频率。当应用于这样一个集合时，这个子系统的正则系综具有可分离性: 只要不相互作用的子系统的组成是固定的，那么每个子系统的状态都是独立于其他子系统的，它们也拥有自己的正则系综。因此，子系统状态的期望统计频率分布形式是玻尔兹曼分布。


麦克斯韦-玻尔兹曼统计中的经典气体系统（非相互作用粒子系统）

在粒子系统中，许多粒子共享同一空间，并且相互之间有规律地改变位置; 它们所占据的单粒子状态空间是一个共享空间。麦克斯韦-玻尔兹曼统计给出了在一个给定的单粒子态，在一个处于平衡状态的非相互作用粒子的经典气体中所发现的粒子的预期数量。这个预期的数量分布具有玻尔兹曼分布形式。


虽然这些案例有很多相似之处，但是当关键假设发生变化时，我们需要对它们以不同的方式进行归纳总结，因此区分它们是有帮助的:

  • 当一个系统在能量交换和粒子交换方面都处于热力学平衡时，固定组成的要求就放宽了。这时我们就得到了一个巨正则系综 grand canonical ensemble而不是正则系综。另一方面，如果成分和能量都是固定的，则可以使用微正则系综 microcanonical ensemble。
  • 如果集合中的子系统确实相互交互，则子系统状态的预期频率不再遵循玻尔兹曼分布，甚至可能没有解析解。[10]但是当整个系统是独立的并且处于热平衡状态，则正则系综仍然可以应用于作为一个整体考虑。
  • 对于处于平衡状态的非相互作用粒子的量子气体，在给定的单粒子状态中发现的粒子数量并不遵循麦克斯韦-玻尔兹曼统计。并且正则系综中的量子气体没有简单的封闭表达式。在巨正则系综中，量子气体的统计分布状态由费米-狄拉克统计 Fermi–Dirac statistics或玻色-爱因斯坦统计 Bose–Einstein statistics来描述，具体则取决于该粒子是费米子 fermion还是玻色子 boson。


数学

在更一般的数学环境中，玻尔兹曼分布也被称为吉布斯量度 Gibbs measure。在统计学和机器学习中，它被称为对数线性回归。在深度学习中，玻尔兹曼分布被用于随机神经网络的抽样分布，如玻尔兹曼机 [Boltzmann machine、受限玻尔兹曼机 Restricted Boltzmann machine、基于能量的模型 Energy-Based models和深度波茨曼机 Deep Boltzmann Machine。


经济

在经济学中，玻尔兹曼分布被用来分配排放交易中的许可。[11][12]使用玻尔兹曼分布的新分配方法可以创造出在多个国家之间最可能的、自然的和无偏见的排放许可分配。这种新方法简单而通用，在经济和环保中有很大的应用潜力。


玻尔兹曼分布与多项逻辑回归模型具有相同的形式。在Daniel McFadden登将它与随机效用最大化联系起来之后，成为了大家所熟知的一种离散选择模型。


参考文献

  1. ↑ Landau, Lev Davidovich; Lifshitz, Evgeny Mikhailovich (1980) [1976]. Statistical Physics. Course of Theoretical Physics. 5 (3 ed.). Oxford: Pergamon Press. ISBN 0-7506-3372-7.  Translated by J.B. Sykes and M.J. Kearsley. See section 28
  2. ↑ “On the Relationship between the Second Fundamental Theorem of the Mechanical Theory of Heat and Probability Calculations Regarding the Conditions for Thermal Equilibrium” Sitzungberichte der Kaiserlichen Akademie der Wissenschaften. Mathematisch-Naturwissen Classe. Abt. II, LXXVI 1877, pp 373-435 (Wien. Ber. 1877, 76:373-435).
  3. ↑ Gibbs, Josiah Willard (1902). Elementary Principles in Statistical Mechanics. New York: Charles Scribner's Sons. 
  4. ↑ Gao, Xiang; Gallicchio, Emilio; Roitberg, Adrian (2019). "The generalized Boltzmann distribution is the only distribution in which the Gibbs-Shannon entropy equals the thermodynamic entropy". The Journal of Chemical Physics. 151 (3): 034113. arXiv:1903.02121. doi:10.1063/1.5111333. PMID 31325924.
  5. ↑ 5.0 5.1 5.2 5.3 Atkins, P. W. (2010) Quanta, W. H. Freeman and Company, New York
  6. ↑ 6.0 6.1 McQuarrie, A. (2000) Statistical Mechanics, University Science Books, California
  7. ↑ NIST Atomic Spectra Database Levels Form at nist.gov
  8. ↑ Atkins, P. W.; de Paula J. (2009) Physical Chemistry, 9th edition, Oxford University Press, Oxford, UK
  9. ↑ Skoog, D. A.; Holler, F. J.; Crouch, S. R. (2006) Principles of Instrumental Analysis, Brooks/Cole, Boston, MA
  10. ↑ A classic example of this is magnetic ordering. Systems of non-interacting spins show paramagnetic behaviour that can be understood with a single-particle canonical ensemble (resulting in the Brillouin function). Systems of interacting spins can show much more complex behaviour such as ferromagnetism or antiferromagnetism.
  11. ↑ Park, J.-W., Kim, C. U. and Isard, W. (2012) Permit allocation in emissions trading using the Boltzmann distribution. Physica A 391: 4883–4890
  12. ↑ The Thorny Problem Of Fair Allocation. Technology Review blog. August 17, 2011. Cites and summarizes Park, Kim and Isard (2012).



编者推荐

课程：全同粒子与统计

集智课程

全同粒子与统计

在量子力学中，全同粒子具有不可区分性；粒子体系的哈密顿量具有交换不变性。两个粒子交换位置后，虽然哈密顿量具有不变性，但他们的波函数可以区分出两种情况，即对称波函数和反对称波函数，对应于玻色子和费米子。量子力学中的全同粒子不可分辨，两粒子互换后，与原状态没有区别，不表示新的微观态。微观态计数方法的不同，是经典统计和量子统计的重大区别。

金潮渊老师讲解了光场量子化情形下，光子计数的波动范围遵循一定的统计规律。在可分辨粒子、全同费米子、全同玻色子情况下，微观粒子的三种统计分布，即麦克斯韦-玻尔兹曼统计、玻色-爱因斯坦统计、费米-狄拉克统计。在此基础上，引入狄拉克符号、表象变换、幺正算符等量子力学基本概念和HBT实验即第一个只能用量子理论解释的量子光学实验。


集智文章


本中文词条由tueryeye翻译和审校，薄荷编辑，如有问题，欢迎在讨论页面留言。


本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

取自“https://wiki.swarma.org/index.php?title=玻尔兹曼分布&oldid=33968”