相变
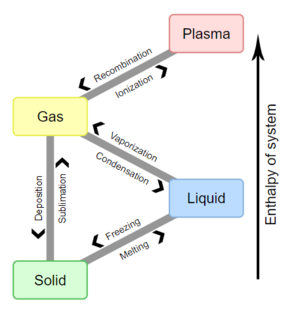
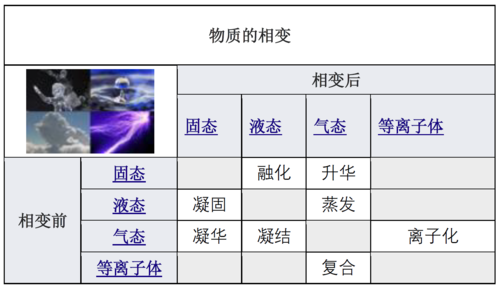
相变Phase transition (or phase change)一词常用于描述物质在固态,液态和气态之间的转变,在极少数情况下还涉及等离子体 plasma 。热力学系统的相位和物质的状态具有统一的物理属性。由于外部条件(例如温度,压强等)的变化,在给定介质的相变过程中介质的某些属性通常会间断的发生变化。例如,液体在被加热到沸点时可能会变成气体,其体积因此发生突变。综合考量变化发生的外部条件,这种变化被称为相变。相变通常发生在自然界,如今被越来越多地用于科技行业。
相变的种类
相变的例子包括:
由于温度和/或压强的影响,单组分在固相,液相和气相之间转换:
- 共晶转变Eutectic transformation,即互溶液体(由两种不同成分组成的单相液体)经过冷却后转变成为两个不同的固相。如果把互溶液体改成固体,那这一过程就被称为共析转变 eutectoid transformation。
- 亚稳态到平衡态的相变。由于较低的表面能而迅速形成的 亚稳多晶体 metastable polymorph,在有足以克服能量位垒的热输入时会逐渐转换为一种平衡相。
- 包晶转变 Peritectic transformation。包含两种不同成分的单相固体经过加热后转变为一种固相和一种液相。
- 亚稳相分解 Spinodal decomposition。一个单相经过冷却后分离为两种不同的相。
- 处于固体和液体过渡状态的 中间相 mesophase,例如一种“液晶 liquid crystal”相。
- 磁性材料处于 居里点 Curie point(居里温度)时,在 铁磁ferromagnetism和 顺磁 paramagnetism相之间转变。
- 在以不同方式组织的 相称 commensurate或 不相称 incommensurate的磁性结构(如在 锑化铈 Antimonide中)之间的转变。
- 马氏体转变 Martensitic transformation,作为碳钢的众多相变之一,也是典型的 位移相变 displacive phase transformations
- 晶体结构 crystallographic structure 的变化,例如铁在 铁素体 Ferrite和 奥氏体 Austenite之间的转变。
- 以α-钛铝化物为例——从有序到无序的转变。
- 以氢对铁(110)的依赖为例¬——吸附几何结构对覆盖率和温度存在依赖性。
- 当冷却到临界温度以下时,某些金属和陶瓷中出现 超导 Superconductivity现象。
- 不同分子结构( 同质多形体 polymorphs, 同素异形体 allotropes或 非晶多形体 polyamorphs)之间的转变——特别是固体之间的,例如非晶结构和晶体结构、两种不同晶体结构之间或两种非晶结构之间。
- 玻色子 Bosonic流体的量子凝聚( 玻色–爱因斯坦凝聚 Bose–Einstein condensation)。液态氦中的超流体转变就是一个例子。
- 物理学中的 对称性破缺 breaking of symmetries——发生在宇宙温度降低的早期阶段
- 同位素分馏Isotope fractionation发生在相变过程中,所涉及分子的轻同位素与重同位素的比率发生变化。当水蒸气冷凝(平衡分馏 equilibrium fractionation )时,较重的同位素(18O和2H)在液相中富集,而较轻的同位素(16O和1H)则趋向于气相。[1]
当系统的热力学自由能无法对某些热力学变量进行解析时,相变就会发生。这通常是因为系统中存在大量相互作用的粒子。如果系统太小,则不会出现。值得注意的是,相变同样可以存在于参数不包括温度的非热力学系统中。例如:量子相变,动态相变和拓扑(结构)相变。在这些系统中,其他参数代替了温度(在 渗滤网络 percolating networks中,连接概率代替温度)。
物质的两个相(液相和气相)在相变点(如沸点)具有相同的自由能,因此它们存在的可能性相同。而当温度低于沸点时,液态在两者中更稳定;当温度高于沸点时,气态更具优势。
有时系统状态可以通过传热方式(与绝热方式相对)改变,这使系统状态得以通过相变点而又不经历相变。此时该系统会处于亚稳态(与发生了相变的相相比,其状态没有那么稳定,但也并非不稳定)。过热、过冷以及过饱和时都会发生这种现象。
分类
埃伦费斯特分类法
保罗·埃伦费斯特Paul Ehrenfest根据热力学自由能和其他热力学变量的函数关系对相变进行了分类[2] 。根据他的方法,可以按照转变时的不连续自由能最低导数标记相变。一阶相变 first-order phase transitions相对于某些热力学变量,具有自由能的一阶导数不连续性。[3] 我们将各种固/液/气的转变都归为一阶相变,因为它们都涉及到密度的不连续变化——这是自由能相对于压力的一阶导数(一阶导数的逆函数)。而 二阶相变 second-order phase transitions在一阶导数中是连续的(有序参量,即自由能相对于外部场的一阶导数,在整个转变过程中是连续的),但在自由能的二阶导数中表现出不连续性。比如铁磁相变ferromagnetic transition (发生在铁等材料中),其中磁化强度是自由能相对于施加磁场强度的一阶导数。随着温度降低到居里温度以下,磁化强度将从零开始持续增加。而磁化率,是自由能相对于磁场的二阶导数,它的变化是不连续的。以此类推,按照Ehrenfest的分类方法,原则上可以存在第三,第四甚至更高阶的相变。
埃伦费斯特分类法 Ehrenfest classification隐含连续相变,其中材料的成键特征发生了变化,但任何自由能导数都没有间断。比如说超临界液气的边界。
现代分类法
在现代分类方案中,相变被分为两大类,命名方式类似于埃伦费斯特分类法:[2]
一阶相变是那些涉及潜伏热的相变。在这种相变过程中,系统会吸收或释放固定(通常是大量)的能量。在此过程中,即使热量增加,系统的温度也保持恒定:系统处于“混合相状态”,也就是说某些部分已完成转变,而其他部分尚未完成。[4][5]常见的例子是冰的融化或水的沸腾(水不会立即变成蒸气,而是成为液态水和蒸气气泡的湍流混合物)。物理学家伊姆利 Imry和沃迪斯 Wortis研究发现,可以将 淬火无序quenched disorder视为一阶转变。即在有限的温度范围内完成相变,但是过冷或过热现象仍然存在,并且滞后仍然存在于热循环中。[6][7][8]
二阶相变或称为“连续相变”,它们的特征是敏感度发散,相关长度无限以及接近临界的相关性幂律衰减。二阶相变的例子是铁磁相变,超导相变superconducting transition (对于I型超导体,在零外场下的相变是二阶的;对于II型超导体,从常态到混合态以及混合态到超导状态的转变都是二阶的)和超流体转换superfluid transition 。另外,对非晶体材料amorphous materials而言,热膨胀thermal expansion和热容属性heat capacity在玻璃相变温度下会发生突变——这与粘度属性相反。[9] 我们可以使用差示扫描量热法来精确检测变化数值。列夫·兰道Lev Landau后来得出了二阶相变的现象学理论。
当改变诸如磁场、成分之类的外部参数时,除了独立、简单的相变,还存在跃迁谱线 transition lines以及多个临界点。
另外还存在其他相变类型,例如无限阶相变 infinite-order phase transitions。无限阶相变是连续的,但并不破坏对称性。最著名的例子是二维XY模型中的KS相变。除此之外, 二维电子气 two-dimensional electron gases 中的量子相变也属于无限阶相变。
在被冷却至远低于结晶相熔点的聚合物和其他液体中出现了液体-玻璃相变 liquid–glass transition。综合考虑多个方面,我们认为这是一种非典型相变。它不是热力学基态之间的转变:因为人们普遍认为,真正的基态始终是晶体。玻璃是淬火无序状态,其熵、密度等取决于热历史。因此,可以把玻璃相变看作一种动态现象:液体冷却时,其内部自由度会逐渐失去平衡。一些理论预测其潜在相变会发生在无限长弛豫时间relaxation times的假设极限内。[10][11] 但是目前并不存在直接的实验证据来支持其存在。
在非平衡条件下,胶体粒子colloidal particles的凝胶化转变被认为是二级相变。[12]
特征属性
相共存
在有限的温度范围内,胶体粒子的凝胶化转变显示为bA紊乱-扩展的一阶转变。随着温度降低,低温平衡相 low-temperature equilibrium phase的分数从零增加到一(100%)。随温度变化而变化的馏分共存创造了许多有趣的可能性。比如在冷却时,一些液体会逐渐玻璃化,而不是转变为平衡晶相equilibrium crystal phase。这种情况往往发生在冷却速率比临界冷却速率快的时候——分子运动变得十分缓慢,以至于分子无法重新排列到晶体位置。[13]分子运动的减速通常发生在气温降至玻璃的形成温度'Tg以下时——这可能需要外部施加压力来实现。[9][14] 如果'Tg落在该一阶冻结相变发生的特定温度范围内,一种有趣的现象就会发生,即当转变不完整时该转变会停止。同理可以考虑在低温下被阻止的一阶磁相变,我们可以观察到不完全的磁相变,即两个磁相同时存在直至到达最低温度。自关于铁磁到反铁磁相变的报道首次公开以来,[15] 人们逐渐发现了各种一阶磁相变的持久相共存现象。包括庞磁电阻锰矿材料colossal-magnetoresistance manganite materials[16][17]、磁制冷材料magnetocaloric materials[18] 、磁性形状记忆材料magnetic shape memory materials[19]等其他材料.[20]当Tg 落在相变发生的温度范围内时,观测结果非常有趣,其一阶磁相变受到了磁场的影响——就像结构相变会受到压力影响一样。不过与压力相比,控制磁场相对容易,这大大提高了研究者们运用穷举法研究Tg 和Tc之间相互作用的成功率。一阶磁相变的相位共存将有助于解决和玻璃有关的一系列突出问题。
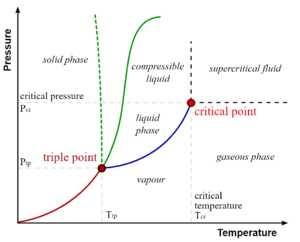
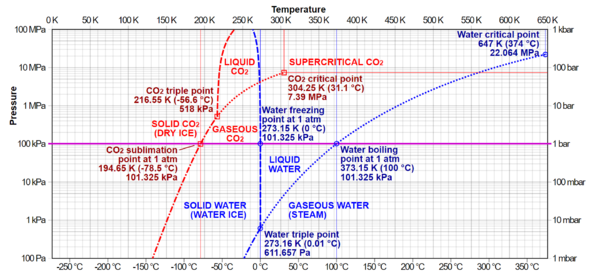
临界点
在任何包含液相和气相的系统中都存在压力和温度的特殊组合,我们称之为临界点。在该临界点处,液相和气相之间的转变即为二级相变。在临界点附近,如果流体足够热并且被压缩,那么液相和气相之间的区别几乎就消失了。这与临界乳光现象有关——液体在所有可能的波长(包括可见光)处产生密度波动,变成乳白色。
对称性
相变通常涉及到对称破坏。例如,将流体冷却至成结晶固体会破坏其连续的平移对称性:流体中的每个点都具有相同的属性,但是晶体中的点并非如此(除非这些点来自晶格点阵中的晶格点)。通常,由于 自发对称性破缺 spontaneous symmetry breaking,除了某些特殊的对称性(例如,重虚粒子 Virtual particles的形成,其仅在低温下发生)外,高温相比低温相具有更多的对称性。[21]
序参量
序参量Order parameter是相变系统中跨边界的有序/无序度量;它通常在一个为零的阶段(通常在临界点以上)和一个非零阶段之间[22] 。在临界点,序参量的敏感性通常会有分离趋向。
序参量的一个示例是发生相变的铁磁系统中的净磁化强度。对于液/气相而言,序参量就是它们的密度之差。
从理论的角度来看,序参量来自对称性破坏。当发生这种情况时,需要引入一个或多个他变量来描述该系统状态。例如,在铁磁相中必须提供净磁化强度,因为当系统降温至居里点以下时,磁化方向会自动确定。但是值得注意的是,非对称性破坏相变也可以定义有序参量。
某些相变,例如 超导 superconducting和铁磁,可以具有超过一个自由度的多个序参量。在这样的相中,序参量可以采用复数、向量 vector甚至张量 tensor的形式,其大小在相变发生时会变为零。
无序参量disorder parameters中存在着相变的双重表述。 这就证明了 线状激励 line-like excitations确实存在,例如 涡旋线 vortex lines, 缺陷线 defect lines等。
宇宙学的相关性
对称性破坏相变在宇宙学中起着重要作用。随着宇宙的膨胀和冷却,太空经历了一系列对称性破坏的相变。例如,电弱过渡破坏了当时电弱场的SU(2)×U(1)对称性,生成了当今电磁场的U(1)对称性。一旦明白宇宙发生过这种转变,对当今宇宙中物质与反物质之间不对称性的研究对我们来说也就更好理解了(请参阅 弱电重子生成 electroweak baryogenesis)。
埃里克·蔡森Eric Chaisson[23] 和戴维·莱泽David Layzer[24]的研究表明,相变正在不断膨胀的宇宙中进行,这与宇宙秩序的发展变化有关。
详情另参见关系秩序理论 relational order theories和秩序与无序。
临界指数和普适性
由于不存在 潜伏热 latent heat,连续相变比一阶相变更容易研究。目前人们已经发现了许多有趣的性质。与连续相变有关的现象由于与临界点有关而被称为临界现象。
事实证明,连续相变可以由临界指数critical exponents这一参数表征。其中最重要的一个参数也许是描述逼近相变时热相关长度差异的指数。例如,让我们检测相变即将发生时的热容行为。在保持其他所有热力学变量不变的条件下,改变系统温度T,发现相变发生在某个临界温度 Tc处。当T接近Tc 时,热容C 通常具有幂律行为':
[math]\displaystyle{ C \propto |T_c - T|^{-\alpha}. }[/math]
当接近玻璃相变温度时,非晶体材料的热容会具有幂律行为,其中通用临界指数α= 0.59[25]。这也适用于相关长度,但要将指数改为ν。
指数ν为正数,这与α不同。临界指数的实际值取决于我们选择的相变类型。
人们曾普遍认为,不管温度在临界温度之上还是临界温度之下,临界指数保持不变。但是现实证明这不一定正确:当连续对称属性因不相关的各向异性anisotropies(在重整化群理论renormalization group意义上)而分解为离散对称属性时,某些指数(例如[math]\displaystyle{ \gamma }[/math], 磁化率指数Exponent of the susceptibility)会有所不同。[26]
当[math]\displaystyle{ -1\lt α\lt 0 }[/math]时,热容在相变温度下具有“扭结”性质。这是液氦liquid helium从正常状态到超流体状态的[math]\displaystyle{ \gamma }[/math]相变行为,在此实验中发现α= -0.013±0.003。为最小化样品中的压力差,至少有一次实验在轨道卫星的零重力条件下进行[27] 。α的这个实验值与基于变分微扰理论variational perturbation theory的预测值相符。[28]
当[math]\displaystyle{ 0\lt α\lt 1 }[/math]时,热容在相变温度处发散(也因为[math]\displaystyle{ α\lt 1 }[/math],所以焓保持有限)。例如3D铁磁相变 3D ferromagnetic phase transition。运用单轴磁体uniaxial magnets的三维伊辛模型three-dimensional Ising model,研究人员通过详细的理论研究得出指数α≈+0.110。
当然,存在一些不遵循幂律行为的模型系统。例如,平均场理论预测了相变温度下热容量的有限不连续性,而二维伊辛模型two-dimensional lsing model则具有对数散度。但是,这样的系统数量有限,是例外。实际上大多相变仍然表现出幂律行为。
另外还存在其他几个临界指数 β, γ, δ, ν和η,主要用于检查相变附近可测物理量的幂律行为。它们通过比例关系相互联系,例如:
[math]\displaystyle{ \beta=\gamma/(\delta-1) , \qquad \nu=\gamma/(2-\eta) }[/math].
上式可以证明只有两个独立的指数,例如 ν和 η。
值得注意的是,在不同系统中发生的相变通常具有相同的临界指数。我们称这种现象为普适性universality。例如,液气临界点的临界指数与流体的化学组成无关。
以上现象很特别,但并非无法理解,它们与单轴磁体中铁磁相变的临界指数完全匹配。人们认为这类系统具有同一普适性。这里的普适性是相变的重整化群理论的一种预测,指出系统在即将相变时的热力学性质仅取决于少数几个特征,例如维数和对称性 ,对系统的基本微观特性并不敏感。同样,相关长度的差异性也是非常重要的因素。
临界慢化和其他现象
在相变过程中,还存在其他临界现象。例如,除了静态函数 static functions外,还存在临界动态。因此在相变发生时,人们可能会观察到明显的减速或加速现象。连续相变的静态普适性可以被分成更小的动态普适性。除了临界指,磁场的某些静态或动态函数以及与临界值的温差也存在普适性关系。
渗流理论
渗流具有临界指数,能够发生相变。最简单的例子是发生在二维方格中的渗流。[29] 其中每一个格子以概率[math]\displaystyle{ p }[/math]标记。对于较小的[math]\displaystyle{ p }[/math]值,格子就形成较小的团簇clusters。但是当[math]\displaystyle{ p }[/math]达到某个阈值pc时就会出现一个巨大的团簇,此时发生二阶相变。pc附近的P∞行为是P∞~(p-pc)β——其中β是一个临界指数。[30][29]
一些其他的领域也可以通过一阶渗流[31]和二阶渗流系统[32] 来定义,人们发现渗流的方法对于研究城市交通和识别可重复性瓶颈非常有用。[33][34]
生物系统中的相变
相变在生物系统中也具有重要的作用。比如 脂质双层 lipid bilayer的形成, 蛋白质折叠 protein folding和 DNA解链 DNA melting过程中的 坍塌转变 coil–globule transition, DNA缩合 DNA condensation过程中的液晶转变,以及具有相变特征的配体与DNA和蛋白质的结合。[35]
在 生物膜 biological membranes中,从凝胶 gel到液晶的相变是其维持生理机能的关键。在凝胶相中,由于膜脂质脂肪酰基链 membrane lipid fatty-acyl chains的流动性低,膜蛋白 membrane proteins的运动受到限制,因此其生理机能的发挥受到限制。植物非常依赖暴露于低温环境下叶绿体类囊体膜 chloroplast thylakoid membranes的光合作用 photosynthesis。由于其高含量的亚麻酸linolenic acid——带有3个双键的18碳链允许高度的脂肪酰基紊乱,[36] 类囊体膜即使在相对较低的温度下也能保持固有的流动性。运用众多技术,包括量热法 calorimetry,荧光法 fluorescence,自旋标记电子顺磁共振 spin label electron paramagnetic resonance和NMR,通过记录各种实验温度下有关参数的测量值来确定生物膜凝胶到液晶相变的温度。人们还提出了一种用13-C NMR谱线强度来测定的简单方法。[37]
曾经有观点认为生物系统可能位于临界点附近。例如蝾螈视网膜中的神经网络[38] bird flocks[39],果蝇中的鸟群基因表达网络和[40] 蛋白质折叠protein folding[41] 。但是,尚不清楚替代原因是否可以解释某些现象来支持关键性论证。[42] 另一个观点认为,生物有机体具有两个重要的相变特性:宏观行为的变化和系统在临界点的一致性。[43]
二阶相变的特征是在某些无标度特性scale-free properties中出现了分形fractals。众所周知,蛋白质球是通过与水的相互作用形成的。蛋白质肽链protein peptide chains上形成侧基的氨基酸amino acids有20种(从亲水性hydrophilic到疏水性hydrophilic都有)使亲水性的氨基酸位于球状表面附近,疏水性的氨基酸更靠近球状中心。实验人员在一个在与溶剂相关的且表面积大于5000个蛋白质片段的区域中发现了二十个分形。[44]这些分形的存在证明了蛋白质在二阶相变的临界点附近起作用。
在处于压力下的生物群中(接近临界转变时),相关性会增强,波动也会增加。许多以人、小鼠、树木和草类植物为研究对象的实验都得出了支持性的结果。[45]
实验性
研究各种效果的方法多种多样。部分示例如下:
- 热重量分析法(非常常见)Thermogravimetry
- X射线衍射法X-ray diffraction
- 中子衍射Neutron diffraction
- 拉曼光谱法Raman Spectroscopy
- SQUID (磁跃迁测量)
- 霍尔效应Hall effect (磁跃迁测量)
- 穆斯堡尔光谱法Mössbauer spectroscopy (同时测量磁性和非磁性跃迁。限制在大约800–1000°C的温度下)
- 扰动角关联Perturbed angular correlation (同时测量磁性和非磁性跃迁。没有温度限制。已经执行了超过2000°C的操作,理论上可能达到最高晶体材料,例如钽碳化carbide 4215°C。)
其他参考资料
- 同素异形体Allotropy
- 自动催化反应和序生成Autocatalytic reactions and order creation
- 晶体生长Crystal growth
- 谷物异常生长Abnormal grain growth
- 差示扫描量热法Differential scanning calorimetry
- 无扩散相变Diffusionless transformations
- 埃伦费斯特方程Ehrenfest equations
- 阻塞(物理)Jamming (physics)
- 开尔文探针力显微镜Kelvin probe force microscope
- 朗道二阶相变理论Landau theory of second order phase transition
- 激光加热基座法Laser-heated pedestal growth
- 物质状态列表List of states of matter
- 微下拉法Micro-pulling-down
- 渗流理论Percolation theory
- 连续介质渗流理论Continuum percolation theory
- 超流体膜Superfluid film
- 超辐射相变Superradiant phase transition
- 拓扑量子场论Topological quantum field theory
参考文献
- ↑ Carol Kendall (2004). "Fundamentals of Stable Isotope Geochemistry". USGS. Retrieved 10 April 2014.
- ↑ 2.0 2.1 Jaeger, Gregg (1 May 1998). "The Ehrenfest Classification of Phase Transitions: Introduction and Evolution". Archive for History of Exact Sciences. 53 (1): 51–81. doi:10.1007/s004070050021.
- ↑ Blundell, Stephen J.; Katherine M. Blundell (2008). Concepts in Thermal Physics. Oxford University Press. ISBN 978-0-19-856770-7.
- ↑ Faghri, A., and Zhang, Y., Transport Phenomena in Multiphase Systems, Elsevier, Burlington, MA, 2006,
- ↑ Faghri, A., and Zhang, Y., Fundamentals of Multiphase Heat Transfer and Flow, Springer, New York, NY, 2020
- ↑ Imry, Y.; Wortis, M. (1979). "Influence of quenched impurities on first-order phase transitions". Phys. Rev. B. 19 (7): 3580–3585. Bibcode:1979PhRvB..19.3580I. doi:10.1103/physrevb.19.3580.
- ↑ Kumar, Kranti; Pramanik, A. K.; Banerjee, A.; Chaddah, P.; Roy, S. B.; Park, S.; Zhang, C. L.; Cheong, S.-W. (2006). "Relating supercooling and glass-like arrest of kinetics for phase separated systems: DopedCeFe2and(La,Pr,Ca)MnO3". Physical Review B. 73 (18): 184435. arXiv:cond-mat/0602627. Bibcode:2006PhRvB..73r4435K. doi:10.1103/PhysRevB.73.184435. ISSN 1098-0121.
- ↑ Pasquini, G.; Daroca, D. Pérez; Chiliotte, C.; Lozano, G. S.; Bekeris, V. (2008). "Ordered, Disordered, and Coexistent Stable Vortex Lattices inNbSe2Single Crystals". Physical Review Letters. 100 (24): 247003. arXiv:0803.0307. Bibcode:2008PhRvL.100x7003P. doi:10.1103/PhysRevLett.100.247003. ISSN 0031-9007. PMID 18643617.
- ↑ 9.0 9.1 Ojovan, M.I. (2013). "Ordering and structural changes at the glass-liquid transition". J. Non-Cryst. Solids. 382: 79–86. Bibcode:2013JNCS..382...79O. doi:10.1016/j.jnoncrysol.2013.10.016.
- ↑ Gotze, Wolfgang. "Complex Dynamics of Glass-Forming Liquids: A Mode-Coupling Theory."
- ↑ Lubchenko, V. Wolynes; Wolynes, Peter G. (2007). "Theory of Structural Glasses and Supercooled Liquids". Annual Review of Physical Chemistry. 58: 235–266. arXiv:cond-mat/0607349. Bibcode:2007ARPC...58..235L. doi:10.1146/annurev.physchem.58.032806.104653. PMID 17067282.
- ↑ Rouwhorst, J; Ness, C.; Soyanov, S.; Zaccone, A.; Schall, P (2020). "Nonequilibrium continuous phase transition in colloidal gelation with short-range attraction". Nature Communications. 11 (1): 3558. arXiv:2007.10691. Bibcode:2020NatCo..11.3558R. doi:10.1038/s41467-020-17353-8. PMC 7367344. PMID 32678089.
- ↑ Greer, A. L. (1995). "Metallic Glasses". Science. 267 (5206): 1947–1953. Bibcode:1995Sci...267.1947G. doi:10.1126/science.267.5206.1947. PMID 17770105.
- ↑ Tarjus, G. (2007). "Materials science: Metal turned to glass". Nature. 448 (7155): 758–759. Bibcode:2007Natur.448..758T. doi:10.1038/448758a. PMID 17700684.
- ↑ Manekar, M. A.; Chaudhary, S.; Chattopadhyay, M. K.; Singh, K. J.; Roy, S. B.; Chaddah, P. (2001). "First-order transition from antiferromagnetism to ferromagnetism inCe(Fe0.96Al0.04)2". Physical Review B. 64 (10): 104416. arXiv:cond-mat/0012472. Bibcode:2001PhRvB..64j4416M. doi:10.1103/PhysRevB.64.104416. ISSN 0163-1829.
- ↑ Banerjee, A.; Pramanik, A. K.; Kumar, Kranti; Chaddah, P. (2006). "Coexisting tunable fractions of glassy and equilibrium long-range-order phases in manganites". Journal of Physics: Condensed Matter. 18 (49): L605. arXiv:cond-mat/0611152. Bibcode:2006JPCM...18L.605B. doi:10.1088/0953-8984/18/49/L02.
{{cite journal}}: Cite has empty unknown parameter:|1=(help) - ↑ Wu W., Israel C., Hur N., Park S., Cheong S. W., de Lozanne A. (2006). "Magnetic imaging of a supercooling glass transition in a weakly disordered ferromagnet". Nature Materials. 5 (11): 881–886. Bibcode:2006NatMa...5..881W. doi:10.1038/nmat1743. PMID 17028576.
{{cite journal}}: CS1 maint: uses authors parameter (link) - ↑ Roy, S. B.; Chattopadhyay, M. K.; Chaddah, P.; Moore, J. D.; Perkins, G. K.; Cohen, L. F.; Gschneidner, K. A.; Pecharsky, V. K. (2006). "Evidence of a magnetic glass state in the magnetocaloric material Gd5Ge4". Physical Review B. 74 (1): 012403. Bibcode:2006PhRvB..74a2403R. doi:10.1103/PhysRevB.74.012403. ISSN 1098-0121.
- ↑ Lakhani, Archana; Banerjee, A.; Chaddah, P.; Chen, X.; Ramanujan, R. V. (2012). "Magnetic glass in shape memory alloy: Ni45Co5Mn38Sn12". Journal of Physics: Condensed Matter. 24 (38): 386004. arXiv:1206.2024. Bibcode:2012JPCM...24L6004L. doi:10.1088/0953-8984/24/38/386004. ISSN 0953-8984. PMID 22927562.
- ↑ Kushwaha, Pallavi; Lakhani, Archana; Rawat, R.; Chaddah, P. (2009). "Low-temperature study of field-induced antiferromagnetic-ferromagnetic transition in Pd-doped Fe-Rh". Physical Review B. 80 (17): 174413. arXiv:0911.4552. Bibcode:2009PhRvB..80q4413K. doi:10.1103/PhysRevB.80.174413. ISSN 1098-0121.
- ↑ Ivancevic, Vladimir G.; Ivancevic, Tijiana, T. (2008). Complex Nonlinearity. Berlin: Springer. pp. 176–177. ISBN 978-3-540-79357-1. https://books.google.com/books?id=wpsPgHgtxEYC&pg=PA177.
- ↑ A. D. McNaught and A. Wilkinson, ed. (1997). Compendium of Chemical Terminology. IUPAC. ISBN 978-0-86542-684-9. http://goldbook.iupac.org/goldbook/O04323.html.
- ↑ Chaisson, Eric J. (2001). Cosmic Evolution. Harvard University Press. ISBN 9780674003422. https://archive.org/details/cosmicevolutionr00chai.
- ↑ David Layzer, Cosmogenesis, The Development of Order in the Universe, Oxford Univ. Press, 1991
- ↑ Ojovan, Michael I.; Lee, William E. (2006). "Topologically disordered systems at the glass transition" (PDF). Journal of Physics: Condensed Matter. 18 (50): 11507–11520. Bibcode:2006JPCM...1811507O. doi:10.1088/0953-8984/18/50/007.
- ↑ Leonard, F.; Delamotte, B. (2015). "Critical exponents can be different on the two sides of a transition". Phys. Rev. Lett. 115 (20): 200601. arXiv:1508.07852. Bibcode:2015PhRvL.115t0601L. doi:10.1103/PhysRevLett.115.200601. PMID 26613426.
- ↑ Lipa, J.; Nissen, J.; Stricker, D.; Swanson, D.; Chui, T. (2003). "Specific heat of liquid helium in zero gravity very near the lambda point". Physical Review B. 68 (17): 174518. arXiv:cond-mat/0310163. Bibcode:2003PhRvB..68q4518L. doi:10.1103/PhysRevB.68.174518.
- ↑ Kleinert, Hagen (1999). "Critical exponents from seven-loop strong-coupling φ4 theory in three dimensions". Physical Review D. 60 (8): 085001. arXiv:hep-th/9812197. Bibcode:1999PhRvD..60h5001K. doi:10.1103/PhysRevD.60.085001.
- ↑ 29.0 29.1 Armin Bunde and Shlomo Havlin (1996). Fractals and Disordered Systems. Springer. http://havlin.biu.ac.il/Shlomo%20Havlin%20books_fds.php.
- ↑ Stauffer, Dietrich; Aharony, Amnon (1994). "Introduction to Percolation Theory". Publ. Math. 6: 290–297. ISBN 978-0-7484-0253-3.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ Bnaya Gross, Hillel Sanhedrai, Louis Shekhtman, Shlomo Havlin (2020). "Interconnections between networks acting like an external field in a first-order percolation transition". Physical Review E. 101 (2): 022316.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ Gaogao Dong, Jingfang Fan, Louis M Shekhtman, Saray Shai, Ruijin Du, Lixin Tian,Xiaosong Chen, H Eugene Stanley, Shlomo Havlin (2018). "Resilience of networks with community structure behaves as if under an external field". Proceedings of the National Academy of Sciences. 115 (25): 6911.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ D. Li, B. Fu, Y. Wang, G. Lu, Y. Berezin, H.E. Stanley, S. Havlin (2015). "Percolation transition in dynamical traffic network with evolving critical bottlenecks". PNAS. 112: 669.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ Guanwen Zeng, Daqing Li, Shengmin Guo, Liang Gao, Ziyou Gao, HEugene Stanley, Shlomo Havlin (2019). "Switch between critical percolation modes in city traffic dynamics". Proceedings of the National Academy of Sciences. 116 (1): 23.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ D.Y. Lando and V.B. Teif (2000). "Long-range interactions between ligands bound to a DNA molecule give rise to adsorption with the character of phase transition of the first kind". J. Biomol. Struct. Dynam. 17 (5): 903–911. doi:10.1080/07391102.2000.10506578. PMID 10798534.
- ↑ YashRoy, R.C. (1987). "13-C NMR studies of lipid fatty acyl chains of chloroplast membranes". Indian Journal of Biochemistry and Biophysics. 24 (6): 177–178.
- ↑ YashRoy, R C (1990). "Determination of membrane lipid phase transition temperature from 13-C NMR intensities". Journal of Biochemical and Biophysical Methods. 20 (4): 353–356. doi:10.1016/0165-022X(90)90097-V. PMID 2365951.
- ↑ Tkacik, Gasper; Mora, Thierry; Marre, Olivier; Amodei, Dario; Berry II, Michael J.; Bialek, William (2014). "Thermodynamics for a network of neurons: Signatures of criticality". arXiv:1407.5946 [q-bio.NC].
- ↑ Bialek, W; Cavagna, A; Giardina, I (2014). "Social interactions dominate speed control in poising natural flocks near criticality". PNAS. 111 (20): 7212–7217. arXiv:1307.5563. Bibcode:2014PNAS..111.7212B. doi:10.1073/pnas.1324045111. PMC 4034227. PMID 24785504.
- ↑ Krotov, D; Dubuis, J O; Gregor, T; Bialek, W (2014). "Morphogenesis at criticality". PNAS. 111 (10): 3683–3688. arXiv:1309.2614. Bibcode:2014PNAS..111.3683K. doi:10.1073/pnas.1324186111. PMC 3956198. PMID 24516161.
- ↑ Mora, Thierry; Bialek, William (2011). "Are biological systems poised at criticality?". Journal of Statistical Physics. 144 (2): 268–302. arXiv:1012.2242. Bibcode:2011JSP...144..268M. doi:10.1007/s10955-011-0229-4.
- ↑ Schwab, David J; Nemenman, Ilya; Mehta, Pankaj (2014). "Zipf's law and criticality in multivariate data without fine-tuning". Physical Review Letters. 113 (6): 068102. arXiv:1310.0448. Bibcode:2014PhRvL.113f8102S. doi:10.1103/PhysRevLett.113.068102. PMC 5142845. PMID 25148352.
- ↑ Longo, G.; Montévil, M. (2011-08-01). "From physics to biology by extending criticality and symmetry breakings". Progress in Biophysics and Molecular Biology. Systems Biology and Cancer. 106 (2): 340–347. arXiv:1103.1833. doi:10.1016/j.pbiomolbio.2011.03.005. PMID 21419157.
- ↑ Moret, Marcelo; Zebende, Gilney (January 2007). "Amino acid hydrophobicity and accessible surface area". Physical Review E. 75 (1): 011920. Bibcode:2007PhRvE..75a1920M. doi:10.1103/PhysRevE.75.011920. PMID 17358197.
- ↑ Gorban, A.N.; Smirnova, E.V.; Tyukina, T.A. (August 2010). "Correlations, risk and crisis: From physiology to finance". Physica A: Statistical Mechanics and Its Applications. 389 (16): 3193–3217. arXiv:0905.0129. Bibcode:2010PhyA..389.3193G. doi:10.1016/j.physa.2010.03.035.
扩展阅读
- Anderson, P.W., 《凝聚态物理的基本概念》, Perseus Publishing (1997).
- Faghri, A., and Zhang, Y., 《多相传热与流动基础》, Springer Nature Switzerland AG, 2020.
- Fisher, M.E. (1974). “临界行为理论中的再规范化”. Rev. Mod. Phys. 46 (4): 597–616. Bibcode:1974RvMP...46..597F. doi:10.1103/revmodphys.46.597.
- Goldenfeld, N., 《关于相变和重整化群的讲座》, Perseus Publishing (1992).
- Ivancevic, Vladimir G; Ivancevic, Tijana T (2008), 《混沌,相变,拓扑变化和路径积分》, Berlin: Springer, ISBN 978-3-540-79356-4, retrieved 14 March 2013
- M.R.Khoshbin-e-Khoshnazar, 《冰的相变作为有限系统相变的一个样本》, (Physics Education(India)Volume 32. No. 2, Apr - Jun 2016)[1]
- Kleinert, H., 《凝聚物质的规范场》, Vol. I, physik.fu-berlin.de “超流体和涡旋线;无序场,相变”, pp. 1–742, World Scientific (Singapore, 1989); Paperback ISBN 9971-5-0210-0 (readable online physik.fu-berlin.de)
- Kleinert, H. and Verena Schulte-Frohlinde, here 《φ4-理论的临界性质》, World Scientific (Singapore, 2001); Paperback ISBN 981-02-4659-5 (readable online here).
- Kogut, J.; Wilson, K (1974). “重整化群和epsilon扩展”. Phys. Rep. 12 (2): 75–199. Bibcode:1974PhR....12...75W. doi:10.1016/0370-1573(74)90023-4.
- Krieger, Martin H., 《物质的构成:对物理现象进行最日常的数学建模》, University of Chicago Press, 1996. 其中包含对Onsager的二维伊辛模型解决方案的详细教学讨论。
- Landau, L.D. and Lifshitz, E.M., 《统计物理学》 Part 1, vol. 5 of Course of Theoretical Physics, Pergamon Press, 3rd Ed. (1994).
- Mussardo G., “统计场论。统计物理学的精确求解模型导论”,Oxford University Press, 2010.
- Schroeder, Manfred R., 《分形,混沌,幂定律:距离无限天堂的分钟路程》, New York: W. H. Freeman, 1991. 写得很好的“半大众”风格的书,而不是教科书,旨在介绍数学和物理科学方面的知识。解释相变的标定是什么。
- H. E. Stanley, 《相变和临界现象导论》(Oxford University Press, Oxford and New York 1971).
- Yeomans J. M., 《相变的统计力学》, Oxford University Press, 1992.
相关链接
- Interactive Phase Transitions on lattices with Java applets 使用Java小程序在晶格上进行交互式相变
- Universality classes 普适性分类 from Sklogwiki
编者推荐
课程推荐
相变与相变模型
本课程由北京师范大学系统科学学院教授吴金闪所讲述,主要讲解了涌现的一种模式“相变”,同时介绍了两种著名的相变模型,即“Ising模型”和“沙堆模型”。
渗流相变
本系列课程为北京师范大学系统科学学院陈晓松老师开设的《复杂性与临界现象》中的渗流相变一节,将介绍不同类型的渗流相变与相对应的临界现象。
本中文词条由Jie编译,和光同尘审校,思无涯咿呀咿呀编辑。欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。