“神经场”的版本间的差异

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
跳到导航 跳到搜索
第134行： 第134行：
  
 
==更多==
 
==更多==
 +
 +
 
[[Propagating Waves]]
 
[[Propagating Waves]]
 
[[Pattern formation]]
 
[[Pattern formation]]
 +
 +
 +
本词条由周昌松老师提供。

2022年6月15日 (三) 16:04的版本

神经场(Neural field)方程是组织层面(tissue-level)的模型，描述了粗粒度(coarsed grained)变量的时空演变(spatiotemporal evolution)，例如神经元群体中的突触(synaptic)或放电率(firing rate)活动。

简介

即使是一小块皮层(cortex)中的神经元和突触的数量也是巨大的。因此，一种流行的建模方法是采用连续极限(continuum limit)并研究神经网络（神经网络中，空间是连续的，并且宏观状态变量(macroscopic state variables)等于平均发放率）。首次尝试开发神经活动的连续近似，或可追溯到 1950 年代的 Beurle (1956)[1] 和 1960 年代的 Griffith (1963, 1965)[2][3]。通过关注给定体积的模型大脑中每单位时间被激活的神经元比例组织，Beurle 能够分析大规模大脑活动的触发和传导。然而，这项工作只处理没有难治(refractory)或恢复变量(recovery variable)的兴奋性(excitatory)神经元网络。Wilson和 Cowan(1972,1973) [4][5]在 1970 年代将 Beurle 的工作扩展到包括抑制性(inhibitory)和兴奋性神经元以及不应期(refractoriness)。Amari (1975, 1977)[6][7] 在对连通性(connectivity)和放电率函数的自然假设下，在对经活动的连续模型中进行了进一步工作，特别是关于模式形成(pattern formation)。Amari 考虑了局部激发(local excitation)和远端抑制(distal inhibition)对于具有典型皮质连接（通常称为“墨西哥帽连接(Mexican hat connectivity)”）的相互作用的抑制性和兴奋性神经元的混合群体，这是一个有效的模型。

由于这些对动态神经场(dynamic neural field)理论的开创性贡献，类似的模型已被用于研究EEG节律(EEG rhythms)、视觉幻觉(visual hallucinations)、短期记忆和运动感知机制。

生理学动机

神经场考虑嵌入在粗粒度空间区域中的神经元群体(Wilson & Cowan 1973)[4]。这种场的颗粒反映了在初级感觉区域(primary sensory areas)中观察到的微观或宏观柱状体，例如啮齿动物的桶状皮层(barrel cortex) (Petersen 2007) [8]或哺乳动物的视觉皮层(visual cortex) (Hubel & Wiesel 1962[9], Saez et al. 1998[10])。此外，神经场考虑瞬时种群放电率(instantaneous population firing rates)（种群编码），即在几毫秒的某个短时间间隔内放电神经元的数量。神经场模型中的时间变量是这个时间间隔的倍数。因此，神经场在时间和空间上是粗粒度的，并表示平均场模型。重要的是要提到与神经质量模型(neural mass models)的相似性，后者忽略了空间扩展，但涉及到关于群体编码(population coding)和时间粒度的相同基本假设。

Beurle(1956)[1]和 Wilson & Cowan(1972, 1973)[5][4]是最早从数学上推导出神经场模型方程的人之一。最近 Faugeras 等人 (2009)[11] 和 Bressloff (2009) [12]考虑到单个神经元的统计特性和随机动力学，给出了不同的推导。有趣的是，他们（Faugeras et al. & Bressloff）[12][11]提出了一个扩展模型，同时考虑了平均活动及其方差的动态，而以前的模型只考虑了平均活动。以下段落给出了神经场模型更具启发性的推导，其中考虑了神经作用的三个主要要素：输入脉冲( incoming pulses)在化学突触处引起的树突电流、受到树突电流(dendritic currents)影响的神经元的放电以及沿轴突(axonal)分支 的动作电位(action potentials)传输。诱发的树突电流 I(t) 服从

[math]\displaystyle{ I(t) = \int_{-\infty}^t {\rm d}\tau^\prime h(t-t^\prime) P(t^\prime)\label{eqn_1} }[/math] (1)

具有化学受体对单个传入脉冲和传入瞬时脉冲序列 P(t) 的突触响应函数 h(t)。 单个突触的实验研究表明某些函数 h(t) 可以很好地近似突触反应行为。 在神经领域，人们考虑一个有效的平均突触响应函数(synaptic response function)，它描述了许多突触对神经群体网络中许多传入脉冲序列的平均响应。 当然，一组突触的平均时间响应可能与单个突触受体的响应函数不同，但形状可能相同。因此，方程(1)也适用于群体树突电流 I(t)，其中涉及有效参数和与突触群体响应函数 h(t)相关的群体放电率 P(t)。

在数学上，从 P(t) 到 I(t) 的转换是具有核(kernel) h(t) 的 Volterra 积分方程。 考虑微分方程通常比考虑积分方程更方便，因此可以尝试计算积分算子(integral operator)的逆(inverse)。 这对于某些积分核函数 h(t) 是可能的。 一个简单且应用广泛的模型是 [math]\displaystyle{ h(t)=\exp(-t/\tau)/\tau }[/math] 衰减时间常数为 [math]\displaystyle{ \tau }[/math]。然后

[math]\displaystyle{ \begin{array}{lcl} \frac{dI(t)}{dt}&=&-\frac{1}{\tau}\int_{-\infty}^t {\rm d}t^\prime \exp\left(-(t-t^\prime)/\tau\right)/\tau P(t^\prime) + \int_{-\infty}^t \left({\rm d}t^\prime/dt\right)|_{\infty}^t \exp\left(-(t-t^\prime)/\tau\right)/\tau P(t^\prime)\\ &=&-\frac{1}{\tau}I(t) + \frac{1}{\tau} P(t) \end{array} }[/math]

应用链式法则和方程(1) 可以写成微分方程

[math]\displaystyle{ \hat{L} I(t)=P(t)\quad,\quad \hat{L}=\tau\frac{d}{dt}+1 . }[/math]

更详细的响应函数及其对应的微分算子(differental operator)是

[math]\displaystyle{ h(t)=\frac{1}{\tau_1-\tau_2}\left(e^{-t/\tau_1}-e^{t/\tau_2}\right) \quad , \quad \hat{L}=\tau_1\tau_2\frac{d^2}{dt^2}+\left(\tau_1+\tau_2\right)\frac{d}{dt}+1 }[/math]

具有较短的上升时间 [math]\displaystyle{ \tau_2 }[/math]和较长的衰减时间 [math]\displaystyle{ \tau_1 }[/math]。 对于 [math]\displaystyle{ \tau_1=\tau_2=\tau }[/math], 响应函数就是所谓的阿尔法函数

[math]\displaystyle{ h(t)=te^{-t/\tau}/\tau\quad , \quad \hat{L}=\tau^2\frac{d^2}{dt^2}+2\tau\frac{d}{dt}+1~. }[/math]

数学框架

在神经组织中电活动传播的许多连续模型中，假设突触输入电流是突触前放电率函数的函数(Wilson & Cowan 1973[4])。 这些无限维动力系统通常是形式上的变体

[math]\displaystyle{ \frac{1}{\alpha} \frac{\partial u(x,t)}{\partial t} = -u + \int_{-\infty}^\infty {\rm d} y w(y) f(u(x-y,t - |y|/v)) . }[/math]

图1 神经场示意图。 这样的模型不仅可以包括轴突延迟的影响，还可以包括突触和树突对放电率信号的过滤。

在这里，u(x,t) 被解释为一个神经场，表示在位置 x 和时间 t 的一组神经元的局部活动。右边的第二项代表突触输入，f 被解释为单个神经元的放电率函数。间隔 y 的神经元之间的连接强度表示为 w(y)，函数 w 通常称为突触足迹(synaptic footprint)。该公式假设系统在空间上是均匀的(homogeneous)和各向同性的(isotropic)。通常 w 反映全局激发 (w>0)、全局抑制 (w<0)、局部激发 - 侧抑制 (墨西哥帽) 描述，例如视觉皮层的方向调整（Somers et al. 1995[13], Ben-Yishai et al. 1995[14]），或反映抑制性中间神经元的短程相互作用和兴奋性锥体细胞的长程相互作用的局部抑制 - 横向激发(local inhibition - lateral excitation)（逆墨西哥帽）。周期性 w 也引起了一些关注（Ben-Yishai et al. 1995[14], Laing and Troy 2003[15]）。参数 [math]\displaystyle{ \alpha }[/math] 是突触的时间衰减率。空间积分下 u 的延迟参数表示由于信号在距离 y 上传播的有限速度引起的轴突传导延迟（Wilson & Cowan 1972[5]；Nunez 1974[16]；Jirsa & Haken 1997[17]）；即 |y|/v 其中 v 是沿轴突纤维的动作电位的速度。最近的扩展涉及轴突传输速度 v 的分布（Atay & Hutt 2006[18]）。

发射率函数有多种自然选择，最简单的是 Heaviside 阶跃函数(step function)。 在这种情况下，神经元最大程度地激发（以绝对不应期设定的速率）或根本不激发，这取决于突触活动是否高于或低于某个阈值。 在制定平均场神经方程的统计力学方法中，这种全有或全无的响应被平滑的 S 形形式所取代（Wilson & Cowan 1972[5]；Amari 1975[6]）。

上面的简单数学模型可以自然地扩展到描述多个群体、皮质层、尖峰频率适应、神经调节、慢离子电流以及更复杂的突触和树突处理形式，如下面的综述文章中所述。

动力学行为

在神经场模型中通常观察到的动态行为类型包括超出图灵不稳定性(Turing instability)的空间和时间周期性模式 (Ermentrout 1979[19]; Tass 1995[20])、局部活动区域，例如颠簸(bumps) (Kishimoto 1979[21]) 和行波(travelling waves) (Ermentrout 1993[22]; Pinto & Ermentrout 2001[23])。在后一种情况下，可以使用(multi-electrode recordings)和成像方法通过实验观察到相应的现象。特别是可以电刺激取自皮层的经过药物处理的组织切片 (Chervin et al. 1988[24]; Golomb & Amitai 1997[25], Wu et al. 1999[26])、海马体 (Miles et al. 1995[27]) 和丘脑 (Kim et al. 1995[28])。 在脑切片中，这些波可以采取癫痫发作期间的同步放电形式(epileptic seizure) (Connors & Amitai 1993[29]) 和与感觉处理相关的传播兴奋 (Ermentrout & Kleinfeld 2001[30])。前额叶皮层的工作记忆（大脑中的信息的临时存储）(Colby et al. 1995[31], Goldman-Rakic 1995[32])，头部方向系统的表征(Zhang 1996[33])，以及视觉皮层的特征选择性，其中颠簸(bumps)的形成与特定神经元反应的调节有关（Ben-Yishai et al. 1995[14]）。

模式形成

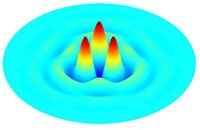
图2 具有短程激发和长程抑制的二维神经场模型中出现超出图灵不稳定性的六边形图案的活动曲线。

神经场模型是非线性空间扩展系统，因此具有支持模式形成的所有必要成分。 这种行为的分析通常结合线性图灵不稳定性理论、弱非线性微扰分析和数值模拟进行。 在一维中，具有墨西哥帽连通性的单一种群模型可以支持全局周期性静止模式(global periodic stationary patterns)。 对于一个以上的人口，非固定（行波）模式也是可能的。 在二维中可能会出现许多其他有趣的模式，例如螺旋波(spiral waves)(Laing 2005[34])、靶向波(target waves)和双周期模式(doubly periodic patterns)。 后面的这些图案采用条纹和棋盘状图案的形式，并且已被 Ermentrout & Cowan (1979)[19] 和 Bressloff et al. (2001) [35]与药物引起的视觉幻觉联系起来。

图3 二维神经场模型中的空间局部化 3-bump 解。

具有短程激发和长程抑制的神经场模型也能够支持空间局部解决方案，通常称为颠簸或多颠簸(multi-bumps)。对于触发率函数是具有阈值 h 的 Heaviside 阶跃函数的情况，Amari (1977) [7]能够构造如下形式的显式单凸点解。

[math]\displaystyle{ u(x) = \int_0^\Delta w(x-y) {\rm d y}, \qquad u(0)=h=u(\Delta) , }[/math]

这样，在某个临界阈值以下，广义和狭义的解并存。在这两者中，更广义的解是稳定的。对于平滑的 sigmoidal 发射率，没有已知的封闭形式的空间局部解，尽管使用最初为研究四阶图案形成系统而开发的技术已经获得了对多颠簸解(multi-bump solutions)形式的深入了解 (Laing & Troy 2003)[36]。静止的活动颠簸(stationary activity bump)可以表现出各种动态不稳定性，包括 Hopf 分岔到空间局部振荡解或呼吸器(breather)(Folias & Bressloff 2004[37]，Coombes & Owen 2004[38])。

活动颠簸(activity bump)的一个可能的计算角色是根据空间结构化网络中颠簸的峰值位置对一组刺激特征进行编码。在同构网络的情况下，允许的特征集将形成反映网络底层拓扑的连续流形(manifold)（吸引子(attractor)）。因此，周期性刺激特征可以由同质环网络中的活动颠簸编码（Ben-Yishai et al. 1995[14]，Zhang 1995[33]）。然而，同质网络的后果之一是，相对于与连续流形相切的空间平移，颠簸将略微稳定。这意味着在存在任意小的噪声水平的情况下，活动颠簸会随着时间缓慢漂移（Laing & Chow 2001[39]）。构建对噪声具有鲁棒性的神经场模型的一种方法是引入某种形式的细胞双稳态（Camperi & Wang 1998[40]，Fall et al. 2004[41]）。

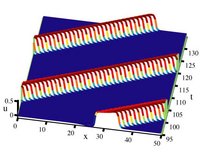
行波

图4 具有尖峰频率自适应的一维神经场模型中的行进脉冲。

对于具有 sigmoid 发射率函数和兴奋耦合的一维模型，可以找到将激发态连接到静止态的波前 (Ermentrout & McLeod 1993[42])。 此外，在具有混合（兴奋性和抑制性）耦合的系统或具有自适应电流的兴奋性系统中，单独的行进脉冲也是可能的。 对于具有阈值 h 的 Heaviside 发射率函数，已经获得了许多关于行波的精确结果。 例如，在 w(x)=exp(-|x|)/2 的纯兴奋性网络中，稳定行进前沿的速度采用显式形式

[math]\displaystyle{ c = \frac{v(2h-1)}{2h-1 - 2 h v/\alpha} }[/math]

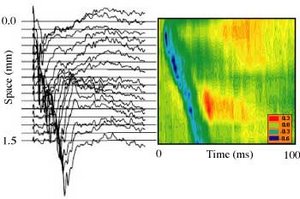
图5 切片实验中传播的电活动波，来自 Pinto Lab (经过允许)。 左：来自 16 个电极的线性阵列的局部场电位记录。 右：该字段的平滑颜色编码版本。

现在，Richardson 等人在真实的神经组织（浸泡在 GABA_A 阻滞剂印防己毒素中的大鼠皮质切片）中间确定了波速对阈值 h 的强烈依赖性(Richardson et al. 2005[43])。 这些实验利用了这样一个事实，即皮质神经元具有长的顶端树突，并且很容易被电场极化，并且癫痫样爆发(epileptiform bursts)可以由刺激电极引发。跨切片施加的正（负）电场增加（降低）波传播速度，这与假设正（负）电场降低（增加）阈值 h 的神经场理论的理论预测一致。

行波的分岔结构(bifurcation structure)可以使用所谓的埃文斯函数(Evans function)来分析。这最初是由 Evans (1975)[44] 在关于霍奇金-赫胥黎(Hodgkin–Huxley)类型的可兴奋神经轴突方程的稳定性定理的背景下制定的。这个复解析函数的零点决定了算子的法线谱，该算子是通过将系统关于其行波解进行线性化而获得的。神经场模型的扩展是最近才出现的，对于 Heaviside 放电率函数的特殊情况，现在已经研究了几个模型（Coombes & Owen 2004, 2005[45][46]）。

大多数神经场模型中的一个常见假设是网络是同质的和各向同性的，也就是说，权重分布取决于网络内互相作用的群体之间的距离。然而，由于在皮层表层中发现的长程水平连接的斑块性质(patchy nature)，真正的皮层更现实地被建模为各向异性和不均匀的二维介质（Bosking et al. 1997[47]）。权重分布的各向异性(Anisotropies)可能导致不同方向的波速变化，而不均匀性(inhomogeneities)可能导致随时间变化的波剖面，并可能导致波传播失败（Bressloff 2001[48]）。

参考文献

  1. ↑ 1.0 1.1 R L Beurle. Properties of a mass of cells capable of regenerating pulses. Philosophical Transactions of the Royal Society London B, 240:55–94, 1956.
  2. ↑ J S Griffith. A field theory of neural nets: II: Properties of field equations. Bulletin of Mathematical Biophysics, 27:187–195, 1965.
  3. ↑ J S Griffith. A field theory of neural nets: I: Derivation of field equations. Bulletin of Mathematical Biophysics, 25:111–120, 1963.
  4. ↑ 4.0 4.1 4.2 4.3 H R Wilson and J D Cowan. A mathematical theory of the functional dynamics of cortical and thalamic nervous tissue. Kybernetik, 13:55–80, 1973.
  5. ↑ 5.0 5.1 5.2 5.3 H R Wilson and J D Cowan. Excitatory and inhibitory interactions in localized populations of model neurons. Biophysical Journal, 12:1–24, 1972.
  6. ↑ 6.0 6.1 S Amari. Homogeneous nets of neuron-like elements. Biological Cybernetics, 17:211–220, 1975.
  7. ↑ 7.0 7.1 S Amari. Dynamics of pattern formation in lateral inhibition type neural fields. Biological Cybernetics, 27:77–87, 1977.
  8. ↑ C C Petersen. The functional organization of the barrel cortex. Neuron 56(2):339-55, 2007.
  9. ↑ D H Hubel and T N Wiesel. Receptive Fields, Binocular Interaction And Functional Architecture In The Cat's Visual Cortex. Journal of Physiology 160:106–154, 1962
  10. ↑ J A Saez, J Paniagua, I Dominguez & J M Ferrer. Image processing in the primary visual cortex. Review Neurology 26(151):439-44, 1998.
  11. ↑ 11.0 11.1 O Faugeras, J Touboul and B Cessac. A constructive mean field analysis of multi population neural networks with random synaptic weights and stochastic inputs. Frontiers of Computational Neuroscience, 3:1, 2009
  12. ↑ 12.0 12.1 P C Bressloff. Stochastic neural field theory and the system-size expansion. SIAM J. Applied Mathematics, 70:1488-1521, 2009
  13. ↑ D C Somers, S B Nelson and M Sur. An emergent model of orientation selectivity in cat visual cortical simple cells. Journal of Neuroscience 15(8), 5448-5465, 1995
  14. ↑ 14.0 14.1 14.2 14.3 R Ben-Yishai, L Bar-Or, and H Sompolinsky. Theory of orientation tuning in visual cortex. Proceedings of the National Academy of Sciences USA, 92:3844–3848, 1995.
  15. ↑ C R Laing and W C Troy. PDE methods for nonlocal models. SIAM Journal on Applied Dynamical Systems, 2:487–516, 2003.
  16. ↑ P L Nunez. The brain wave equation: a model for the EEG. Mathematical Biosciences, 21:279–297, 1974.
  17. ↑ V K Jirsa and H Haken. A derivation of a macroscopic field theory of the brain from the quasi-microscopic neural dynamics. Physica D, 99:503–526, 1997.
  18. ↑ F.M. Atay and A.Hutt, Neural fields with distributed transmission speeds and long-range feedback delays. SIAM Journal Applied Dynamical Systems 5(4), 670-698, 2006
  19. ↑ 19.0 19.1 G B Ermentrout and J D Cowan. A mathematical theory of visual hallucination patterns. Biological Cybernetics, 34:137–150, 1979.
  20. ↑ P Tass. Cortical pattern formation during visual hallucinations. Journal of Biological Physics, 21:177–210, 1995.
  21. ↑ K Kishimoto and S Amari. Existence and stability of local excitations in homogeneous neural fields. Journal of Mathematical Biology, 7:303–318, 1979.
  22. ↑ G B Ermentrout and J B McLeod. Existence and uniqueness of travelling waves for a neural network. Proceedings of the Royal Society of Edinburgh, 123A:461–478, 1993.
  23. ↑ G B Ermentrout and D Kleinfeld. Traveling electrical waves in cortex: Insights from phase dynamics and speculation on a computational role. Neuron, 29:33–44, 2001.
  24. ↑ R D Chervin, P A Pierce, and BWConnors. Periodicity and directionality in the propagation of epileptiform discharges across neortex. Journal of Neurophysiology, 60:1695–1713, 1988.
  25. ↑ D Golomb and Y Amitai. Propagating neuronal discharges in neocortical slices: Computational and experimental study. Journal of Neurophysiology, 78:1199–1211, 1997.
  26. ↑ J Y Wu, L Guan, and Y Tsau. Propagating activation during oscillations and evoked responses in neocortical slices. Journal of Neuroscience, 19:5005–5015, 1999.
  27. ↑ R Miles, R D Traub, and R K S Wong. Spread of synchronous firing in longitudinal slices from the CA3 region of Hippocampus. Journal of Neurophysiology, 60:1481–1496, 1995.
  28. ↑ U Kim, T Bal, and D A McCormick. Spindle waves are propagating synchronized oscillations in the ferret LGNd in vitro. Journal of Neurophysiology, 74:1301–1323, 1995.
  29. ↑ B W Connors and Y Amitai. Generation of epileptiform discharges by local circuits in neocortex. In P A Schwartzkroin, editor, Epilepsy: Models, Mechanisms and Concepts, pages 388–424. Cambridge University Press, 1993.
  30. ↑ G B Ermentrout and D Kleinfeld. Traveling electrical waves in cortex: Insights from phase dynamics and speculation on a computational role. Neuron, 29:33–44, 2001.
  31. ↑ C L Colby, J R Duhamel, and M E Goldberg. Oculocentric spatial representation in parietal cortex. Cerebral Cortex, 5:470–481, 1995.
  32. ↑ P S Goldman-Rakic. Cellular basis of working memory. Neuron, 14:477–485, 1995.
  33. ↑ 33.0 33.1 K Zhang. Representation of spatial orientation by the intrinsic dynamics of the head-direction cell ensemble: a theory. Journal of Neuroscience, 16:2112–2126, 1996.
  34. ↑ C R Laing. Spiral waves in nonlocal equations. SIAM Journal on Applied Dynamical Systems, 4:588-606, 2005.
  35. ↑ P C Bressloff. Traveling fronts and wave propagation failure in an inhomogeneous neural network. Physica D, 155:83-100, 2001.
  36. ↑ C R Laing and W C Troy. PDE methods for nonlocal models. SIAM Journal on Applied Dynamical Systems, 2:487–516, 2003.
  37. ↑ S E Folias and P C Bressloff. Breathing pulses in an excitatory neural network. SIAM J. Appl. Dyn. Syst., 3:378-407, 2004.
  38. ↑ S Coombes and M R Owen. Evans functions for integral neural field equations with Heaviside firing rate function. SIAM Journal on Applied Dynamical Systems, 34:574–600, 2004.
  39. ↑ C R laing and C C Chow. Stationary bumps in networks of spiking neurons. Neural Comput., 13:1473–1494, 2001.
  40. ↑ M Camperi and X-J Wang. A model of visuospatial short-term memory in prefrontal cortex: recurrent network and cellular bistability. J. Comp. Neurosci., 5:383-405, 1998.
  41. ↑ C P Fall, T J Lewis and J Rinzel. Background-activity-dependent properties of a network model for working memory that incorporates cellular bistability. Biological Cybernetics, 93:109-18, 2004.
  42. ↑ G B Ermentrout and J B McLeod. Existence and uniqueness of travelling waves for a neural network. Proceedings of the Royal Society of Edinburgh, 123A:461–478, 1993.
  43. ↑ K A Richardson, S J Schiff, and B J Gluckman. Control of traveling waves in the mammalian cortex. Physical Review Letters, 94:028103, 2005.
  44. ↑ J Evans. Nerve axon equations: IV The stable and unstable impulse. Indiana University Mathematics Journal, 24:1169–1190, 1975.
  45. ↑ S Coombes and M R Owen. Bumps, breathers, and waves in a neural network with spike frequency adaptation, Physical Review Letters, 94, 148102, 2005.
  46. ↑ S Coombes and M R Owen. Evans functions for integral neural field equations with Heaviside firing rate function. SIAM Journal on Applied Dynamical Systems, 34:574–600, 2004.
  47. ↑ W H Bosking, Y Zhang, B Schofield and D Fitzpatrick. Orientation selectivity and the arrangement of horizontal connections in tree shrew striate cortex. J. Neurosci., 17:2112-2127, 1997.
  48. ↑ P C Bressloff. Traveling fronts and wave propagation failure in an inhomogeneous neural network. Physica D, 155:83-100, 2001.

Internal references

  • Yuri A. Kuznetsov (2006) Andronov-Hopf bifurcation. Scholarpedia, 1(10):1858.
  • John W. Milnor (2006) Attractor. Scholarpedia, 1(11):1815.
  • Eugene M. Izhikevich (2006) Bursting. Scholarpedia, 1(3):1300.
  • Philip Holmes and Eric T. Shea-Brown (2006) Stability. Scholarpedia, 1(10):1838.
  • S. Murray Sherman (2006) Thalamus. Scholarpedia, 1(9):1583.


参考 http://www.scholarpedia.org/article/Neural_fields

外部链接

近期综述文章

Preprint available.

Preprint available.

Preprint available.

Preprint available.

Preprint available.

推荐阅读

  • Electric Fields of the Brain: The Neurophysics of EEG, by Paul L. Nunez and Ramesh Srinivasan, Oxford University Press, 2006.

更多

Propagating Waves Pattern formation


本词条由周昌松老师提供。

取自“https://wiki.swarma.org/index.php?title=神经场&oldid=32265”