突变理论
在数学上,突变论是动力学系统研究里分岔理论的一个分支;而在几何学中,它也是奇点理论里的一个特殊情形。
分岔理论对环境中微小变化导致系统动力学行为发生突变的现象进行研究和分类,对动力学方程的解如何依赖方程中的参数进行定性分析。这可能会导致突然而剧烈的变化,例如,无法对时间和规模进行预测的滑坡现象。
突变论起源于20世纪60年代法国数学家托姆 René Thom的一系列工作。得益于Christopher Zeeman的努力,突变论在20世纪70年代变得非常流行。突变论考虑这样一种特殊情况:长期稳定的平衡可以由一个光滑的、定义明确的势函数(李雅普诺夫函数)的最小值确定。
非线性系统某些参数的微小变化可以导致平衡态的出现或消失,或者从吸引变为排斥,又或相反,从而导致系统行为产生巨大而突然的变化。然而,在较大的参数空间中,突变论揭示了这种分叉点往往作为定性几何结构的一部分出现。
基本的灾难
突变论分析势函数的退化临界点(在退化临界点处,势函数不仅一阶导数为零,而且有一个或多个高阶导数也为零),这被视为突变几何的萌芽。临界点的退化可以通过在参数的微小扰动中将势函数按照泰勒级数来展开。
当退化点不只是巧合的,而且是结构性稳定的,退化点作为具有较低退化度的特定几何结构的组织中心存在,其周围的参数空间具有临界特征。如果势函数依赖于两个或更少的活动变量以及四个或更少的活动参数,那么对于这些分支几何形状,只有七个通用结构,具有可以通过微分同胚(一种逆光滑的光滑变换)将灾变芽周围的泰勒级数转化为相应的标准形式。[citation needed]这七种基本类型现在被呈现出来,Thom也给他们取了名字。
一个有效变量的势函数
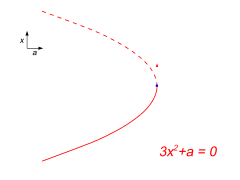
折叠灾难
- [math]\displaystyle{ V = x^3 + ax\, }[/math]
在负值 a 时,势 v 有两个极值,一个是稳定的,一个是不稳定的。如果参数 a 缓慢增加,系统可以达到稳定的最小点。但在0时,稳定极值与不稳定极值相遇并湮灭。这就是分歧点。这儿不再有一个稳定解。如果一个物理系统经过一个折叠分叉,人们就会发现,当 a 到达0时,解的稳定性会突然丧失,系统也会突然转变为一个新的,非常不同的行为。参数 a 的这个分叉值有时被称为“引爆点”。
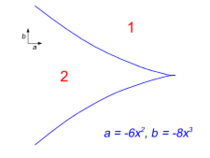
尖点灾变
- [math]\displaystyle{ V = x^4 + ax^2 + bx \, }[/math]
当人们探索如果在控制空间中加入第二个参数 b,将会发生什么,尖点几何是非常常见的。通过改变参数,我们发现在(a,b)空间中存在一条点的曲线(蓝色) ,在这条曲线中解失去了稳定性,其突然跳跃到另一个结果。
但在尖点几何中,分叉曲线回到自身,形成第二个分支,在这个分支中,这个交替解本身失去了稳定性,并将跳回到原来的解集。通过反复增加b,然后减小 b,人们因此可以观察到滞后回路,因为系统交替地遵循一个解决方案,跳到另一个解决方案,沿着另一个解决方案回来,然后跳回到第一个。
然而,这只有在参数空间的区域才可能a < 0。随着a的增加,磁滞回线变得越来越小,直到大于a = 0磁滞回线完全消失(尖点突变) ,只有一个稳定的解。
我们也可以考虑,如果一个人保持b常数,改变a会发生什么。在对称情形b = 0中,我们观察到a被还原时的叉式分岔,当物理系统通过尖点(0,0)时,一个稳定解突然分裂成两个稳定解和一个不稳定解a < 0(自发对称性破缺的一个例子)。离开尖点,所遵循的物理解没有突然的变化: 当通过折叠分叉曲线时,所发生的是一个备用的第二解变得可用。
一个著名的建议是尖点灾难可以用来模拟一只受到压力的狗的行为,它可能会变得胆怯或生气。[1] 建议是,在适度的压力(a > 0) ,狗将展示一个平稳过渡的反应,从吓唬到愤怒,这取决于它是如何挑起的。但是较高的应力水平对应于向该区域的移动(a < 0)。然后,如果狗开始恐吓,它会继续恐吓,因为它被激怒越来越多,直到它达到“折叠”点,其会突然,不间断地跳转到愤怒的模式。一旦进入“愤怒”模式,即使直接刺激参数大大降低,它也会继续愤怒。
一个简单的机械系统,“塞曼灾难机器” ,很好地说明了尖点灾难。在这种装置中,弹簧末端位置的平滑变化可以引起附加轮转动位置的突然变化。[2]
并联冗余复杂系统的灾变失效可以根据局部应力与外部应力之间的关系进行评估。结构断裂力学模型与尖点突变行为相似。该模型预测了复杂系统的储备能力。
其他应用还包括化学和生物系统[3] 中经常遇到的外层电子转移和房地产价格模型。[4]
折叠分岔和尖点几何是迄今为止突变理论最重要的实际结果。它们是在物理学、工程学和数学模型中反复出现的模式。
它们产生强烈的引力透镜效应事件,为天文学家提供了探测黑洞和宇宙暗物质的方法之一——通过引力透镜效应现象产生遥远类星体的多幅图像。[5]
剩下的简单的灾难几何图形在比较中非常专业,在这里展示只是为了好奇的价值。
燕尾蝶灾难
- [math]\displaystyle{ V = x^5 + ax^3 + bx^2 + cx \, }[/math]
控制参数空间为三维空间。参数空间中的分岔集是由三个折叠分岔曲面组成的,这三个折叠分岔曲面在两条尖点分岔线上相交,而尖点又在一个单燕尾分岔点上相交。
当参数经过折叠分叉面时,势函数的一个最小值和一个最大值消失。在尖点分岔处,两个最小值和一个最大值被一个最小值所代替; 在它们之后,折点分岔就消失了。在燕尾点a > 0,两个极小值和两个极大值都在一个x的值上相交。对于燕尾蝶,根据b和c的值,有一个最大-最小对,或者根本没有,这取决于折叠分叉的两个面,以及它们相遇的两条尖形分叉线a < 0,因此在燕尾蝶点消失,只剩下一个单一的折叠分叉面。萨尔瓦多 · 达利的最后一幅画《燕子尾巴》就是以这场灾难为基础的。
蝴蝶灾难
- [math]\displaystyle{ V = x^6 + ax^4 + bx^3 + cx^2 + dx \, }[/math]
根据参数值的不同,势函数可能由折叠分叉的轨迹分开有三个、两个或一个不同的局部极小值。在蝶形点处,折叠分叉的不同三面、尖点分叉的两面、燕尾分叉的线条都相遇并消失,留下一个单一的尖点结构a > 0。
两个活动变量的势函数
脐带灾难是2次灾难的例子。它们可以在光线从三维表面反射而形成的焦面的光学中观察到,并且与近球面的几何形状密切相关。
Thom 提出双曲线脐状突变模拟了波的破裂,椭圆脐状突变模拟了毛发状结构的产生。
双曲线脐点突变
- [math]\displaystyle{ V = x^3 + y^3 + axy + bx +cy \, }[/math]
椭圆脐灾变
- [math]\displaystyle{ V = \frac{x^3}{3} - xy^2 + a(x^2+y^2) + bx + cy \, }[/math]
抛物线脐点突变
- [math]\displaystyle{ V = x^2y + y^4 + ax^2 + by^2 + cx + dy \, }[/math]
阿诺德记数法
弗拉迪米尔 · 阿诺德将这些灾难归为 ADE 类,因为它们与简单的李群有很深的联系。
- A0 - a non-singular point: [math]\displaystyle{ V = x }[/math].
- A1 - a local extremum, either a stable minimum or unstable maximum [math]\displaystyle{ V = \pm x^2 + a x }[/math].
- A2 - the fold
- A3 - the cusp
- A4 - the swallowtail
- A5 - the butterfly
- Ak - a representative of an infinite sequence of one variable forms [math]\displaystyle{ V=x^{k+1}+\cdots }[/math]
- D4− - the elliptical umbilic
- D4+ - the hyperbolic umbilic
- D5 - the parabolic umbilic
- Dk - a representative of an infinite sequence of further umbilic forms
- E6 - the symbolic umbilic [math]\displaystyle{ V = x^3+y^4+a x y^2 +bxy+cx+dy+ey^2 }[/math]
- E7
- E8
在奇点理论中有一些对象,它们对应于大多数其他简单的李群。
参见
- Broken symmetry
- Butterfly effect
- Chaos theory
- Domino effect
- Inflection point
- Morphology (biology)|Morphology
- Phase transition
- Punctuated equilibrium
- Spontaneous symmetry breaking
- Snowball effect
参考资料
- ↑ E.C. Zeeman, Catastrophe Theory, Scientific American, April 1976; pp. 65–70, 75–83
- ↑ Cross, Daniel J., Zeeman's Catastrophe Machine in Flash
- ↑ Xu, F (1990). "Application of catastrophe theory to the ∆G≠ to -∆G relationship in electron transfer reactions". Zeitschrift für Physikalische Chemie. Neue Folge. 166: 79–91. doi:10.1524/zpch.1990.166.Part_1.079.
- ↑ Bełej, Mirosław; Kulesza, Sławomir (2012). "Modeling the Real Estate Prices in Olsztyn under Instability Conditions". Folia Oeconomica Stetinensia. 11 (1): 61–72. doi:10.2478/v10031-012-0008-7.
- ↑ A.O. Petters, H. Levine and J. Wambsganss, Singularity Theory and Gravitational Lensing", Birkhäuser Boston (2001)
参考书目
- Arnold, Vladimir Igorevich. Catastrophe Theory, 3rd ed. Berlin: Springer-Verlag, 1992.
- V. S. Afrajmovich, V. I. Arnold, et al., Bifurcation Theory And Catastrophe Theory.
- Bełej,M. Kulesza, S. Modeling the Real Estate Prices in Olsztyn under Instability Conditions. Folia Oeconomica Stetinensia. Volume 11, Issue 1, Pages 61–72, ISSN (Online) 1898-0198, ISSN (Print) 1730-4237, doi:10.2478/v10031-012-0008-7, 2013
- Castrigiano, Domenico P. L. and Hayes, Sandra A. Catastrophe Theory, 2nd ed. Boulder: Westview, 2004.
- Gilmore, Robert. Catastrophe Theory for Scientists and Engineers. New York: Dover, 1993.
- Petters, Arlie O., Levine, Harold and Wambsganss, Joachim. Singularity Theory and Gravitational Lensing. Boston: Birkhäuser, 2001.
- Postle, Denis. Catastrophe Theory – Predict and avoid personal disasters. Fontana Paperbacks, 1980.
- Poston, Tim and Stewart, Ian. Catastrophe: Theory and Its Applications. New York: Dover, 1998.
- Sanns, Werner. Catastrophe Theory with Mathematica: A Geometric Approach. Germany: DAV, 2000.
- Saunders, Peter Timothy. An Introduction to Catastrophe Theory. Cambridge, England: Cambridge University Press, 1980.
- Thom, René. Structural Stability and Morphogenesis: An Outline of a General Theory of Models. Reading, MA: Addison-Wesley, 1989.
- Thompson, J. Michael T. Instabilities and Catastrophes in Science and Engineering. New York: Wiley, 1982.
- Woodcock, Alexander Edward Richard and Davis, Monte. Catastrophe Theory. New York: E. P. Dutton, 1978.
- Zeeman, E.C. Catastrophe Theory-Selected Papers 1972–1977. Reading, MA: Addison-Wesley, 1977.
外部链接
类别: 分岔理论 类别: 奇点理论 范畴: 系统论 范畴: 混沌理论
编者推荐
知乎
CSDN社区
本中文词条由Moonscar、小饭编译,Inch审校,糖糖编辑,如有问题,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。