策略
在博弈论中,一个玩家的策略是他或她在一个情境下的选项,这个情境下的产出不仅取决于他们自己的行动,而且也取决于其他人的行动[1]。玩家的策略将决定玩家在博弈的任何阶段将采取的行动。
策略的概念有时(错误地)与移动的概念相混淆。移动是一个玩家在博弈过程中的某个时刻所采取的行动(例如,在国际象棋中,将白色的象移动到 从a2移动到b3)。另一方面,策略是进行博弈的整一套算法,告诉玩家在整个游戏中的每个可能情况下应该做什么。
策略配置(有时称为策略组合)是一套明确定义好博弈时所有玩家的所有行动的策略。一个策略配置必须给且只给每个球员配置一项策略。
策略集
玩家的策略集定义了他们在博弈时可以使用的策略。
如果一个玩家有几个可用的离散策略,那么他的策略集是有限的。例如,石头剪刀布游戏包括每个玩家的单次移动——每个玩家的移动都是在不知道对方的动作的情况下进行的,而不是一种反应——所以每个玩家都有一个有限的策略集{石头 剪刀 布}。
其他情况下策略集是无限的。例如,切蛋糕博弈的策略集是策略的一个有界连续体{切蛋糕切0%到100%之间的任何比例}。
在动态博弈中,策略集包含玩家安排机器人或代理人如何博弈的那些规则。例如,在最后通牒游戏中,第二个玩家的策略集包括接受哪些提议和拒绝哪些提议的所有可能规则。
在贝叶斯博弈中,策略集类似于动态博弈中的策略集。它包括对任何可能的私人信息采取何种行动的规则。
选择一个策略集
在应用博弈论中,博弈最好既可解又有意义。而策略集的定义就是实现这一艺术的重要组成部分。博弈理论家可以利用有关整体问题的知识来限制策略空间,并简化解决方案。
例如,严格地说,在最后通牒游戏中,玩家可以有以下策略: 拒绝($1,$3,$5,... ,$19) ,接受($0,$2,$4,... ,$20)。把所有这些战略都包括在内,会产生一个非常大的战略空间和一个有些困难的问题。博弈理论家可能相信他们可以将策略集限制为: { 对($0, $1, $2, ..., $20)中的x,拒绝所有 ≤ x的工作,接受任何一个 > x的工作。
单纯和混合策略
纯策略为玩家如何博弈提供了一个完整的定义。特别是,它决定了玩家面对所有可能情况下会进行的移动。都会采取的行动。一个玩家的策略集是该玩家可用的纯策略集。
混合策略是给每个纯策略设定一个概率。这允许玩家随机选择一个纯策略。(见以下部分的说明。)因为概率是连续的,所以一个参与人可以使用无限多的混合策略。
当然,我们可以把纯策略看作是混合策略的退化情形,在这种情形下,某个特定的纯策略的选择概率为1,而其他的策略的选择概率为0。
完全混合策略是一个混合策略,其中玩家为每个纯策略设定一个严格正的概率。(完全混合策略对于平衡细化非常重要,比如颤抖手完美均衡。)
混合策略
举例
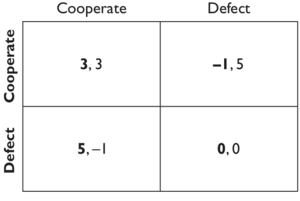
考虑右图的收益矩阵(称为协调博弈)。此时,一个玩家选择行,另一个玩家选择列。选择行的玩家获得第一项收益,选择列的玩家获得第二项收益。如果行玩家以概率1选择A(也就是说一定选择A) ,那么我们就说他是在玩纯策略。如果列玩家抛出一枚硬币,要是硬币正面朝上,选择 A,要是硬币反面朝上,就选择B,那么我们就说他是在玩一种混合策略,而不是纯策略。重要性
约翰·福布斯·纳什在他的著名论文中证明了每个有限博弈都存在均衡。我们可以把纳什均衡分为两种类型。纯策略纳什均衡是所有参与者都采用纯策略的纳什均衡。混合策略纳什均衡是至少有一个参与人采用混合策略时的均衡。虽然纳什证明了每个有限博弈都有纳什均衡点,但并不是所有的博弈都有纯策略纳什均衡。有关没有纯策略纳什均衡点的博弈的例子,请参阅匹配便士。然而,许多博弈确实存在纯策略纳什均衡(例如: 协调博弈,囚徒困境,猎鹿赛局)。此外,博弈可以同时具有纯策略均衡和混合策略均衡。一个简单的例子是纯协调博弈,其中除了纯策略(A,A)和(B,B)之外,还存在一个混合均衡,也就是两个参与者对每个策略都设定概率为1/2。
有争议的意义
在20世纪80年代,混合策略的概念因“直觉上有问题”而受到猛烈抨击[2] 。随机化是混合策略的核心,而它缺乏行为上的支持。很少有人按买彩票的方式做出选择。这个行为问题由于认知上的困难而变得更加复杂,人们在没有随机或伪随机发生器的帮助下无法产生随机结果[2]。
1991年,[3]博弈理论家阿里埃勒·鲁宾斯坦·马丁描述了理解这个概念的不同方式。第一种解释由哈萨尼(1973) [4]提出,被称为净化,它假定混合策略解释仅仅反映了我们对参与者的信息和决策过程的知识的缺乏。显然,随机的选择被看作是未指定的、与收益无关的外生因素的结果。然而,这种方式不令人满意,因为它的结果依赖于未指明的因素[3]。
第二种解释假设博弈玩家代表一大群代理人。每个代理人选择一个纯策略,收益取决于选择每个策略的代理人所占的比例。因此,混合策略代表了每个种群所选择的纯策略的分布。然而,当玩家是单个代理人时,它并不能为这种情况提供任何理由。
后来,奥曼 和 勃兰登堡 (1995)[5] 重新解释把纳什均衡点解释为信念的平衡,而不是行动的平衡。例如,在“石头剪刀布”中,信念的均衡会让每个玩家相信另一个玩家同样可能使用每种策略。然而,这种解释削弱了纳什均衡点的预测能力,因为在这样的均衡中,每个玩家都有可能真的使用石头的纯策略。
从那时起,博弈理论家对基于混合策略的结果的态度一直是矛盾的。混合策略仍然被广泛应用,因为它能在纯策略不存在均衡的博弈中提供纳什均衡,但是这个模型并没有说明为什么以及参与者如何随机化他们的决策。
行为策略
当混合策略在纯策略之上设定一个概率分布/值时,行为策略在每个信息集上分配一个可能行动集的概率分布。尽管这两个概念在正则形式博弈的背景下是密切相关的,但是它们对于广泛形式的博弈有着非常不同的含义。粗略地说,混合策略通过博弈树随机选择一条确定性路径,而行为策略可以看作是一条随机路径。
混合策略和行为策略之间的关系是库恩定理的主题。这一结果表明,在任何具有完美回忆的有限广义博弈中,对于任何玩家和任何混合策略,都存在一种行为策略,该策略针对(其他玩家的)所有策略配置在终端节点上引起与混合策略相同的分布。反之亦然。
匹兹堡 和 鲁宾斯坦 (1997)用他们的 "心不在焉的司机" 博弈给出了一个著名的例子,说明为什么要求完全回忆的等价性。
另请参见
参考文献
- ↑ Ben Polak, Game Theory: Lecture 1 Transcript ECON 159, 5 September 2007, Open Yale Courses.
- ↑ 2.0 2.1 Aumann, R. (1985). "What is Game Theory Trying to accomplish?". In Arrow, K.; Honkapohja, S.. Frontiers of Economics. Oxford: Basil Blackwell. pp. 909–924. http://www.ma.huji.ac.il/raumann/pdf/what%20is%20game%20theory.pdf.
- ↑ 3.0 3.1 Rubinstein, A. (1991). "Comments on the interpretation of Game Theory". Econometrica. 59 (4): 909–924. doi:10.2307/2938166. JSTOR 2938166.
- ↑ Harsanyi, John (1973). "Games with randomly disturbed payoffs: a new rationale for mixed-strategy equilibrium points". Int. J. Game Theory. 2: 1–23. doi:10.1007/BF01737554.
- ↑ Aumann, Robert; Brandenburger, Adam (1995). "Epistemic Conditions for Nash Equilibrium". Econometrica. 63 (5): 1161–1180. CiteSeerX 10.1.1.122.5816. doi:10.2307/2171725. JSTOR 2171725.
编者推荐

下为一些链接(源于集智俱乐部公众号)能够更好的了解博弈论的相关信息: 来自YouTube上面的Complexity Labs(Complexity Labs是一个专门介绍复杂系统领域知识的在线学习网站)
来自集智学园关于博弈论的相关课程
此外,还有根据纳什的传记改编的电源
- 本书在对风险领域研究的开创性意义方面值得关注。丹·加德纳作为一位资深的媒体记者,能够静下心来系统探讨关乎人们身心健康的风险与恐惧问题,着实不易,而丹·加德纳却令人信服地做到了。
本中文词条由舒寒翻译,Fernando审校,薄荷编辑,如有问题,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。