算法分析
在计算机科学中,算法分析 analysis of algorithms是计算查找算法复杂性的过程——包括算法执行时间、所需存储空间或其他资源的数量。通常这是一个确定函数,该函数将一个算法的输入长度与所需的迭代步数(时间复杂度)或使用的存储大小(空间复杂度)相关联。当某个算法其算法复杂性函数的取值很小,或者其函数值大小的增长速度与算法输入大小的相比更加缓慢时,我们认为该算法是有效的。相同长度的不同输入可能导致算法表现出不同的效果,因此对算法运行的最佳、最差和平均情况的描述都可能具有一定的实际意义。但是当没有特殊说明时,算法性能描述函数通常反映的是算法复杂性一种上界,由算法表现最差情况的输入来确定。
“算法分析”这个术语是由 Donald Knuth 提出的。[1]算法分析是广义计算复杂性理论的重要组成部分,它为任何解决给定计算问题的算法所需的资源提供理论估计。这些估计为有效算法的合理性评价提供了思路。
在算法的理论分析中,通常是在渐近意义上估计它们的复杂性,即对任意大输入的复杂度函数进行估计。为了达到这个目的,我们使用到了大O符号、大Ω符号和大θ符号。例如,二进制搜索被称为以与“被搜索的排序列表长度的对数成正比”的若干步长来运行,或者用O(log(n))表示,通俗地说就是“以对数时间”运行。之所以我们通常使用渐近估计,是因为同一算法的不同实现的算法效率表现会有所不同。然而,给定算法的任何两个“合理”实现的效率,是由一个称为“隐常数 a hidden constant”的常数乘法因子相关联的。
算法效率的精确(这里就不是渐近了)度量有时是可以计算的,但它们通常需要一定的关于算法特定实现的假设,这种算法被称为计算模型。一个计算模型可以用抽象计算机来定义,例如图灵机,和 / 或通过假设某些操作在单位时间内执行。
例如,如果我们应用二分法搜索的待排序列表有 n 个元素,并且我们可以保证列表中每个元素的查找都可以在单位时间内完成,那么最多需要 log2 n + 1 的时间就可以得到返回值结果。
成本模型
时间效率的估计取决于我们对步骤的定义。为了使分析有效地对应于实际执行时间,执行一个步骤所需的时间必须保证一个常数。这里需要注意的是,例如,有些分析把两个数字的相加计算为一个步骤。在某些情况下,这种假设可能是不正当的。例如,如果计算中涉及的数字可能是任意大的,那么单个加法所需的时间就不能再假定为常数。
- 统一成本模型:也称为“统一成本计量”(和类似的变体),为每台机器操作分配一个固定的算法消耗,与涉及的数量大小无关;
- 对数成本模型:也称为“对数成本测量”(及类似变体),为每台机器操作分配一个与所涉及的位数成比例的成本;
后者使用起来比较麻烦,所以只有在必要的时候才会使用,例如在分析高精度计算算法时,就像那些在密码学中使用的算法。
而一个经常被我们忽略的关键点是,常见问题的下界通常是给定一个计算模型,这个模型比你在实践中可以使用的操作集更加有限,因此存在一些算法的效率比我们认为的下界要更快。[7]
运行时分析
运行时分析是一种理论分类,它得出的算法预期运行时间(或运行时间)是随着算法输入大小(通常表示为n)的增加而增加的。运行时效率是计算机科学中一个热门话题: 一个程序究竟是需要几秒钟还是几小时甚至几年才能完成执行,这取决于它具体实现的方法。虽然软件分析技术可用于在实践中测量算法的运行时间,但它们不能为所有无限多可能的输入提供计时数据; 后者只能通过运行时间分析的理论方法来实现。
经验指标的缺陷
由于算法与平台无关(即一个给定的算法,可以在任意运行任意操作系统的计算机上用任意编程语言实现),使用经验方法来衡量一组给定算法的比较性能还有一个明显的缺点。
举个例子,一个程序在一个大小为n的排序列表中查找一个特定的条目。假设这个程序是在A计算机上实现的,计算机A是最先进的机器,使用线性搜索算法,而计算机B使用二分法进行搜索,但是B计算机本身的运行速度要慢得多。两台计算机分别运行该程序的基准测试结果如下所示:
| n (列表大小) | 计算机A运算时间(毫秒) | 计算机B运算时间(毫秒) |
|---|---|---|
| 16 | 8 | 100,000 |
| 63 | 32 | 150,000 |
| 250 | 125 | 200,000 |
| 1,000 | 500 | 250,000 |
基于这些度量,我们很容易得出结论:计算机A运行的算法在效率上远远优于计算机B。然而,如果输入列表的大小增加到一个足够大的数字,这个结论就会发生戏剧性的反转。
| n (列表大小) | 计算机A运算时间(毫秒) | 计算机B运算时间(毫秒) |
|---|---|---|
| 16 | 8 | 100,000 |
| 63 | 32 | 150,000 |
| 250 | 125 | 200,000 |
| 1,000 | 500 | 250,000 |
| ... | ... | ... |
| 1,000,000 | 500,000 | 500,000 |
| 4,000,000 | 2,000,000 | 550,000 |
| 16,000,000 | 8,000,000 | 600,000 |
| ... | ... | ... |
| 63,072 × 1012 | 31,536 × 1012 ns, or 1 year |
1,375,000 ns, or 1.375 毫秒 |
运行线性搜索程序的计算机A的效率呈现线性增长,即程序的运行时间与其输入大小成正比,也就是说将输入大小增加一倍时运行时间也将增加一倍,将输入大小增加四倍则运行时间也会增加四倍等等。另一方面,运行二分法搜索程序的计算机B的效率呈现出对数增长趋势,将输入大小变成原来的两倍只会使运行时增加一个常量(在本例中为50,000 ns)。尽管从表面上看计算机A是一台速度更快的机器,但计算机B在运行时势必会地超过计算机A,因为它运行的算法增长速度要慢得多。
生长规律
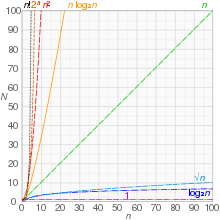
非正式地,一个算法可以说表现出一个数学函数级的增长率,如果超过一定的输入大小n,函数乘以一个正常数为该算法的运行时间提供了一个上限或极限。换言之,对于给定的输入大小n大于某个n0和常数c,该算法的运行时间永远不会大于。这个概念经常使用大写字母O符号表示。例如,由于插入排序的运行时随着其输入大小的增加而二次增长,因此插入排序的时间复杂度可以表示为O(n2)。
对于给定的算法,大O表示法是表达算法最坏情况的一种简便方法,尽管它也可以用来表示平均情况-例如,快速排序的最差表现是O(n2) ,但是平均情况下其运行时是O(n log n)。
经验增长规律
假设算法运行时间遵循幂律规则,t ≈ k na,系数a可以通过对一些问题规模点[math]\displaystyle{ \{n_1, n_2\} }[/math]的运行时间[math]\displaystyle{ \{t_1, t_2\} }[/math]进行经验测量,并计算出𝑡[math]\displaystyle{ t_2/t_1 = (n_2/n_1)^a }[/math],从而得到系数[math]\displaystyle{ a = \log(t_2/t_1) / \log(n_2/n_1) }[/math]。 换言之,这衡量了在某个规模点上,执行时间与问题大小的双对数曲线 log-log plot上经验线的斜率。如果增长顺序确实遵循幂律(因此双对数曲线图上的直线确实是一条直线),那么a的经验值将在不同的范围内将保持不变,如果不是,它将发生改变(而且这条线是一条曲线),但仍然可以用来比较任何两种给定算法的经验局部增长顺序。应用于下表:
| n (列表大小) | 计算机A运算时间(毫秒) | 本地增长顺序 (n^_) |
计算机B运算时间(毫秒) | 本地增长顺序 (n^_) |
|---|---|---|---|---|
| 15 | 7 | 100,000 | ||
| 65 | 32 | 1.04 | 150,000 | 0.28 |
| 250 | 125 | 1.01 | 200,000 | 0.21 |
| 1,000 | 500 | 1.00 | 250,000 | 0.16 |
| ... | ... | ... | ||
| 1,000,000 | 500,000 | 1.00 | 500,000 | 0.10 |
| 4,000,000 | 2,000,000 | 1.00 | 550,000 | 0.07 |
| 16,000,000 | 8,000,000 | 1.00 | 600,000 | 0.06 |
| ... | ... | ... |
可以清楚地看到,第一个算法展示了一个线性增长的序列,这确实遵循幂规则。第二个经验值正在迅速递减,这表明它遵循了另一条增长规律,而且无论如何,从经验上看,其当下的增长(及其进一步的增长)远低于第一个。
运行时复杂性度量
给定算法的最差运行复杂度有时可以通过检查算法的结构和做一些简化的假设来进行评估。例如下面这段伪代码:
1 get a positive integer n from input 2 if n > 10 3 print "This might take a while..." 4 for i = 1 to n 5 for j = 1 to i 6 print i * j 7 print "Done!"
一台给定的计算机在执行算法有关的每一条指令时花费的时间是离散的。执行给定指令的具体时间量取决于正在执行的指令和正在执行的计算机,但在传统计算机上,这个时间量是确定的。假设在步骤1中执行的操作消耗时间为T1,步骤2的时间为T2,依此类推。
在上面的算法中,步骤1、2和7只运行一次。对于最坏情况的评估,应该假定步骤3也将运行。因此,运行步骤1-3和步骤7所需的总时间是:
- [math]\displaystyle{ T_1 + T_2 + T_3 + T_7. \, }[/math]
步骤4、5和6中的循环更难计算。步骤4中的外部循环测试将执行(n + 1)次(注意,终止 for 循环需要一个额外的步骤,因此循环次数是 n + 1 次而不是 n次),这将消耗时间T4( n+1)。另一方面,内部循环由变量 j 的值控制,取值范围为 1 到 i。在第一次通过外循环时,j从1迭代到1:内循环进行一次传递,因此运行内循环(步骤6)消耗时间T6,内循环测试(步骤5)消耗时间为2T5。在下一次通过外部循环时,j 从1迭代到2: 内部循环进行两次后结束,因此运行内部循环体(步骤6)消耗时间为2T6,而内部循环测试(步骤5)消耗的时间为3T5。
总之,运行内部循环体所需的总时间可以用等差数列表示:
- [math]\displaystyle{ T_6 + 2T_6 + 3T_6 + \cdots + (n-1) T_6 + n T_6 }[/math]
可以整理成:
- [math]\displaystyle{ T_6 \left[ 1 + 2 + 3 + \cdots + (n-1) + n \right] = T_6 \left[ \frac{1}{2} (n^2 + n) \right] }[/math]
运行外部循环测试所需的总时间也可以用类似的方法来计算:
- [math]\displaystyle{ \begin{align} & 2T_5 + 3T_5 + 4T_5 + \cdots + (n-1) T_5 + n T_5 + (n + 1) T_5\\ =\ &T_5 + 2T_5 + 3T_5 + 4T_5 + \cdots + (n-1)T_5 + nT_5 + (n+1)T_5 - T_5 \end{align} }[/math]
进一步整理为:
- [math]\displaystyle{ \begin{align} & T_5 \left[ 1+2+3+\cdots + (n-1) + n + (n + 1) \right] - T_5 \\ =& \left[ \frac{1}{2} (n^2 + n) \right] T_5 + (n + 1)T_5 - T_5 \\ =& T_5 \left[ \frac{1}{2} (n^2 + n) \right] + n T_5 \\ =& \left[ \frac{1}{2} (n^2 + 3n) \right] T_5 \end{align} }[/math]
因此,此算法的总运行时间为:
- [math]\displaystyle{ f(n) = T_1 + T_2 + T_3 + T_7 + (n + 1)T_4 + \left[ \frac{1}{2} (n^2 + n) \right] T_6 + \left[ \frac{1}{2} (n^2+3n) \right] T_5 }[/math]、
可以简化为:
- [math]\displaystyle{ f(n) = \left[ \frac{1}{2} (n^2 + n) \right] T_6 + \left[ \frac{1}{2} (n^2 + 3n) \right] T_5 + (n + 1)T_4 + T_1 + T_2 + T_3 + T_7 }[/math]
根据经验法则 Rule-of-thumb,我们可以假设任意给定函数中的最高阶项主导其增长率,从而定义其运行时顺序。在这个例子中,最高阶项为n2,因此可以得出f(n) = O(n2)。证明如下:
证明:[math]\displaystyle{ \left[ \frac{1}{2} (n^2 + n) \right] T_6 + \left[ \frac{1}{2} (n^2 + 3n) \right] T_5 + (n + 1)T_4 + T_1 + T_2 + T_3 + T_7 \le cn^2,\ n \ge n_0 }[/math]
[math]\displaystyle{ \begin{align}
&\left[ \frac{1}{2} (n^2 + n) \right] T_6 + \left[ \frac{1}{2} (n^2 + 3n) \right] T_5 + (n + 1)T_4 + T_1 + T_2 + T_3 + T_7\\
\le &( n^2 + n )T_6 + ( n^2 + 3n )T_5 + (n + 1)T_4 + T_1 + T_2 + T_3 + T_7 \ (\text{for } n \ge 0 )
\end{align} }[/math]
设k为一个大于或等于[T1..T7]的常数:
[math]\displaystyle{ \begin{align}
&T_6( n^2 + n ) + T_5( n^2 + 3n ) + (n + 1)T_4 + T_1 + T_2 + T_3 + T_7 \le k( n^2 + n ) + k( n^2 + 3n ) + kn + 5k\\
= &2kn^2 + 5kn + 5k \le 2kn^2 + 5kn^2 + 5kn^2 \ (\text{for } n \ge 1) = 12kn^2
\end{align} }[/math]
因此:
[math]\displaystyle{ \left[ \frac{1}{2} (n^2 + n) \right] T_6 + \left[ \frac{1}{2} (n^2 + 3n) \right] T_5 + (n + 1)T_4 + T_1 + T_2 + T_3 + T_7 \le cn^2, n \ge n_0 \text{ for } c = 12k, n_0 = 1 }[/math]
分析这个算法的一个更好的方法,是声明[T1..T7]都等于一个时间单位,在同一个单位制中,选择这样一个单位大于或等于这些步骤的实际时间。这意味着该算法的运行时间分解如下:
[math]\displaystyle{ 4+\sum_{i=1}^n i\leq 4+\sum_{i=1}^n n=4+n^2\leq5n^2 \ (\text{for } n \ge 1) =O(n^2). }[/math]
其他资源增长率分析
运行时分析的方法也可用于预测其他增长率,如内存空间的消耗。例如下面的这个伪代码,它表示根据程序管理的文件大小来管理和重新分配程序的内存使用:
while file is still open:
let n = size of file
for every 100,000 kilobytes of increase in file size
double the amount of memory reserved
在这个例子中,随着文件大小 n 的增加,内存消耗的速度将达到指数增长,即O(2n)。对于内存资源的消耗来讲,这种量级的增长率是很大的并且很有可能无法控制。
意义
算法分析在实践中非常重要,因为偶然或无意地使用低效算法会显著影响系统性能。在对时间敏感的应用程序中,运行时间过长的算法可能使其结果过时或无用。一个低效的算法也可能最终需要不经济的计算能力或存储量才能运行,再一次使它变得毫无用处。
常数因子
算法的分析通常侧重于算法的渐近性能,尤其是在初级阶段,但在实际应用中,常系数非常重要,但实际数据的大小往往是有限的。该限制通常表现为是可寻址内存的大小,因此在32位计算机上232 = 4 GiB(如果使用分段内存,则更大),在64位计算机上264 = 16 EiB。因此,给定一个有限的大小,一个增长的顺序(时间或空间)可以被一个常数因子代替,在这个意义上,所有实际的算法对于足够大的常数或足够小的数据都是O(1)。
这种解释主要适用于增长极慢的函数:(二进制)所有实际数据(265536位)的迭代对数(log*)小于5;(二进制)对数对数(log log n)对于几乎所有实际数据(264位)小于6;对于几乎所有实际数据(264位),二进制对数(log n)小于64。然而,如果恒定时间算法的开销导致更大的常数因子,则具有非恒定复杂度的算法在实际数据上可能比具有恒定复杂度的算法更有效,例如,只要[math]\displaystyle{ K/k \gt 6 }[/math]且[math]\displaystyle{ n \lt 2^{2^6} = 2^{64} }[/math],则可以具有[math]\displaystyle{ K \gt k \log \log n }[/math]。
对于大数据来讲,线性或二次项系数是不能忽略的,但对于小数据,渐近低效的算法可能更有效。这尤其适用于混合算法,如Timsort,它使用渐近有效的算法(这里指归并排序,时间复杂度[math]\displaystyle{ n \log n }[/math]),但对于小数据,转换为渐近低效的算法(这里是插入排序,时间复杂度为[math]\displaystyle{ n^2 }[/math]),因为简单算法在小数据上更快。
参见
参考文献
- ↑ "Knuth: Recent News". web.archive.org. 28 August 2016.
- ↑ Alfred V. Aho; John E. Hopcroft; Jeffrey D. Ullman (1974). The design and analysis of computer algorithms. Addison-Wesley Pub. Co.. https://archive.org/details/designanalysisof00ahoarich., section 1.3
- ↑ Juraj Hromkovič (2004). Theoretical computer science: introduction to Automata, computability, complexity, algorithmics, randomization, communication, and cryptography. Springer. pp. 177–178. ISBN 978-3-540-14015-3. https://books.google.com/books?id=KpNet-n262QC&pg=PA177.
- ↑ Giorgio Ausiello (1999). Complexity and approximation: combinatorial optimization problems and their approximability properties. Springer. pp. 3–8. ISBN 978-3-540-65431-5. https://books.google.com/books?id=Yxxw90d9AuMC&pg=PA3.
- ↑ Wegener, Ingo (2005), Complexity theory: exploring the limits of efficient algorithms, Berlin, New York: Springer-Verlag, p. 20, ISBN 978-3-540-21045-0
- ↑ Robert Endre Tarjan (1983). Data structures and network algorithms. SIAM. pp. 3–7. ISBN 978-0-89871-187-5. https://books.google.com/books?id=JiC7mIqg-X4C&pg=PA3.
- ↑ Examples of the price of abstraction?, cstheory.stackexchange.com
- Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L. & Stein, Clifford (2001). Introduction to Algorithms. Chapter 1: Foundations (Second ed.). Cambridge, MA: MIT Press and McGraw-Hill. pp. 3–122. ISBN 0-262-03293-7.
- Sedgewick, Robert (1998). Algorithms in C, Parts 1-4: Fundamentals, Data Structures, Sorting, Searching (3rd ed.). Reading, MA: Addison-Wesley Professional. ISBN 978-0-201-31452-6. https://archive.org/details/algorithmsinc00sedg.
- Knuth, Donald. The Art of Computer Programming. Addison-Wesley.
- Greene, Daniel A.; Knuth, Donald E. (1982). Mathematics for the Analysis of Algorithms (Second ed.). Birkhäuser. ISBN 3-7643-3102-X.
- Goldreich, Oded (2010). Computational Complexity: A Conceptual Perspective. Cambridge University Press. ISBN 978-0-521-88473-0.
编者推荐
集智文章
彭兰:算法社会的“囚徒”风险
今天算法的应用正在全面普及,一个算法社会正在到来。人们在享受算法带来的便利的同时,在某些方面也面临着成为算法“囚徒”的风险。人的认知、判断与决策可能会受制于算法,人的社会位置也会因算法偏见、歧视以及其他原因受到禁锢。在一些数字劳动平台,算法在隐性控制着劳动者的劳动,算法、大数据及其他新技术也可能增强对人的监控。但反思算法社会的“囚徒”风险,并不意味对算法的拒绝,加强算法开发者的技术理性和算法伦理培养,提高算法应用者的算法素养,我们才能更好地应对算法社会的挑战。
本篇节选自由中国人民大学新闻学院的彭兰教授写的《算法社会的“囚徒”风险》文章。
相关文章
本中文词条由薄荷编辑,如有问题,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。