网络模块化

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
跳到导航 跳到搜索


该词条由Dawn翻译、编辑，由Elena审校，【张江】总审校，翻译自Wikipedia词条Modularity



Modularity（模块化）是network（网络）或graph（图形）结构的一种度量，用于衡量网络划分为模块（也称为组，集群或社团）的强度。具有高模块化的网络在模块内的节点之间具有密集连接，但在不同模块的节点之间具有稀疏连接。在检测网络中community structure（社团结构）的优化方法中常使用模块化。但是，模块化受到分辨率限制，因此无法检测小社团。生物网络，包括动物的大脑，具有高度的模块化。


动机

许多科学领域中的重要问题可以用网络来表示或进行实证研究。例如，生物和社会模式，万维网，代谢网络，食物网，神经网络和病理网络，这些现实世界中的问题都可以通过数学表示和拓扑研究来发现一些意想不到的结构特征[1]。其中的大多数网络都具有某种社团结构，这对理解网络的动态具有重要意义，比如一个密切联系的社交社团意味着他们之间的信息或谣言传播速度要快于松散联系的社团。因此，如果网络由通过链路连接的多个单独节点表示，其中链路表示节点之间的某种程度的交互，则社团被定义为内部节点稠密互连，但仅与网络的其余部分稀疏连接的组。因此，确定网络中的社团往往是必要的，因为社团可能具有与普通网络完全不同的属性，如节点度，聚类系数，中介性，中心性[2]等等。模块化就是确定社团的一种方式，在最大化模块化时，会导致特定网络中社团的出现。


定义

当边满足随机分布时，模块化的值是落在给定组内的边的分数减去预期分数，模块化的值在[math]\displaystyle{ [-1,1] }[/math]的范围内[3]。若组内边的数量超过基于偶然性的预期数量，则模块化值为正。对于网络顶点到某些模块的给定划分，模块化反映了模块内边的集中度与所有节点之间链路随机分布的对比，而非模块本身。

计算模块化的方法有很多[1]。在该概念最通用的版本中，总是对边进行随机化以便保持每个顶点的degree(度)。我们考虑一个有[math]\displaystyle{ n }[/math]个node(节点)和[math]\displaystyle{ m }[/math]条链路（边）的图，它可以通过成员变量[math]\displaystyle{ s }[/math]划分为两个社团。如果节点[math]\displaystyle{ v }[/math]属于社团1，[math]\displaystyle{ s_v = 1 }[/math]，反之，若[math]\displaystyle{ v }[/math]属于社团2，则[math]\displaystyle{ {s_v} = -1 }[/math]。网络的adjacency matrix(邻接矩阵)用[math]\displaystyle{ A }[/math]表示，其中，[math]\displaystyle{ A_{{vw}}=0 }[/math]意味着节点[math]\displaystyle{ v }[/math]和[math]\displaystyle{ w }[/math] 之间没有边（没有交互），[math]\displaystyle{ A_{{vw}}=1 }[/math]意味着两者之间存在边。为简单起见，考虑一个无向网络，则[math]\displaystyle{ A_{{vw}} = A_{{wv}} }[/math]。（重要的是要注意两个节点之间可能存在多条边，但在此我们只考虑最简单的情况）。

那么，模块化Q被定义为落入组1或组2内的边的分数，减去组1和2内具有与给定网络相同节点度分布的随机图的预期边数量。

预期的边数量可以使用配置模型的概念计算[4]，配置模型是特定网络的随机实现。给定一个具有[math]\displaystyle{ n }[/math]个节点的网络，其中每个节点[math]\displaystyle{ v }[/math]具有节点度为[math]\displaystyle{ k_v }[/math]，配置模型将每个边切割成两半，然后每个半边（也称为存根）随机地与网络中的任何其他存根重新连接，甚至允许自循环。因此，配置模型能在保持图的节点度分布不变的情况下构建完全随机的网络。

假设总存根数为[math]\displaystyle{ l_n }[/math]，那么：

[math]\displaystyle{ l_{n}= \sum_{v} k_{v} =2m. \qquad(1) }[/math]

现在，随机选取两个节点[math]\displaystyle{ v }[/math]和[math]\displaystyle{ w }[/math]，它们的节点度分别为[math]\displaystyle{ k_v }[/math]，[math]\displaystyle{ {k_w} }[/math]，重新用存根将两节点连接，那么：

[math]\displaystyle{ \text{Expectation of full edges between }v \text{ and }w =\frac{\text{ (Full edges between }v\text{ and }w\text{)}}{ \text{(Total number of rewiring possibilities)}}. \qquad(2) }[/math]

可能重新连接的接线总数等于选择特定存根后剩余的存根数[math]\displaystyle{ {l_{n-1}} }[/math]，当[math]\displaystyle{ n }[/math]很大时，[math]\displaystyle{ \ l_{n-1}\approx l_n }[/math]，故有：

[math]\displaystyle{ \text{Expected number of full edges between }v\text{ and }w = \frac{k_v k_w}{l_n} = \frac{k_v k_w}{2m} }[/math]

因此，节点[math]\displaystyle{ v }[/math]和[math]\displaystyle{ w }[/math]之间的实际边的数量与它们之间预期边的数量之间的差异值为：

[math]\displaystyle{ A_{vw} - \frac{k_v k_w}{2m} }[/math]

对所有节点对求和得到模块化值Q的计算公式[1]：

[math]\displaystyle{ Q = \frac{1}{2m} \sum_{vw} \left[ A_{vw} - \frac{k_v k_w}{2m} \right] \frac{s_{v} s_{w}+1}{2}. \qquad(3) }[/math]

注意，等式(3)仅适用于将网络划分为两个社团的情况。分层划分（即先划分为两个社团，然后将两个子社团进一步划分为两个较小的子社团，只需最大化Q）是将网络划分为多个社团的可行方法。此外，等式(3)可以推广到将网络划分为c个社团[5]。

[math]\displaystyle{ Q = \frac{1}{(2m)}\sum_{vw} \left[ A_{vw} - \frac{k_v k_w}{(2m)} \right] \delta(c_{v}, c_{w}) =\sum_{i=1}^{c} (e_{ii}-a_{i}^2). \qquad(4) }[/math]

其中，eij为一个末端顶点在社团i，另一个末端顶点在社团j的边的分数：

[math]\displaystyle{ e_{ij}= \sum_{vw} \frac{A_{vw}}{2m} 1_{v\in c_i} 1_{w\in c_j} }[/math]

而ai是连接到社团i中的顶点的边的末端分数：

[math]\displaystyle{ a_i=\frac{k_i}{2m} = \sum_{j} e_{ij} }[/math]

多社团检测实例

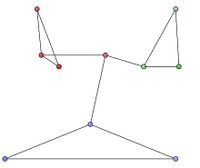
我们考虑一个由10个节点，12条边组成且对应以下邻接矩阵的无向网络。

图1 网络示例 10个节点，12条边且对应左侧的邻接矩阵
图2 最大化Q值的网络分区示例图 Qmax=0.4896
节点 ID 1 2 3 4 5 6 7 8 9 10
1 0 1 1 0 0 0 0 0 0 1
2 1 0 1 0 0 0 0 0 0 0
3 1 1 0 0 0 0 0 0 0 0
4 0 0 0 0 1 1 0 0 0 1
5 0 0 0 1 0 1 0 0 0 0
6 0 0 0 1 1 0 0 0 0 0
7 0 0 0 0 0 0 0 1 1 1
8 0 0 0 0 0 0 1 0 1 0
9 0 0 0 0 0 0 1 1 0 0
10 1 0 0 1 0 0 1 0 0 0

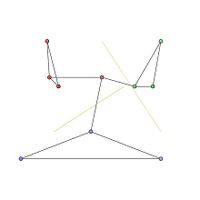
图1中，红色、绿色和蓝色节点组成的集群分别表示不同的社团。优化社团分区如图2所示。


矩阵表述

模块化的另一种在频谱优化算法中常用的替代公式，如下所述[1]。假设当顶点v属于组r时，Svr为1，否则为0。那么：

[math]\displaystyle{ \delta(c_v,c_w) = \sum_r S_{vr} S_{wr} }[/math]

因此，

[math]\displaystyle{ Q = \frac{1}{2m} \sum_{vw} \sum_r \left[ A_{vw} - \frac{k_v k_w}{2m} \right] S_{vr} S_{wr} = \frac{1}{2m} \mathrm{Tr}(\mathbf{S}^\mathrm{T}\mathbf{BS}), }[/math]

其中，S是具有元素Svr和B的（非方块）矩阵，即所谓的模块化矩阵，它有元素

[math]\displaystyle{ B_{vw} = A_{vw} - \frac{k_v k_w}{2m}. }[/math]

模块化矩阵的所有行和列总和为零，这意味着未分割网络的模块化的值也始终为零。

对于划分成两个社团的网络，通过定义sv = ±1来表示节点v所属的社团，于是

[math]\displaystyle{ Q = {1\over 4m} \sum_{vw} B_{vw} s_v s_w = {1\over 4m} \mathbf{s}^\mathrm{T}\mathbf{Bs}, }[/math]

其中s是具有元素sv的列向量[1]。

此函数与Ising（伊辛）spin glass（自旋玻璃）的Hamiltonian（哈密顿量）具有相同的形式，利用一个连接来创建简单的计算机算法，例如使用simulated annealing（模拟退火算法），从而最大化模块化。任意数量社团的模块化的一般形式则等同于Potts自旋玻璃，同样可开发类似的算法[6]。


分辨率限制

模块化是集群中边的数目与 若有一个与指定网络具有相同节点数且每个节点的度与原网络保持一致，但网络中的边随机连接的随机网络，那么，模块化是原集群中边的数目与随机网络的集群所期望的边数目的对比。其中，该随机零模型隐含地假设了每个节点可以连接到网络的任何节点。然而，此假设在网络非常大时是不合理的，因为节点的范围只包括了网络的一小部分，而忽略了大部分网络。这也意味着随着网络变大，两个组的节点之间的预期边数量将减少。当网络足够大时，模块化的零模型中两个组的节点之间的预期边数甚至可能小于1。在这种情况下，两个集群之间单条边的连接将被模块化解释为两个集群之间强相关性的标志，且优化模块化将导致两个集群的合并，而此过程未考虑到集群本身的特征。因此，对于弱互连的完整图，只要它们具有最高可能的内部边密度，且表示最佳可识别的社团，那么当网络足够大时，模块化优化算法也将对这些图进行合并[7]。出于这个原因，在大型网络中即使对社团进行良好定义，模块化优化算法仍然无法解决小型社团的情况。在诸如模块化优化算法这种依赖于全局零模型的方法中，这个偏差是不可避免的[8]。


多分辨率方法

解决模块化中的分辨率限制问题主要有两种方法：以自循环的形式向每个节点添加电阻r，让增加（r>0）或减小（r<0）的两类节点分别形成社团[9]; 或在模块化定义中，当空案例时，在前面添加参数γ>0，用它控制社团内部连接和空模型之间的相对重要性[6]。在这些参数各自适当的范围内，通过优化模块化调整参数值，这可以覆盖整个网络的中尺度，从所有节点属于同一社团的宏观尺度，到每个节点属于各自社团的微观尺度，因此称为多分辨率方法。但是，当社团规模差异较大时，这些方法具有局限性[10]。


参见

参考文献

  1. ↑ 1.0 1.1 1.2 1.3 1.4 Newman, M. E. J. (2006). "Modularity and community structure in networks". Proceedings of the National Academy of Sciences of the United States of America. 103 (23): 8577–8696. arXiv: physics/0602124  .Bibcode:2006PNAS..103.8577N. doi:10.1073/pnas.0601602103. PMC 1482622 . PMID 16723398.
  2. ↑ Newman, M. E. J. (2007). Palgrave Macmillan, Basingstoke, eds. "Mathematics of networks". The New Palgrave Encyclopedia of Economics (2 ed.).
  3. ↑ Li, Wenye; Schuurmans, Dale (2011). "Modular Community Detection in Networks". IJCAI Proceedings-International Joint Conference on Artificial Intelligence. 22 (1): 2. doi:10.5591/978-1-57735-516-8/IJCAI11-231.
  4. ↑ van der Hofstad, Remco (2013). "Chapter 7". Random Graphs and Complex Networks (PDF).
  5. ↑ Clauset, Aaron and Newman, M. E. J. and Moore, Cristopher (2004). "Finding community structure in very large networks". Phys. Rev. E. 70 (6): 066111. arXiv: cond-mat/0408187 . Bibcode: 2004PhRvE..70f6111C. doi:10.1103/PhysRevE.70.066111.
  6. ↑ 6.0 6.1 Joerg Reichardt & Stefan Bornholdt (2006). "Statistical mechanics of community detection". Physical Review E. 74 (1): 016110. arXiv:cond-mat/0603718. Bibcode: 2006PhRvE..74a6110R.doi:10.1103/PhysRevE.74.016110.
  7. ↑ Santo Fortunato & Marc Barthelemy (2007). "Resolution limit in community detection". Proceedings of the National Academy of Sciences of the United States of America. 104 (1): 36–41. arXiv:physics/0607100. Bibcode: 2007PNAS..104...36F.doi:10.1073/pnas.0605965104. PMC 1765466. PMID 17190818.
  8. ↑ J.M. Kumpula; J. Saramäki; K. Kaski & J. Kertész (2007). "Limited resolution in complex network community detection with Potts model approach". European Physical Journal B. 56 (1): 41–45. arXiv:cond-mat/0610370. Bibcode: 2007EPJB...56...41K.doi:10.1140/epjb/e2007-00088-4.
  9. ↑ Alex Arenas, Alberto Fernández and Sergio Gómez (2008). "Analysis of the structure of complex networks at different resolution levels". New Journal of Physics. 10 (5): 053039. arXiv:physics/0703218. Bibcode: 2008NJPh...10e3039A.doi:10.1088/1367-2630/10/5/053039.
  10. ↑ Andrea Lancichinetti & Santo Fortunato (2011). "Limits of modularity maximization in community detection". Physical Review E. 84: 066122. arXiv:1107.1155. Bibcode: 2011PhRvE..84f6122L.doi:10.1103/PhysRevE.84.066122.


相关链接

本词条内容翻译自 en.wikipedia.org，遵守 CC3.0协议。

取自“https://wiki.swarma.org/index.php?title=网络模块化&oldid=15501”