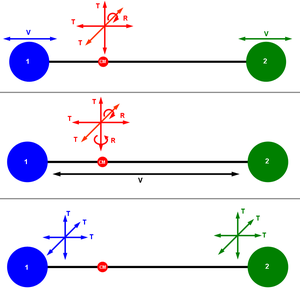
自由度

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
跳到导航 跳到搜索

在物理和化学中，自由度 Degree of freedom指的是形式化描述某一物理系统的状态时，一个独立的物理量。某一系统所有状态的集合称为该系统的相空间 Phase space，该系统的自由度便是相空间的维数。

粒子 particle 在三维 three-dimensional 空间中的位置需要三个位置坐标来标识。 同样地，我们也能够根据三个速度分量来描述粒子运动的方向和速度，每个速度分量都参照该空间的三个维度。 如果系统的时间演变是确定的，其中某一时刻的状态唯一地确定其过去和未来的位置和速度随时间的变化，则该系统具有六个自由度。如果将粒子的运动限制在更低的维度，例如，粒子必须沿着一条线或在固定的表面上移动，那么系统的自由度则小于6。另一方面，如果一个系统带有可旋转或振动的扩展对象，那么它的自由度将大于6。

在经典力学中，任何给定时间下质点 Point particle的状态，通常是用拉格朗日形式 Lagrangian formalism 中的位置和速度坐标来描述，或者用哈密顿形式 Hamiltonian formalism 中的位置和动量坐标来描述。

在统计力学中，自由度指的是在描述某个系统的微观状态时，单个的标量数。[1]某个系统所有微观状态的规格参数都是该系统相空间中的一个点。

在化学的三维理想链 Ideal chain模型中，需要两个角度来描述每个单体 monomer 的方向。

指定二自由度通常很有用。因为它们有助于建立系统能量的二次函数。

气体分子

可视化双原子分子六个自由度的不同方式。（其中CM：系统的质心，T：平移运动，R：旋转运动，V：振动运动。）

在三维空间中，粒子的运动与它的三个自由度有关。双原子气体分子具有6个自由度。我们可以根据其分子的平动、转动和振动来分解这6个自由度。整个分子的质心运动具有三个自由度。除此之外，分子还有两个转动自由度和一个振动自由度。其中，这两个转动自由度，是在绕垂直于两个原子间直线的两个轴而发生的。但是，绕原子-原子键的转动并不是物理旋转。因此，在此种情况下，可以将双原子分子的自由度分解为：

[math]\displaystyle{ N = 6 = 3 + 2 + 1. }[/math]

对于一般的非线性分子，则需要考虑该分子的三个转动自由度，因此它的分解形式为：

[math]\displaystyle{ 3N = 3 + 3 + (3N - 6) }[/math]

这意味着当N>2时，N原子分子具有3N-6个振动自由度。不过在特殊情况下，例如一个吸附的大分子，转动自由度只能限制为一个。[2]

如上所述，还可以使用指定维度空间所需的最少坐标数来计算自由度。比如：

对于单个粒子，我们需要在二维平面中指定2个坐标，在三维空间中指定3个坐标。因此，它在三维空间中的自由度为3。

三维空间中，由2个粒子（例如双原子分子）组成且彼此之间具有恒定距离（假设d）的物体，（如下所示），可以表明其自由度为5。

假设这个物体中的一个粒子的坐标为(x1, y1, z1)，另一个粒子的坐标为(x2, y2, z2)，其中 z2未知。那么两个坐标之间距离的公式可以描述为：

[math]\displaystyle{ d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2} }[/math]

其等式含有一个未知数z2，不过我们可以对其求解。因此实际上是允许x1, x2, y1, y2, z1, 或者 z2其中之一是未知的。

与经典的能量均分定理 Equipartition theorem相反，在室温下，分子的振动对热容量 Heat capacity的贡献通常可忽略不计。这是因为这些自由度被冻结了，因为能量本征值之间的间隔超过了与环境温度（kBT）相对应的能量。在下表中，这些自由度均被忽略，因为它们对总能量的影响非常小。只有平移和旋转自由度对热容比 Heat capacity ratio有些许贡献（等量）。这就是为什么在室温下，单原子气体 γ=5/3和双原子气体 γ=7/5的原因。

不过，在非常高的温度下，差不多在振动温度(Θvib)的量级上，振动运动就不能被忽略了。

振动温度在103 K和104 K之间。[1]

单原子 线性分子 非线性分子
平移 (x, y, and z) 3 3 3
旋转 (x, y, and z) 0 2 3
总计 (不考虑室温下的振动) 3 5 6
振动 0 3N − 5 3N − 6
总计 (包括振动) 3 3N 3N

独立自由度

某个系统的自由度X1, ... , XN集合，如果集合的能量可以用以下形式表示，则它们是独立的：

[math]\displaystyle{ E = \sum_{i=1}^N E_i(X_i), }[/math]

其中Ei是唯一变量Xi的函数。

例如：如果X1 和 X2是两个自由度，并且E是关联的能量。

  • 如果[math]\displaystyle{ E = X_1^4 + X_2^4 }[/math]，则两个自由度是独立的。
  • 如果[math]\displaystyle{ E = X_1^4 + X_1 X_2 + X_2^4 }[/math]，则两个自由度不是独立的。其中X1和X2的乘积是描述两个自由度之间相互作用的耦合项。

这里的i值可以取1到N，第i个自由度Xi的值依据波尔兹曼分布 Boltzmann distribution 。其概率密度函数 Probability density function如下：

[math]\displaystyle{ p_i(X_i) = \frac{e^{-\frac{E_i}{k_B T}}}{\int dX_i \, e^{-\frac{E_i}{k_B T}}} }[/math],

在本节以及整篇文章中，方括号[math]\displaystyle{ \langle \rangle }[/math]表示其所包含数量的平均值。

系统的内能是每个自由度相关的平均能量之和：

[math]\displaystyle{ \langle E \rangle = \sum_{i=1}^N \langle E_i \rangle. }[/math]

二次自由度

如果与该自由度相关的能量项可以写成如下等式，则自由度Xi是二次的

[math]\displaystyle{ E = \alpha_i\,\,X_i^2 + \beta_i \,\, X_i Y }[/math],

其中Y是其他二次自由度的线性组合。

例如：如果X1 和 X2是两个自由度，而E是关联的能量：

  • 如果[math]\displaystyle{ E = X_1^4 + X_1^3 X_2 + X_2^4 }[/math]，则两个自由度既不是独立的也非二次的。
  • 如果[math]\displaystyle{ E = X_1^4 + X_2^4 }[/math]，则两个自由度是独立的但非二次的。
  • 如果[math]\displaystyle{ E = X_1^2 + X_1 X_2 + 2X_2^2 }[/math]，则两个自由度不是独立的，而是二次的。
  • 如果[math]\displaystyle{ E = X_1^2 + 2X_2^2 }[/math]，则两个自由度既是独立的并且是二次的。

例如，在牛顿力学中，一个二自由度的动力学系统是由一组具有恒定系数的齐次线性微分方程 homogeneous linear differential equations 控制的。

二次独立的自由度

如果能量与系统的微观状态有关，则X1, ... , XN是二次独立的自由度，它们可以写成：

[math]\displaystyle{ E = \sum_{i=1}^N \alpha_i X_i^2 }[/math]

能量均分定理

在统计力学的经典极限中，在热力学平衡 Thermodynamic equilibrium状态下，N个二次且独立自由度的系统内部能量为：

[math]\displaystyle{ U = \langle E \rangle = N\,\frac{k_B T}{2} }[/math]

此时，与自由度相关的平均能量为：

[math]\displaystyle{ \langle E_i \rangle = \int dX_i\,\,\alpha_i X_i^2\,\, p_i(X_i) = \frac{\int dX_i\,\,\alpha_i X_i^2\,\, e^{-\frac{\alpha_i X_i^2}{k_B T}}}{\int dX_i\,\, e^{-\frac{\alpha_i X_i^2}{k_B T}}} }[/math]
[math]\displaystyle{ \langle E_i \rangle = \frac{k_B T}{2}\frac{\int dx\,\,x^2\,\, e^{-\frac{x^2}{2}}}{\int dx\,\, e^{-\frac{x^2}{2}}} = \frac{k_B T}{2} }[/math]

由于自由度是独立的，因此系统的内部能量等于每个自由度带有的平均能量之和，由此得到了结果。

总结

尽管在数学上很方便，但将系统状态描述为相空间中的一个点，从根本上讲是不准确的。在量子力学中，体系运动状态的自由度被波函数的概念所取代，并且对应于其他自由度的算子 Operator具有离散的光谱。例如，电子或光子的本征角动量算符 Angular momentum operator （对应于转动自由度）只有两个特征值。当运动具有普朗克常数 Planck constant的量级时，这种离散变得非常明显，并且可以区分出各个自由度。

参考文献

  1. ↑ 1.0 1.1 Reif, F. (2009). Fundamentals of Statistical and Thermal Physics. Long Grove, IL: Waveland Press, Inc.. p. 51. ISBN 1-57766-612-7. 
  2. ↑ Waldmann, Thomas; Klein, Jens; Hoster, Harry E.; Behm, R. Jürgen (2013). "Stabilization of Large Adsorbates by Rotational Entropy: A Time-Resolved Variable-Temperature STM Study". ChemPhysChem. 14 (1): 162–9. doi:10.1002/cphc.201200531. PMID 23047526.

编者推荐

文章推荐

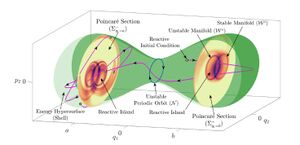
本文章进一步探讨了三个自由度时不相关哈密顿系统的反应岛理论的几何、解析和计算框架。在这种情况下，动力学发生在相空间的五维能量面中，并且由三维正常双曲不变球的四维稳定流形和不稳定流形控制。稳定流形和不稳定流形具有球标的几何结构，对此本文章提供了研究这些球标及其交点决定轨迹动态演化的方法。这种几何图像是通过拉格朗日描述子的计算技术实现的。在一组轨迹中，拉格朗日描述符允许被识别最接近稳定或不稳定流形的轨迹。利用截面上流形的近似，能够计算能量面两个区域之间的通量。
Reactive Islands for Three Degrees-of-Freedom Hamiltonian Systems
能量均分定理是经典统计力学非常重要的结论,本文章介绍了能量均分定理的推导以及运用范围。

视频推荐

气体的热运动量与组成气体的分子结构有关，除了单原子分子可看作质点（只有平动）外，一般由于两个原子以上组成的分子不仅有平动，而且还有转动和分子内原子间的振动，其相应能量不能忽略。为此，需要引用力学中关于自由度的概念来描述分子结构。

课程推荐

本课程讲解了具有一个自由度的机械系统以及关于非线性中心的理论。具体讲解了具有一个自由度的机械系统、双井中的粒子、对称、同宿轨道、能量面、关于非线性中心的定理、钟摆以及圆柱相空间的概念及原理、应用等。

本中文词条由Sizuka和Jie参与编译，Vicky和SyouTK编辑，欢迎在讨论页面留言。

本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

取自“https://wiki.swarma.org/index.php?title=自由度&oldid=25575”