自由能原理
自由能原理 Free energy principle是一个正式的陈述,它解释了生物系统和非生物系统如何通过将自己限制在有限的几个状态而保持在非平衡稳态。[1]它表明系统最小化了内部状态的自由能函数,而内部状态包含了对环境中隐藏状态的信任。自由能的内隐最小化在形式上与变分贝叶斯方法 Variational Bayesian methods有关,最初由Karl Friston引入,作为神经科学中对具身知觉的解释,[2]在那里它也被称为“主动推理”。
自由能原理解释了一个给定系统的存在,它通过一个马尔可夫毯 Markov blanket建模,试图最小化他们的世界模型和他们的感觉和相关知觉之间的差异。这种差异可以被描述为”出其不意” ,并通过不断修正系统的世界模型来减少这种差异。因此,这个原理是基于贝叶斯的观点,即大脑是一个“推理机”。弗里斯顿为最小化增加了第二条路线: 行动。通过积极地将世界改变为预期的状态,系统也可以使系统的自由能最小化。弗里斯顿认为这是所有生物反应的原理。[3]弗里斯顿还认为,他的原则即适用于精神障碍也适用于人工智能。基于主动推理原则的人工智能实现比其他方法显示出优势。[3]关于这一原则的讨论也受到批评,认为它引用的形而上学假设与可检验的科学预测相去甚远,使这一原则不可证伪。在2018年的一次采访中,弗里斯顿承认,自由能原理不能被恰当地证伪: “自由能原理就是它的本来面目——一个原理。就像汉密尔顿的静止作用原理一样,它不能被证伪。这是不能被推翻的。事实上,除非你问可衡量的系统是否符合这一原则,否则你用它做不了什么。”
自由能原理被批评为很难理解,甚至对专家来说也是如此。[4]对这一原则的讨论也被批评为援引了形而上学远离可检验的科学预测的假设,使这一原则成为不可证伪的。[5]在2018年的一次采访中,弗里斯顿承认自由能原则并不恰当可证伪性:“自由能原则就是它的本来面目-一个原则。与哈密顿定常作用原理一样,它是不可证伪的。这是无法反驳的。事实上,除非你问可测量系统是否符合这一原则,否则你对此无能为力。”[6]
背景
自我组织的生物系统——比如细胞或大脑——可以被理解为最小化变分自由能的概念,是基于亥姆霍兹在无意识推理[7]以及随后的心理学[8]和机器学习[9]治疗方面的工作。变分自由能是观测值及其隐含原因的概率密度的函数。这个变分密度的定义关系到一个概率模型,从假设的原因产生预测观测。在这种情况下,自由能提供了一个近似贝叶斯模型[10]的证据。因此,它的最小化可以被看作是一个贝叶斯推断过程。当一个系统积极地进行观测以最小化自由能时,它隐含地进行了积极推理并最大化其世界模型的证据。
然而,自由能也是结果自信息的一个上限,长期的平均值是熵。这意味着,如果一个系统采取行动来最小化自由能,它将隐含地放置一个熵的结果-或感官状态-它的样本上限。[11][12]
与其他理论的关系
主动推理与良好的调节器定理以及自组织的相关理论,如自组装、模式形成、自创生和拓扑实践密切相关。它涉及控制论、协同学和具身认知理论中所考虑的主题。由于自由能可以用变分密度下观测值的期望能量减去其熵来表示,因此它也与最大熵原理有关。最后,由于能量的时间平均值是作用量,因此最小变分自由能原理是最小作用量原理。
主动推理与好调节器定理密切相关[13]以及与自组织的内容相关,[14][15] 例如自组装,模式形成,自生[16]和实践[17].
它解决了控制论,协同学中考虑的主题[18]以及具身认知。由于自由能可以表示为变分密度下观测值的期望能量减去其熵,因此它也与最大熵原理有关。[19] 最后,由于能量的时间平均是作用量,最小变分自由能原理是一种最小作用原理。
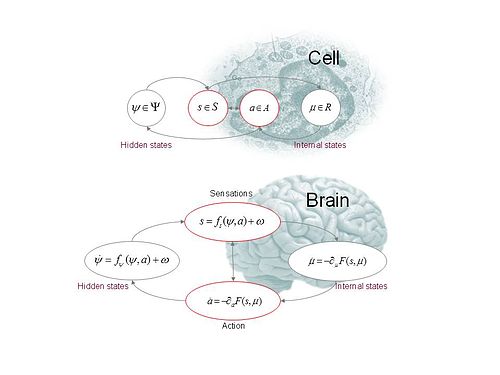
这些示意图说明了如何将状态划分为内部状态和隐藏状态或外部状态,这些状态由一个马尔可夫毯(包括感觉状态和活动状态)分隔开来。下面的面板显示了这个分区,因为它将应用于大脑中的动作和感知;活动和内部状态将感官状态的自由能功能最小化。随后内部状态的自组织与感知相对应,而动作将大脑状态与外部状态耦合。上面的面板显示完全相同的依赖性,但重新排列,使内部状态与细胞内状态相关联,而感觉状态成为细胞膜的表面状态覆盖活性状态(例如,细胞骨架的肌动蛋白丝)。
定义
定义(连续公式):主动推理依赖于元组[math]\displaystyle{ (\Omega,\Psi,S,A,R,q,p) }[/math] ,
- “一个样本空间”[math]\displaystyle{ \Omega }[/math]–从中提取随机波动[math]\displaystyle{ \Omega\in\Omega }[/math]
- “隐藏或外部状态”[math]\displaystyle{ \Psi:\Psi\times A\times\Omega\to\mathbb{R} }[/math]——引起感觉状态并依赖于动作
- “感觉状态”[math]\displaystyle{ S:\Psi\times A\times\Omega\to\mathbb{R} }[/math]——动作和隐藏状态的概率映射
- “动作”[math]\displaystyle{ A:S\times R \to \mathbb{R} }[/math]——这取决于感觉和内部状态
- “内部状态”[math]\displaystyle{ R:R\times S\to\mathbb{R} }[/math]——引起动作并依赖于感觉状态
- “生成密度”[math]\displaystyle{ p(s, \psi \mid m) }[/math]——在生成模型下的感觉和隐藏状态
- “变分密度”[math]\displaystyle{ q(\psi \mid \mu) }[/math]–由R中的内部状态[math]\displaystyle{ \mu \in R }[/math]参数化的隐藏状态[math]\displaystyle{ \psi \in \Psi }[/math]
其目的是最大限度地提高模型的证据,或者最大限度地减少惊喜。这通常涉及隐状态的棘手边缘化,因此用变分自由能上界代替惊奇。这个公式建立在一个马尔可夫毯子(包括行动和感官状态) ,分离内部和外部状态。如果内部状态和作用力使自由能最小化,那么它们在感觉状态的熵上设置了一个上限
行动与感知
目标是最大化模型证据[math]\displaystyle{ p(s\mid m) }[/math]或最小化意外[math]\displaystyle{ -\log p(s\mid m) }[/math]。这通常涉及隐藏态的难以处理的边缘化,因此意外被一个较高的变分自由能边界所取代。[9]然而,这意味着内部状态也必须最小化自由能,因为自由能是感官和内部状态的函数:
- [math]\displaystyle{ a(t) = \underset{a}{\operatorname{arg\,min}} \{ F(s(t),\mu(t)) \} }[/math]
- [math]\displaystyle{ \mu(t) = \underset{\mu}{\operatorname{arg\,min}} \{ F(s(t),\mu)) \} }[/math]
- [math]\displaystyle{ \underset{\mathrm{free-energy}} {\underbrace{F(s,\mu)}} = \underset{\mathrm{energy}} {\underbrace{ E_q[-\log p(s,\psi \mid m)]}} - \underset{\mathrm{entropy}} {\underbrace{ H[q(\psi \mid \mu)]}} = \underset{\mathrm{surprise}} {\underbrace{ -\log p(s \mid m)}} + \underset{\mathrm{divergence}} {\underbrace{ D_{\mathrm{KL}}[q(\psi \mid \mu) \parallel p(\psi \mid s,m)]}} \geq \underset{\mathrm{surprise}} {\underbrace{ -\log p(s \mid m)}} }[/math]
这导致了一个双重最小化的行动和内部状态,分别对应于行动和感知。
自由能最小化
自由能最小化和自组织
变分自由能是一种信息论泛函,不同于热力学(亥姆霍兹)自由能。然而,变分自由能的复杂性项与亥姆霍兹自由能具有相同的固定点(假设系统是热力学闭合的,而不是孤立的)。这是因为如果感觉干扰暂停(适当长的时间) ,复杂性是最小的(因为准确性可以忽略)。在这一点上,系统处于平衡状态,内部状态通过最小能量原理使亥姆霍兹自由能最小。
自由能最小化被认为是自组织系统的一个标志。[20] 这个公式建立在一个马尔可夫毯(包括行动和感觉状态)分离内部和外部状态。如果内部状态和行为使自由能最小化,那么它们就给感官状态的熵设置了一个上限。
- [math]\displaystyle{ \lim_{T\to\infty} \frac{1}{T} \underset{\text{free-action}} {\underbrace{\int_0^T F(s(t),\mu (t))\,dt}} \ge \lim_{T\to\infty} \frac{1}{T} \int_0^T \underset{\text{surprise}}{\underbrace{-\log p(s(t)\mid m)}} \, dt = H[p(s\mid m)] }[/math]
自由能最小化相当于最大化感观状态和内部状态之间的互信息,使变分密度参数化(对于固定熵变分密度)。利用信息论描述最优行为的相关处理。
这是因为在遍历假设下,惊喜的长期平均值是熵。这个界限抵抗了一种自然的无序倾向,这种无序倾向与热力学第二定律和涨落定理有关。
自由能最小化与贝叶斯推理
自由能最小化为在不确定性条件下建立神经元推理和学习的规范(贝叶斯最优)模型提供了一种有用的方法,因此符合贝叶斯脑假设。由自由能最小化描述的神经元过程取决于隐藏状态的性质:[math]\displaystyle{ \Psi = X \times \Theta \times \Pi }[/math],它可以包括时间相关变量、时不变参数和随机波动的精度(逆方差或温度)。最小化变量、参数和精度分别对应于推理、学习和不确定性编码。
所有的贝叶斯推断都可以用自由能最小化来表示,例如,[21]当自由能相对于内部态最小化时,隐态上变分密度和后验密度之间的Kullback–Leibler散度最小化。当变分密度的形式固定时,这对应于近似的贝叶斯推理,否则对应于精确的贝叶斯推理。因此,自由能最小化提供了贝叶斯推理和滤波的一般描述(例如,卡尔曼滤波)。它也用于贝叶斯模型选择,其中自由能可以有效地分解为复杂性和准确性:
- [math]\displaystyle{ \underset{\text{free-energy}} {\underbrace{ F(s,\mu)}} = \underset{\text{complexity}} {\underbrace{ D_\mathrm{KL}[q(\psi\mid\mu)\parallel p(\psi\mid m)]}} - \underset{\mathrm{accuracy}} {\underbrace{E_q[\log p(s\mid\psi,m)]}} }[/math]
自由能最小化使知觉中的无意识推理的概念正规化
具有最小自由能的模型提供了数据的精确解释,降低了复杂性成本(参见奥卡姆剃刀和计算成本的更正式的处理方法[22])。这里,复杂性是变分密度和关于隐藏状态的先验信念(即用于解释数据的有效自由度)之间的差异。
自由能最小化与热力学
变分自由能是一种信息论泛函,不同于热力学Helmholtz自由能。[23]然而,变分自由能的复杂性项与Helmholtz自由能具有相同的不动点(假设系统是热力学封闭而非孤立的)。这是因为如果感官干扰被暂停(一段适当长的时间),复杂性被最小化(因为准确度可以忽略)。此时,系统处于平衡状态,内部状态根据最小能量原理[24]使亥姆霍兹自由能最小化。
自由能最小化与信息论
自由能最小化相当于最大化感官状态和内部状态之间的互信息,使变分密度参数化(对于固定熵变分密度)[11]这将自由能最小化与最小冗余原则联系起来。[25]并且联系到用信息论描述最优行为的相关处理[26][27]
神经科学中的自由能最小化
自由能最小化为在不确定性条件下建立神经元推理和学习的规范(Bayes最优)模型提供了一种有效的方法[28] 因此符合贝叶斯脑假说[29]。由自由能最小化描述的神经元过程取决于隐藏状态的性质:[math]\displaystyle{ \Psi=X\times\Theta\times\Pi }[/math],它可以包括时间相关变量、时不变参数和随机波动的精度(逆方差或温度)。最小化变量、参数和精度分别对应于推理、学习和不确定性编码。
感性推理与分类
自由能最小化使知觉中的无意识推理概念正式化[7][9]并提供了神经元处理的规范(贝叶斯)理论。神经元动力学的相关过程理论是基于通过梯度下降最小化自由能。这对应于广义贝叶斯滤波(其中~表示广义运动坐标中的变量,[math]\displaystyle{ D }[/math]是一个导数矩阵运算符):[30]
- [math]\displaystyle{ \dot{\tilde{\mu}} = D \tilde{\mu} - \partial_{\mu}F(s,\mu)\Big|_{\mu = \tilde{\mu}} }[/math]
通常,定义自由能的生成模型是非线性和层次结构的(就像大脑中的皮层层次结构)。广义滤波的特殊情况包括卡尔曼滤波,它在形式上等价于[预测编码]][31] 一种关于大脑中信息传递的流行隐喻。在分层模型下,预测编码涉及到上升(自下而上)预测错误和下降(自上而下)预测的循环交换[32]这与感觉器官的解剖学和生理学[33]以及动力系统[34]是一致的。
知觉学习与记忆
在预测编码中,通过自由能(自由作用)时间积分的梯度上升来优化模型参数会降低到联想或 Hebbian可塑性,并与大脑中的synaptic可塑性相关。
知觉的精确性、注意力和显著性
优化精度参数对应于优化预测误差的增益(参见Kalman增益)。在预测性编码的神经元似是而非的实现中,[32]这对应于优化浅表锥体细胞的兴奋性,并被解释为注意增益。[35]
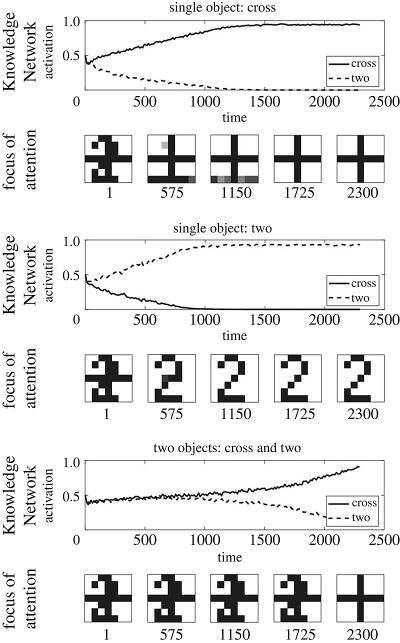
关于自上而下与自下而上的争论,已经被作为一个主要的开放性问题的注意,一个计算模型已经成功地说明了自上而下和自下而上机制之间的往复循环性质。利用已建立的注意涌现模型SAIM,作者提出了一个称为PE-SAIM的模型,与标准模型相比,该模型从自上而下的立场接近选择性注意。该模型考虑了发送到同一级别或更高级别的转发预测误差,以最小化表示数据及其原因之间的差异的能量函数,换句话说,生成模型和后验模型之间的差异。为了提高有效性,他们还在模型中加入了刺激物之间的神经竞争。该模型的一个显著特点是仅根据任务执行过程中的预测误差来重新构造自由能函数。
- [math]\displaystyle{ \dfrac{\partial E^{total}(Y^{VP},X^{SN},x^{CN},y^{KN})}{\partial y^{SN}_{mn}}=x^{CN}_{mn}-b^{CN}\varepsilon^{CN}_{nm}+b^{CN}\sum_{k}(\varepsilon^{KN}_{knm}) }[/math]
其中,[math]\displaystyle{ E^{total} }[/math]是神经网络的总能量函数,[math]\displaystyle{ \varepsilon^{KN}_{knm} }[/math]是生成模型(先验)和后验随时间变化的预测误差。[36])
比较这两个模型的结果发现他们的结果之间有显著的相似性,同时指出了一个显著的差异,即在SAIM的标准版本中,模型的重点主要是兴奋性连接,而在PE-SAIM中,抑制性连接将被用来进行推断。该模型对人体实验的脑电和功能磁共振数据具有较高的预测精度。该模型还被证明适合以高精度预测从人体实验中提取的 EEG 和 fMRI 数据。同样,Yahya 等人。还应用自由能原理提出了一个主要依赖于 SAIM 的隐性选择性视觉注意中的模板匹配计算模型。[37]根据这项研究,通过在原始神经网络中插入自上而下的信号来达到整个状态空间的总自由能,由此我们推导出一个包含前馈和后向预测误差的动力学系统。
主动推理
当梯度下降应用于动作[math]\displaystyle{ \dot{a} = -\partial_aF(s,\tilde{\mu}) }[/math]时,运动控制可以理解为通过下降(皮质脊髓)预测参与的经典反射弧。这提供了一种形式主义,将平衡点解推广到自由度问题[38]移动轨迹。
主动推理与最优控制
主动推理与最优控制有关,它用状态转移或流的先验信念替换价值或成本函数。[39]这充分利用了贝叶斯滤波和Bellman方程解之间的紧密联系。然而,主动推理从状态空间的标量[math]\displaystyle{ V(x) }[/math]和向量[math]\displaystyle{ W(x) }[/math]值函数(c.f.,Helmholtz分解)指定的流[math]\displaystyle{ f=\Gamma\cdot\nabla V+\nabla\times W }[/math]开始。这里,[math]\displaystyle{ \Gamma }[/math]是随机波动的幅度,成本是[math]\displaystyle{ c(x)=f\cdot\nabla V+\nabla\cdot\Gamma\cdot V }[/math]。流上的先验[math]\displaystyle{ p(\tilde{x}\mid m) }[/math]诱导了一个先验的超状态[math]\displaystyle{ p(x\mid m)=\exp(V(x)) }[/math]这是相应的正向Kolmogorov方程的解。[40]相反,在假设<math>W=0的情况下,最优控制优化了给定成本函数的流量(即,流量没有旋度或具有详细平衡)。通常,这需要向后求解Kolmogorov方程。[41]
主动推理与最优决策(博弈)理论
最优决策问题(通常表示为部分可观测马尔可夫决策过程)通过将效用函数吸收到先验信念中,在主动推理中处理。在此设置中,具有高效用(低成本)的状态是代理希望占用的状态。通过给生成模型配备模型控制的隐藏状态,最小化可变自由能的策略(控制序列)会导致高效用状态。 [42]
神经生物学上,神经调节剂多巴胺被认为通过调节编码预测误差的主细胞的增益来报告预测误差的准确性。[43] 这与多巴胺在报告预测错误“本身”中的作用密切相关,但在形式上与之不同[44]以及与计算账户相关[45]
主动推理与认知神经科学
主动推理已被用于解决认知神经科学、脑功能和神经精神病学的一系列问题,包括:行动观察,[46]镜像神经元,[47] 扫视和视觉搜索,[48][49] 眼球运动,[50] 睡眠,[51]幻觉,[52] 注意,[35] 动作选择,[43] 意识,[53][54] hysteria[55] 还有精神病。[56] 对主动推理中行为的解释常常依赖于这样一种观点,即大脑有“顽固的预测”,它无法更新,从而导致使这些预测成真的行为。[57]
参考文献
- ↑ Ashby, W. R. (1962). Principles of the self-organizing system.in Principles of Self-Organization: Transactions of the University of Illinois Symposium, H. Von Foerster and G. W. Zopf, Jr. (eds.), Pergamon Press: London, UK, pp. 255–278.
- ↑ Friston, Karl; Kilner, James; Harrison, Lee (2006). "A free energy principle for the brain" (PDF). Journal of Physiology-Paris. Elsevier BV. 100 (1–3): 70–87. doi:10.1016/j.jphysparis.2006.10.001. ISSN 0928-4257. PMID 17097864.
- ↑ 3.0 3.1 Shaun Raviv: The Genius Neuroscientist Who Might Hold the Key to True AI. In: Wired, 13. November 2018
- ↑ Freed, Peter (2010). "Research Digest". Neuropsychoanalysis. Informa UK Limited. 12 (1): 103–106. doi:10.1080/15294145.2010.10773634. ISSN 1529-4145.
- ↑ Colombo, Matteo; Wright, Cory (2018-09-10). "First principles in the life sciences: the free-energy principle, organicism, and mechanism". Synthese. Springer Science and Business Media LLC. doi:10.1007/s11229-018-01932-w. ISSN 0039-7857.
- ↑ Friston, Karl (2018). "Of woodlice and men: A Bayesian account of cognition, life and consciousness. An interview with Karl Friston (by Martin Fortier & Daniel Friedman)". ALIUS Bulletin. 2: 17–43.
- ↑ 7.0 7.1 Helmholtz, H. (1866/1962). Concerning the perceptions in general. In Treatise on physiological optics (J. Southall, Trans., 3rd ed., Vol. III). New York: Dover.
- ↑ Gregory, R. L. (1980-07-08). "Perceptions as hypotheses". Philosophical Transactions of the Royal Society of London. B, Biological Sciences. The Royal Society. 290 (1038): 181–197. Bibcode:1980RSPTB.290..181G. doi:10.1098/rstb.1980.0090. ISSN 0080-4622. JSTOR 2395424. PMID 6106237.
- ↑ 9.0 9.1 9.2 Dayan, Peter; Hinton, Geoffrey E.; Neal, Radford M.; Zemel, Richard S. (1995). "The Helmholtz Machine" (PDF). Neural Computation. MIT Press - Journals. 7 (5): 889–904. doi:10.1162/neco.1995.7.5.889. ISSN 0899-7667. PMID 7584891.
- ↑ Beal, M. J. (2003). Variational Algorithms for Approximate Bayesian Inference. Ph.D. Thesis, University College London.
- ↑ 11.0 11.1 Karl, Friston (2012-10-31). "A Free Energy Principle for Biological Systems" (PDF). Entropy. MDPI AG. 14 (11): 2100–2121. Bibcode:2012Entrp..14.2100K. doi:10.3390/e14112100. ISSN 1099-4300. PMC 3510653. PMID 23204829.
- ↑ Colombo, Matteo; Wright, Cory (2018-09-10). "First principles in the life sciences: the free-energy principle, organicism, and mechanism". Synthese. Springer Science and Business Media LLC. doi:10.1007/s11229-018-01932-w. ISSN 0039-7857.
- ↑ Conant, R. C., & Ashby, R. W. (1970). Every Good Regulator of a system must be a model of that system. Int. J. Systems Sci. , 1 (2), 89–97.
- ↑ Kauffman, S. (1993). The Origins of Order: Self-Organization and Selection in Evolution. Oxford: Oxford University Press.
- ↑ Nicolis, G., & Prigogine, I. (1977). Self-organization in non-equilibrium systems. New York: John Wiley.
- ↑ Maturana, H. R., & Varela, F. (1980). Autopoiesis: the organization of the living. In V. F. Maturana HR (Ed.), Autopoiesis and Cognition. Dordrecht, Netherlands: Reidel.
- ↑ Nikolić, D. (2015). Practopoiesis: Or how life fosters a mind. Journal of theoretical biology, 373, 40-61.
- ↑ Haken, H. (1983). Synergetics: An introduction. Non-equilibrium phase transition and self-organisation in physics, chemistry and biology (3rd ed.). Berlin: Springer Verlag.
- ↑ Jaynes, E. T. (1957). Information Theory and Statistical Mechanics. Physical Review Series II, 106 (4), 620–30.
- ↑ Crauel, H., & Flandoli, F. (1994). Attractors for random dynamical systems. Probab Theory Relat Fields, 100, 365–393.
- ↑ Roweis, S., & Ghahramani, Z. (1999). A unifying review of linear Gaussian models. Neural Computat. , 11 (2), 305–45. doi:10.1162/089976699300016674
- ↑ Ortega, P. A., & Braun, D. A. (2012). Thermodynamics as a theory of decision-making with information processing costs. Proceedings of the Royal Society A, vol. 469, no. 2153 (20120683) .
- ↑ Evans, D. J. (2003). A non-equilibrium free energy theorem for deterministic systems. Molecular Physics , 101, 15551–4.
- ↑ Jarzynski, C. (1997). Nonequilibrium equality for free energy differences. Phys. Rev. Lett., 78, 2690.
- ↑ Barlow, H. (1961). Possible principles underlying the transformations of sensory messages In W. Rosenblith (Ed.), Sensory Communication (pp. 217-34). Cambridge, MA: MIT Press.
- ↑ Linsker, R. (1990).Perceptual neural organization: some approaches based on network models and information theory. Annu Rev Neurosci. , 13, 257–81.
- ↑ Bialek, W., Nemenman, I., & Tishby, N. (2001). Predictability, complexity, and learning. Neural Computat., 13 (11), 2409–63.
- ↑ Friston, K. (2010). The free-energy principle: a unified brain theory? Nat Rev Neurosci. , 11 (2), 127–38.
- ↑ Knill, D. C., & Pouget, A. (2004). The Bayesian brain: the role of uncertainty in neural coding and computation. Trends Neurosci. , 27 (12), 712–9.
- ↑ Friston, K., Stephan, K., Li, B., & Daunizeau, J. (2010). Generalised Filtering. Mathematical Problems in Engineering, vol., 2010, 621670
- ↑ Rao, R. P., & Ballard, D. H. (1999). Predictive coding in the visual cortex: a functional interpretation of some extra-classical receptive-field effects. Nat Neurosci. , 2 (1), 79–87.
- ↑ 32.0 32.1 Mumford, D. (1992). On the computational architecture of the neocortex. II. Biol. Cybern. , 66, 241–51.
- ↑ Bastos, A. M., Usrey, W. M., Adams, R. A., Mangun, G. R., Fries, P., & Friston, K. J. (2012). Canonical microcircuits for predictive coding. Neuron , 76 (4), 695–711.
- ↑ Adams, R. A., Shipp, S., & Friston, K. J. (2013). Predictions not commands: active inference in the motor system. Brain Struct Funct. , 218 (3), 611–43
- ↑ 35.0 35.1 Feldman, H., & Friston, K. J. (2010). Attention, uncertainty, and free-energy. Frontiers in Human Neuroscience, 4, 215.
- ↑ Abadi K.A., Yahya K., Amini M., Heinke D. & Friston, K. J. (2019). Excitatory versus inhibitory feedback in Bayesian formulations of scene construction. 16 R. Soc. Interface
- ↑ Yahya K., Fard P.R., & Friston, K.J. (2014). [DOI: 10.1007/s10339-013-0597-6 A free energy approach to visual attention: a connectionist model]. Cogn Process (2014) 15:107.
- ↑ Feldman, A. G., & Levin, M. F. (1995). The origin and use of positional frames of reference in motor control. Behav Brain Sci. , 18, 723–806.
- ↑ Friston, K., (2011). What is optimal about motor control?. Neuron, 72(3), 488–98.
- ↑ Friston, K., & Ao, P. (2012). Free-energy, value and attractors. Computational and mathematical methods in medicine, 2012, 937860.
- ↑ Kappen, H., (2005). Path integrals and symmetry breaking for optimal control theory. Journal of Statistical Mechanics: Theory and Experiment, 11, p. P11011.
- ↑ Friston, K., Samothrakis, S. & Montague, R., (2012). Active inference and agency: optimal control without cost functions. Biol. Cybernetics, 106(8–9), 523–41.
- ↑ 43.0 43.1 Friston, K. J. Shiner T, FitzGerald T, Galea JM, Adams R, Brown H, Dolan RJ, Moran R, Stephan KE, Bestmann S. (2012). Dopamine, affordance and active inference. PLoS Comput. Biol., 8(1), p. e1002327.
- ↑ Fiorillo, C. D., Tobler, P. N. & Schultz, W., (2003). Discrete coding of reward probability and uncertainty by dopamine neurons. Science, 299(5614), 1898–902.
- ↑ Frank, M. J., (2005). Dynamic dopamine modulation in the basal ganglia: a neurocomputational account of cognitive deficits in medicated and nonmedicated Parkinsonism. J Cogn Neurosci., Jan, 1, 51–72.
- ↑ Friston, K., Mattout, J. & Kilner, J., (2011). Action understanding and active inference. Biol Cybern., 104, 137–160.
- ↑ Kilner, J. M., Friston, K. J. & Frith, C. D., (2007). Predictive coding: an account of the mirror neuron system. Cogn Process., 8(3), pp. 159–66.
- ↑ Friston, K., Adams, R. A., Perrinet, L. & Breakspear, M., (2012). Perceptions as hypotheses: saccades as experiments. Front Psychol., 3, 151.
- ↑ Mirza, M., Adams, R., Mathys, C., Friston, K. (2018). Human visual exploration reduces uncertainty about the sensed world. PLoS One, 13(1): e0190429
- ↑ Perrinet L, Adams R, Friston, K. Active inference, eye movements and oculomotor delays. Biological Cybernetics, 108(6):777-801, 2014.
- ↑ Hobson, J. A. & Friston, K. J., (2012). Waking and dreaming consciousness: Neurobiological and functional considerations. Prog Neurobiol, 98(1), pp. 82–98.
- ↑ Brown, H., & Friston, K. J. (2012). Free-energy and illusions: the cornsweet effect. Front Psychol , 3, 43.
- ↑ Rudrauf, David; Bennequin, Daniel; Granic, Isabela; Landini, Gregory; Friston, Karl; Williford, Kenneth (2017-09-07). "A mathematical model of embodied consciousness" (PDF). Journal of Theoretical Biology. 428: 106–131. doi:10.1016/j.jtbi.2017.05.032. ISSN 0022-5193. PMID 28554611.
- ↑ K, Williford; D, Bennequin; K, Friston; D, Rudrauf (2018-12-17). "The Projective Consciousness Model and Phenomenal Selfhood". Frontiers in Psychology (in English). 9: 2571. doi:10.3389/fpsyg.2018.02571. PMC 6304424. PMID 30618988.
- ↑ Edwards, M. J., Adams, R. A., Brown, H., Pareés, I., & Friston, K. J. (2012). A Bayesian account of 'hysteria'. Brain , 135(Pt 11):3495–512.
- ↑ Adams RA, Perrinet LU, Friston K. (2012). Smooth pursuit and visual occlusion: active inference and oculomotor control in schizophrenia. PLoS One. , 12;7(10):e47502
- ↑ Yon, Daniel; Lange, Floris P. de; Press, Clare (2019-01-01). "The Predictive Brain as a Stubborn Scientist". Trends in Cognitive Sciences (in English). 23 (1): 6–8. doi:10.1016/j.tics.2018.10.003. ISSN 1364-6613. PMID 30429054.
编者推荐
集智课程
临界现象的标度性与超标度关系
本课程中,将从自由能的奇异部分的齐次性,推出临界现象的标度性与超标度关系。
知乎文章
本条目由水流心不竞翻译,Evangeline审校,薄荷编辑,如有问题,欢迎在讨论页面进行讨论。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。