蒙特卡罗模拟
蒙特卡罗方法 Monte Carlo methods,或称蒙特卡罗实验 Monte Carlo experiments,是一大类计算算法的集合,依靠重复的随机抽样来获得数值结果。基本概念是利用随机性来解决理论上可能是确定性的问题。这类方法通常用于解决物理和数学问题,当面对棘手问题而束手无策时,往往它们可以大显身手。蒙特卡罗方法主要用于解决3类问题:[1]最优化,数值积分,依据概率分布生成图像。
在物理学相关问题中,蒙特卡罗方法可用于模拟具有多个耦合自由度的系统,如流体、无序材料、强耦合固体和细胞结构(参见细胞波茨模型 Cellular Potts Model、相互作用粒子系统 Interacting Particle Systems、麦肯-弗拉索夫过程 McKean-Vlasov Processes、气体动力学模型 Kinetic Models of Gases)。
其他例子包括:对输入中具有重大不确定性的现象进行建模,如商业中的风险计算,以及在数学中对具有复杂边界条件的多维定积分进行评估。在系统工程问题(空间、石油勘探、飞机设计等)的应用中,基于蒙特卡罗的故障预测、成本超支和进度超支通常比人类的直觉或其他的“软性”方法更有效。[2]
理论上,蒙特卡罗方法可以用来解决任何具有概率解释的问题。根据大数定律 Law of Large Numbers,用某个随机变量的期望值描述的积分可以用该变量独立样本的经验均值(即样本均值)来近似。当变量的概率分布被参数化时,数学家们经常使用马尔可夫链蒙特卡罗 Markov chain Monte Carlo(MCMC)采样器。[3][4][5]其中心思想是设计一个具有给定稳态概率分布 Stationary Probability Distribution的有效马尔可夫链模型。也就是说,在极限情况下,马尔科夫链蒙特卡洛方法生成的样本将成为来自期望(目标)分布的样本。[6][7] 通过遍历定理 Ergodic Theorem,稳态分布可以用马尔科夫链蒙特卡洛采样器随机状态的经验测度来近似。
在其他问题中,要实现的目标则是从满足非线性演化方程的概率分布序列中生成图像。这些概率分布流总是可以解释为马尔可夫过程 Markov process的随机状态的分布,其转移概率依赖于当前随机状态的分布(见麦肯-弗拉索夫过程,非线性滤波方程 Nonlinear Filtering Equation)。[8][9]其他情况下,我们给出了采样复杂度不断增加的概率分布流(如时间范围不断增加的路径空间模型,与温度参数降低有联系的玻尔兹曼—吉布斯测度 Boltzmann-Gibbs Measures,以及许多其他例子)。这些模型也可以看作是一个非线性马尔可夫链的随机状态规律的演化。[9][10]模拟这些复杂非线性马尔可夫过程的一个自然的方法是对过程的多个副本进行抽样,用抽样的经验测度替代演化方程中未知的随机状态分布。与传统的蒙特卡罗和马尔科夫链蒙特卡洛方法相比,这些平均场粒子 Mean Field Particle技术依赖于连续相互作用的样本。平均场一词反映了每个样本(也就是粒子、个体、步行者、媒介、生物或表现型)与过程的经验测量相互作用的事实。当系统大小趋近于无穷时,这些随机经验测度收敛于非线性马尔可夫链随机状态的确定性分布,从而使粒子之间的统计相互作用消失。
尽管其概念和算法简单,但与蒙特卡罗模拟相关的计算成本却是高的惊人。一般情况下,该方法需要大量的样本来获得良好的近似,如果单个样本的处理时间较长,可能会导致总运行时间长度难以控制。[11]尽管在非常复杂的问题中,这是一个严重的限制,但该算法令人尴尬的并行性质允许通过本地处理器、集群、云计算、GPU、FPGA等的并行计算策略来降低高昂的成本(或许降低到可以接受的水平上)。[12][13][14][15]
概述
蒙特卡罗方法各不相同,但趋于遵循一个特定的模式:
1、定义可能输入的域
2、从域上的概率分布随机生成输入
3、对输入进行确定性计算
4、汇总结果
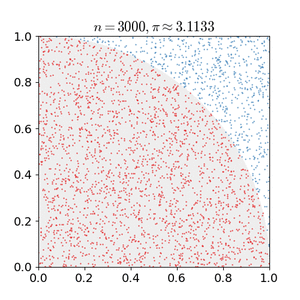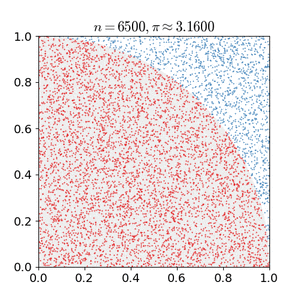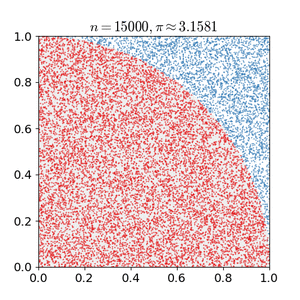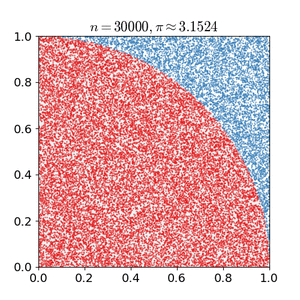
例如,考虑一个单位正方形内嵌的四分之一圆。考虑到它们的面积比是π/4,π的值可以用蒙特卡罗方法来近似:[16]
1、画一个正方形,然后在其中划出一个四分之一圆
2、在正方形上均匀散布给定数量的点
3、计算四分之一圆内的点数,即满足距离原点小于1的
4、四分之一圆内部计数与总样本计数之比是两个区域之比的估计值,π/4。把结果乘以4就可以估算出π的值。
在这个过程中,输入域是限定四分之一圆的正方形。我们通过将颗粒散射到正方形上来产生随机输入,然后对每个输入执行计算(测试它是否在四分之一圆内)。汇总这些结果会产生最终的结果——π的近似值。
有两个重要的考虑因素:
1、如果这些点不是均匀分布的,那么近似效果就会很差。
2、这一过程需要很多点。如果整个正方形中只有几个点是随机放置的,那么这个近似值通常是很差的。平均而言,随着放置更多的点,近似值精度会提升。
应用蒙特卡罗方法需要大量的随机数,这也就刺激了伪随机数生成器 Pseudorandom Number Generators的发展,伪随机数生成器比以前用于统计抽样的随机数表要快得多。
历史
在开发蒙特卡罗方法之前,人们模拟测试一个已经解决的确定性问题,通过统计抽样估计模拟中的不确定性。蒙特卡罗模拟将这种方法反转,使用概率元启发式方法Probabilistic Metaheuristics解决确定性问题(参见模拟退火法 Simulated Annealing)。
蒙特卡罗方法的早期变种被设计来解决 布丰投针 Buffon's Needle Problem问题,在布丰投针问题中,π可以通过将针落在由平行等距条组成的地板上来估计。20世纪30年代,恩里科·费米 Enrico Fermi在研究中子扩散时首次尝试了蒙特卡罗方法,但他没有发表这项工作。[17]
20世纪40年代末,斯坦尼斯拉夫·乌拉姆 Stanislaw Ulam在洛斯阿拉莫斯国家实验室研究核武器项目时,发明了现代版的马尔可夫链蒙特卡罗方法。在乌拉姆的突破之后,约翰·冯·诺伊曼 John von Neumann立即意识到了它的重要性。冯·诺伊曼为ENIAC(人类第一台电子数字积分计算机)编写了程序来进行蒙特卡罗计算。1946年,洛斯阿拉莫斯的核武器物理学家正在研究中子在可裂变材料中的扩散。[17]尽管拥有大部分必要的数据,例如中子在与原子核碰撞之前在物质中的平均运行距离,以及碰撞后中子可能释放出多少能量,但洛斯阿拉莫斯的物理学家们无法用传统的、确定性的数学方法解决这个问题。此时乌拉姆建议使用随机实验。他后来回忆当初灵感产生过程:
我最初构想和尝试蒙特卡洛法是在1946年,当时我正从疾病中康复,时常玩单人纸牌游戏。那时我会思考这样一个问题:一盘52张的加菲尔德纸牌成功出牌的几率有多大?在花了大量时间尝试通过纯粹的组合计算来估计它们之后,我想知道是否有一种比“抽象思维”更实际的方法,可能不是将它展开100次,然后简单地观察和计算成功的游戏数量。在快速计算机新时代开始时,这已经是可以想象的了,我立刻想到了中子扩散和其他数学物理的问题,以及更一般的情形—如何将由某些微分方程描述的过程转换成可解释为一系列随机操作的等价形式。后来(1946年),我向约翰·冯·诺伊曼描述了这个想法,然后我们开始计划实际的计算。[18]
冯·诺依曼和乌拉姆的工作是秘密进行的,需要一个代号。[19] 冯·诺依曼和乌拉姆的一位同事,尼古拉斯·梅特罗波利斯 Nicholas Metropolis建议使用蒙特卡洛这个名字,这个名字指的是摩纳哥的蒙特卡洛赌场,乌拉姆的叔叔会和亲戚借钱然后去那里赌博。[17]使用“真正随机”的随机数列表是非常慢的,然而冯·诺依曼使用平方取中法 Middle-Square Method开发了一种计算伪随机数生成器的方法。虽然许多人一直批评这种方法较为粗糙原始,但是冯·诺依曼也意识到这一点:他证明这种方法比任何其他方法都快,并指出当它出错时,人们可以轻易发现,不像其他方法产生的错误可能会不易察觉。[20]
尽管受到当时的计算工具严重限制,蒙特卡洛方法依然是曼哈顿计划 Manhattan Project所需模拟的核心关键。20世纪50年代,它们在洛斯阿拉莫斯用于与氢弹开发有关的早期工作,并在物理学、物理化学和运筹学领域得到普及。兰德公司 Rand Corporation和美国空军是当时负责资助和宣传蒙特卡罗方法信息的两个主要组织,从那时起他们开始在许多不同的领域广泛地应用这一方法。
更复杂的平均场型粒子蒙特卡罗方法的理论产生于20世纪60年代中期,最初来自于小亨利·麦基恩 Henry P. McKean Jr.研究流体力学中出现的一类非线性抛物型偏微分方程的马尔可夫解释。[21][22] 西奥多·爱德华·哈里斯 Theodore E. Harris和赫曼·卡恩 Herman Kahn在1951年发表了一篇开创性文章,使用平均场遗传型蒙特卡罗方法来估计粒子传输能量。[23] 这一方法在演化计算中也被用作启发式自然搜索算法(又称元启发式)。这些平均场计算技术的起源可以追溯到1950年和1954年,当时阿兰·图灵 Alan Turing在基因类型突变-选择学习机器上的工作,[24]以及来自新泽西州普林斯顿高等研究院的尼尔斯·阿尔·巴里里利 Nils Aall Barricelli的文章。[25][26]
量子蒙特卡罗方法,更具体地说,扩散蒙特卡罗方法也可以解释为费曼-卡茨路径积分 Feynman–Kac Path Integrals的平均场粒子蒙特卡罗近似。[27][28][29][30][31][32][33] 量子蒙特卡罗方法的起源通常归功于恩里科·费米 Enrico Fermi和罗伯特·里希特迈耶 Robert Richtmyer于1948年开发了中子链式反应的平均场粒子解释,[34]但是用于估计量子系统的基态能量(在简化矩阵模型中)的第一个类启发式和遗传型粒子算法(也称为重取样或重构蒙特卡洛方法)则是由杰克·H·海瑟林顿在1984年[33] 提出。在分子化学中,使用遗传类启发式的粒子方法(又名删减和富集策略)可以追溯到1955年——马歇尔·罗森布鲁斯 Marshall Rosenbluth和阿里安娜·罗森布鲁斯Arianna Rosenbluth的开创性工作。[35]
在高级信号处理和贝叶斯推断 Bayesian Inference中使用序列蒙特卡罗方法 Sequential Monte Carlo是最近才出现的。1993年,高登等人在他们的开创性工作中发表了蒙特卡罗重采样算法在贝叶斯推论统计学中的首次应用。[36]作者将他们的算法命名为“自举过滤器”,并证明了与其他过滤方法相比,他们的自举过滤算法不需要任何关于系统状态空间或噪声的假设。此外北川源四郎也进行了“蒙特卡洛过滤器”相关的开创性研究。[37]在1990年代中期,皮埃尔·德尔·莫勒尔 Pierre Del Moral [38]和希米尔康·卡瓦略 Himilcon Carvalho以及皮埃尔·德尔·莫勒尔、安德烈·莫宁 André Monin和杰拉德·萨鲁特 Gérard Salut [39]发表了关于粒子过滤器的文章。1989-1992年间,在LAAS-CNRS(系统分析和体系结构实验室),皮埃尔·德尔·莫勒尔、J·C·诺亚 J. C. Noyer、G·里加尔 G. Rigal和杰拉德·萨鲁特开发了粒子滤波器用于信号处理。他们与STCAN(海军建造和武装服务技术部)、IT公司DIGILOG共同完成了一系列关于雷达/声纳和GPS信号处理问题的限制性和机密性研究报告。[40][41][42][43][44][45]这些序列蒙特卡罗方法可以解释为一个接受拒绝采样器配备了相互作用的回收机制。
从1950年到1996年,所有关于顺序蒙特卡罗方法的出版物,包括计算物理和分子化学中引入的删减和重采样蒙特卡罗方法,目前应用于不同的情况的自然和类启发式算法,没有任何一致性证明,也没有讨论估计的偏差和基于谱系和遗传树的算法。皮埃尔·德尔·莫勒尔在1996年的写作中阐述了关于这些粒子算法的数学基础,并对其第一次进行了严格的分析。[38][46]
20世纪90年代末,丹·克里桑 Dan Crisan、杰西卡·盖恩斯 Jessica Gaines和特里·利昂斯 Terry Lyons,[47][48][49] 以及丹·克里桑、皮埃尔·德尔·莫勒尔和特里·利昂斯也发展了具有不同种群大小的分支型粒子方法。[50] 2000年,皮埃尔·德尔·莫勒尔、爱丽丝·吉奥内 A. Guionnet和洛朗·米克洛 L. Miclo进一步发展了这一领域。[28][51][52]
定义
对于如何定义蒙特卡洛还没有达成共识。例如,里普利 Ripley [53]将大多数概率建模定义为随机模拟 stochastic simulation,蒙特卡罗则包含蒙特卡罗积分和蒙特卡罗统计检验。萨维罗斯基 Sawilowsky[54]区分了模拟、蒙特卡罗方法和蒙特卡罗模拟:模拟是对现实的一种虚构的表现,蒙特卡罗方法是一种可以用来解决数学或统计问题的技术,蒙特卡罗模拟使用重复抽样来获得某些现象(或行为)的统计特性。例如:
- 模拟:从区间[0,1]中绘制一个伪随机均匀变量可以用来模拟抛硬币:如果值小于或等于0.50,则结果为正面,但如果值大于0.50,则结果为反面。这是一个模拟,但不是蒙特卡洛模拟。
- 蒙特卡洛方法:将一盒硬币倒在桌子上,然后计算正面与反面落地的硬币比例。这是一种确定重复掷硬币行为的蒙特卡洛方法,但它不是模拟。
- 蒙特卡罗模拟法:一次或多次从区间[0,1]中绘制“大量”伪随机均匀变量,赋值小于或等于0.50作为正面,大于0.50为反面。这是一个多次掷硬币的“蒙特卡罗模拟”行为。
卡洛斯 Kalos和惠特洛克 Whitlock[55]指出,这几种方法的区别并不总是容易分辨。例如,来自原子的辐射是一种自然的随机过程。它可以直接模拟,也可以用随机方程描述其平均行为,这些随机方程本身可以用蒙特卡罗方法求解。“实际上,同样的计算机代码可以同时被看作是‘自然模拟’或者通过自然抽样解方程。”
蒙特卡罗和随机数 Monte Carlo and random numbers 这种方法的主要思想是基于重复随机抽样和统计分析来计算结果。蒙特卡洛模拟实际上是一种随机实验,在这种情况下,这些实验的结果并不为人所知。蒙特卡罗模拟的典型特征是有许多未知参数,其中许多参数很难通过实验获得。[56] 蒙特卡罗模拟方法并不总是要求真正的随机数是有用的(尽管对于一些应用程序,如质数测试,不可预测性是至关重要的)。[57] 许多最有用的技术是使用确定性的伪随机序列,使测试和重新运行模拟变得很容易。伪随机序列在某种意义上表现地“足够随机”,这是进行良好模拟唯一必需的性质。
所谓“足够随机”的含义一般取决于应用场景,但通常也应该通过一系列统计测试。当需要考虑的序列中元素足够多时,检验这些数是均匀分布的,还是遵循另一个期望的分布是最简单常见的方法之一。连续样本之间的弱相关性通常也是可取的,或必要的。
萨维罗斯基列出了高质量蒙特卡罗模拟的特点:[54]
- (伪随机数)生成器具有某些特征(例如,序列重复之前有一个很长的“周期”)
- (伪随机数)生成器可以产生能通过随机性测试的值
- 有足够的样本来确保准确的结果
- 使用适当的取样方法
- 使用的算法对建模内容是有效的
- 它可以对问题中的现象进行模拟
伪随机数采样算法 Pseudo-random Number Sampling Algorithms是将均匀分布的伪随机数转化为按给定概率分布分布的数。
低差异序列 Low-discrepancy sequences通常被用来代替空间中的随机采样,因为它们确保了均匀的覆盖,并且通常比使用随机或伪随机序列的蒙特卡罗模拟具有更快的收敛顺序。基于它们的使用的方法称为准蒙特卡罗方法 Quasi-Monte Carlo Methods。
为了评估随机数质量对蒙特卡罗模拟结果的影响,天体物理学研究人员测试了通过英特尔的RDRAND指令集生成的加密安全伪随机数,并将其与梅森旋转算法 Mersenne Twister生成的伪随机数进行了比较,在蒙特卡洛模拟褐矮星射电耀斑的过程中。RDRAND是最接近真实随机数生成器的伪随机数生成器。对于生成107个随机数的试验,典型伪随机数生成器生成的模型与RDRAND之间没有统计差异。[58]
蒙特卡罗模拟与“假设”情景
使用概率的方法不一定都是蒙特卡洛模拟——例如,使用单点估计的确定性建模。模型中的每个不确定变量都被赋予一个“最佳猜测”估计。为每个输入变量选择场景(如最佳、最差或最可能的情况)并记录结果。[59]
相比之下,蒙特卡罗模拟从概率分布中抽取每个变量的样本,产生数百或数千个可能的结果。对结果进行分析,得到不同结果发生的概率。[60] 例如,对使用传统”假设”情景运行的电子表格成本构造模型进行比较,然后再与蒙特卡罗模拟和三角概率分布进行比较,结果表明蒙特卡罗分析的范围比”假设”分析的范围窄。这是因为“假设”分析对所有情景给予了同等的权重(见量化公司融资的不确定性),而蒙特卡罗方法几乎不在非常低的概率区域抽样。这部分样本被称为“稀有事件”。
应用
蒙特卡罗方法尤其适用于模拟输入和多自由度耦合系统中具有明显不确定性的现象。应用领域包括:
物理科学
蒙特卡罗方法在计算物理、物理化学及相关应用领域中非常重要,从复杂的量子色动力学 Quantum Chromodynamics计算到设计热屏蔽 Heat Shields和气动形式,以及在辐射剂量计算中模拟辐射传输等方面有广泛应用。[61][62][63]在统计物理中,蒙特卡罗分子建模 Monte Carlo molecular Modeling是计算分子动力学的替代方法,蒙特卡罗方法用于计算简单粒子和聚合物体系的统计场理论。[35][64] 量子蒙特卡罗方法解决了量子系统的多体问题 Many-Body Problem。[8][9][27] 在辐射材料科学 Radiation Materials Science中,模拟离子注入的二元碰撞近似通常是基于蒙特卡罗方法来选择下一个碰撞原子。[65] 在实验粒子物理学中,蒙特卡罗方法用于设计探测器,了解它们的行为,并将实验数据与理论进行比较。在天体物理学中,它们被以不同的方式用于模拟星系演化[66]和微波辐射通过粗糙行星表面的传输。[67]蒙特卡罗方法也用于构成现代天气预报基础的集合模型。
工程学
蒙特卡罗方法被广泛应用于工程设计中的敏感度分析和工艺设计中的定量概率分析。这种需求来源于典型过程模拟的交互性、共线性和非线性行为。比如说:
- 在微电子工程 Microelectronics Engineering中,蒙特卡罗方法被用于分析模拟和数字集成电路中相关和不相关的变化。
- 在地质统计学 Geostatistics和地质冶金学 Geometallurgy中,蒙特卡罗方法是矿物处理流程设计的基础,并有助于定量风险分析。[68]
- 在风能产量分析中,考虑不同的不确定性(P90、P50等),计算风电场在其生命周期内的预测发电量。
- 在流体动力学,特别是稀薄气体动力学 Rarefied Gas Dynamics中,采用直接模拟蒙特卡罗方法 Direct Simulation Monte Carlo[71]结合高效计算算法求解有限努森数 Knudsen Number流体的玻尔兹曼方程。[72]
- 在自主机器人中,蒙特卡洛定位 Monte Carlo Localization可以确定机器人的位置。它通常应用于随机滤波器,如卡尔曼滤波器 Kalman Filter或粒子滤波器 Particle Filter,构成同步定位和映射算法 Simultaneous Localization and Mapping(SLAM)的核心。
- 在电信行业,在规划无线网络时,必须证明设计适用于各种不同用户数量、用户位置和他们想使用的服务的场景。蒙特卡罗方法通常用于生成这些用户及其状态。然后对网络性能进行评估,如果结果不能令人满意,则进行网络设计优化。
- 在可靠性工程中,给定部件级响应,蒙特卡罗仿真用来计算系统级响应。例如,对于一个受地震事件影响的交通网络,给定其组件,如桥梁、道路等的失效概率,蒙特卡洛模拟可以用来评估网络的k-终端可靠性。[73][74][75]另一个意义深远的例子是应用蒙特卡罗方法求解广义更新过程 Generalized Renewal Process的G-更新方程。[76]
- 在信号处理和贝叶斯推断中,粒子滤波器和序列蒙特卡罗技术是一类平均场粒子方法,用于对给定噪声和局部观测的信号过程进行采样和计算后验分布,使用相互作用的经验测度。
- 在地下水模拟中,利用蒙特卡罗方法产生了大量的非均质参数场实现,用于模型不确定性量化或参数反演。[77]
C气候变化与辐射强迫
政府间气候变化专门委员会采用蒙特卡罗方法对辐射强迫进行概率密度函数分析。
基于总温室气体、气溶胶强迫和总人为强迫的有效辐射强迫 Effective Radiative Forcing(ERF)概率密度函数 Probability Density Function(PDF)。温室气体由充分混合温室气体 Well Mixed Greenhouse Gases(WMGHG)、臭氧和平流层水蒸汽组成。概率密度函数是根据表8.6提供的不确定性生成的。基于鲍彻 Boucher和海伍德 Haywood(2001)的方法,通过蒙特卡洛模拟,将单个辐射强迫介质组合起来,得出工业时代的总强迫。来自地面反照率变化和混合尾迹和尾迹诱导的卷云的有效辐射强迫的概率密度函数包含在总人为强迫中,而不是单独显示为独立的概率密度函数。我们目前还没有有效辐射强迫来估计一些强迫机制,例如:臭氧、土地利用、太阳能等。[78]
计算生物学
蒙特卡罗方法被用于计算生物学 Computational Biology的各个领域,例如在系统发育学中的贝叶斯推断,或者用于研究生物系统,例如基因组、蛋白质[79]或膜[80]。该系统可以在粗粒度或从头计算框架中研究,这取决于所需的准确性。计算机模拟使我们能够监测特定分子的局部环境,看看是否正在发生某种化学反应,例如。在无法进行物理实验的情况下,可以进行思维实验(例如:断键,在特定位置引入杂质,改变局部/整体结构,或引入外部场)。
计算机图形学
路径追踪 Path Tracing偶尔称为蒙特卡罗光线追踪,通过随机追踪可能的光路样本来呈现一个三维场景。对任何给定像素的重复采样最终将导致样本的平均值收敛到渲染方程的正确解,使其成为现存物理上最精确的三维图形渲染方法之一。
应用统计学
蒙特卡罗方法的统计标准是由萨维罗斯基制定的。 [81]在应用统计学中,蒙特卡罗方法至少可用于四种目的:
1、比较在现实数据条件下小样本的竞争统计。虽然根据经典理论分布(例如,正态曲线,柯西分布 Cauchy distribution)数据的渐近条件(即,无限大的样本量和无限小的处理效果),i型误差和统计的幂次特性可以进行计算,但是实际数据往往没有这样的分布。[82]
2、提供比精确检验更有效的假设检验的实现,例如排列检验(通常无法计算),同时比渐近分布的临界值更精确。
3、提供一份来自后验概率贝叶斯推断的随机样本。然后基于这个样本进行近似和总结后验的所有基本特征。
4、提供负对数似然函数的海赛矩阵的有效随机估计,这些估计的平均值可以形成费雪信息量 Fisher Information矩阵的估计。[83][84]
蒙特卡罗方法也是近似随机和排列检验之间的折衷。近似随机化测试是基于所有排列的特定子集(这可能需要大量的内务处理,其中的排列经过充分考虑)。蒙特卡罗方法是基于指定数量的随机排列(如果一个排列被绘制两次或更频繁,则在精度上有较小的损失,因为不必跟踪哪些排列已经被选择)。
人工智能在游戏中的应用
蒙特卡罗方法已经发展成为一种称作蒙特卡洛树搜索 Monte-Carlo tree search的技术,它可以用来搜索游戏中的最佳移动。可能的移动被组织在一个搜索树和许多随机模拟被用来估计每个移动的长期潜力。一个黑盒模拟器代表对手的动作。[85]
蒙特卡罗树搜索(MCTS)方法有四个步骤:[86]
1、从树的根节点开始,选择最佳的子节点,直到达到叶节点。
2、展开叶节点并选择其中一个子节点。
3、以该节点开始玩一个模拟游戏。
4、使用模拟游戏的结果来更新节点及其祖先。
在许多模拟游戏过程中,净效应是代表移动的一个节点将上升或下降的值,希望与该节点移动的结果(无论好坏)相对应。
蒙特卡洛树搜索已成功地用于游戏,如围棋[87],彩虹棋[88],海战棋[89],《三宝棋》[90]和印度斗兽棋[91]。
设计与视觉效果
蒙特卡罗方法在求解辐射场和能量传输耦合积分微分方程方面也很有效,因此这些方法已用于全局光照计算,生成逼真的虚拟三维模型图像,并应用于电子游戏、建筑、设计、计算机生成电影、以及电影特效。[92]
搜寻与救援
美国海岸警卫队在其计算机建模软件——搜救最优规划系统 Search and Rescue Optimal Planning System (SAROPS)中使用蒙特卡罗方法,以便在搜索和救援行动中计算可能的船只位置。每个模拟可以生成多达一万个数据点,这些数据点是根据提供的变量随机分布的。[93]然后根据这些数据推断生成搜索模式,以优化包容概率(POC)和检测概率(POD),这两者合起来等于总体成功概率(POS)。最终,作为概率分布的一个实际应用,以最迅速和最便捷的救援方法,拯救生命和资源。[94]
金融与商业
蒙特卡罗模拟通常用于评估影响不同决策方案结果的风险和不确定性。蒙特卡洛模拟允许业务风险分析师纳入不确定性变量的总体影响,如销售额、商品和劳动力价格、利率和汇率,以及不同风险事件的影响,如合同的取消或税法的改变。
在金融领域中,蒙特卡罗方法经常被用于评估业务单位或公司层面的项目投资,或其他金融估值。它们可以用来模拟项目进度,其中模拟汇总了对最坏情况、最好情况和每个任务最可能持续时间的估计,以确定整个项目的结果[1]蒙特卡罗方法也用于期权定价,违约风险分析。[95][96][97]此外,它们还可以用来估计医疗干预的财务影响。[98]
法律
蒙特卡洛方法曾用来评估一项提案的潜在价值,这项提案旨在帮助威斯康星州的女性请愿者成功申请骚扰和家庭虐待限制令。通过帮助妇女完成请愿,向她们提供更多的宣传,从而有可能减少强奸和人身攻击的风险。然而,还有许多变量无法完全估计,包括限制令的有效性,上访者的成功率,以及许多其他因素。该研究通过试验来改变这些变量,从而对整个计划的成功程度进行总体估计。[99]
数学应用
一般来说,蒙特卡罗方法在数学中通过产生合适的随机数(也见随机数产生)和观察符合某些性质的数字分数来解决各种问题。对于过于复杂而无法用解析方法求解的问题,这种方法是有用的。蒙特卡罗方法最常见的应用是蒙特卡罗积分。
积分
蒙特卡罗积分是通过比较随机点和函数值来工作的。
确定性数值积分算法在低维运行良好,但在函数具有多个变量时会遇到两个问题。首先,随着维数的增加,需要进行的功能评估数量迅速增加。例如,如果10个评估在一个维度上提供了足够的精确度,那么100个维度需要10100 点,这太多了以至于无法计算。这就是所谓的维数灾难 Curse of Dimensionality。其次,多维区域的边界可能非常复杂,因此将问题简化为迭代积分可能是不可行的。[100]100维问题是很常见的的,因为在许多物理问题中,一个“维度”等同于一个自由度。
蒙特卡罗方法提供了一种方法来摆脱这种指数增长的计算时间。只要所涉及的函数具有合理的性质,就可以在100维空间中随机选取一些点,并在这些点上取某种函数值的平均值来估计。通过中心极限定理 Central Limit Theorem,这个方法显示 [math]\displaystyle{ \scriptstyle 1/\sqrt{N} }[/math] 收敛,即,不管维数多少,将采样点的数目翻两番,误差则会减半。[100]
这种方法改进,在统计学中称为重要性抽样,涉及随机抽样点,但更频繁地在被积函数较大的地方进行。要精确地做到这一点,必须已知积分,或者也可以用一个类似函数的积分来近似这个积分,或者使用自适应例程,如分层抽样 Stratified Sampling,递归分层抽样 Recursive Stratified Sampling,自适应伞抽样 Adaptive Umbrella Sampling[101][102] 或VEGAS算法 VEGAS Algorithm。
一个类似的方法——拟蒙特卡罗方法,使用低差异序列。这些序列能更好地“填充”区域,更频繁地采样最重要的点,因此拟蒙特卡罗方法往往能更快地收敛于积分。
另一类在体积中的取样点方法是模拟在它上面的随机行走(马尔可夫链蒙特卡罗)。这些方法包括 梅特罗波利斯-黑斯廷斯算法 Metropolis-Hastings Algorithm、吉布斯取样法 Gibbs Sampling、王-兰道算法 Wang and Landau Algorithm,以及交互型马尔可夫链蒙特卡罗方法,如顺序蒙特卡罗采样法。[103]
模拟与优化
随机数在数值模拟中的另一个强大和非常流行的应用是数值优化。问题是最小化(或最大化)某些向量的函数,这些向量通常有多个维度。许多问题都可以用这种方式表述: 例如,一个计算机国际象棋程序可以视为试图找到一组,比如说,在最后产生最佳评估函数的10步棋。在旅行推销员问题中,目标是最小化旅行距离。也有应用于工程设计,如多学科设计优化 Multi-disciplinary Design Optimization (MDO)。它也已应用于准一维模型,以解决粒子动力学问题,有效地探索大型位形空间。参考文献[104]是对许多与模拟和优化有关的问题的全面回顾。
旅行推销员问题被称为传统的最优化问题问题。也就是说,确定最佳路径所需的所有事实(每个目的地之间的距离)都是确定无疑的,目标是通过可能的旅行选择得出总距离最小的路径。然而假设我们不想最小化访问每个想要的目的地所需的总距离,而是想最小化到达每个目的地所需的总时间。这超越了传统的优化,因为旅行时间是固有的不确定性(交通堵塞,一天的时间,等)。因此,为了确定我们的最佳路径,我们需要使用模拟优化来首先了解从一个点到另一个点可能需要的时间范围(在这个例子中用概率分布代表,而不是特定的距离),然后优化我们的旅行决策,以确定最佳路径遵循考虑到这种不确定性。
逆问题
逆问题的概率公式引出了模型空间中概率分布的定义。这种概率分布结合了先验信息和通过测量一些可观测参数(数据)获得的新信息。由于在一般情况下,将数据与模型参数联系起来的理论是非线性的,模型空间中的后验概率可能不容易描述(可能是多模态的,有些矩可能没有定义等)。
在分析逆问题时,获得最大似然模型通常是不够的,因为我们通常还希望得到数据分辨率的信息。在一般情况下,我们可能有许多模型参数,而对边际概率密度的检验可能是不切实际的,甚至是无用的。但可以根据后验概率分布伪随机地生成大量模型,并以传递模型属性的相对可能性信息的方式对模型进行分析和显示。这可以通过一种有效的蒙特卡罗方法来完成,即使在没有先验分布的显式公式可用的情况下。
最著名的重要抽样方法梅特罗波利斯-黑斯廷斯算法可以推广使用,它提供了一种允许分析(可能是高度非线性的)具有复杂先验信息和任意噪声分布数据的逆问题的方法。[105][106]
哲学
麦克拉肯 McCracken对蒙特卡罗方法进行了广泛的阐述。[107]利沙科夫 Elishakoff、[108]格林尼·雅诺夫 Grüne-Yanoff和魏里希 Weurich讨论了方法的一般哲学[109]。
参见
- Auxiliary field Monte Carlo
- Biology Monte Carlo method
- Comparison of risk analysis Microsoft Excel add-ins
- Direct simulation Monte Carlo
- Dynamic Monte Carlo method
- Genetic algorithms
- Kinetic Monte Carlo
- List of software for Monte Carlo molecular modeling
- Mean field particle methods
- Monte Carlo method for photon transport
- Monte Carlo methods for electron transport
- Morris method
- Multilevel Monte Carlo method
- Particle filter
- Quasi-Monte Carlo method
- Sobol sequence
- Temporal difference learning
参考文献
引文
- ↑ Kroese, D. P.; Brereton, T.; Taimre, T.; Botev, Z. I. (2014). "Why the Monte Carlo method is so important today". WIREs Comput Stat. 6 (6): 386–392. doi:10.1002/wics.1314.
- ↑ Hubbard, Douglas; Samuelson, Douglas A. (October 2009). "Modeling Without Measurements". OR/MS Today: 28–33.
- ↑ Metropolis, Nicholas; Rosenbluth, Arianna W.; Rosenbluth, Marshall N.; Teller, Augusta H.; Teller, Edward (1953-06-01). "Equation of State Calculations by Fast Computing Machines". The Journal of Chemical Physics. 21 (6): 1087–1092. Bibcode:1953JChPh..21.1087M. doi:10.1063/1.1699114. ISSN 0021-9606.
- ↑ Hastings, W. K. (1970-04-01). "Monte Carlo sampling methods using Markov chains and their applications". Biometrika. 57 (1): 97–109. Bibcode:1970Bimka..57...97H. doi:10.1093/biomet/57.1.97. ISSN 0006-3444.
- ↑ Liu, Jun S.; Liang, Faming; Wong, Wing Hung (2000-03-01). "The Multiple-Try Method and Local Optimization in Metropolis Sampling". Journal of the American Statistical Association. 95 (449): 121–134. doi:10.1080/01621459.2000.10473908. ISSN 0162-1459.
- ↑ Spall, J. C. (2003). "Estimation via Markov Chain Monte Carlo". IEEE Control Systems Magazine. 23 (2): 34–45. doi:10.1109/MCS.2003.1188770.
- ↑ Hill, Stacy D.; Spall, James C. (2019). "Stationarity and Convergence of the Metropolis-Hastings Algorithm: Insights into Theoretical Aspects". IEEE Control Systems Magazine. 39: 56–67. doi:10.1109/MCS.2018.2876959.
- ↑ 8.0 8.1 Kolokoltsov, Vassili (2010). Nonlinear Markov processes. Cambridge Univ. Press. pp. 375.
- ↑ 9.0 9.1 9.2 Del Moral, Pierre (2013). Mean field simulation for Monte Carlo integration. Chapman & Hall/CRC Press. pp. 626. http://www.crcpress.com/product/isbn/9781466504059. "Monographs on Statistics & Applied Probability"
- ↑ Del Moral, P; Doucet, A; Jasra, A (2006). "Sequential Monte Carlo samplers". Journal of the Royal Statistical Society, Series B. 68 (3): 411–436. arXiv:cond-mat/0212648. doi:10.1111/j.1467-9868.2006.00553.x.
- ↑ Shonkwiler, R. W.; Mendivil, F. (2009). Explorations in Monte Carlo Methods. Springer.
- ↑ Atanassova, E.; Gurov, T.; Karaivanova, A.; Ivanovska, S.; Durchova, M.; Dimitrov, D. (2016). "On the parallelization approaches for Intel MIC architecture". AIP Conference Proceedings. 1773: 070001. doi:10.1063/1.4964983.
- ↑ Cunha Jr, A.; Nasser, R.; Sampaio, R.; Lopes, H.; Breitman, K. (2014). "Uncertainty quantification through the Monte Carlo method in a cloud computing setting". Computer Physics Communications. 185(5): 1355–1363. doi:10.1016/j.cpc.2014.01.006.
- ↑ Wei, J.; Kruis, F.E. (2013). "A GPU-based parallelized Monte-Carlo method for particle coagulation using an acceptance–rejection strategy". Chemical Engineering Science. 104: 451–459. doi:10.1016/j.ces.2013.08.008.
- ↑ Lin, Y.; Wang, F.; Liu, B. (2018). "Random number generators for large-scale parallel Monte Carlo simulations on FPGA". Journal of Computational Physics. 360: 93–103. doi:10.1016/j.jcp.2018.01.029.
- ↑ Kalos, Malvin H.; Whitlock, Paula A. (2008). Monte Carlo Methods. Wiley-VCH. ISBN 978-3-527-40760-6.
- ↑ 17.0 17.1 17.2 Metropolis, N. (1987). "The beginning of the Monte Carlo method" (PDF). Los Alamos Science (1987 Special Issue dedicated to Stanislaw Ulam): 125–130.
- ↑ Eckhardt, Roger (1987). "Stan Ulam, John von Neumann, and the Monte Carlo method" (PDF). Los Alamos Science (15): 131–137.
- ↑ Mazhdrakov, Metodi; Benov, Dobriyan; Valkanov, Nikolai (2018). The Monte Carlo Method. Engineering Applications. ACMO Academic Press. p. 250. ISBN 978-619-90684-3-4.
- ↑ Peragine, Michael (2013). The Universal Mind: The Evolution of Machine Intelligence and Human Psychology. Xiphias Press. Retrieved 2018-12-17.
- ↑ McKean, Henry, P. (1967). "Propagation of chaos for a class of non-linear parabolic equations". Lecture Series in Differential Equations, Catholic Univ. 7: 41–57.
- ↑ McKean, Henry, P. (1966). "A class of Markov processes associated with nonlinear parabolic equations". Proc. Natl. Acad. Sci. USA. 56 (6): 1907–1911. Bibcode:1966PNAS...56.1907M. doi:10.1073/pnas.56.6.1907. PMC 220210. PMID 16591437.
- ↑ Herman, Kahn; Theodore, Harris E. (1951). "Estimation of particle transmission by random sampling" (PDF). Natl. Bur. Stand. Appl. Math. Ser. 12: 27–30.
- ↑ Turing, Alan M. (1950). "Computing machinery and intelligence". Mind. LIX (238): 433–460. doi:10.1093/mind/LIX.236.433.
- ↑ Barricelli, Nils Aall (1954). "Esempi numerici di processi di evoluzione". Methodos: 45–68.
- ↑ Barricelli, Nils Aall (1957). "Symbiogenetic evolution processes realized by artificial methods". Methodos: 143–182.
- ↑ 27.0 27.1 Del Moral, Pierre (2004). Feynman–Kac formulae. Genealogical and interacting particle approximations. Probability and Its Applications. Springer. p. 575. ISBN 9780387202686. https://www.springer.com/mathematics/probability/book/978-0-387-20268-6. "Series: Probability and Applications"
- ↑ 28.0 28.1 Del Moral, P.; Miclo, L. (2000). "Branching and interacting particle systems approximations of Feynman–Kac formulae with applications to non-linear filtering". Séminaire de Probabilités, XXXIV. Lecture Notes in Mathematics. 1729. Berlin: Springer. pp. 1–145. doi:10.1007/BFb0103798. ISBN 978-3-540-67314-9. MR 1768060.}}
- ↑ Del Moral, Pierre; Miclo, Laurent (2000). "A Moran particle system approximation of Feynman–Kac formulae". Stochastic Processes and Their Applications. 86 (2): 193–216. doi:10.1016/S0304-4149(99)00094-0.
- ↑ Del Moral, Pierre (2003). "Particle approximations of Lyapunov exponents connected to Schrödinger operators and Feynman–Kac semigroups". ESAIM Probability & Statistics. 7: 171–208. doi:10.1051/ps:2003001.
- ↑ Assaraf, Roland; Caffarel, Michel; Khelif, Anatole (2000). "Diffusion Monte Carlo Methods with a fixed number of walkers" (PDF). Phys. Rev. E. 61 (4): 4566–4575. Bibcode:2000PhRvE..61.4566A. doi:10.1103/physreve.61.4566. PMID 11088257. Archived from the original (PDF) on 2014-11-07.
- ↑ Caffarel, Michel; Ceperley, David; Kalos, Malvin (1993). "Comment on Feynman–Kac Path-Integral Calculation of the Ground-State Energies of Atoms". Phys. Rev. Lett. 71 (13): 2159. Bibcode:1993PhRvL..71.2159C. doi:10.1103/physrevlett.71.2159. PMID 10054598.
- ↑ 33.0 33.1 Hetherington, Jack, H. (1984). "Observations on the statistical iteration of matrices". Phys. Rev. A. 30 (2713): 2713–2719. Bibcode:1984PhRvA..30.2713H. doi:10.1103/PhysRevA.30.2713.
- ↑ Fermi, Enrique; Richtmyer, Robert, D. (1948). "Note on census-taking in Monte Carlo calculations" (PDF). LAM. 805 (A).
Declassified report Los Alamos Archive
- ↑ 35.0 35.1 Rosenbluth, Marshall, N.; Rosenbluth, Arianna, W. (1955). "Monte-Carlo calculations of the average extension of macromolecular chains". J. Chem. Phys. 23 (2): 356–359. Bibcode:1955JChPh..23..356R. doi:10.1063/1.1741967. S2CID 89611599.
- ↑ Gordon, N.J.; Salmond, D.J.; Smith, A.F.M. (April 1993). "Novel approach to nonlinear/non-Gaussian Bayesian state estimation". IEE Proceedings F - Radar and Signal Processing. 140 (2): 107–113. doi:10.1049/ip-f-2.1993.0015. ISSN 0956-375X. S2CID 12644877.
- ↑ Kitagawa, G. (1996). "Monte carlo filter and smoother for non-Gaussian nonlinear state space models". Journal of Computational and Graphical Statistics. 5 (1): 1–25. doi:10.2307/1390750. JSTOR 1390750.
- ↑ 38.0 38.1 Del Moral, Pierre (1996). "Non Linear Filtering: Interacting Particle Solution" (PDF). Markov Processes and Related Fields. 2 (4): 555–580.
- ↑ Carvalho, Himilcon; Del Moral, Pierre; Monin, André; Salut, Gérard (July 1997). "Optimal Non-linear Filtering in GPS/INS Integration" (PDF). IEEE Transactions on Aerospace and Electronic Systems. 33 (3): 835. Bibcode:1997ITAES..33..835C. doi:10.1109/7.599254. S2CID 27966240.
- ↑ P. Del Moral, G. Rigal, and G. Salut. "Estimation and nonlinear optimal control: An unified framework for particle solutions". LAAS-CNRS, Toulouse, Research Report no. 91137, DRET-DIGILOG- LAAS/CNRS contract, April (1991).
- ↑ P. Del Moral, G. Rigal, and G. Salut. "Nonlinear and non Gaussian particle filters applied to inertial platform repositioning." LAAS-CNRS, Toulouse, Research Report no. 92207, STCAN/DIGILOG-LAAS/CNRS Convention STCAN no. A.91.77.013, (94p.) September (1991).
- ↑ P. Del Moral, G. Rigal, and G. Salut. "Estimation and nonlinear optimal control: Particle resolution in filtering and estimation: Experimental results". Convention DRET no. 89.34.553.00.470.75.01, Research report no.2 (54p.), January (1992).
- ↑ P. Del Moral, G. Rigal, and G. Salut. "Estimation and nonlinear optimal control: Particle resolution in filtering and estimation: Theoretical results". Convention DRET no. 89.34.553.00.470.75.01, Research report no.3 (123p.), October (1992).
- ↑ P. Del Moral, J.-Ch. Noyer, G. Rigal, and G. Salut. "Particle filters in radar signal processing: detection, estimation and air targets recognition". LAAS-CNRS, Toulouse, Research report no. 92495, December (1992).
- ↑ P. Del Moral, G. Rigal, and G. Salut. "Estimation and nonlinear optimal control: Particle resolution in filtering and estimation". Studies on: Filtering, optimal control, and maximum likelihood estimation. Convention DRET no. 89.34.553.00.470.75.01. Research report no.4 (210p.), January (1993).
- ↑ Del Moral, Pierre (1998). "Measure Valued Processes and Interacting Particle Systems. Application to Non Linear Filtering Problems". Annals of Applied Probability (Publications du Laboratoire de Statistique et Probabilités, 96-15 (1996) ed.). 8 (2): 438–495. CiteSeerX 10.1.1.55.5257. doi:10.1214/aoap/1028903535.
- ↑ Crisan, Dan; Gaines, Jessica; Lyons, Terry (1998). "Convergence of a branching particle method to the solution of the Zakai". SIAM Journal on Applied Mathematics. 58 (5): 1568–1590. doi:10.1137/s0036139996307371. S2CID 39982562.
- ↑ Crisan, Dan; Lyons, Terry (1997). "Nonlinear filtering and measure-valued processes". Probability Theory and Related Fields. 109 (2): 217–244. doi:10.1007/s004400050131. S2CID 119809371.
- ↑ Crisan, Dan; Lyons, Terry (1999). "A particle approximation of the solution of the Kushner–Stratonovitch equation". Probability Theory and Related Fields. 115 (4): 549–578. doi:10.1007/s004400050249. S2CID 117725141.
- ↑ Crisan, Dan; Del Moral, Pierre; Lyons, Terry (1999). "Discrete filtering using branching and interacting particle systems" (PDF). Markov Processes and Related Fields. 5 (3): 293–318.
- ↑ Del Moral, Pierre; Guionnet, Alice (1999). "On the stability of Measure Valued Processes with Applications to filtering". C. R. Acad. Sci. Paris. 39 (1): 429–434.
- ↑ Del Moral, Pierre; Guionnet, Alice (2001). "On the stability of interacting processes with applications to filtering and genetic algorithms". Annales de l'Institut Henri Poincaré. 37 (2): 155–194. Bibcode:2001AnIHP..37..155D. doi:10.1016/s0246-0203(00)01064-5.
- ↑ Ripley, B. D. (1987). Stochastic Simulation. Wiley & Sons.
- ↑ 54.0 54.1 Sawilowsky, Shlomo S. (2003). "You think you've got trivials?". Journal of Modern Applied Statistical Methods. 2 (1): 218–225. doi:10.22237/jmasm/1051748460.
- ↑ Kalos, Malvin H.; Whitlock, Paula A. (2008). Monte Carlo Methods. Wiley-VCH. ISBN 978-3-527-40760-6.
- ↑ Shojaeefard, MH; Khalkhali, A; Yarmohammadisatri, Sadegh (2017). "An efficient sensitivity analysis method for modified geometry of Macpherson suspension based on Pearson Correlation Coefficient". Vehicle System Dynamics. 55 (6): 827–852. Bibcode:2017VSD....55..827S. doi:10.1080/00423114.2017.1283046. S2CID 114260173.
- ↑ Davenport, J. H. (1992). "Primality testing revisited". Papers from the international symposium on Symbolic and algebraic computation - ISSAC '92. Proceeding ISSAC '92 Papers from the International Symposium on Symbolic and Algebraic Computation. pp. 123–129. CiteSeerX 10.1.1.43.9296. doi:10.1145/143242.143290. ISBN 978-0-89791-489-5. S2CID 17322272.
- ↑ Route, Matthew (August 10, 2017). "Radio-flaring Ultracool Dwarf Population Synthesis". The Astrophysical Journal. 845 (1): 66. arXiv:1707.02212. Bibcode:2017ApJ...845...66R. doi:10.3847/1538-4357/aa7ede. S2CID 118895524.
- ↑ Vose 2000, p. 13
- ↑ Vose 2000, p. 16
- ↑ Jia, Xun; Ziegenhein, Peter; Jiang, Steve B (2014). "GPU-based high-performance computing for radiation therapy". Physics in Medicine and Biology. 59 (4): R151–R182. Bibcode:2014PMB....59R.151J. doi:10.1088/0031-9155/59/4/R151. PMC 4003902. PMID 24486639.
- ↑ Hill, R; Healy, B; Holloway, L; Kuncic, Z; Thwaites, D; Baldock, C (Mar 2014). "Advances in kilovoltage x-ray beam dosimetry". Physics in Medicine and Biology. 59 (6): R183–R231. Bibcode:2014PMB....59R.183H. doi:10.1088/0031-9155/59/6/R183. PMID 24584183. S2CID 18082594.
- ↑ Rogers, D W O (2006). "Fifty years of Monte Carlo simulations for medical physics". Physics in Medicine and Biology. 51 (13): R287–R301. Bibcode:2006PMB....51R.287R. doi:10.1088/0031-9155/51/13/R17. PMID 16790908. S2CID 12066026.
- ↑ Baeurle, Stephan A. (2009). "Multiscale modeling of polymer materials using field-theoretic methodologies: A survey about recent developments". Journal of Mathematical Chemistry. 46 (2): 363–426. doi:10.1007/s10910-008-9467-3. S2CID 117867762.
- ↑ Möller, W.; Eckstein, W. (1984-03-01). "Tridyn — A TRIM simulation code including dynamic composition changes". Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms. 2 (1): 814–818. Bibcode:1984NIMPB...2..814M. doi:10.1016/0168-583X(84)90321-5.
- ↑ MacGillivray, H. T.; Dodd, R. J. (1982). "Monte-Carlo simulations of galaxy systems". Astrophysics and Space Science. 86 (2): 419–435. doi:10.1007/BF00683346. S2CID 189849365.
- ↑ Golden, Leslie M. (1979). "The Effect of Surface Roughness on the Transmission of Microwave Radiation Through a Planetary Surface". Icarus. 38 (3): 451–455. Bibcode:1979Icar...38..451G. doi:10.1016/0019-1035(79)90199-4.
- ↑ Mazhdrakov, Metodi; Benov, Dobriyan; Valkanov, Nikolai (2018). The Monte Carlo Method. Engineering Applications. ACMO Academic Press. pp. 250. ISBN 978-619-90684-3-4. https://books.google.com/books?id=t0BqDwAAQBAJ&q=the+monte+carlo+method+engineering+applications+mazhdrakov.
- ↑ Int Panis et al. 2001
- ↑ Int Panis et al. 2002
- ↑ G. A. Bird, Molecular Gas Dynamics, Clarendon, Oxford (1976)
- ↑ Dietrich, S.; Boyd, I. (1996). "A Scalar optimized parallel implementation of the DSMC technique". Journal of Computational Physics. 126 (2): 328–42. Bibcode:1996JCoPh.126..328D. doi:10.1006/jcph.1996.0141.
- ↑ Nabian, Mohammad Amin; Meidani, Hadi (2017-08-28). "Deep Learning for Accelerated Reliability Analysis of Infrastructure Networks". Computer-Aided Civil and Infrastructure Engineering. 33 (6): 443–458. arXiv:1708.08551. Bibcode:2017arXiv170808551N. doi:10.1111/mice.12359. S2CID 36661983.
- ↑ Nabian, Mohammad Amin; Meidani, Hadi (2018). "Accelerating Stochastic Assessment of Post-Earthquake Transportation Network Connectivity via Machine-Learning-Based Surrogates". Transportation Research Board 97th Annual Meeting.
- ↑ Nabian, Mohammad Amin; Meidani, Hadi (2017). "Uncertainty Quantification and PCA-Based Model Reduction for Parallel Monte Carlo Analysis of Infrastructure System Reliability". Transportation Research Board 96th Annual Meeting.
- ↑ Krivtsov, V. V. (2000). Modeling and estimation of the generalized renewal process in repairable system reliability analysis (PhD). University of Maryland, College Park, ISBN/ISSN: 0599725877.
- ↑ Chen, Shang-Ying; Hsu, Kuo-Chin; Fan, Chia-Ming (15 March 2021). "Improvement of generalized finite difference method for stochastic subsurface flow modeling". Journal of Computational Physics. 429: 110002. doi:10.1016/J.JCP.2020.110002.
- ↑ Climate Change 2013 The Physical Science Basis (PDF). Cambridge University Press. 2013. p. 697. ISBN 978-1-107-66182-0. Retrieved 2 March 2016.
- ↑ Ojeda & et al. 2009,
- ↑ Milik, M.; Skolnick, J. (Jan 1993). "Insertion of peptide chains into lipid membranes: an off-lattice Monte Carlo dynamics model". Proteins. 15 (1): 10–25. doi:10.1002/prot.340150104. PMID 8451235. S2CID 7450512.
- ↑ Cassey; Smith (2014). "Simulating confidence for the Ellison-Glaeser Index". Journal of Urban Economics. 81: 93. doi:10.1016/j.jue.2014.02.005.
- ↑ Sawilowsky, Shlomo S.; Fahoome, Gail C. (2003). Statistics via Monte Carlo Simulation with Fortran. Rochester Hills, MI: JMASM. ISBN 978-0-9740236-0-1.
- ↑ Spall, James C. (2005). "Monte Carlo Computation of the Fisher Information Matrix in Nonstandard Settings". Journal of Computational and Graphical Statistics. 14 (4): 889–909. CiteSeerX 10.1.1.142.738. doi:10.1198/106186005X78800. S2CID 16090098.
- ↑ Das, Sonjoy; Spall, James C.; Ghanem, Roger (2010). "Efficient Monte Carlo computation of Fisher information matrix using prior information". Computational Statistics & Data Analysis. 54 (2): 272–289. doi:10.1016/j.csda.2009.09.018.
- ↑ Guillaume Chaslot; Sander Bakkes; Istvan Szita; Pieter Spronck. "Monte-Carlo Tree Search: A New Framework for Game AI" (PDF). Sander.landofsand.com. Retrieved 28 October 2017.
- ↑ "Monte Carlo Tree Search - About". Archived from the original on 2015-11-29. Retrieved 2013-05-15.
- ↑ Chaslot, Guillaume M. J. -B; Winands, Mark H. M; Van Den Herik, H. Jaap (2008). Parallel Monte-Carlo Tree Search. Lecture Notes in Computer Science. 5131. pp. 60–71. CiteSeerX 10.1.1.159.4373. doi:10.1007/978-3-540-87608-3_6. ISBN 978-3-540-87607-6.
- ↑ Bruns, Pete. Monte-Carlo Tree Search in the game of Tantrix: Cosc490 Final Report (PDF) (Report).
- ↑ David Silver; Joel Veness. "Monte-Carlo Planning in Large POMDPs" (PDF). 0.cs.ucl.ac.uk. Retrieved 28 October 2017.
- ↑ Lorentz, Richard J (2011). "Improving Monte–Carlo Tree Search in Havannah". Computers and Games. Lecture Notes in Computer Science. 6515. pp. 105–115. Bibcode:2011LNCS.6515..105L. doi:10.1007/978-3-642-17928-0_10. ISBN 978-3-642-17927-3.
- ↑ Tomas Jakl. "Arimaa challenge – comparison study of MCTS versus alpha-beta methods" (PDF). Arimaa.com. Retrieved 28 October 2017.
- ↑ Szirmay–Kalos 2008
- ↑ "How the Coast Guard Uses Analytics to Search for Those Lost at Sea". Dice Insights. 2014-01-03.
- ↑ Lawrence D. Stone; Thomas M. Kratzke; John R. Frost. "Search Modeling and Optimization in USCG's Search and Rescue Optimal Planning System (SAROPS)" (PDF). Ifremer.fr. Retrieved 28 October 2017.
- ↑ Carmona, René; Del Moral, Pierre; Hu, Peng; Oudjane, Nadia (2012). Carmona, René A.; Moral, Pierre Del; Hu, Peng; et al. (eds.). An Introduction to Particle Methods with Financial Applications. Numerical Methods in Finance. Springer Proceedings in Mathematics. 12. Springer Berlin Heidelberg. pp. 3–49. CiteSeerX 10.1.1.359.7957. doi:10.1007/978-3-642-25746-9_1. ISBN 978-3-642-25745-2.
- ↑ Carmona, René; Del Moral, Pierre; Hu, Peng; Oudjane, Nadia (2012). Numerical Methods in Finance. Springer Proceedings in Mathematics. 12. doi:10.1007/978-3-642-25746-9. ISBN 978-3-642-25745-2.
- ↑ Kroese, D. P.; Taimre, T.; Botev, Z. I. (2011). Handbook of Monte Carlo Methods. John Wiley & Sons.
- ↑ Arenas, Daniel J.; Lett, Lanair A.; Klusaritz, Heather; Teitelman, Anne M. (2017). "A Monte Carlo simulation approach for estimating the health and economic impact of interventions provided at a student-run clinic". PLOS ONE. 12 (12): e0189718. Bibcode:2017PLoSO..1289718A. doi:10.1371/journal.pone.0189718. PMC 5746244. PMID 29284026.
- ↑ Elwart, Liz; Emerson, Nina; Enders, Christina; Fumia, Dani; Murphy, Kevin (December 2006). "Increasing Access to Restraining Orders for Low Income Victims of Domestic Violence: A Cost-Benefit Analysis of the Proposed Domestic Abuse Grant Program" (PDF). State Bar of Wisconsin. Archived from the original (PDF) on 6 November 2018. Retrieved 2016-12-12.
- ↑ 100.0 100.1 Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (1996) [1986]. Numerical Recipes in Fortran 77: The Art of Scientific Computing. Fortran Numerical Recipes. 1 (2nd ed.). Cambridge University Press. ISBN 978-0-521-43064-7.
- ↑ MEZEI, M (31 December 1986). "Adaptive umbrella sampling: Self-consistent determination of the non-Boltzmann bias". Journal of Computational Physics. 68 (1): 237–248. Bibcode:1987JCoPh..68..237M. doi:10.1016/0021-9991(87)90054-4.
- ↑ Bartels, Christian; Karplus, Martin (31 December 1997). "Probability Distributions for Complex Systems: Adaptive Umbrella Sampling of the Potential Energy". The Journal of Physical Chemistry B. 102 (5): 865–880. doi:10.1021/jp972280j.
- ↑ Del Moral, Pierre; Doucet, Arnaud; Jasra, Ajay (2006). "Sequential Monte Carlo samplers". Journal of the Royal Statistical Society, Series B. 68 (3): 411–436. arXiv:cond-mat/0212648. doi:10.1111/j.1467-9868.2006.00553.x. S2CID 12074789.
- ↑ Spall, J. C. (2003), Introduction to Stochastic Search and Optimization: Estimation, Simulation, and Control, Wiley, Hoboken, NJ. http://www.jhuapl.edu/ISSO
- ↑ Mosegaard, Klaus; Tarantola, Albert (1995). "Monte Carlo sampling of solutions to inverse problems" (PDF). J. Geophys. Res. 100 (B7): 12431–12447. Bibcode:1995JGR...10012431M. doi:10.1029/94JB03097.
- ↑ Tarantola, Albert (2005). Inverse Problem Theory. Philadelphia: Society for Industrial and Applied Mathematics. ISBN 978-0-89871-572-9.
- ↑ McCracken, D. D., (1955) The Monte Carlo Method, Scientific American, 192(5), pp. 90-97
- ↑ Elishakoff, I., (2003) Notes on Philosophy of the Monte Carlo Method, International Applied Mechanics, 39(7), pp.753-762
- ↑ Grüne-Yanoff, T., & Weirich, P. (2010). The philosophy and epistemology of simulation: A review, Simulation & Gaming, 41(1), pp. 20-50
引用
- Anderson, Herbert L. (1986). "Metropolis, Monte Carlo and the MANIAC" (PDF). Los Alamos Science. 14: 96–108.
- Benov, Dobriyan M. (2016). "The Manhattan Project, the first electronic computer and the Monte Carlo method". Monte Carlo Methods and Applications. 22 (1): 73–79. doi:10.1515/mcma-2016-0102.
- Baeurle, Stephan A. (2009). "Multiscale modeling of polymer materials using field-theoretic methodologies: A survey about recent developments". Journal of Mathematical Chemistry. 46 (2): 363–426. doi:10.1007/s10910-008-9467-3.
- Berg, Bernd A. (2004). Markov Chain Monte Carlo Simulations and Their Statistical Analysis (With Web-Based Fortran Code). Hackensack, NJ: World Scientific. ISBN 978-981-238-935-0.
- Binder, Kurt (1995). The Monte Carlo Method in Condensed Matter Physics. New York: Springer.
- Caflisch, R. E. (1998). Monte Carlo and quasi-Monte Carlo methods. Acta Numerica. 7. Cambridge University Press.
- Davenport, J. H. (1992). "Primality testing revisited". Papers from the international symposium on Symbolic and algebraic computation - ISSAC '92. pp. 123–129. doi:10.1145/143242.143290. ISBN 978-0-89791-489-5.
- Doucet, Arnaud; Freitas, Nando de; Gordon, Neil (2001). Sequential Monte Carlo methods in practice. New York: Springer. ISBN 978-0-387-95146-1.
- Eckhardt, Roger (1987). "Stan Ulam, John von Neumann, and the Monte Carlo method" (PDF). Los Alamos Science (15): 131–137.
- Fishman, G. S. (1995). Monte Carlo: Concepts, Algorithms, and Applications. New York: Springer. ISBN 978-0-387-94527-9.
- C. Forastero and L. Zamora and D. Guirado and A. Lallena (2010). "A Monte Carlo tool to simulate breast cancer screening programmes". Phys. Med. Biol. 55 (17): 5213–5229. Bibcode:2010PMB....55.5213F. doi:10.1088/0031-9155/55/17/021. PMID 20714045.
- Golden, Leslie M. (1979). "The Effect of Surface Roughness on the Transmission of Microwave Radiation Through a Planetary Surface". Icarus. 38 (3): 451–455. Bibcode:1979Icar...38..451G. doi:10.1016/0019-1035(79)90199-4.
- Gould, Harvey; Tobochnik, Jan (1988). An Introduction to Computer Simulation Methods, Part 2, Applications to Physical Systems. Reading: Addison-Wesley. ISBN 978-0-201-16504-3.
- Grinstead, Charles; Snell, J. Laurie (1997). Introduction to Probability. American Mathematical Society. pp. 10–11. https://archive.org/details/flooved3489.
- Hammersley, J. M.; Handscomb, D. C. (1975). Monte Carlo Methods. London: Methuen. ISBN 978-0-416-52340-9.
- Hartmann, A.K. (2009). Practical Guide to Computer Simulations. World Scientific. ISBN 978-981-283-415-7. http://www.worldscibooks.com/physics/6988.html.
- Hubbard, Douglas (2007). How to Measure Anything: Finding the Value of Intangibles in Business. John Wiley & Sons. p. 46. https://archive.org/details/howtomeasureanyt00hubb_773.
- Hubbard, Douglas (2009). The Failure of Risk Management: Why It's Broken and How to Fix It. John Wiley & Sons.
- Kahneman, D.; Tversky, A. (1982). Judgement under Uncertainty: Heuristics and Biases. Cambridge University Press.
- Kalos, Malvin H.; Whitlock, Paula A. (2008). Monte Carlo Methods. Wiley-VCH. ISBN 978-3-527-40760-6.
- Kroese, D. P.; Taimre, T.; Botev, Z.I. (2011). Handbook of Monte Carlo Methods. New York: John Wiley & Sons. p. 772. ISBN 978-0-470-17793-8. http://www.montecarlohandbook.org.
- MacGillivray, H. T.; Dodd, R. J. (1982). "Monte-Carlo simulations of galaxy systems". Astrophysics and Space Science. 86 (2): 419–435. doi:10.1007/BF00683346.
- MacKeown, P. Kevin (1997). Stochastic Simulation in Physics. New York: Springer. ISBN 978-981-3083-26-4.
- Metropolis, N. (1987). "The beginning of the Monte Carlo method" (PDF). Los Alamos Science (1987 Special Issue dedicated to Stanislaw Ulam): 125–130.
- Metropolis, N.; Rosenbluth, Arianna W.; Rosenbluth, Marshall N.; Teller, Augusta H.; Teller, Edward (1953). "Equation of State Calculations by Fast Computing Machines". Journal of Chemical Physics. 21 (6): 1087. Bibcode:1953JChPh..21.1087M. doi:10.1063/1.1699114.
- Metropolis, N.; Ulam, S. (1949). "The Monte Carlo Method". Journal of the American Statistical Association. 44 (247): 335–341. doi:10.1080/01621459.1949.10483310. JSTOR 2280232. PMID 18139350.
- Milik, M.; Skolnick, J. (Jan 1993). "Insertion of peptide chains into lipid membranes: an off-lattice Monte Carlo dynamics model". Proteins. 15 (1): 10–25. doi:10.1002/prot.340150104. PMID 8451235.
- Mosegaard, Klaus; Tarantola, Albert (1995). "Monte Carlo sampling of solutions to inverse problems" (PDF). J. Geophys. Res. 100 (B7): 12431–12447. Bibcode:1995JGR...10012431M. doi:10.1029/94JB03097.
- P. Ojeda; M. Garcia; A. Londono; N.Y. Chen (Feb 2009). "Monte Carlo Simulations of Proteins in Cages: Influence of Confinement on the Stability of Intermediate States". Biophys. J. 96 (3): 1076–1082. Bibcode:2009BpJ....96.1076O. doi:10.1529/biophysj.107.125369. PMC 2716574. PMID 18849410.
- Int Panis, L.; de Nocker, L.; De Vlieger, I.; Torfs, R. (2001). "Trends and uncertainty in air pollution impacts and external costs of Belgian passenger car traffic". International Journal of Vehicle Design. 27 (1–4): 183–194. doi:10.1504/IJVD.2001.001963.
- Int Panis, L.; Rabl, A.; de Nocker, L.; Torfs, R. (2002). Sturm, P. (ed.). "Diesel or Petrol ? An environmental comparison hampered by uncertainty". Mitteilungen Institut für Verbrennungskraftmaschinen und Thermodynamik. Technische Universität Graz Austria. Heft 81 Vol 1: 48–54.
- Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (1996). Numerical Recipes in Fortran 77: The Art of Scientific Computing. Fortran Numerical Recipes. 1 (2nd ed.). Cambridge University Press. ISBN 978-0-521-43064-7.
- Ripley, B. D. (1987). Stochastic Simulation. Wiley & Sons.
- Robert, C.; Casella, G. (2004). Monte Carlo Statistical Methods (2nd ed.). New York: Springer. ISBN 978-0-387-21239-5. https://archive.org/details/springer_10.1007-978-1-4757-4145-2.
- Rubinstein, R. Y.; Kroese, D. P. (2007). Simulation and the Monte Carlo Method (2nd ed.). New York: John Wiley & Sons. ISBN 978-0-470-17793-8.
- Savvides, Savvakis C. (1994). "Risk Analysis in Investment Appraisal" (PDF). Project Appraisal Journal. 9 (1). doi:10.2139/ssrn.265905.
- Sawilowsky, Shlomo S.; Fahoome, Gail C. (2003). Statistics via Monte Carlo Simulation with Fortran. Rochester Hills, MI: JMASM. ISBN 978-0-9740236-0-1.
- Sawilowsky, Shlomo S. (2003). "You think you've got trivials?". Journal of Modern Applied Statistical Methods. 2 (1): 218–225. doi:10.22237/jmasm/1051748460.
- Silver, David; Veness, Joel (2010). "Monte-Carlo Planning in Large POMDPs" (PDF). In Lafferty, J.; Williams, C. K. I.; Shawe-Taylor, J.; Zemel, R. S.; Culotta, A. (eds.). Advances in Neural Information Processing Systems 23. Neural Information Processing Systems 2010. Neural Information Processing Systems Foundation.
- Szirmay-Kalos, László (2008). Monte Carlo Methods in Global Illumination - Photo-realistic Rendering with Randomization. VDM Verlag Dr. Mueller e.K.. ISBN 978-3-8364-7919-6.
- Tarantola, Albert (2005). Inverse Problem Theory. Philadelphia: Society for Industrial and Applied Mathematics. ISBN 978-0-89871-572-9. http://www.ipgp.jussieu.fr/~tarantola/Files/Professional/SIAM/index.html.
- Vose, David (2008). Risk Analysis, A Quantitative Guide (3rd ed.). John Wiley & Sons.
编者推荐
集智文章推荐
- 研究表明,来自中国的新型冠状病毒肺炎卫生组织的初始数据显示确诊病例的数量呈次指数幂律增长。这是由于采取了有效的遏制和缓解措施,以及人口的行为变化。有鉴于此,本文进行了蒙特卡洛随机漫步研究,以更好地理解基于邻近的传染病扩散,特别是在限制条件下。
课程推荐
- 可以说,AlphaGo标志着现代人工智能最顶尖的技术,它的核心算法就是两块,一块是深度强化学习,另一块就是蒙特卡洛搜索。所谓的深度强化学习是深度学习技术与古老的强化学习技术的混合;而蒙特卡洛搜索则是一种快速的搜索算法,能够通过对战的模拟而完成走棋。AlphaGo巧妙地将深度强化学习、蒙特卡洛搜索等技术融合在了一起,造就了人工智能历史上的深化。本课程将全面解读AlphaGo背后的深度学习技术。
- 蒙特卡罗(Monte Carlo)方法,也称为计算机随机模拟方法,是一种基于"随机数"的计算方法。蒙特卡罗方法与一般计算方法有很大区别,一般计算方法对于解决多维或因素复杂的问题非常困难,而蒙特卡罗方法对于解决这方面的问题却比较简单,原因是它巧妙的采用了用事件发生的"频率"来决定事件的"概率"的方法。本课程详细介绍了蒙特卡罗(Monte Carlo)方法的原理与应用。
文章推荐
- 本文将介绍一种处理数学物理中一类问题的方法的动机和一般描述。这种方法本质上是一种研究微分方程的统计学方法,或者更广泛地说,是研究自然科学各个分支中出现的积分-微分方程的一种统计方法。
本中文词条由栗子CUGB、王婷、Moonscar参与编译和审校,糖糖、SyouTK编辑,如有问题,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。