量子计算
量子计算 Quantum computing是利用量子态的性质(如叠加原理和量子纠缠)来执行计算。执行量子计算的设备被称为量子计算机。[1]量子计算机相比传统计算机能够从根本上更快地解决某些计算问题,比如整数分解(这是RSA 加密的基础)。量子计算是量子信息科学的一个子领域。随着该领域转向制药、数据安全和其他应用中的实际运用,预计在未来几年内会得到扩展[2]。
量子计算始于20世纪80年代早期,当时物理学家保罗·贝尼奥夫 Paul Benioff提出了图灵机的量子力学模型。[3]理查德·费曼 Richard Feynman和尤里·曼宁 Yuri Manin后来提出,量子计算机有潜力去模拟传统计算机所无法模拟的东西。[4][5]1994年,Peter Shor 开发了一种量子算法,用于整数分解,这种算法有可能解密 rsa 加密的通信。[6]尽管自20世纪90年代后期以来,实验取得了进展,但大多数研究人员认为,“容错量子计算机仍然是一个相当遥远的梦想。”[7]近年来,量子计算研究的投资在公共和私营部门都有所增加。[8][9]2019年10月23日,谷歌AI与美国宇航局(NASA)合作,声称已经执行了在任何传统计算机上都不可能完成的量子计算。[10]
量子计算有几种模型,包括量子电路模型、量子图灵机、绝热量子计算机、单向量子计算机和各种量子细胞自动机。使用最广泛的模型基于“量子比特”或“量子位 qubit”的量子电路模型 Quantum circuits 。它在某种程度上类似于经典计算中的“比特”。一个量子比特可以处于1或0的量子态,或者处于1和0的叠加态。然而,当量子比特被测量时,测量结果只能是0或1; 这两种结果发生的概率取决于量子比特在被测量之前所处的量子状态。计算是通过量子逻辑门 Quantum logic gates操纵量子比特来完成的,这在某种程度上类似于经典逻辑门。
目前量子计算机的物理实现努力集中在transmons、离子阱 ion traps和拓扑量子计算机 topological quantum computers等技术上,这些技术旨在创造高质量的量子比特。[1] 量子比特的设计方式可能不同,这取决于量子计算机的计算模型,是量子逻辑门、量子退火 quantum annealing还是绝热量子计算 adiabatic quantum computation。目前,构建有用的量子计算机还存在一些较大的阻碍。由于受到量子退相干 quantum decoherence和量子态保真度 state fidelity的影响,维持量子比特的量子状态尤其困难。因此,量子计算机需要纠错。[11][12]
任何可以由经典计算机解决的计算问题,原则上也可以由量子计算机解决。[13]反过来,任何可以由量子计算机解决的计算问题也可以由经典计算机解决,至少在给予足够时间的情况下,换句话说,量子计算机遵循 Church-Turing 理论。虽然这意味着量子计算机在可计算性方面没有比传统计算机多提供额外的优势,但在理论上,但量子算法对于某些问题的时间复杂度明显低于相应的已知经典算法。值得注意的是,人们相信量子计算机能够快速解决某些问题,而这些问题是任何传统计算机都无法在可行的时间内解决的——这一壮举被称为“量子至上 quantum supremacy”。关于量子计算机问题的计算复杂性的研究被称为量子复杂性理论 Quantum complexity theory。
量子计算
当前流行的量子计算模型用量子逻辑门网络来描述计算。
一个由[math]\displaystyle{ n }[/math] 比特信息组成的内存有 [math]\displaystyle{ 2^n }[/math] 种可能的状态。因此,一个代表所有内存状态的向量具有 [math]\displaystyle{ 2^n }[/math] 个条目(每个状态一个)。这个向量被看作是一个概率向量,它代表这样一个事实——内存总是在某个特定的状态下被访问。
在经典的观点中,一个条目的值为1(即有100% 的概率处于这种状态) ,所有其他条目都是零。在量子力学中,概率向量被推广到密度算子 Density operators。它是技术上严格的量子逻辑门的数学基础,但介绍的时候通常首先引入中间量子态的向量形式,因为它在概念上比较简单。为了简单起见,本文着重讨论量子态向量形式。
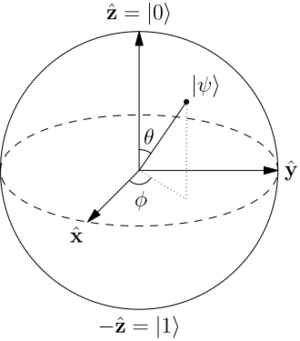
我们首先考虑一个只有1位的简单内存。这种内存只有0或1两种状态。我们可以用狄拉克符号 Dirac notation来表示这段内存的状态,因此
[math]\displaystyle{ |0\rangle := \begin{pmatrix} 1 \\ 0 \end{pmatrix};\quad |1\rangle := \begin{pmatrix} 0 \\ 1 \end{pmatrix} }[/math]
一个量子内存可能处在两种经典状态的量子叠加态中的任意一种状态[math]\displaystyle{ |\psi\rangle }[/math]:
[math]\displaystyle{ |0\rangle }[/math] and [math]\displaystyle{ |1\rangle }[/math]:
[math]\displaystyle{
|\psi\rangle := \alpha\,|0\rangle + \beta\,|1\rangle
= \begin{pmatrix} \alpha \\ \beta \end{pmatrix};\quad
|\alpha|^2 + |\beta|^2 = 1.
}[/math]
一般来说,系数 [math]\displaystyle{ \alpha }[/math] 和 [math]\displaystyle{ \beta }[/math]都是复数。在这种情况下,信息的一个量子比特被编码到量子内存中。状态[math]\displaystyle{ |\psi\rangle }[/math]本身不是一个概率向量,但可以通过测量操作与概率向量相连。如果量子内存被测量以确定其状态是 [math]\displaystyle{ |0\rangle }[/math] 还是[math]\displaystyle{ |1\rangle }[/math](这被称为计算基础测量) ,那么0状态将以概率 [math]\displaystyle{ |\alpha|^2 }[/math]被观测到,而1状态将以概率 [math]\displaystyle{ |\beta|^2 }[/math]被观测到。数字 [math]\displaystyle{ \alpha }[/math] 和 [math]\displaystyle{ \beta }[/math]被称为量子幅值 Quantum amplitudes。
这种单比特量子存储器的状态可以通过量子逻辑门来控制,类似于用经典逻辑门来控制经典存储器。对经典和量子计算都很重要的门是非门 NOT gate,它可以用矩阵表示
[math]\displaystyle{ X := \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}. }[/math]
在数学上,逻辑门作用于量子态向量可以建模成矩阵乘法。因此 [math]\displaystyle{ X|0\rangle = |1\rangle }[/math] 和 [math]\displaystyle{ X|1\rangle = |0\rangle }[/math]。
单个量子比特门的数学可以通过两种重要的方式扩展到对多量子比特量子存储器的操作。一种方法是简单地选择一个量子位并将该门应用于目标量子位,同时不影响其余的内存。另一种方法是,只有当内存的另一部分处于被需要状态时,才将门应用于目标量子位。这两种选择可以用另一个例子来说明。两比特量子存储器的可能状态包括
[math]\displaystyle{ |00\rangle := \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix};\quad |01\rangle := \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix};\quad |10\rangle := \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix};\quad |11\rangle := \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix}. }[/math]
然后,量子受控非门 CNOT gate可以用以下矩阵表示:
[math]\displaystyle{ \operatorname{CNOT} := \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{pmatrix}. }[/math]
作为这个定义的数学推论,[math]\displaystyle{ CNOT|00\rangle = |00\rangle }[/math], [math]\displaystyle{ CNOT|01\rangle = |01\rangle }[/math], [math]\displaystyle{ CNOT|10\rangle = |11\rangle }[/math], 和[math]\displaystyle{ CNOT|11\rangle = |10\rangle }[/math]。换句话说,当且仅当第一个量子位处于状态 [math]\displaystyle{ |1\rangle }[/math] 时,CNOT 才对第二个量子位应用 非门([math]\displaystyle{ X }[/math])。如果第一个量子位是 [math]\displaystyle{ |0\rangle }[/math],则对任何一个量子位都不做处理。
总之,量子计算可以描述为一个由量子逻辑门和测量组成的网络。任何测量都可以推迟到量子计算结束时进行,尽管这种推迟可能会带来计算成本。由于这种延迟测量的可能性,大多数量子电路描述的网络只有量子逻辑门而没有测量。更多信息可以参考以下文章:通用量子计算机,Shor 算法,Grover算法,Deutsch-Jozsa 算法,振幅放大,量子傅里叶变换 Quantum Fourier transform,量子门,量子绝热算法和量子误差修正 Quantum error correction。
任何量子计算都可以表示为一个量子逻辑门网络,量子逻辑门是门中的一个小类。使这种结构成为可能的一类门的被称为通用门集合。常见的这种集合包括所有的单量子比特门以及上面的 量子受控非门CNOT 门。这意味着任何量子计算都可以通过执行一系列带有 量子受控非门CNOT 门的单量子比特门来完成。虽然这个门集合是无限的,但是它可以通过引用 Solovay-Kitaev 定理被一个有限的门集合来代替。多个量子位可以用 Qsphere 来表示。
潜在应用
密码学
整数因式分解 Integer factorization是公钥密码系统 Public key cryptographic systems安全性的基础,如果一个大整数是几个素数的乘积(例如,两个300位素数的乘积)[14],那么在普通计算机上计算是不可行的。相比之下,量子计算机可以有效地解决这个问题,使用肖尔Shor算法来寻找它的因子。这种能力将使量子计算机能够破解目前使用的许多密码系统,也就是说,可以用多项式时间(整数位数)算法来解决这个问题。特别是目前流行的公钥密码算法大多是基于大整数因式分解或离散对数问题的困难性,而这两个问题都可以用肖尔Shor算法来解决。尤其是RSA、Diffie-Hellman和椭圆曲线Diffie-Hellman算法可能会被破解,它们一般用于保护安全网页、加密电子邮件和许多其他类型的数据。破解这些算法将对电子隐私和安全产生重大影响。
然而,其他密码算法似乎并没有被那些算法破解。[15][16]有些公钥算法是基于除整数分解和离散对数问题以外的问题,肖尔Shor算法并不适用于这些问题,例如McEliece密码体制基于编码理论中的一个问题。[15][17]基于格的密码体制也不能被量子计算机破解,寻找一个多项式时间算法来解决二面体隐子群问题 Dihedral hidden subgroup problem,将打破许多基于格的密码体制,这是一个充分研究的开放性问题。[18]已经证明,用Grover算法来暴力破解对称(密钥)算法所需的时间大约相当于基础加密算法的2n/2次调用,而在经典情况下大约需要2n,[19]这意味着对称密钥长度将有效地减半:AES-256应对使用Grover算法的攻击的安全性与AES-128应对经典暴力搜索的安全性相同(参见密钥大小)。
量子密码学 Quantum cryptography可以实现公开密钥加密的一些功能。因此,面对量子黑客攻击时,基于量子的加密系统可能比传统系统更安全。[20]
量子搜索
承认多项式量子加速的问题最著名的例子是非结构化搜索,从列表中找到一个标记项。[math]\displaystyle{ n }[/math]数据库中的项目。这可以通过使用Grover算法解决[math]\displaystyle{ O(\sqrt{n}) }[/math] 对数据库的查询,比[math]\displaystyle{ \Omega(n) }[/math]经典算法所需的查询。在这种情况下,优势不仅是可证明的,而且是最优的:已经表明,格罗弗的算法为任意数量的预言机查找提供了找到所需元素的最大可能概率。
可以通过Grover算法解决的问题有以下属性:
- 在可能的答案集合中没有可搜索的结构,
- 要检查的可能答案的数量与算法的输入数量相同,并且
- 存在一个布尔函数,它计算每个输入并确定它是否是正确的答案
对于具有所有这些性质的问题,Grover算法在量子计算机上的运行时间将按输入(或数据库中元素)数量的平方根进行缩放,而不是经典算法的线性缩放。一类可以应用Grover算法的一般问题是[21]布尔可满足性问题。在本例中,算法迭代使用的“数据库”是所有可能答案的数据库。这方面的一个例子(也是可能的)应用是一个密码破解器试图猜测加密文件或系统的密码或密钥。对称密码例如Triple DES和Advanced Encryption Standard(AES)特别容易受到此类攻击。{{引文需要{日期=2019年11月}}量子计算的这一应用是政府机构主要感兴趣的。[22]
量子模拟
由于化学和纳米技术依赖于对量子系统的理解,而这种系统不可能以经典的方式进行有效的模拟,许多人相信量子模拟将是量子计算最重要的应用之一。[23]量子模拟也可以用来模拟原子和粒子在异常条件下的行为,例如对撞机内部的反应。 [24]
量子退火与绝热优化
量子退火或绝热量子计算依赖绝热定理进行计算。在一个简单的哈密顿体系中,系统处于基态,这个哈密顿体系慢慢演化成一个更复杂的哈密顿体系,其基态代表问题的解决方案。绝热定理指出,如果演化足够慢,系统将在整个过程中始终保持在基态。
以其发现者 Harrow,Hassidim和 Lloyd命名的线性方程组的量子算法,或称HHL 算法,有望提供比经典算法更快的速度。[25]
量子至上
John Preskill引入了“量子至上 Quantum supremacy”一词来指量子计算机在某一领域相对于经典计算机所具有的假设加速优势。[26]Google在2017年宣布,它预计将在今年年底实现量子霸权,但这并没有实现。IBM在2018年表示,最好的经典计算机将在大约五年内完成一些实际任务,并将量子优势测试视为未来潜在的基准。[27]尽管像Gil Kalai这样的怀疑论者怀疑量子霸权是否会实现,[28][29]据报道,2019年10月,与谷歌AI Quantum联合创建的Sycamore processor实现了量子优势[30],它的计算速度是世界上最快的计算机 Summit的300多万倍。[31]比尔 · 安鲁在1994年发表的一篇论文中对量子计算机的实用性表示怀疑。[32]Paul Davies认为,一台400 量子比特的计算机甚至会与[[全息原理]所隐含的宇宙信息界发生冲突。[33]
阻碍
建造大型量子计算机面临许多技术挑战。[34]物理学家David DiVincenzo为一台实用的量子计算机列出了以下要求 :[35]
- 物理上可扩展以增加量子比特的数量
- 可以初始化为随机值的量子位
- 比退相干时间快的量子门
- 通用门组
- 易于读取的量子位
寻找量子计算机的零部件也非常困难。许多量子计算机,比如谷歌和 IBM 制造的计算机,需要核研究的Hemien-3,以及只有日本Coax Co.公司制造的特殊超导电缆。[36]
多量子比特系统的控制需要产生和协调大量的电信号并保证严格和确定的时序分辨率。这导致了量子控制器的发展,它能够接通量子比特。扩展这些系统以支持越来越多的量子比特是量子计算机扩展的额外挑战。
量子退相干
构建量子计算机的最大挑战之一是控制或消除量子退相干。这通常意味着将系统与其环境隔离,因为与外部世界的交互会导致系统退相干。然而,也存在其他的退相干源。例如量子门,晶格振动和用于实现量子比特的物理系统的背景热核自旋。退相干是不可逆的,因为它实际上是非酉的,如果不能避免的话,通常也应该高度控制。候选系统的退相干时间,特别是横向弛豫时间“T”2(对于 NMR和MRI技术,也称为“去相位时间”),在低温下通常在纳秒到秒之间。.[37]目前,一些量子计算机要求将量子比特冷却到20毫开尔文,以防止严重的退相干。[38]2020年的一项研究认为,尽管如此,诸如[宇宙射线]]这样的电离辐射仍能导致某些系统在毫秒范围内退凝。[39]
因此,耗时的任务可能会使一些量子算法无法操作,因为维持量子位的状态足够长的时间最终会破坏这些叠加。[40]
这些问题对于光学方法来说更为困难,因为光学方法的时间数量级更小,而克服这些问题的常用方法是光脉冲整形。错误率通常和操作时间与退相干时间的比率成正比,因此任何操作都必须比退相干时间快得多。
如量子阈值定理所述,如果错误率足够小,则可以利用量子纠错来抑制误差和退相干。如果纠错方案能够比退相干引入的错误更快地纠正错误,则会使得总计算时间比退相干时间长。假设噪声是去极化的,则容错计算中每个门所需的错误率经常引用的数字是10-3。
满足这种可伸缩性条件对于各种系统都是可能的。然而,纠错的使用带来了大量增加所需量子比特的代价。使用Shor算法对整数进行因子运算所需的数量级仍然是多项式的,并且被认为在L和L2之间,其中L是要被分解的数量中的量子位数;纠错算法将使这个数字膨胀一个额外的系数L。对于1000位的数字,这意味着需要大约104位没有纠错。[41]通过纠错,这个数字将上升到大约107位。计算时间约为L2 或约 107步,在主频为1兆赫时,大约10秒。
解决稳定退相干问题的一个非同寻常的方法是用任意子,准粒子作为线程,依靠辫子理论来形成稳定的逻辑门[42][43]
物理学家Mikhail Dyakonov对量子计算表示了以下怀疑:
- “因此,描述这样一个有用的量子计算机在任何给定时刻的状态的连续参数的数量必须是...大约10300... 我们能不能学会控制定义这样一个系统量子态的超过10300个连续可变的参数?我的回答很简单“不,永远不会”。[44][45]
发展
量子计算模型
有许多量子计算模型,其区别在于计算被分解时的基本元素。具有实践重要性的四种主要模式是:
- 量子电路(计算分解为几个量子比特的序列量子门)
- 单向量子计算机(将计算分解为一个量子比特测量序列,应用于高度纠缠的初始状态或团簇状态)
- 绝热量子计算,基于量子退火(计算分解为初始哈密顿量到最终哈密顿量的缓慢连续变换,其基态包含解)
- 拓扑量子计算机[47] (在二维晶格中分解成任意子编织的计算)
量子图灵机理论上很重要,但是这个模型的物理实现是不可行的。所有四种计算模型被证明是等价的; 每种模型只需要不超过多项式的开销就可以模拟另一种模型。
物理实现
对于量子计算机的物理实现,人们正在寻找许多不同的候选方案,其中包括(以实现量子比特的物理系统为区别):
- 超导量子计算[48][49](由小型超导电路状态实现的量子比特)
- 束缚离子量子计算机(由束缚离子的内部状态实现的量子比特)
- 光学晶格中的中性原子(由被困在光学晶格中的中性原子的内部状态实现的量子比特)[50][51]
- 量子点计算机,基于自旋(例如Divencenzo损失差额量子计算机[52])(量子比特由俘获电子的自旋态给出)
- 基于空间的量子点计算机(由双量子点中的电子位置给出的量子比特)[53]
- 使用工程量子阱进行量子计算,原则上可以建造在室温下工作的量子计算机[54][55]
- 耦合的量子线(量子比特由一对量子线实现,量子线通过一对量子线耦合量子点接触)[56][57][58]
- 核磁共振量子计算机(NMRQC)利用溶液中分子的核磁共振来实现,其中量子比特由溶解分子中的核自旋提供,并被无线电波探测
- 固态NMR Kane量子计算机](由磷电子供体在硅中的核自旋态实现的量子比特)
- 量子计算机上的电子(量子比特是电子的自旋)
- 腔量子电动力学(CQED)(由与高精细腔耦合的被俘获原子的内部状态提供的量子比特)
- 单分子磁体(量子比特由自旋态给出)[59]
- 基于富勒烯的电子顺磁共振[60]量子计算机(基于内表面富勒烯)
- 非线性光学量子计算机(通过线性和非线性光学元件处理光的不同模式状态实现的量子比特)[61][62]
- 线性光学量子计算(通过线性元件(如反射镜、分束器和移相器处理光的不同模式状态实现的量子比特)[63]
- 金刚石量子计算机[64][65][66](通过金刚石中氮空位中心的电子或核自旋实现的量子比特)
- 基于玻色-爱因斯坦凝聚体的量子计算机[67]
- 基于晶体管的量子计算机——使用静电阱夹带正空穴的串量子计算机
- 稀土金属离子掺杂无机晶体量子计算机[68][69](量子位由内部的电子状态来实现掺杂剂中的光纤)
- 基于类金属碳纳米球的量子计算机[70]
大量的候选方案表明,尽管量子计算技术发展迅速,但仍处于初级阶段。
与可计算性和复杂性理论的关系
可计算性理论
经典计算机可以解决的任何计算问题也可以由量子计算机解决。[71]直觉上,这是因为人们相信,所有物理现象(包括经典计算机的运行),都可以用量子力学来描述,而这是量子计算机操作的基础。
相反,量子计算机可以解决的任何问题也可以用经典计算机来解决;或者更正式地说,任何量子计算机都可以用图灵机模拟量子计算机。换句话说,量子计算机在可计算性方面没有比传统计算机多提供额外的优势。这意味着量子计算机不能解决像停止问题一样的不可判定问题,量子计算机的存在也并不能否定丘奇-图灵论点。
到目前为止,量子计算机还不能满足强丘奇理论。虽然假想的机器已经实现,但一个通用的量子计算机还没有被物理构造出来。丘奇理论的强版本需要一台物理计算机实体,所以还没有一台量子计算机能够满足强大的丘奇理论。
量子复杂性理论
虽然量子计算机无法解决经典计算机已经无法解决的任何问题,但人们怀疑它们可以比经典计算机更快地解决某些问题。例如,众所周知,量子计算机可以有效地分解整数,而经典计算机则不然。
可以由具有有界误差的量子计算机有效解决的一类问题称为BQP,意思是“有界误差,量子,多项式时间”。更正式地说,BQP 是一类可以由多项式时间量子图灵机解决的问题,错误概率最多为 1/3。作为一类概率问题,BQP 是BPP(“有界误差,概率,多项式时间”)的量子对应物,BPP(“有界误差,概率,多项式时间”)是一类可以由具有有限误差的多项式时间概率图灵机解决的问题。[72] 众所周知,BPP[math]\displaystyle{ \subseteq }[/math]BQP和广泛怀疑 BQP[math]\displaystyle{ \subsetneq }[/math]BPP,这直观地意味着量子计算机在时间复杂度方面比经典计算机更强大。[73]
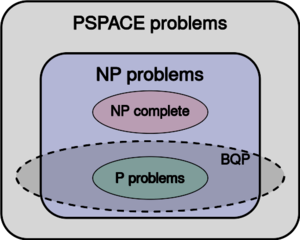
BQP 与P、NP和PSPACE的确切关系尚不清楚。但是,众所周知, P[math]\displaystyle{ \subseteq }[/math]BQP[math]\displaystyle{ \subseteq }[/math]空间;也就是说,所有确定性经典计算机可以有效解决的问题也可以由量子计算机有效解决,所有量子计算机可以有效解决的问题也可以由具有多项式空间资源的确定性经典计算机解决. 进一步怀疑 BQP 是 P 的严格超集,这意味着存在量子计算机可以有效解决的问题,而确定性经典计算机则无法有效解决。例如,整数分解和离散对数问题已知在 BQP 中并且被怀疑在 P 之外。 关于 BQP 与 NP 的关系,除了一些被认为不在 P 中的 NP 问题也在 BQP(整数分解和例如,离散对数问题都在 NP 中)。怀疑是 NP[math]\displaystyle{ \nsubseteq }[/math]BQP; 也就是说,人们认为存在量子计算机无法有效解决的可有效检查的问题。作为这种信念的直接结果,也有人怀疑 BQP 与NP 完全问题的类别不相交(如果 NP 完全问题在 BQP 中,那么从NP难度可以得出NP中的所有问题都在BQP)。[75]
BQP 与基本经典复杂度类的关系可以总结如下:
- [math]\displaystyle{ \mathsf{P \subseteq BPP \subseteq BQP \subseteq PP \subseteq PSPACE} }[/math]
众所周知,BQP 包含在复杂性类#P(或更准确地说,在决策问题的相关类 P#P),[75]它是PSPACE的子类。
据推测,物理学的进一步进步可能会导致更快的计算机。例如,已经表明基于玻姆力学 Bohmian Mechanics的非局部隐变量量子计算机可以实现对[math]\displaystyle{ N }[/math]-- 项目数据库最多[math]\displaystyle{ O(\sqrt[3]{N}) }[/math]步,比Grover算法略有加速,它运行在[math]\displaystyle{ O(\sqrt{N}) }[/math]步。但是请注意,这两种搜索方法都不允许量子计算机在多项式时间内解决NP完全问题。[76] 量子引力理论,例如M 理论和圈量子引力,可能允许建造速度更快的计算机。然而,由于时间问题,在这些理论中定义计算是一个悬而未决的问题;也就是说,在这些物理理论中,目前没有明显的方法来描述观察者在某个时间点向计算机提交输入然后在稍后的时间点接收输出意味着什么。[77][78]
参考文献
- ↑ 1.0 1.1 The National Academies of Sciences, Engineering, and Medicine (2019). Quantum Computing : Progress and Prospects (2018). Washington, DC: National Academies Press. p. I-5. doi:10.17226/25196. ISBN 978-0-309-47969-1. OCLC 1081001288.
- ↑ "Scopus for Corporate Research & Development".
- ↑ Benioff, Paul (1980). "The computer as a physical system: A microscopic quantum mechanical Hamiltonian model of computers as represented by Turing machines". Journal of Statistical Physics. 22 (5): 563–591. Bibcode:1980JSP....22..563B. doi:10.1007/bf01011339.
- ↑ Feynman, Richard (June 1982). "Simulating Physics with Computers" (PDF). International Journal of Theoretical Physics. 21 (6/7): 467–488. Bibcode:1982IJTP...21..467F. doi:10.1007/BF02650179. Archived from the original (PDF) on 8 January 2019. Retrieved 28 February 2019.
- ↑ Manin, Yu. I. (1980) (in Russian). Vychislimoe i nevychislimoe. Sov.Radio. pp. 13–15. Archived from the original on 2013-05-10. https://web.archive.org/web/20130510173823/http://publ.lib.ru/ARCHIVES/M/MANIN_Yuriy_Ivanovich/Manin_Yu.I._Vychislimoe_i_nevychislimoe.(1980).%5Bdjv%5D.zip. Retrieved 2013-03-04.
- ↑ Breaking RSA Encryption with a Quantum Computer: Shor's Factoring Algorithm
- ↑ John Preskill (2018). "Quantum Computing in the NISQ era and beyond". Quantum. 2: 79. arXiv:1801.00862. doi:10.22331/q-2018-08-06-79.
- ↑ Gibney, Elizabeth (2 October 2019). "Quantum gold rush: the private funding pouring into quantum start-ups". Nature. 574 (7776): 22–24. Bibcode:2019Natur.574...22G. doi:10.1038/d41586-019-02935-4. PMID 31578480.
- ↑ Rodrigo, Chris Mills (12 February 2020). "Trump budget proposal boosts funding for artificial intelligence, quantum computing". The Hill.
{{cite news}}: CS1 maint: url-status (link) - ↑ https://www.ibm.com/blogs/research/2019/10/on-quantum-supremacy/
- ↑ Franklin, Diana; Chong, Frederic T. (2004). "Challenges in Reliable Quantum Computing". Nano, Quantum and Molecular Computing. pp. 247–266. doi:10.1007/1-4020-8068-9_8. ISBN 1-4020-8067-0.
- ↑ Pakkin, Scott; Coles, Patrick (10 June 2019). "The Problem with Quantum Computers". Scientific American.
- ↑ Nielsen, p. 29
- ↑ Lenstra, Arjen K. (2000). "Integer Factoring" (PDF). Designs, Codes and Cryptography. 19 (2/3): 101–128. doi:10.1023/A:1008397921377. Archived from the original (PDF) on 2015-04-10.
- ↑ 15.0 15.1 Bernstein, Daniel J. (2009). "Introduction to post-quantum cryptography". Post-Quantum Cryptography. 549. pp. 1–14. doi:10.1007/978-3-540-88702-7_1. ISBN 978-3-540-88701-0. PMID 28905891.
- ↑ See also pqcrypto.org, a bibliography maintained by Daniel J. Bernstein and Tanja Lange on cryptography not known to be broken by quantum computing.
- ↑ McEliece, R. J. (January 1978). "A Public-Key Cryptosystem Based On Algebraic Coding Theory" (PDF). DSNPR. 44: 114–116. Bibcode:1978DSNPR..44..114M.
- ↑ Kobayashi, H.; Gall, F.L. (2006). "Dihedral Hidden Subgroup Problem: A Survey". Information and Media Technologies. 1 (1): 178–185. doi:10.2197/ipsjdc.1.470.
- ↑ Bennett, Charles H.; Bernstein, Ethan; Brassard, Gilles; Vazirani, Umesh (October 1997). "Strengths and Weaknesses of Quantum Computing". SIAM Journal on Computing. 26 (5): 1510–1523. arXiv:quant-ph/9701001. Bibcode:1997quant.ph..1001B. doi:10.1137/s0097539796300933.
- ↑ Katwala, Amit (5 March 2020). "Quantum computers will change the world (if they work)". Wired UK.
- ↑ Ambainis, Ambainis (June 2004). "Quantum search algorithms". ACM SIGACT News. 35 (2): 22–35. arXiv:quant-ph/0504012. Bibcode:2005quant.ph..4012A. doi:10.1145/992287.992296.
- ↑ Rich, Steven; Gellman, Barton (2014-02-01). "NSA seeks to build quantum computer that could crack most types of encryption". Washington Post.
- ↑ Norton, Quinn (2007-02-15). "The Father of Quantum Computing". Wired.
- ↑ Ambainis, Andris (Spring 2014). "What Can We Do with a Quantum Computer?". Institute for Advanced Study.
- ↑ Harrow, Aram; Hassidim, Avinatan; Lloyd, Seth (2009). "Quantum algorithm for solving linear systems of equations". Physical Review Letters. 103 (15): 150502. arXiv:0811.3171. Bibcode:2009PhRvL.103o0502H. doi:10.1103/PhysRevLett.103.150502. PMID 19905613.
- ↑ Boixo, Sergio; Isakov, Sergei V.; Smelyanskiy, Vadim N.; Babbush, Ryan; Ding, Nan; Jiang, Zhang; Bremner, Michael J.; Martinis, John M.; Neven, Hartmut (2018). "Characterizing Quantum Supremacy in Near-Term Devices". Nature Physics. 14 (6): 595–600. arXiv:1608.00263. Bibcode:2018NatPh..14..595B. doi:10.1038/s41567-018-0124-x.
- ↑ Savage, Neil. "Quantum Computers Compete for "Supremacy"".
- ↑ "Quantum Supremacy and Complexity". 23 April 2016.
- ↑ Kalai, Gil. "The Quantum Computer Puzzle" (PDF). AMS.
- ↑ Arute, Frank; Arya, Kunal; Babbush, Ryan; Bacon, Dave; Bardin, Joseph C.; Barends, Rami; Biswas, Rupak; Boixo, Sergio; Brandao, Fernando G. S. L.; Buell, David A.; Burkett, Brian; Chen, Yu; Chen, Zijun; Chiaro, Ben; Collins, Roberto; Courtney, William; Dunsworsth, Andrew; Farhi, Edward; Foxen, Brooks; Fowler, Austin; Gidney, Craig; Giustina, Marissa; Graff, Rob; Guerin, Keith; Habegger, Steve; Harrigan, Matthew P.; Hartmann, Michael J.; Ho, Alan; Hoffman, Markus; Huang, Trent; Humble, Travis S.; Isakov, Sergei V.; Jeffery, Evan; Jiang, Zhang; Kafri, Dvir; Kechedzhi, Kostyantyn; Kelly, Julian; Klimov, Paul V.; Knysh, Sergey; Korotov, Alexander; Kostritsa, Fedor; Landhuis, David; Lindmark, Mike; Lucero, Erik; Lyakh, Dmitry; Mandrà, Salvatore; McClean, Jarrod R.; McEwen, Matthew; Megrant, Anthony; Mi, Xiao; Michielsen, Kristel; Mohseni, Masoud; Mutus, Josh; Naaman, Ofer; Neeley, Matthew; Neill, Charles; Niu, Murphy Yuezhen; Ostby, Eric; Petukhov, Andre; Platt, John C.; Quintana, Chris; Rieffel, Eleanor G.; Roushan, Pedram; Rubin, Nicholas C.; Sank, Daniel; Satzinger, Kevin J.; Smelyanskiy, Vadim; Sung, Kevin J.; Trevithick, Matthew D.; Vainsencher, Amit; Villalonga, Benjamin; White, Theodore; Yao, Z. Jamie; Yeh, Ping; Zalcman, Adam; Neven, Hartmut; Martinis, John M. (23 October 2019). "Quantum supremacy using a programmable superconducting processor". Nature. 574 (7779): 505–510. arXiv:1910.11333. Bibcode:2019Natur.574..505A. doi:10.1038/s41586-019-1666-5. PMID 31645734.
- ↑ "Google researchers have reportedly achieved "quantum supremacy"". MIT Technology Review.
- ↑ Unruh, Bill (1995). "Maintaining coherence in Quantum Computers". Physical Review A. 51 (2): 992–997. arXiv:hep-th/9406058. Bibcode:1995PhRvA..51..992U. doi:10.1103/PhysRevA.51.992. PMID 9911677.
- ↑ Davies, Paul. "The implications of a holographic universe for quantum information science and the nature of physical law" (PDF). Macquarie University.
- ↑ Dyakonov, Mikhail (2018-11-15). "The Case Against Quantum Computing". IEEE Spectrum.
- ↑ DiVincenzo, David P. (2000-04-13). "The Physical Implementation of Quantum Computation". Fortschritte der Physik. 48 (9–11): 771–783. arXiv:quant-ph/0002077. Bibcode:2000ForPh..48..771D. doi:10.1002/1521-3978(200009)48:9/11<771::AID-PROP771>3.0.CO;2-E.
- ↑ Giles, Martin (17 January 2019). "We'd have more quantum computers if it weren't so hard to find the damn cables". MIT Technology Review.
- ↑ DiVincenzo, David P. (1995). "Quantum Computation". Science. 270 (5234): 255–261. Bibcode:1995Sci...270..255D. CiteSeerX 10.1.1.242.2165. doi:10.1126/science.270.5234.255. (subscription required)
- ↑ Jones, Nicola (19 June 2013). "Computing: The quantum company". Nature. 498 (7454): 286–288. Bibcode:2013Natur.498..286J. doi:10.1038/498286a. PMID 23783610.
- ↑ Vepsäläinen, Antti P.; Karamlou, Amir H.; Orrell, John L.; Dogra, Akshunna S.; Loer, Ben; et al. (August 2020). "Impact of ionizing radiation on superconducting qubit coherence". Nature (in English). 584 (7822): 551–556. arXiv:2001.09190. doi:10.1038/s41586-020-2619-8. ISSN 1476-4687. PMID 32848227.
- ↑ Amy, Matthew; Matteo, Olivia; Gheorghiu, Vlad; Mosca, Michele; Parent, Alex; Schanck, John (November 30, 2016). "Estimating the cost of generic quantum pre-image attacks on SHA-2 and SHA-3". arXiv:1603.09383 [quant-ph].
- ↑ Dyakonov, M. I. (2006-10-14). S. Luryi; J. Xu; A. Zaslavsky (eds.). "Is Fault-Tolerant Quantum Computation Really Possible?". Future Trends in Microelectronics. Up the Nano Creek: 4–18. arXiv:quant-ph/0610117. Bibcode:2006quant.ph.10117D.
- ↑ Freedman, Michael H.; Kitaev, Alexei; Larsen, Michael J.; Wang, Zhenghan (2003). "Topological quantum computation". Bulletin of the American Mathematical Society. 40 (1): 31–38. arXiv:quant-ph/0101025. doi:10.1090/S0273-0979-02-00964-3. MR 1943131.
- ↑ Monroe, Don (1 October 2008). "Anyons: The breakthrough quantum computing needs?". New Scientist.
- ↑ Dyakonov, Mikhail. "The Case Against Quantum Computing". IEEE Spectrum. Retrieved 3 December 2019.
- ↑ Dyakonov, Mikhail (24 March 2020). Will We Ever Have a Quantum Computer?. Springer. ISBN 9783030420185. https://www.springer.com/gp/book/9783030420185. Retrieved 22 May 2020.
- ↑ Das, A.; Chakrabarti, B. K. (2008). "Quantum Annealing and Analog Quantum Computation". Rev. Mod. Phys. 80 (3): 1061–1081. arXiv:0801.2193. Bibcode:2008RvMP...80.1061D. CiteSeerX 10.1.1.563.9990. doi:10.1103/RevModPhys.80.1061.
- ↑ Nayak, Chetan; Simon, Steven; Stern, Ady; Das Sarma, Sankar (2008). "Nonabelian Anyons and Quantum Computation". Reviews of Modern Physics. 80 (3): 1083–1159. arXiv:0707.1889. Bibcode:2008RvMP...80.1083N. doi:10.1103/RevModPhys.80.1083.
- ↑ Clarke, John; Wilhelm, Frank K. (18 June 2008). "Superconducting quantum bits". Nature. 453 (7198): 1031–1042. Bibcode:2008Natur.453.1031C. doi:10.1038/nature07128. PMID 18563154.
- ↑ Kaminsky, William M.; Lloyd, Seth; Orlando, Terry P. (12 March 2004). "Scalable Superconducting Architecture for Adiabatic Quantum Computation". arXiv:quant-ph/0403090. Bibcode:2004quant.ph..3090K.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ Khazali, Mohammadsadegh; Mølmer, Klaus (2020-06-11). "Fast Multiqubit Gates by Adiabatic Evolution in Interacting Excited-State Manifolds of Rydberg Atoms and Superconducting Circuits". Physical Review X. 10 (2): 021054. Bibcode:2020PhRvX..10b1054K. doi:10.1103/PhysRevX.10.021054.
- ↑ Henriet, Loic; Beguin, Lucas; Signoles, Adrien; Lahaye, Thierry; Browaeys, Antoine; Reymond, Georges-Olivier; Jurczak, Christophe (2020-06-22). "Quantum computing with neutral atoms". Quantum. 4: 327. arXiv:2006.12326. doi:10.22331/q-2020-09-21-327.
- ↑ Imamog¯lu, A.; Awschalom, D. D.; Burkard, G.; DiVincenzo, D. P.; Loss, D.; Sherwin, M.; Small, A. (15 November 1999). "Quantum Information Processing Using Quantum Dot Spins and Cavity QED". Physical Review Letters. 83 (20): 4204–4207. arXiv:quant-ph/9904096. Bibcode:1999PhRvL..83.4204I. doi:10.1103/PhysRevLett.83.4204.
- ↑ Fedichkin, L.; Yanchenko, M.; Valiev, K. A. (June 2000). "Novel coherent quantum bit using spatial quantization levels in semiconductor quantum dot". Quantum Computers and Computing. 1: 58. arXiv:quant-ph/0006097. Bibcode:2000quant.ph..6097F.
- ↑ Ivády, Viktor; Davidsson, Joel; Delegan, Nazar; Falk, Abram L.; Klimov, Paul V.; Whiteley, Samuel J.; Hruszkewycz, Stephan O.; Holt, Martin V.; Heremans, F. Joseph; Son, Nguyen Tien; Awschalom, David D.; Abrikosov, Igor A.; Gali, Adam (6 December 2019). "Stabilization of point-defect spin qubits by quantum wells". Nature Communications. 10 (1): 5607. arXiv:1905.11801. Bibcode:2019NatCo..10.5607I. doi:10.1038/s41467-019-13495-6. PMC 6898666. PMID 31811137.
- ↑ "Scientists Discover New Way to Get Quantum Computing to Work at Room Temperature". interestingengineering.com. 24 April 2020.
- ↑ Bertoni, A.; Bordone, P.; Brunetti, R.; Jacoboni, C.; Reggiani, S. (19 June 2000). "Quantum Logic Gates based on Coherent Electron Transport in Quantum Wires". Physical Review Letters. 84 (25): 5912–5915. Bibcode:2000PhRvL..84.5912B. doi:10.1103/PhysRevLett.84.5912. hdl:11380/303796. PMID 10991086.
- ↑ Ionicioiu, Radu; Amaratunga, Gehan; Udrea, Florin (20 January 2001). "Quantum Computation with Ballistic Electrons". International Journal of Modern Physics B. 15 (2): 125–133. arXiv:quant-ph/0011051. Bibcode:2001IJMPB..15..125I. CiteSeerX 10.1.1.251.9617. doi:10.1142/S0217979201003521.
- ↑ Ramamoorthy, A; Bird, J P; Reno, J L (11 July 2007). "Using split-gate structures to explore the implementation of a coupled-electron-waveguide qubit scheme". Journal of Physics: Condensed Matter. 19 (27): 276205. Bibcode:2007JPCM...19A6205R. doi:10.1088/0953-8984/19/27/276205.
- ↑ Leuenberger, Michael N.; Loss, Daniel (April 2001). "Quantum computing in molecular magnets". Nature. 410 (6830): 789–793. arXiv:cond-mat/0011415. Bibcode:2001Natur.410..789L. doi:10.1038/35071024. PMID 11298441.
- ↑ Harneit, Wolfgang (27 February 2002). "Fullerene-based electron-spin quantum computer". Physical Review A. 65 (3): 032322. Bibcode:2002PhRvA..65c2322H. doi:10.1103/PhysRevA.65.032322.https://www.researchgate.net/publication/257976907_Fullerene-based_electron-spin_quantum_computer
- ↑ K. Igeta and Y. Yamamoto. "Quantum mechanical computers with single atom and photon fields." International Quantum Electronics Conference (1988) https://www.osapublishing.org/abstract.cfm?uri=IQEC-1988-TuI4
- ↑ I.L. Chuang and Y. Yamamoto. "Simple quantum computer." Physical Review A 52, 5, 3489 (1995) https://doi.org/10.1103/PhysRevA.52.3489
- ↑ Knill, G. J.; Laflamme, R.; Milburn, G. J. (2001). "A scheme for efficient quantum computation with linear optics". Nature. 409 (6816): 46–52. Bibcode:2001Natur.409...46K. doi:10.1038/35051009. PMID 11343107.
- ↑ Nizovtsev, A. P. (August 2005). "A quantum computer based on NV centers in diamond: Optically detected nutations of single electron and nuclear spins". Optics and Spectroscopy. 99 (2): 248–260. Bibcode:2005OptSp..99..233N. doi:10.1134/1.2034610.
- ↑ Dutt, M. V. G.; Childress, L.; Jiang, L.; Togan, E.; Maze, J.; Jelezko, F.; Zibrov, A. S.; Hemmer, P. R.; Lukin, M. D. (1 June 2007). "Quantum Register Based on Individual Electronic and Nuclear Spin Qubits in Diamond". Science. 316 (5829): 1312–1316. Bibcode:2007Sci...316.....D. doi:10.1126/science.1139831. PMID 17540898. Lay summary.
{{cite journal}}: Cite uses deprecated parameter|lay-url=(help) - ↑ Neumann, P.; et al. (6 June 2008). "Multipartite Entanglement Among Single Spins in Diamond". Science. 320 (5881): 1326–1329. Bibcode:2008Sci...320.1326N. doi:10.1126/science.1157233. PMID 18535240.
- ↑ Anderlini, Marco; Lee, Patricia J.; Brown, Benjamin L.; Sebby-Strabley, Jennifer; Phillips, William D.; Porto, J. V. (July 2007). "Controlled exchange interaction between pairs of neutral atoms in an optical lattice". Nature. 448 (7152): 452–456. arXiv:0708.2073. Bibcode:2007Natur.448..452A. doi:10.1038/nature06011. PMID 17653187. Lay summary.
{{cite journal}}: Cite uses deprecated parameter|lay-url=(help) - ↑ Ohlsson, N.; Mohan, R. K.; Kröll, S. (1 January 2002). "Quantum computer hardware based on rare-earth-ion-doped inorganic crystals". Opt. Commun. 201 (1–3): 71–77. Bibcode:2002OptCo.201...71O. doi:10.1016/S0030-4018(01)01666-2.
- ↑ Longdell, J. J.; Sellars, M. J.; Manson, N. B. (23 September 2004). "Demonstration of conditional quantum phase shift between ions in a solid". Phys. Rev. Lett. 93 (13): 130503. arXiv:quant-ph/0404083. Bibcode:2004PhRvL..93m0503L. doi:10.1103/PhysRevLett.93.130503. PMID 15524694.
- ↑ Náfrádi, Bálint; Choucair, Mohammad; Dinse, Klaus-Peter; Forró, László (18 July 2016). "Room temperature manipulation of long lifetime spins in metallic-like carbon nanospheres". Nature Communications. 7 (1): 12232. arXiv:1611.07690. Bibcode:2016NatCo...712232N. doi:10.1038/ncomms12232. PMC 4960311. PMID 27426851.
- ↑ Nielsen, p. 29
- ↑ Nielsen, p. 41
- ↑ Nielsen, p. 201
- ↑ Nielsen, p. 42
- ↑ 75.0 75.1 Bernstein, Ethan; Vazirani, Umesh (1997). "Quantum Complexity Theory". SIAM Journal on Computing. 26 (5): 1411–1473. CiteSeerX 10.1.1.144.7852. doi:10.1137/S0097539796300921.
- ↑ Aaronson, Scott. "Quantum Computing and Hidden Variables" (PDF).
- ↑ Aaronson, Scott (2005). "NP-complete Problems and Physical Reality". ACM SIGACT News. 2005. arXiv:quant-ph/0502072. Bibcode:2005quant.ph..2072A. See section 7 "Quantum Gravity": "[…] to anyone who wants a test or benchmark for a favorite quantum gravity theory,[author's footnote: That is, one without all the bother of making numerical predictions and comparing them to observation] let me humbly propose the following: can you define Quantum Gravity Polynomial-Time? […] until we can say what it means for a 'user' to specify an 'input' and ‘later' receive an 'output'—there is no such thing as computation, not even theoretically." (emphasis in original)
- ↑ "D-Wave Systems sells its first Quantum Computing System to Lockheed Martin Corporation". D-Wave. 25 May 2011. Retrieved 30 May 2011.
编者推荐
集智课程
量子信息基础
量子力学作为现代物理学的两大核心理论之一,成功描述了微观物理体系的演化规律,奠定了现代信息科学特别是微电子学和光电子学的物理理论基础。量子概念的引入深刻地揭示了一系列与宏观体系截然不同的物理机制,在近年来逐渐发展出了包含量子通信、量子计算、量子模拟、量子测量等量子信息科学的全新研究领域和方向。
该课程主要分为微电子学科的量子力学基础和量子信息科学基础两大部分的内容。针对新工科建设的需求,适当选用工程类量子力学教材,突出量子概念,淡化原有课程中的理论性要求较高的部分内容。适量采用Matlab编写的数值工具代替部分繁琐的公式推导。
系统科学导引(四):量子力学
本课程是《系统科学概论》课程的后续课程。《概论》是系统科学研究的入门课程。学生需要通过《概论》课程来了解什么是系统科学(系统科学的思想),以及了解一些具体的系统科学的研究方法。系统科学后续课程的目标是在此基础上,学会一些研究方法,体会一些系统科学的研究工作的实例。同时,为了给后续的课程做准备,在《概论》课程之后,专业课程之前,在本课程中,我们要学会一些数学物理的基础。
该课程主要包含两个模块:数学基础、物理学基础。其中,数学模块主要是集合与映射、矢量空间和概率论。物理模块主要是经典力学、统计力学、计算物理学初步和量子力学。
尤亦庄:Quantum Mechanics(英文-2021)
该课程引自集智科学家尤亦庄在 UCSD 开设的课堂,课程从量子比特开始谈起,逐一介绍了量子力学的五大公理(量子态,观测量,量子测量,时间演化,多体系统),循序渐进地建立量子力学的基本概念和体系。在此基础上,课程着重探讨了量子纠缠,量子测量和量子纠错等量子信息学的入门知识。
信息论
信息论(information theory)涉及信息的量化、存储和通信等。信息论是由克劳德·香农发展来的,用来找出信号处理与通信操作的基本限制,如数据压缩、可靠的存储和数据传输等。自创立以来,它已拓展应用到许多其他领域,包括统计推断、密码学、神经生物学、进化论、量子计算、剽窃检测和其他形式的数据分析。
该课程融合经典和现代信息论的成果,为信息科学方向学生提供一个统一的信息论基础,也可作为专业入门课程。主要讲解了熵,熵率,微分熵,AEP,数据压缩和信道的相关知识。
本中文词条由水流心不竞编译,Fernando审校,薄荷编辑,如有问题,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。