“非线性系统”的版本间的差异
| 第61行: | 第61行: | ||
“使用‘非线性科学’这样的术语,就如同把动物学里大部分对象称作‘非大象动物’研究一样可笑。” | “使用‘非线性科学’这样的术语,就如同把动物学里大部分对象称作‘非大象动物’研究一样可笑。” | ||
| − | + | ——斯塔尼斯拉夫·乌拉姆 | |
| 第67行: | 第67行: | ||
| − | |||
| − | ==Definition== | + | ==Definition 定义== |
| − | |||
In [[mathematics]], a [[linear map]] (or ''linear function'') <math>f(x)</math> is one which satisfies both of the following properties: | In [[mathematics]], a [[linear map]] (or ''linear function'') <math>f(x)</math> is one which satisfies both of the following properties: | ||
| 第81行: | 第79行: | ||
*Additivity or [[superposition principle]]: <math>\textstyle f(x + y) = f(x) + f(y);</math> | *Additivity or [[superposition principle]]: <math>\textstyle f(x + y) = f(x) + f(y);</math> | ||
| + | *Homogeneity: <math>\textstyle f(\alpha x) = \alpha f(x).</math> | ||
| − | |||
| − | |||
*可加性(叠加性): <math>\textstyle f(x + y) = f(x) + f(y);</math> | *可加性(叠加性): <math>\textstyle f(x + y) = f(x) + f(y);</math> | ||
| − | |||
| − | |||
*齐次性: <math>\textstyle f(\alpha x) = \alpha f(x).</math> | *齐次性: <math>\textstyle f(\alpha x) = \alpha f(x).</math> | ||
| 第111行: | 第106行: | ||
An equation written as | An equation written as | ||
| − | + | 对一个写成 | |
<math>f(x) = C</math> | <math>f(x) = C</math> | ||
| 第125行: | 第120行: | ||
is called linear if <math>f(x)</math> is a linear map (as defined above) and nonlinear otherwise. The equation is called homogeneous if <math>C = 0</math>. | is called linear if <math>f(x)</math> is a linear map (as defined above) and nonlinear otherwise. The equation is called homogeneous if <math>C = 0</math>. | ||
| − | + | 的方程,若 <math> f (x) </math> 是线性映射(如上定义) ,则称其为线性的,否则称为非线性的。若<math>C = 0</math>,该方程称为是齐次的。 | |
| 第135行: | 第130行: | ||
The definition <math>f(x) = C</math> is very general in that <math>x</math> can be any sensible mathematical object (number, vector, function, etc.), and the function <math>f(x)</math> can literally be any mapping, including integration or differentiation with associated constraints (such as boundary values). If <math>f(x)</math> contains differentiation with respect to <math>x</math>, the result will be a differential equation. | The definition <math>f(x) = C</math> is very general in that <math>x</math> can be any sensible mathematical object (number, vector, function, etc.), and the function <math>f(x)</math> can literally be any mapping, including integration or differentiation with associated constraints (such as boundary values). If <math>f(x)</math> contains differentiation with respect to <math>x</math>, the result will be a differential equation. | ||
| − | 定义 math f (x) | + | 定义 <math>f(x) = C</math> 是非常具有一般性的,因为 <math>x</math> 可以是任意可感知的数学对象(数字、向量、函数等),函数 <math>f(x)</math> 实际上可以是任意映射,包括有相关约束(如给定边界值)的积分或微分。若 <math>f(x)</math> 包含对 <math>x</math> 的微分运算,则该方程为微分方程。 |
| 第141行: | 第136行: | ||
| − | ==Nonlinear algebraic equations== | + | ==Nonlinear algebraic equations 非线性代数方程== |
| − | |||
| − | |||
| − | |||
{{Main|Algebraic equation|System of polynomial equations}} | {{Main|Algebraic equation|System of polynomial equations}} | ||
| 第155行: | 第147行: | ||
Nonlinear algebraic equations, which are also called polynomial equations, are defined by equating polynomials (of degree greater than one) to zero. For example, | Nonlinear algebraic equations, which are also called polynomial equations, are defined by equating polynomials (of degree greater than one) to zero. For example, | ||
| − | + | 非线性代数方程,又称多项式方程,由某多项式(次数大于1)等于零定义。例如: | |
| − | |||
| − | |||
<math>x^2 + x - 1 = 0\,.</math> | <math>x^2 + x - 1 = 0\,.</math> | ||
| − | |||
| − | |||
| 第171行: | 第159行: | ||
For a single polynomial equation, root-finding algorithms can be used to find solutions to the equation (i.e., sets of values for the variables that satisfy the equation). However, systems of algebraic equations are more complicated; their study is one motivation for the field of algebraic geometry, a difficult branch of modern mathematics. It is even difficult to decide whether a given algebraic system has complex solutions (see Hilbert's Nullstellensatz). Nevertheless, in the case of the systems with a finite number of complex solutions, these systems of polynomial equations are now well understood and efficient methods exist for solving them. | For a single polynomial equation, root-finding algorithms can be used to find solutions to the equation (i.e., sets of values for the variables that satisfy the equation). However, systems of algebraic equations are more complicated; their study is one motivation for the field of algebraic geometry, a difficult branch of modern mathematics. It is even difficult to decide whether a given algebraic system has complex solutions (see Hilbert's Nullstellensatz). Nevertheless, in the case of the systems with a finite number of complex solutions, these systems of polynomial equations are now well understood and efficient methods exist for solving them. | ||
| − | + | 对于一个单一的多项式方程,求根算法可用于其求解(即找到满足该方程的变量的值集)。而代数方程组则相对复杂,其研究是现代数学的较难分支——代数几何领域的动力之一。甚至很难判断一个给定的代数系统是否有复数解(见希尔伯特的零点定律)。不过,对于具有有限个复数解的系统的多项式方程组,我们现在已经有了充分的理解,并且找到了有效的求解方法。 | |
| 第177行: | 第165行: | ||
| − | ==Nonlinear recurrence relations== | + | ==Nonlinear recurrence relations 非线性递推关系== |
| − | |||
| − | |||
A nonlinear [[recurrence relation]] defines successive terms of a [[sequence]] as a nonlinear function of preceding terms. Examples of nonlinear recurrence relations are the [[logistic map]] and the relations that define the various [[Hofstadter sequence]]s. Nonlinear discrete models that represent a wide class of nonlinear recurrence relationships include the NARMAX (Nonlinear Autoregressive Moving Average with eXogenous inputs) model and the related [[nonlinear system identification]] and analysis procedures.<ref name="SAB1">Billings S.A. "Nonlinear System Identification: NARMAX Methods in the Time, Frequency, and Spatio-Temporal Domains". Wiley, 2013</ref> These approaches can be used to study a wide class of complex nonlinear behaviors in the time, frequency, and spatio-temporal domains. | A nonlinear [[recurrence relation]] defines successive terms of a [[sequence]] as a nonlinear function of preceding terms. Examples of nonlinear recurrence relations are the [[logistic map]] and the relations that define the various [[Hofstadter sequence]]s. Nonlinear discrete models that represent a wide class of nonlinear recurrence relationships include the NARMAX (Nonlinear Autoregressive Moving Average with eXogenous inputs) model and the related [[nonlinear system identification]] and analysis procedures.<ref name="SAB1">Billings S.A. "Nonlinear System Identification: NARMAX Methods in the Time, Frequency, and Spatio-Temporal Domains". Wiley, 2013</ref> These approaches can be used to study a wide class of complex nonlinear behaviors in the time, frequency, and spatio-temporal domains. | ||
| 第187行: | 第173行: | ||
A nonlinear recurrence relation defines successive terms of a sequence as a nonlinear function of preceding terms. Examples of nonlinear recurrence relations are the logistic map and the relations that define the various Hofstadter sequences. Nonlinear discrete models that represent a wide class of nonlinear recurrence relationships include the NARMAX (Nonlinear Autoregressive Moving Average with eXogenous inputs) model and the related nonlinear system identification and analysis procedures. These approaches can be used to study a wide class of complex nonlinear behaviors in the time, frequency, and spatio-temporal domains. | A nonlinear recurrence relation defines successive terms of a sequence as a nonlinear function of preceding terms. Examples of nonlinear recurrence relations are the logistic map and the relations that define the various Hofstadter sequences. Nonlinear discrete models that represent a wide class of nonlinear recurrence relationships include the NARMAX (Nonlinear Autoregressive Moving Average with eXogenous inputs) model and the related nonlinear system identification and analysis procedures. These approaches can be used to study a wide class of complex nonlinear behaviors in the time, frequency, and spatio-temporal domains. | ||
| − | + | 非线性递归关系中,序列的连续项被定义为其前项的非线性函数。非线性递归关系的例子有 logistic 映射和定义各种霍夫斯塔特序列 Hofstadter sequences 的关系。非线性离散模型代表了一类广泛的非线性递归关系,包括 NARMAX(外部输入非线性自回归移动平均)模型和相关的非线性系统辨识和分析程序。这些方法可用于研究时域、频域和时空域的广泛复杂非线性行为。 | |
| 第193行: | 第179行: | ||
| − | ==Nonlinear differential equations== | + | ==Nonlinear differential equations 非线性微分方程== |
| − | |||
| − | |||
A [[simultaneous equations|system]] of [[differential equation]]s is said to be nonlinear if it is not a [[linear system]]. Problems involving nonlinear differential equations are extremely diverse, and methods of solution or analysis are problem dependent. Examples of nonlinear differential equations are the [[Navier–Stokes equations]] in fluid dynamics and the [[Lotka–Volterra equation]]s in biology. | A [[simultaneous equations|system]] of [[differential equation]]s is said to be nonlinear if it is not a [[linear system]]. Problems involving nonlinear differential equations are extremely diverse, and methods of solution or analysis are problem dependent. Examples of nonlinear differential equations are the [[Navier–Stokes equations]] in fluid dynamics and the [[Lotka–Volterra equation]]s in biology. | ||
| 第203行: | 第187行: | ||
A system of differential equations is said to be nonlinear if it is not a linear system. Problems involving nonlinear differential equations are extremely diverse, and methods of solution or analysis are problem dependent. Examples of nonlinear differential equations are the Navier–Stokes equations in fluid dynamics and the Lotka–Volterra equations in biology. | A system of differential equations is said to be nonlinear if it is not a linear system. Problems involving nonlinear differential equations are extremely diverse, and methods of solution or analysis are problem dependent. Examples of nonlinear differential equations are the Navier–Stokes equations in fluid dynamics and the Lotka–Volterra equations in biology. | ||
| − | + | 若一个微分方程组不是线性系统,则称其为非线性的。涉及非线性微分方程的问题非常多样,对不同问题的解决或分析方法也不相同。非线性微分方程的例子有流体力学中的 纳维-斯托克斯 Navier-Stokes 方程和生物学中的洛特卡-沃尔泰拉 Lotka-Volterra 方程。 | |
| 第213行: | 第197行: | ||
One of the greatest difficulties of nonlinear problems is that it is not generally possible to combine known solutions into new solutions. In linear problems, for example, a family of linearly independent solutions can be used to construct general solutions through the superposition principle. A good example of this is one-dimensional heat transport with Dirichlet boundary conditions, the solution of which can be written as a time-dependent linear combination of sinusoids of differing frequencies; this makes solutions very flexible. It is often possible to find several very specific solutions to nonlinear equations, however the lack of a superposition principle prevents the construction of new solutions. | One of the greatest difficulties of nonlinear problems is that it is not generally possible to combine known solutions into new solutions. In linear problems, for example, a family of linearly independent solutions can be used to construct general solutions through the superposition principle. A good example of this is one-dimensional heat transport with Dirichlet boundary conditions, the solution of which can be written as a time-dependent linear combination of sinusoids of differing frequencies; this makes solutions very flexible. It is often possible to find several very specific solutions to nonlinear equations, however the lack of a superposition principle prevents the construction of new solutions. | ||
| − | + | 非线性问题最大的困难之一是通常不可能将已知的解组合成新的解。例如,在线性问题中,可以根据叠加原理以一族线性独立的解构造通解。一个很好的例子是带有狄利克雷 Dirichlet 边界条件的一维热传导问题,其解(随时间变化)可以写成不同频率的正弦波的线性组合,这使得解非常灵活。而对非线性方程,通常可以找到几个非常特殊的解,但是此时叠加原理不适用,故无法构造新的解。 | |
| 第219行: | 第203行: | ||
| − | ===Ordinary differential equations=== | + | ===Ordinary differential equations 常微分方程=== |
| − | |||
| − | |||
| − | |||
| − | |||
First order [[ordinary differential equation]]s are often exactly solvable by [[separation of variables]], especially for autonomous equations. For example, the nonlinear equation | First order [[ordinary differential equation]]s are often exactly solvable by [[separation of variables]], especially for autonomous equations. For example, the nonlinear equation | ||
| 第229行: | 第209行: | ||
First order ordinary differential equations are often exactly solvable by separation of variables, especially for autonomous equations. For example, the nonlinear equation | First order ordinary differential equations are often exactly solvable by separation of variables, especially for autonomous equations. For example, the nonlinear equation | ||
| − | + | 一阶常微分方程,尤其是自治方程,通常可以用分离变量法来精确求解。例如,非线性方程 | |
| − | |||
| − | |||
<math>\frac{d u}{d x} = -u^2</math> | <math>\frac{d u}{d x} = -u^2</math> | ||
| − | |||
| − | |||
| 第245行: | 第221行: | ||
has <math>u=\frac{1}{x+C}</math> as a general solution (and also u = 0 as a particular solution, corresponding to the limit of the general solution when C tends to infinity). The equation is nonlinear because it may be written as | has <math>u=\frac{1}{x+C}</math> as a general solution (and also u = 0 as a particular solution, corresponding to the limit of the general solution when C tends to infinity). The equation is nonlinear because it may be written as | ||
| − | 将 | + | 将 <math>u=\frac{1}{x+C}</math> 作为一般解(也有特解 ''u'' = 0,对应于 ''C'' 趋于无穷时的一般解的极限)。该方程是非线性的,因为它可以改写成 |
| − | |||
| − | |||
<math>\frac{du}{d x} + u^2=0</math> | <math>\frac{du}{d x} + u^2=0</math> | ||
| − | |||
| 第261行: | 第234行: | ||
and the left-hand side of the equation is not a linear function of u and its derivatives. Note that if the u<sup>2</sup> term were replaced with u, the problem would be linear (the exponential decay problem). | and the left-hand side of the equation is not a linear function of u and its derivatives. Note that if the u<sup>2</sup> term were replaced with u, the problem would be linear (the exponential decay problem). | ||
| − | 方程的左边不是 u | + | 方程的左边不是 ''u'' 及其导数的线性函数。注意,若将 ''u''<sup>2</sup> 项替换为''u'',该问题将变为线性的(指数衰减问题)。 |
| 第271行: | 第244行: | ||
Second and higher order ordinary differential equations (more generally, systems of nonlinear equations) rarely yield closed-form solutions, though implicit solutions and solutions involving nonelementary integrals are encountered. | Second and higher order ordinary differential equations (more generally, systems of nonlinear equations) rarely yield closed-form solutions, though implicit solutions and solutions involving nonelementary integrals are encountered. | ||
| − | + | 二阶和高阶常微分方程(更一般地说,非线性方程组)很少能产生封闭解,而隐式解和非初等函数积分形式的解较为常见。 | |
| 第289行: | 第262行: | ||
*Examination of any [[conserved quantities]], especially in [[Hamiltonian system]]s | *Examination of any [[conserved quantities]], especially in [[Hamiltonian system]]s | ||
| − | + | *检查是否有任意守恒量(特别是在哈密顿系统中) | |
*Examination of dissipative quantities (see [[Lyapunov function]]) analogous to conserved quantities | *Examination of dissipative quantities (see [[Lyapunov function]]) analogous to conserved quantities | ||
| − | + | *检查是否有类似守恒量的耗散量(见李亚普诺夫函数) | |
*Linearization via [[Taylor expansion]] | *Linearization via [[Taylor expansion]] | ||
| − | + | *基于泰勒展开的线性化 | |
*Change of variables into something easier to study | *Change of variables into something easier to study | ||
| − | + | *将变量转化得更易于研究 | |
*[[Bifurcation theory]] | *[[Bifurcation theory]] | ||
| − | + | *分岔理论 | |
*[[Perturbation theory|Perturbation]] methods (can be applied to algebraic equations too) | *[[Perturbation theory|Perturbation]] methods (can be applied to algebraic equations too) | ||
| + | *摄动理论(也可应用于代数方程) | ||
| 第314行: | 第288行: | ||
| + | ===Partial differential equations 偏微分方程=== | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{{main|Nonlinear partial differential equation}} | {{main|Nonlinear partial differential equation}} | ||
| 第327行: | 第297行: | ||
{{See also|List of nonlinear partial differential equations}} | {{See also|List of nonlinear partial differential equations}} | ||
| − | + | 参见:非线性偏微分列表 | |
The most common basic approach to studying nonlinear [[partial differential equation]]s is to change the variables (or otherwise transform the problem) so that the resulting problem is simpler (possibly even linear). Sometimes, the equation may be transformed into one or more [[ordinary differential equation]]s, as seen in [[separation of variables]], which is always useful whether or not the resulting ordinary differential equation(s) is solvable. | The most common basic approach to studying nonlinear [[partial differential equation]]s is to change the variables (or otherwise transform the problem) so that the resulting problem is simpler (possibly even linear). Sometimes, the equation may be transformed into one or more [[ordinary differential equation]]s, as seen in [[separation of variables]], which is always useful whether or not the resulting ordinary differential equation(s) is solvable. | ||
| 第333行: | 第303行: | ||
The most common basic approach to studying nonlinear partial differential equations is to change the variables (or otherwise transform the problem) so that the resulting problem is simpler (possibly even linear). Sometimes, the equation may be transformed into one or more ordinary differential equations, as seen in separation of variables, which is always useful whether or not the resulting ordinary differential equation(s) is solvable. | The most common basic approach to studying nonlinear partial differential equations is to change the variables (or otherwise transform the problem) so that the resulting problem is simpler (possibly even linear). Sometimes, the equation may be transformed into one or more ordinary differential equations, as seen in separation of variables, which is always useful whether or not the resulting ordinary differential equation(s) is solvable. | ||
| − | + | 研究非线性偏微分方程最常用的基本方法是变换变量(或转换问题),使变换后的问题更简单(甚至可能变为线性的)。有时可以将此类方程转化成一或多个常微分方程(如同分离变量法所示),此时不论得到的常微分方程是否可解,对研究问题总是有用的。 | |
| 第343行: | 第313行: | ||
Another common (though less mathematic) tactic, often seen in fluid and heat mechanics, is to use scale analysis to simplify a general, natural equation in a certain specific boundary value problem. For example, the (very) nonlinear Navier-Stokes equations can be simplified into one linear partial differential equation in the case of transient, laminar, one dimensional flow in a circular pipe; the scale analysis provides conditions under which the flow is laminar and one dimensional and also yields the simplified equation. | Another common (though less mathematic) tactic, often seen in fluid and heat mechanics, is to use scale analysis to simplify a general, natural equation in a certain specific boundary value problem. For example, the (very) nonlinear Navier-Stokes equations can be simplified into one linear partial differential equation in the case of transient, laminar, one dimensional flow in a circular pipe; the scale analysis provides conditions under which the flow is laminar and one dimensional and also yields the simplified equation. | ||
| − | + | 另一个流体力学和热力学中常见的策略(虽然不是数学上的)是利用尺度分析来在某一特定边界条件下简化一般自然方程。例如,在描述圆管内一维层流的暂态时,非线性的纳维-斯托克斯方程可以简化为一个线性的偏微分方程; 尺度分析提供了层流和一维流动的条件,也产生了简化的方程。 | |
| 第353行: | 第323行: | ||
Other methods include examining the characteristics and using the methods outlined above for ordinary differential equations. | Other methods include examining the characteristics and using the methods outlined above for ordinary differential equations. | ||
| − | + | 其他方法包括检查特征线法及前面所述研究常微分方程的方法。 | |
| − | |||
| − | |||
| − | ===Pendula=== | + | ===Pendula 摆=== |
| − | |||
{{Main|Pendulum (mathematics)}} | {{Main|Pendulum (mathematics)}} | ||
| 第373行: | 第340行: | ||
| − | [[File:PendulumLayout.svg | + | [[File:PendulumLayout.svg.png|thumb|Illustration of a pendulum 摆图解|right|200px]] |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | 200px | + | [[File:PendulumLinearizations.png|thumb|Linearizations of a pendulum 摆的线性化|right|200px]] |
| 第393行: | 第353行: | ||
A classic, extensively studied nonlinear problem is the dynamics of a pendulum under the influence of gravity. Using Lagrangian mechanics, it may be shown that the motion of a pendulum can be described by the dimensionless nonlinear equation | A classic, extensively studied nonlinear problem is the dynamics of a pendulum under the influence of gravity. Using Lagrangian mechanics, it may be shown that the motion of a pendulum can be described by the dimensionless nonlinear equation | ||
| − | + | 一个经典的被广泛研究的非线性问题是重力影响下的摆的动力学。利用拉格朗日力学,可以证明摆的运动可以用无量纲的非线性方程 | |
| − | |||
| − | |||
<math>\frac{d^2 \theta}{d t^2} + \sin(\theta) = 0</math> | <math>\frac{d^2 \theta}{d t^2} + \sin(\theta) = 0</math> | ||
| − | |||
| − | |||
| 第409行: | 第365行: | ||
where gravity points "downwards" and <math>\theta</math> is the angle the pendulum forms with its rest position, as shown in the figure at right. One approach to "solving" this equation is to use <math>d\theta/dt</math> as an integrating factor, which would eventually yield | where gravity points "downwards" and <math>\theta</math> is the angle the pendulum forms with its rest position, as shown in the figure at right. One approach to "solving" this equation is to use <math>d\theta/dt</math> as an integrating factor, which would eventually yield | ||
| − | + | 描述,其中重力指向“下方”,<math>\theta</math> 是摆与其静止位置形成的角度,如右图所示。“解”这个方程的方法之一是用 <math>d\theta/dt</math> 作为积分因子,最终得 | |
| − | |||
| − | |||
<math>\int{\frac{d \theta}{\sqrt{C_0 + 2 \cos(\theta)}}} = t + C_1</math> | <math>\int{\frac{d \theta}{\sqrt{C_0 + 2 \cos(\theta)}}} = t + C_1</math> | ||
| − | |||
| − | |||
| 第425行: | 第377行: | ||
which is an implicit solution involving an elliptic integral. This "solution" generally does not have many uses because most of the nature of the solution is hidden in the nonelementary integral (nonelementary unless <math>C_0 = 2</math>). | which is an implicit solution involving an elliptic integral. This "solution" generally does not have many uses because most of the nature of the solution is hidden in the nonelementary integral (nonelementary unless <math>C_0 = 2</math>). | ||
| − | + | 这是一个含椭圆积分的隐式解。这个“解”通常没什么用,因为这个解的大部分性质都隐藏在非初等函数积分中(除非<math>C_0 = 2</math>,否则是非初等的)。 | |
| 第435行: | 第387行: | ||
Another way to approach the problem is to linearize any nonlinearities (the sine function term in this case) at the various points of interest through Taylor expansions. For example, the linearization at <math>\theta = 0</math>, called the small angle approximation, is | Another way to approach the problem is to linearize any nonlinearities (the sine function term in this case) at the various points of interest through Taylor expansions. For example, the linearization at <math>\theta = 0</math>, called the small angle approximation, is | ||
| − | + | 另一种解决这个问题的方法是利用泰勒展开将任意非线性项(此时为正弦函数项)在某些感兴趣的点线性化。例如,在<math>\theta = 0</math> 的点附近线性化(称为小角度近似)为 | |
| − | |||
| − | |||
<math>\frac{d^2 \theta}{d t^2} + \theta = 0</math> | <math>\frac{d^2 \theta}{d t^2} + \theta = 0</math> | ||
| − | |||
| − | |||
| 第451行: | 第399行: | ||
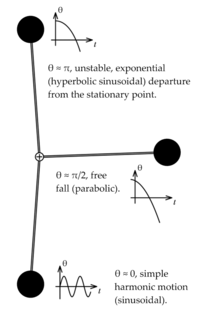
since <math>\sin(\theta) \approx \theta</math> for <math>\theta \approx 0</math>. This is a simple harmonic oscillator corresponding to oscillations of the pendulum near the bottom of its path. Another linearization would be at <math>\theta = \pi</math>, corresponding to the pendulum being straight up: | since <math>\sin(\theta) \approx \theta</math> for <math>\theta \approx 0</math>. This is a simple harmonic oscillator corresponding to oscillations of the pendulum near the bottom of its path. Another linearization would be at <math>\theta = \pi</math>, corresponding to the pendulum being straight up: | ||
| − | + | 因为 <math>\theta \approx 0</math> 时,有 <math>\sin(\theta) \approx \theta</math>。这是一个简谐振子,对应于摆在其路径底部附近的摆动。另一种线性化方法是在 <math>\theta = \pi</math>附近线性化,对应于运动到最高点的摆: | |
| − | |||
| − | |||
<math>\frac{d^2 \theta}{d t^2} + \pi - \theta = 0</math> | <math>\frac{d^2 \theta}{d t^2} + \pi - \theta = 0</math> | ||
| − | |||
| − | |||
| 第467行: | 第411行: | ||
since <math>\sin(\theta) \approx \pi - \theta</math> for <math>\theta \approx \pi</math>. The solution to this problem involves hyperbolic sinusoids, and note that unlike the small angle approximation, this approximation is unstable, meaning that <math>|\theta|</math> will usually grow without limit, though bounded solutions are possible. This corresponds to the difficulty of balancing a pendulum upright, it is literally an unstable state. | since <math>\sin(\theta) \approx \pi - \theta</math> for <math>\theta \approx \pi</math>. The solution to this problem involves hyperbolic sinusoids, and note that unlike the small angle approximation, this approximation is unstable, meaning that <math>|\theta|</math> will usually grow without limit, though bounded solutions are possible. This corresponds to the difficulty of balancing a pendulum upright, it is literally an unstable state. | ||
| − | + | 因为 <math>\theta \approx \pi</math> 时,有 <math>\sin(\theta) \approx \pi - \theta</math>。这个问题的解含双曲正弦曲线;注意到不同于小角度近似,它是不稳定的,这意味着 <math>|\theta|</math> 通常会无限增长,尽管有界解是可能的。这相当于平衡一个直立的钟摆的难度,它实际上是一种不稳定的状态。 | |
2020年7月9日 (四) 23:37的版本
此词条暂由彩云小译翻译,未经人工整理和审校,带来阅读不便,请见谅。
 |
| Complex systems |
|---|
| Topics |
In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input.[1][2] Nonlinear problems are of interest to engineers, biologists,[3][4][5] physicists,[6][7] mathematicians, and many other scientists because most systems are inherently nonlinear in nature.[8] Nonlinear dynamical systems, describing changes in variables over time, may appear chaotic, unpredictable, or counterintuitive, contrasting with much simpler linear systems.
In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other scientists because most systems are inherently nonlinear in nature. Nonlinear dynamical systems, describing changes in variables over time, may appear chaotic, unpredictable, or counterintuitive, contrasting with much simpler linear systems.
在数学及科学中,非线性系统是一种输出的变化与输入的变化不成比例的系统。大多数系统在本质上是非线性的,因而非线性问题引起了工程师、生物学家、物理学家、数学家和许多其他科学家的兴趣。描述变量随时间变化的非线性动力系统与较之简单得多的线性系统相比,可能显得混沌、不可预测或违反直觉。
Typically, the behavior of a nonlinear system is described in mathematics by a nonlinear system of equations, which is a set of simultaneous equations in which the unknowns (or the unknown functions in the case of differential equations) appear as variables of a polynomial of degree higher than one or in the argument of a function which is not a polynomial of degree one.
Typically, the behavior of a nonlinear system is described in mathematics by a nonlinear system of equations, which is a set of simultaneous equations in which the unknowns (or the unknown functions in the case of differential equations) appear as variables of a polynomial of degree higher than one or in the argument of a function which is not a polynomial of degree one.
通常,非线性系统的行为在数学上是由一组非线性联立方程来描述的,其中未知数(或微分方程中的未知函数)作为一个高于一次的多项式的变量出现,或者作为一个不是一次多项式的函数的论元出现。
In other words, in a nonlinear system of equations, the equation(s) to be solved cannot be written as a linear combination of the unknown variables or functions that appear in them. Systems can be defined as nonlinear, regardless of whether known linear functions appear in the equations. In particular, a differential equation is linear if it is linear in terms of the unknown function and its derivatives, even if nonlinear in terms of the other variables appearing in it.
In other words, in a nonlinear system of equations, the equation(s) to be solved cannot be written as a linear combination of the unknown variables or functions that appear in them. Systems can be defined as nonlinear, regardless of whether known linear functions appear in the equations. In particular, a differential equation is linear if it is linear in terms of the unknown function and its derivatives, even if nonlinear in terms of the other variables appearing in it.
换句话说,在非线性方程系统中,要求解的方程不能被写成未知变量或函数的线性组合。无论方程中是否有已知的线性函数,系统都可以被定义为非线性。特别是,如果一个微分方程的未知函数及其导数是线性的,即使其他变量是非线性的,也称其是线性的。
As nonlinear dynamical equations are difficult to solve, nonlinear systems are commonly approximated by linear equations (linearization). This works well up to some accuracy and some range for the input values, but some interesting phenomena such as solitons, chaos,[9] and singularities are hidden by linearization. It follows that some aspects of the dynamic behavior of a nonlinear system can appear to be counterintuitive, unpredictable or even chaotic. Although such chaotic behavior may resemble random behavior, it is in fact not random. For example, some aspects of the weather are seen to be chaotic, where simple changes in one part of the system produce complex effects throughout. This nonlinearity is one of the reasons why accurate long-term forecasts are impossible with current technology.
As nonlinear dynamical equations are difficult to solve, nonlinear systems are commonly approximated by linear equations (linearization). This works well up to some accuracy and some range for the input values, but some interesting phenomena such as solitons, chaos, and singularities are hidden by linearization. It follows that some aspects of the dynamic behavior of a nonlinear system can appear to be counterintuitive, unpredictable or even chaotic. Although such chaotic behavior may resemble random behavior, it is in fact not random. For example, some aspects of the weather are seen to be chaotic, where simple changes in one part of the system produce complex effects throughout. This nonlinearity is one of the reasons why accurate long-term forecasts are impossible with current technology.
由于非线性动力学方程难以求解,通常用线性化方程来近似非线性系统(线性化)。这种方法在一定的精度和范围对输入值效果很好,但一些有趣的现象如孤子、混沌和奇异性在线性化后被隐藏。因此,非线性系统的动态行为在某些方面可能看起来违反直觉、不可预测,甚至混沌。尽管这种混沌行为可能感觉很像随机行为,但它实际上并不是随机的。例如,天气的某些方面被认为是混沌的,其系统某部分的微小扰动就会产生复杂的影响。这种非线性是目前技术无法进行精确长期预测的原因之一。
Some authors use the term nonlinear science for the study of nonlinear systems. This term is disputed by others:
Some authors use the term nonlinear science for the study of nonlinear systems. This term is disputed by others:
有些作者用非线性科学这一术语来研究非线性系统。这一术语引起了其他人的争议:
/* Styling for Template:Quote */ .templatequote { overflow: hidden; margin: 1em 0; padding: 0 40px; } .templatequote .templatequotecite {
line-height: 1.5em; /* @noflip */ text-align: left; /* @noflip */ padding-left: 1.6em; margin-top: 0;
}
“使用‘非线性科学’这样的术语,就如同把动物学里大部分对象称作‘非大象动物’研究一样可笑。”
——斯塔尼斯拉夫·乌拉姆
Definition 定义
In mathematics, a linear map (or linear function) [math]\displaystyle{ f(x) }[/math] is one which satisfies both of the following properties:
In mathematics, a linear map (or linear function) [math]\displaystyle{ f(x) }[/math] is one which satisfies both of the following properties:
在数学中,线性映射(或线性函数)的数学[math]\displaystyle{ f (x) }[/math]满足以下两个性质:
- Additivity or superposition principle: [math]\displaystyle{ \textstyle f(x + y) = f(x) + f(y); }[/math]
- Homogeneity: [math]\displaystyle{ \textstyle f(\alpha x) = \alpha f(x). }[/math]
- 可加性(叠加性): [math]\displaystyle{ \textstyle f(x + y) = f(x) + f(y); }[/math]
- 齐次性: [math]\displaystyle{ \textstyle f(\alpha x) = \alpha f(x). }[/math]
Additivity implies homogeneity for any rational α, and, for continuous functions, for any real α. For a complex α, homogeneity does not follow from additivity. For example, an antilinear map is additive but not homogeneous. The conditions of additivity and homogeneity are often combined in the superposition principle
Additivity implies homogeneity for any rational α, and, for continuous functions, for any real α. For a complex α, homogeneity does not follow from additivity. For example, an antilinear map is additive but not homogeneous. The conditions of additivity and homogeneity are often combined in the superposition principle:
α是有理数,或α是实数且[math]\displaystyle{ f(x) }[/math]是连续函数时,由可加性可以推出齐次性。但当α是复数时,可加性不能导出齐次性。例如,反线性映射是可加的,但不是齐次的。可加性和齐次性条件经常组合,称为叠加原理:
[math]\displaystyle{ f(\alpha x + \beta y) = \alpha f(x) + \beta f(y) }[/math]
An equation written as
对一个写成
[math]\displaystyle{ f(x) = C }[/math]
is called linear if [math]\displaystyle{ f(x) }[/math] is a linear map (as defined above) and nonlinear otherwise. The equation is called homogeneous if [math]\displaystyle{ C = 0 }[/math].
is called linear if [math]\displaystyle{ f(x) }[/math] is a linear map (as defined above) and nonlinear otherwise. The equation is called homogeneous if [math]\displaystyle{ C = 0 }[/math].
的方程,若 [math]\displaystyle{ f (x) }[/math] 是线性映射(如上定义) ,则称其为线性的,否则称为非线性的。若[math]\displaystyle{ C = 0 }[/math],该方程称为是齐次的。
The definition [math]\displaystyle{ f(x) = C }[/math] is very general in that [math]\displaystyle{ x }[/math] can be any sensible mathematical object (number, vector, function, etc.), and the function [math]\displaystyle{ f(x) }[/math] can literally be any mapping, including integration or differentiation with associated constraints (such as boundary values). If [math]\displaystyle{ f(x) }[/math] contains differentiation with respect to [math]\displaystyle{ x }[/math], the result will be a differential equation.
The definition [math]\displaystyle{ f(x) = C }[/math] is very general in that [math]\displaystyle{ x }[/math] can be any sensible mathematical object (number, vector, function, etc.), and the function [math]\displaystyle{ f(x) }[/math] can literally be any mapping, including integration or differentiation with associated constraints (such as boundary values). If [math]\displaystyle{ f(x) }[/math] contains differentiation with respect to [math]\displaystyle{ x }[/math], the result will be a differential equation.
定义 [math]\displaystyle{ f(x) = C }[/math] 是非常具有一般性的,因为 [math]\displaystyle{ x }[/math] 可以是任意可感知的数学对象(数字、向量、函数等),函数 [math]\displaystyle{ f(x) }[/math] 实际上可以是任意映射,包括有相关约束(如给定边界值)的积分或微分。若 [math]\displaystyle{ f(x) }[/math] 包含对 [math]\displaystyle{ x }[/math] 的微分运算,则该方程为微分方程。
Nonlinear algebraic equations 非线性代数方程
Nonlinear algebraic equations, which are also called polynomial equations, are defined by equating polynomials (of degree greater than one) to zero. For example,
Nonlinear algebraic equations, which are also called polynomial equations, are defined by equating polynomials (of degree greater than one) to zero. For example,
非线性代数方程,又称多项式方程,由某多项式(次数大于1)等于零定义。例如:
[math]\displaystyle{ x^2 + x - 1 = 0\,. }[/math]
For a single polynomial equation, root-finding algorithms can be used to find solutions to the equation (i.e., sets of values for the variables that satisfy the equation). However, systems of algebraic equations are more complicated; their study is one motivation for the field of algebraic geometry, a difficult branch of modern mathematics. It is even difficult to decide whether a given algebraic system has complex solutions (see Hilbert's Nullstellensatz). Nevertheless, in the case of the systems with a finite number of complex solutions, these systems of polynomial equations are now well understood and efficient methods exist for solving them.[10]
For a single polynomial equation, root-finding algorithms can be used to find solutions to the equation (i.e., sets of values for the variables that satisfy the equation). However, systems of algebraic equations are more complicated; their study is one motivation for the field of algebraic geometry, a difficult branch of modern mathematics. It is even difficult to decide whether a given algebraic system has complex solutions (see Hilbert's Nullstellensatz). Nevertheless, in the case of the systems with a finite number of complex solutions, these systems of polynomial equations are now well understood and efficient methods exist for solving them.
对于一个单一的多项式方程,求根算法可用于其求解(即找到满足该方程的变量的值集)。而代数方程组则相对复杂,其研究是现代数学的较难分支——代数几何领域的动力之一。甚至很难判断一个给定的代数系统是否有复数解(见希尔伯特的零点定律)。不过,对于具有有限个复数解的系统的多项式方程组,我们现在已经有了充分的理解,并且找到了有效的求解方法。
Nonlinear recurrence relations 非线性递推关系
A nonlinear recurrence relation defines successive terms of a sequence as a nonlinear function of preceding terms. Examples of nonlinear recurrence relations are the logistic map and the relations that define the various Hofstadter sequences. Nonlinear discrete models that represent a wide class of nonlinear recurrence relationships include the NARMAX (Nonlinear Autoregressive Moving Average with eXogenous inputs) model and the related nonlinear system identification and analysis procedures.[11] These approaches can be used to study a wide class of complex nonlinear behaviors in the time, frequency, and spatio-temporal domains.
A nonlinear recurrence relation defines successive terms of a sequence as a nonlinear function of preceding terms. Examples of nonlinear recurrence relations are the logistic map and the relations that define the various Hofstadter sequences. Nonlinear discrete models that represent a wide class of nonlinear recurrence relationships include the NARMAX (Nonlinear Autoregressive Moving Average with eXogenous inputs) model and the related nonlinear system identification and analysis procedures. These approaches can be used to study a wide class of complex nonlinear behaviors in the time, frequency, and spatio-temporal domains.
非线性递归关系中,序列的连续项被定义为其前项的非线性函数。非线性递归关系的例子有 logistic 映射和定义各种霍夫斯塔特序列 Hofstadter sequences 的关系。非线性离散模型代表了一类广泛的非线性递归关系,包括 NARMAX(外部输入非线性自回归移动平均)模型和相关的非线性系统辨识和分析程序。这些方法可用于研究时域、频域和时空域的广泛复杂非线性行为。
Nonlinear differential equations 非线性微分方程
A system of differential equations is said to be nonlinear if it is not a linear system. Problems involving nonlinear differential equations are extremely diverse, and methods of solution or analysis are problem dependent. Examples of nonlinear differential equations are the Navier–Stokes equations in fluid dynamics and the Lotka–Volterra equations in biology.
A system of differential equations is said to be nonlinear if it is not a linear system. Problems involving nonlinear differential equations are extremely diverse, and methods of solution or analysis are problem dependent. Examples of nonlinear differential equations are the Navier–Stokes equations in fluid dynamics and the Lotka–Volterra equations in biology.
若一个微分方程组不是线性系统,则称其为非线性的。涉及非线性微分方程的问题非常多样,对不同问题的解决或分析方法也不相同。非线性微分方程的例子有流体力学中的 纳维-斯托克斯 Navier-Stokes 方程和生物学中的洛特卡-沃尔泰拉 Lotka-Volterra 方程。
One of the greatest difficulties of nonlinear problems is that it is not generally possible to combine known solutions into new solutions. In linear problems, for example, a family of linearly independent solutions can be used to construct general solutions through the superposition principle. A good example of this is one-dimensional heat transport with Dirichlet boundary conditions, the solution of which can be written as a time-dependent linear combination of sinusoids of differing frequencies; this makes solutions very flexible. It is often possible to find several very specific solutions to nonlinear equations, however the lack of a superposition principle prevents the construction of new solutions.
One of the greatest difficulties of nonlinear problems is that it is not generally possible to combine known solutions into new solutions. In linear problems, for example, a family of linearly independent solutions can be used to construct general solutions through the superposition principle. A good example of this is one-dimensional heat transport with Dirichlet boundary conditions, the solution of which can be written as a time-dependent linear combination of sinusoids of differing frequencies; this makes solutions very flexible. It is often possible to find several very specific solutions to nonlinear equations, however the lack of a superposition principle prevents the construction of new solutions.
非线性问题最大的困难之一是通常不可能将已知的解组合成新的解。例如,在线性问题中,可以根据叠加原理以一族线性独立的解构造通解。一个很好的例子是带有狄利克雷 Dirichlet 边界条件的一维热传导问题,其解(随时间变化)可以写成不同频率的正弦波的线性组合,这使得解非常灵活。而对非线性方程,通常可以找到几个非常特殊的解,但是此时叠加原理不适用,故无法构造新的解。
Ordinary differential equations 常微分方程
First order ordinary differential equations are often exactly solvable by separation of variables, especially for autonomous equations. For example, the nonlinear equation
First order ordinary differential equations are often exactly solvable by separation of variables, especially for autonomous equations. For example, the nonlinear equation
一阶常微分方程,尤其是自治方程,通常可以用分离变量法来精确求解。例如,非线性方程
[math]\displaystyle{ \frac{d u}{d x} = -u^2 }[/math]
has [math]\displaystyle{ u=\frac{1}{x+C} }[/math] as a general solution (and also u = 0 as a particular solution, corresponding to the limit of the general solution when C tends to infinity). The equation is nonlinear because it may be written as
has [math]\displaystyle{ u=\frac{1}{x+C} }[/math] as a general solution (and also u = 0 as a particular solution, corresponding to the limit of the general solution when C tends to infinity). The equation is nonlinear because it may be written as
将 [math]\displaystyle{ u=\frac{1}{x+C} }[/math] 作为一般解(也有特解 u = 0,对应于 C 趋于无穷时的一般解的极限)。该方程是非线性的,因为它可以改写成
[math]\displaystyle{ \frac{du}{d x} + u^2=0 }[/math]
and the left-hand side of the equation is not a linear function of u and its derivatives. Note that if the u2 term were replaced with u, the problem would be linear (the exponential decay problem).
and the left-hand side of the equation is not a linear function of u and its derivatives. Note that if the u2 term were replaced with u, the problem would be linear (the exponential decay problem).
方程的左边不是 u 及其导数的线性函数。注意,若将 u2 项替换为u,该问题将变为线性的(指数衰减问题)。
Second and higher order ordinary differential equations (more generally, systems of nonlinear equations) rarely yield closed-form solutions, though implicit solutions and solutions involving nonelementary integrals are encountered.
Second and higher order ordinary differential equations (more generally, systems of nonlinear equations) rarely yield closed-form solutions, though implicit solutions and solutions involving nonelementary integrals are encountered.
二阶和高阶常微分方程(更一般地说,非线性方程组)很少能产生封闭解,而隐式解和非初等函数积分形式的解较为常见。
Common methods for the qualitative analysis of nonlinear ordinary differential equations include:
Common methods for the qualitative analysis of nonlinear ordinary differential equations include:
非线性常微分方程定性分析的常用方法包括:
- Examination of any conserved quantities, especially in Hamiltonian systems
- 检查是否有任意守恒量(特别是在哈密顿系统中)
- Examination of dissipative quantities (see Lyapunov function) analogous to conserved quantities
- 检查是否有类似守恒量的耗散量(见李亚普诺夫函数)
- Linearization via Taylor expansion
- 基于泰勒展开的线性化
- Change of variables into something easier to study
- 将变量转化得更易于研究
- 分岔理论
- Perturbation methods (can be applied to algebraic equations too)
- 摄动理论(也可应用于代数方程)
Partial differential equations 偏微分方程
参见:非线性偏微分列表
The most common basic approach to studying nonlinear partial differential equations is to change the variables (or otherwise transform the problem) so that the resulting problem is simpler (possibly even linear). Sometimes, the equation may be transformed into one or more ordinary differential equations, as seen in separation of variables, which is always useful whether or not the resulting ordinary differential equation(s) is solvable.
The most common basic approach to studying nonlinear partial differential equations is to change the variables (or otherwise transform the problem) so that the resulting problem is simpler (possibly even linear). Sometimes, the equation may be transformed into one or more ordinary differential equations, as seen in separation of variables, which is always useful whether or not the resulting ordinary differential equation(s) is solvable.
研究非线性偏微分方程最常用的基本方法是变换变量(或转换问题),使变换后的问题更简单(甚至可能变为线性的)。有时可以将此类方程转化成一或多个常微分方程(如同分离变量法所示),此时不论得到的常微分方程是否可解,对研究问题总是有用的。
Another common (though less mathematic) tactic, often seen in fluid and heat mechanics, is to use scale analysis to simplify a general, natural equation in a certain specific boundary value problem. For example, the (very) nonlinear Navier-Stokes equations can be simplified into one linear partial differential equation in the case of transient, laminar, one dimensional flow in a circular pipe; the scale analysis provides conditions under which the flow is laminar and one dimensional and also yields the simplified equation.
Another common (though less mathematic) tactic, often seen in fluid and heat mechanics, is to use scale analysis to simplify a general, natural equation in a certain specific boundary value problem. For example, the (very) nonlinear Navier-Stokes equations can be simplified into one linear partial differential equation in the case of transient, laminar, one dimensional flow in a circular pipe; the scale analysis provides conditions under which the flow is laminar and one dimensional and also yields the simplified equation.
另一个流体力学和热力学中常见的策略(虽然不是数学上的)是利用尺度分析来在某一特定边界条件下简化一般自然方程。例如,在描述圆管内一维层流的暂态时,非线性的纳维-斯托克斯方程可以简化为一个线性的偏微分方程; 尺度分析提供了层流和一维流动的条件,也产生了简化的方程。
Other methods include examining the characteristics and using the methods outlined above for ordinary differential equations.
Other methods include examining the characteristics and using the methods outlined above for ordinary differential equations.
其他方法包括检查特征线法及前面所述研究常微分方程的方法。
Pendula 摆
A classic, extensively studied nonlinear problem is the dynamics of a pendulum under the influence of gravity. Using Lagrangian mechanics, it may be shown[12] that the motion of a pendulum can be described by the dimensionless nonlinear equation
A classic, extensively studied nonlinear problem is the dynamics of a pendulum under the influence of gravity. Using Lagrangian mechanics, it may be shown that the motion of a pendulum can be described by the dimensionless nonlinear equation
一个经典的被广泛研究的非线性问题是重力影响下的摆的动力学。利用拉格朗日力学,可以证明摆的运动可以用无量纲的非线性方程
[math]\displaystyle{ \frac{d^2 \theta}{d t^2} + \sin(\theta) = 0 }[/math]
where gravity points "downwards" and [math]\displaystyle{ \theta }[/math] is the angle the pendulum forms with its rest position, as shown in the figure at right. One approach to "solving" this equation is to use [math]\displaystyle{ d\theta/dt }[/math] as an integrating factor, which would eventually yield
where gravity points "downwards" and [math]\displaystyle{ \theta }[/math] is the angle the pendulum forms with its rest position, as shown in the figure at right. One approach to "solving" this equation is to use [math]\displaystyle{ d\theta/dt }[/math] as an integrating factor, which would eventually yield
描述,其中重力指向“下方”,[math]\displaystyle{ \theta }[/math] 是摆与其静止位置形成的角度,如右图所示。“解”这个方程的方法之一是用 [math]\displaystyle{ d\theta/dt }[/math] 作为积分因子,最终得
[math]\displaystyle{ \int{\frac{d \theta}{\sqrt{C_0 + 2 \cos(\theta)}}} = t + C_1 }[/math]
which is an implicit solution involving an elliptic integral. This "solution" generally does not have many uses because most of the nature of the solution is hidden in the nonelementary integral (nonelementary unless [math]\displaystyle{ C_0 = 2 }[/math]).
which is an implicit solution involving an elliptic integral. This "solution" generally does not have many uses because most of the nature of the solution is hidden in the nonelementary integral (nonelementary unless [math]\displaystyle{ C_0 = 2 }[/math]).
这是一个含椭圆积分的隐式解。这个“解”通常没什么用,因为这个解的大部分性质都隐藏在非初等函数积分中(除非[math]\displaystyle{ C_0 = 2 }[/math],否则是非初等的)。
Another way to approach the problem is to linearize any nonlinearities (the sine function term in this case) at the various points of interest through Taylor expansions. For example, the linearization at [math]\displaystyle{ \theta = 0 }[/math], called the small angle approximation, is
Another way to approach the problem is to linearize any nonlinearities (the sine function term in this case) at the various points of interest through Taylor expansions. For example, the linearization at [math]\displaystyle{ \theta = 0 }[/math], called the small angle approximation, is
另一种解决这个问题的方法是利用泰勒展开将任意非线性项(此时为正弦函数项)在某些感兴趣的点线性化。例如,在[math]\displaystyle{ \theta = 0 }[/math] 的点附近线性化(称为小角度近似)为
[math]\displaystyle{ \frac{d^2 \theta}{d t^2} + \theta = 0 }[/math]
since [math]\displaystyle{ \sin(\theta) \approx \theta }[/math] for [math]\displaystyle{ \theta \approx 0 }[/math]. This is a simple harmonic oscillator corresponding to oscillations of the pendulum near the bottom of its path. Another linearization would be at [math]\displaystyle{ \theta = \pi }[/math], corresponding to the pendulum being straight up:
since [math]\displaystyle{ \sin(\theta) \approx \theta }[/math] for [math]\displaystyle{ \theta \approx 0 }[/math]. This is a simple harmonic oscillator corresponding to oscillations of the pendulum near the bottom of its path. Another linearization would be at [math]\displaystyle{ \theta = \pi }[/math], corresponding to the pendulum being straight up:
因为 [math]\displaystyle{ \theta \approx 0 }[/math] 时,有 [math]\displaystyle{ \sin(\theta) \approx \theta }[/math]。这是一个简谐振子,对应于摆在其路径底部附近的摆动。另一种线性化方法是在 [math]\displaystyle{ \theta = \pi }[/math]附近线性化,对应于运动到最高点的摆:
[math]\displaystyle{ \frac{d^2 \theta}{d t^2} + \pi - \theta = 0 }[/math]
since [math]\displaystyle{ \sin(\theta) \approx \pi - \theta }[/math] for [math]\displaystyle{ \theta \approx \pi }[/math]. The solution to this problem involves hyperbolic sinusoids, and note that unlike the small angle approximation, this approximation is unstable, meaning that [math]\displaystyle{ |\theta| }[/math] will usually grow without limit, though bounded solutions are possible. This corresponds to the difficulty of balancing a pendulum upright, it is literally an unstable state.
since [math]\displaystyle{ \sin(\theta) \approx \pi - \theta }[/math] for [math]\displaystyle{ \theta \approx \pi }[/math]. The solution to this problem involves hyperbolic sinusoids, and note that unlike the small angle approximation, this approximation is unstable, meaning that [math]\displaystyle{ |\theta| }[/math] will usually grow without limit, though bounded solutions are possible. This corresponds to the difficulty of balancing a pendulum upright, it is literally an unstable state.
因为 [math]\displaystyle{ \theta \approx \pi }[/math] 时,有 [math]\displaystyle{ \sin(\theta) \approx \pi - \theta }[/math]。这个问题的解含双曲正弦曲线;注意到不同于小角度近似,它是不稳定的,这意味着 [math]\displaystyle{ |\theta| }[/math] 通常会无限增长,尽管有界解是可能的。这相当于平衡一个直立的钟摆的难度,它实际上是一种不稳定的状态。
One more interesting linearization is possible around [math]\displaystyle{ \theta = \pi/2 }[/math], around which [math]\displaystyle{ \sin(\theta) \approx 1 }[/math]:
One more interesting linearization is possible around [math]\displaystyle{ \theta = \pi/2 }[/math], around which [math]\displaystyle{ \sin(\theta) \approx 1 }[/math]:
一个更有趣的线性化可能围绕着 math theta pi / 2 / math,围绕着 math sin ( theta) approx1 / math:
- [math]\displaystyle{ \frac{d^2 \theta}{d t^2} + 1 = 0. }[/math]
[math]\displaystyle{ \frac{d^2 \theta}{d t^2} + 1 = 0. }[/math]
Math frac ^ 2 theta } d t ^ 2} + 10. / math
This corresponds to a free fall problem. A very useful qualitative picture of the pendulum's dynamics may be obtained by piecing together such linearizations, as seen in the figure at right. Other techniques may be used to find (exact) phase portraits and approximate periods.
This corresponds to a free fall problem. A very useful qualitative picture of the pendulum's dynamics may be obtained by piecing together such linearizations, as seen in the figure at right. Other techniques may be used to find (exact) phase portraits and approximate periods.
这相当于一个自由落体问题。一个非常有用的定性图片的钟摆的动态可以得到一起拼凑这样的线性化,如图中所示。其他技术可用于寻找(精确的)相位图和近似周期。
Types of nonlinear dynamic behaviors
Types of nonlinear dynamic behaviors
非线性动力学行为的类型
- Amplitude death – any oscillations present in the system cease due to some kind of interaction with other system or feedback by the same system
- Chaos – values of a system cannot be predicted indefinitely far into the future, and fluctuations are aperiodic
- Multistability – the presence of two or more stable states
- Solitons – self-reinforcing solitary waves
- Limit cycles – asymptotic periodic orbits to which destabilized fixed points are attracted.
- Self-oscillations - feedback oscillations taking place in open dissipative physical systems.
Examples of nonlinear equations
Examples of nonlinear equations
非线性方程的例子
- Ball and beam system
- Bellman equation for optimal policy
- Richards equation for unsaturated water flow
See also
See also
参见
References
References
参考资料
- ↑ "Explained: Linear and nonlinear systems". MIT News. Retrieved 2018-06-30.
- ↑ "Nonlinear systems, Applied Mathematics - University of Birmingham". www.birmingham.ac.uk (in British English). Retrieved 2018-06-30.
- ↑ "Nonlinear Biology", The Nonlinear Universe, The Frontiers Collection (in English), Springer Berlin Heidelberg, 2007, pp. 181–276, doi:10.1007/978-3-540-34153-6_7, ISBN 9783540341529
- ↑ Korenberg, Michael J.; Hunter, Ian W. (March 1996). "The identification of nonlinear biological systems: Volterra kernel approaches". Annals of Biomedical Engineering (in English). 24 (2): 250–268. doi:10.1007/bf02667354. ISSN 0090-6964.
- ↑ Mosconi, Francesco; Julou, Thomas; Desprat, Nicolas; Sinha, Deepak Kumar; Allemand, Jean-François; Vincent Croquette; Bensimon, David (2008). "Some nonlinear challenges in biology". Nonlinearity (in English). 21 (8): T131. Bibcode:2008Nonli..21..131M. doi:10.1088/0951-7715/21/8/T03. ISSN 0951-7715.
- ↑ Gintautas, V. (2008). "Resonant forcing of nonlinear systems of differential equations". Chaos. 18 (3): 033118. arXiv:0803.2252. Bibcode:2008Chaos..18c3118G. doi:10.1063/1.2964200. PMID 19045456.
- ↑ Stephenson, C.; et., al. (2017). "Topological properties of a self-assembled electrical network via ab initio calculation". Sci. Rep. 7: 41621. Bibcode:2017NatSR...741621S. doi:10.1038/srep41621. PMC 5290745. PMID 28155863.
- ↑ de Canete, Javier, Cipriano Galindo, and Inmaculada Garcia-Moral (2011). System Engineering and Automation: An Interactive Educational Approach. Berlin: Springer. p. 46. ISBN 978-3642202292. https://books.google.com/?id=h8rCQYXGGY8C&pg=PA46&lpg=PA46&dq=most+systems+are+inherently+nonlinear+in+nature#v=onepage&q=most%20systems%20are%20inherently%20nonlinear%20in%20nature&f=false. Retrieved 20 January 2018.
- ↑ Nonlinear Dynamics I: Chaos -{zh-cn:互联网档案馆; zh-tw:網際網路檔案館; zh-hk:互聯網檔案館;}-的存檔,存档日期2008-02-12. at MIT's OpenCourseWare
- ↑ Lazard, D. (2009). "Thirty years of Polynomial System Solving, and now?". Journal of Symbolic Computation. 44 (3): 222–231. doi:10.1016/j.jsc.2008.03.004.
- ↑ Billings S.A. "Nonlinear System Identification: NARMAX Methods in the Time, Frequency, and Spatio-Temporal Domains". Wiley, 2013
- ↑ David Tong: Lectures on Classical Dynamics
Further reading
Further reading
进一步阅读
- Diederich Hinrichsen and Anthony J. Pritchard
作者 Diederich Hinrichsen 和 Anthony j. Pritchard (2005
2005年). Mathematical Systems Theory I - Modelling, State Space Analysis, Stability and Robustness
数学系统理论 i-建模,状态空间分析,稳定性和鲁棒性. Springer Verlag
出版商 Springer Verlag. ISBN [[Special:BookSources/9783540441250
9783540441250|9783540441250
9783540441250]].
}}
}}
- Jordan
最后一个乔丹, D. W.
首先是 D.w。; Smith
最后2个史密斯, P. (2007
2007年). Nonlinear Ordinary Differential Equations
非线性常微分方程 (fourth
第四版 ed.). Oxford University Press
牛津大学出版社. ISBN [[Special:BookSources/978-0-19-920824-1
[国际标准图书编号978-0-19-920824-1]|978-0-19-920824-1
[国际标准图书编号978-0-19-920824-1]]].
}}
}}
- Khalil
最后的哈利勒, Hassan K.
首先是哈桑 · k。 (2001
2001年). Nonlinear Systems
非线性系统. Prentice Hall
出版商 Prentice Hall. ISBN [[Special:BookSources/978-0-13-067389-3
[国际标准图书编号978-0-13-067389-3]|978-0-13-067389-3
[国际标准图书编号978-0-13-067389-3]]].
}}
}}
- [[Erwin Kreyszig
作者 / 链接 Erwin Kreyszig |Kreyszig, Erwin
首先是欧文]] (1998
1998年). [https://archive.org/details/advancedengineer0008krey
Https://archive.org/details/advancedengineer0008krey Advanced Engineering Mathematics
高等工程数学]. Wiley
出版商 Wiley. ISBN [[Special:BookSources/978-0-471-15496-9
[国际标准图书编号978-0-471-15496-9]|978-0-471-15496-9
[国际标准图书编号978-0-471-15496-9]]]. https://archive.org/details/advancedengineer0008krey
Https://archive.org/details/advancedengineer0008krey.
}}
}}
- [[Eduardo D. Sontag
作者: Eduardo d. Sontag |Sontag
最后一个桑塔格, Eduardo
首先是爱德华多]] (1998
1998年). Mathematical Control Theory: Deterministic Finite Dimensional Systems. Second Edition
数学控制理论: 确定性有限维系统。第二版. Springer
出版商斯普林格. ISBN [[Special:BookSources/978-0-387-98489-6
[国际标准图书编号978-0-387-98489-6]|978-0-387-98489-6
[国际标准图书编号978-0-387-98489-6]]].
}}
}}
External links
External links
外部链接
- Nonlinear Model Library模板:Snd (in MATLAB) a Database of Physical Systems
模板:Differential equations topics
Category:Dynamical systems
类别: 动力系统
Category:Concepts in physics
分类: 物理概念
This page was moved from wikipedia:en:Nonlinear system. Its edit history can be viewed at 非线性系统/edithistory
- CS1 British English-language sources (en)
- CS1 English-language sources (en)
- Webarchive模板wayback链接
- 调用重复模板参数的页面
- Articles with hatnote templates targeting a nonexistent page
- Missing redirects
- 含有受损文件链接的页面
- 保护状态与保护标志不符的页面
- AC with 0 elements
- Pages with red-linked authority control categories
- Nonlinear systems
- Dynamical systems
- Concepts in physics
- 待整理页面