M.C.埃舍尔的数学艺术欣赏
- 作者:佚名
- 转自:member.21maths.com/
无论这个问题从属于数学领域还是从属于艺术领域,它对于我仍然是一个未解的问题。

———— M.C.埃舍尔
介绍
埃舍尔把自己称为一个“图形艺术家”,他专门从事于木版画和平版画。1898年他出生在荷兰的Leeuwarden,全名叫Maurits Cornelis Escher。他的家庭设想他将来能跟随他的父亲从事建筑事业,但是他在学校里那可怜的成绩以及对于绘画和设计的偏爱最终使得他从事图形艺术的职业。他的工作成果直到五十年代才被注意,1956年他举办了他的第一次重要的画展,这个画展得到了《时代》杂志的好评,并且获得了世界范围的名望。在他的最热情的赞美者之中不乏许多数学家,他们认为在他的作品中数学的原则和思想得到了非同寻常的形象化。因为这个荷兰的艺术家没有受过中学以外的正式的数学训练,因而这一点尤其令人赞叹。随着他的创作的发展,他从他读到的数学的思想中获得了巨大灵感,他工作中经常直接用平面几何和射影几何的结构,这使他的作品深刻地反映了非欧几里德几何学的精髓,下面我们将看到这一点。他也被悖论和“不可能”的图形结构所迷住,并且使用了罗杰•彭罗斯的一个想法发展了许多吸引人的艺术成果。这样,对于学数学的学生,埃舍尔的工作围绕了两个广阔的区域:“空间几何学”和我们或许可以叫做的“空间逻辑学”。
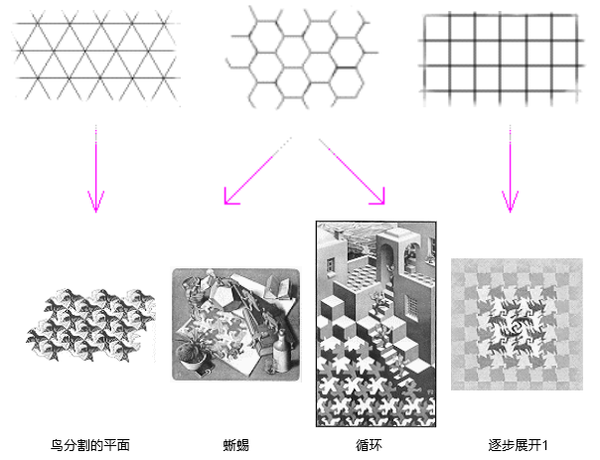
镶嵌图形
规则的平面分割叫做镶嵌,镶嵌图形是完全没有重叠并且没有空隙的封闭图形的排列。一般来说,构成一个镶嵌图形的基本单元是多边形或类似的常规形状,例如经常在地板上使用的方瓦。然而,埃舍尔被每种镶嵌图形迷住了,不论是常规的还是不规则的;并且对一种他称为metamorphoses(变形)的形状特别感兴趣,这其中的图形相互变化影响,并且有时突破平面的自由。他的兴趣是从1936年开始的,那年他旅行到了西班牙并且在Alhambra看到了当地使用的瓦的图案。他花了好几天勾画这些瓦面,过后宣称这些“是我所遇到的最丰富的灵感资源”,1957年他写了一篇关于镶嵌图形的文章,其中评论道:“在数学领域,规则的平面分割已从理论上研究过了……难道这意味着它只是一个严格的数学的问题吗?按照我的意见,它不是。数学家们打开了通向一个广阔领域的大门,但是他们自己却从未进入该领域。从他们的天性来看他们更感兴趣的是打开这扇门的方式,而不是门后面的花园。”
无论这对数学家是否公平,有一点是真实的——他们指出了在所有的常规的多边形中,仅仅三角形,正方形,和正六边形能被用于镶嵌。但许多其他不规则多边形平铺后也能形成镶嵌,例如有许多镶嵌就使用了不规则的五角星形状。埃舍尔在他的镶嵌图形中利用了这些基本的图案,他用几何学中的反射、平滑反射、变换和旋转来获得更多的变化图案。他也精心地使这些基本图案扭曲变形为动物、鸟和其他的形状。这些改变不得不通过三次、四次甚至六次的对称以便得到镶嵌图形。这样做的效果既是惊人的,又是美丽的。
在“蜥蜴”里,镶嵌而成的蜥蜴嬉笑地逃离二维平面的束缚到桌面放风,然后又重新陷入原来的图案。埃舍尔在许多六边形的镶嵌图形中使用了这个图案模式。在“逐步展开1”中,可以追溯到这个方形的镶嵌图形从边缘到中间的不断扭曲转化。
多面体
规则的几何体,例如多面体,对埃舍尔而言具有特殊的魅力。他把它们作为许多作品的主题,并且在许多作品中作为第二重要的元素出现。仅仅只有五种多面体被称为理想的多面体。四面体有四个三角形的表面;正方体有六个正方形的表面;八面体有八个三角形的表面;十二面体有十二个五边形的表面;而二十面体有二十个三角形的表面。在木版画“四个常规的几何体”中,埃舍尔把理想多面体中的四个匀称地交叉了,并且使它们呈半透明状以便每个都可以透过其它得以辨认,请看漏了哪个?
有许多有趣的几何体可以通过理想几何体的交叉和星形化来获得,即几何体的每一面都由表面为三角形的金字塔形来替代,通过这种变换,多面体转变成了一个尖锐的,三维的星形几何体。在埃舍尔的作品“有序和无序”中我们可以发现.一个美丽的星形十二面体,星形的轮廓隐现在一个水晶球中,严谨构造的美丽与在桌子上混乱摆放的其他的杂物形成了鲜明的对比。注意一下还可以猜测到光的来源,球面上反射出左上方有一个明亮的窗口。
交叉的几何体也常常出现在埃舍尔的作品中,其中最有趣的是一幅木版画“星”。这是一个由八面体、四面体、立方体和其他东西交叉构成的几何体,我们不妨这样认为,如果埃舍尔简单地画一些数学的形状并且把它们放在一起,我们也许永远不可能听说他或他的作品。相反,通过将变色龙放置在多面体内并向我们嘲笑和恐吓的构思,埃舍尔给了我们一种奇异的视觉刺激,使我们对他的画刮目相看。显然,数学家们对埃舍尔的作品颇为赞赏的另外的原因就是所有伟大的数学发现背后都具有与此相同的感性和创意。
空间的形状
在埃舍尔用数学观点完成的所有重要的作品中,最重要是处理空间性质的那些。他的木版画“三个方向交叉的平面”是评论这些作品的好例子,因为它显示了艺术家对空间维度的关心,以及用二维的方式表现三维的能力。在下一节我们将看到,埃舍尔经常利用了后者的特征来获得令人震惊的视觉效果。
受一位名叫H.S.MCoxeter的数学家在一本书中绘画的启发,埃舍尔创造了许多美丽的双曲线空间的作品,例如木版画“圆形限制III”。这是非欧几里德几何学的二种空间之一,在埃舍尔的作品中它的原型实际上源自法国数学家Poincaré。要得到这个空间的感觉,必须想象你实际上是在图像的内部。当你从它的中心走向图像的边缘,你会象图像里的鱼一样缩小,从而到达你移动后实际的位置,这似乎是无限度的,而实际上你仍然在这个双曲线空间的内部,你必须走无限的距离才能到达欧几里德空间的边缘,这一点确实不是显而易见的。然而,如果你能仔细观察的话,你还可以注意到一些其他的事情,例如所有类似的三角形都一样大小,以及你能画没有直边却有四个直角的图形,这就是说,这个空间没有任何正方形或矩形。这确实是一个奇怪的地方!
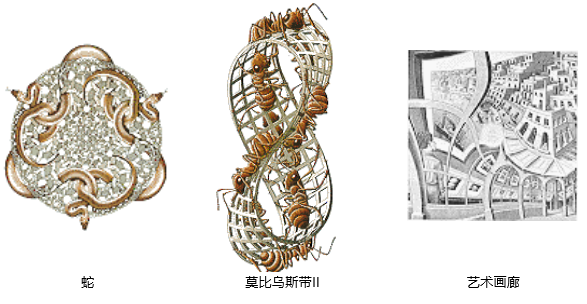
更不平常的是木版画“蛇”所表现的空间,在缠绕和缩小的环的表现下,空间既向边界也向中心延伸并且无穷无尽。如果你在这一空间里,你将是什么模样?除了欧几里德几何学和非欧几里德几何学,埃舍尔对拓扑学的视觉效果也很感兴趣,拓扑学是在他艺术创作的鼎盛期发展起来的一个数学分支。拓扑学关注空间那些扭曲后依然不变的性质,这种扭曲可以是拉长或弯曲,但不是撕裂或折断。拓扑学家们忙于向世界展示那些奇怪的物体,莫比乌斯带也许是最主要的例子,埃舍尔利用它创作了许多作品。它有一个令人感兴趣的性质————它只有一条边和一个面。这样,如果你在“莫比乌斯带II”上跟踪蚂蚁的路径,你将发现它们不是在相反的面上走,而是都走在一个面上。制作一个莫比乌斯带很容易;只要用剪刀把纸剪成条状,将它扭曲180度,然后用胶水或胶带粘住两头就可以了。如果你试图把这条东西纵向的剪成两半,请你预想一下会发生什么情况?
另外一幅很著名的平版画,叫做“艺术画廊”,它探索了空间逻辑与拓扑的性质。一个年轻人在一个艺术画廊正看着海边小镇的一角,在船坞边有一家小店,在店里面是一个艺术画廊及一个年轻人--他正朝着海边小镇的一角望去……但是等一下!发生了什么?埃舍尔的所有作品都值得细细观赏,但是这一次尤其特别。某种程度上,埃舍尔把空间由二维变成了三维,使人感觉到那个年轻人同时既在画像内又在画像外面。
达到这样效果的秘密在艺术家创作这幅平版画的格子草图中有所显现注意格子的边框连续地按顺时针方向排列这一规律,并且特别注意这个技巧的关键在中间的一个洞。一个数学家将这叫做奇异点,一个空间的结构不再保持完整的地方,要将整个空间编织成一个无洞的整体是非常困难的,埃舍尔也宁可保持这种现状,并且把他的商标initials放在了奇异点的中心。
空间的逻辑
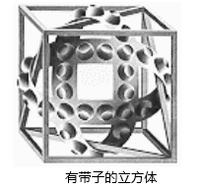
这里所说的空间的逻辑是指物理中的物体之间的那些空间的必要的关系,在产生违背视觉的悖论时,被叫做视错觉。所有的艺术家都关心空间的逻辑,而且许多艺术家深入地探索了它的规律,例如毕加索。埃舍尔知道:立体几何学决定了空间的逻辑,同样地,空间的逻辑也经常决定其自身的立体几何学。他经常使用的空间逻辑的特征之一是展示在凹面和凸面物体上的光和阴影。在平版画"有带子的立方体"中,带子上的凹凸是我们觉察它们怎样与立方体缠绕在一起的视觉线索。然而,如果我们相信我们的眼睛,那么我们不能相信这带子!
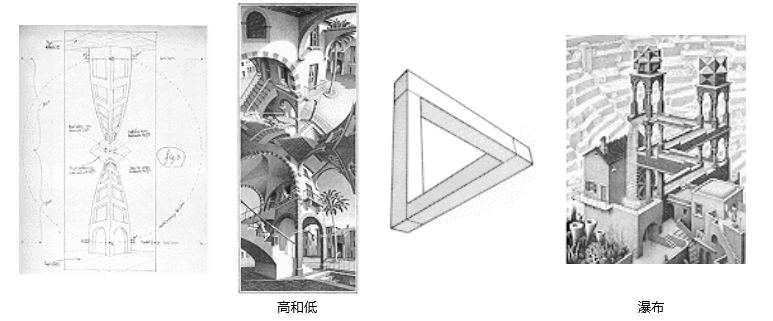
埃舍尔关心的另一个主要方面是透视。在任何透视画中,趋向消失的点被选择用来代表无穷远。正是由于Alberti、Desargues以及其他一些人在文艺复兴时期对透视和趋向无限的点的研究直接导致了现代射影几何学的出现。通过一些不平常地消失的点的引导并迫使一幅作品的基本元素去服从于它们,埃舍尔能够使作品"上和下"、"高和低"表现的场景取决于观众观察它的目光如何。在他的名为"高和低"的透视作品中,艺术家总共设置了五个消失点:上方的左边和右边,底部的左方和右边,以及中心。其结果是:在作品的下半部观众是在往上看,但是在作品的上半部,观众是在朝下看。为了强调他所取得的成功,埃舍尔把上半部和下半部合成了一幅完整的作品。
这种另类的“不可能的绘画”用二维的图形表示并构造一个三维的物体,它们主要依靠人的大脑通过视觉暗示来理解,埃舍尔创作了许多这种表现反常规图形的作品。其中最吸引人的一个创意源于一个叫罗杰•彭罗斯的数学家所提出的不可能的三角形。在这幅名叫“瀑布”的平版画中,两个彭罗斯三角形被结合成一个不可能的形状。一个人如果明白空间的逻辑对如此的一个构造就必然会觉得不可思议:瀑布是一个封闭系统,但它却能使作坊车轮象一台永动机一样连续地转动,这就违背了能量守衡的定律。(请注意一下在塔上交叉的立方体和八面体。)
自我复制和信息科学
我们对埃舍尔的艺术所作的最后研究包括了其艺术与信息科学、人工智能的关系,这在先前的研究中被忽略了,但是这一点的重要性被道格拉斯•R•霍夫施塔特细心的发现了,并写在他赢得1980普利策奖的《Gödel,Escher,Bach:一条永恒的金带》一书中。埃舍尔表现的一个核心概念是自我复制--这被许多人认为已经逼近了大脑知觉这个难题的核心,并且至今计算机还不具备成功地模仿人类大脑处理信息能力。平版画“互绘的双手”和木版画“鱼和规模”用不同的方法表现了这个思想。前者的自我复制是直接的,概念化的。双手互绘对方,互绘的方式就是意识思考和构建自己的方式,神奇的是,在这里自我和自我复制是连结在一起的,也是相互同等的。
另一方面,在“鱼和规模”这幅画中,自我复制具有更大的功能;人们也许宁愿称之为自我相似。这样木板画描述的就不仅是鱼,而是所有的有机体。因为,尽管从物理角度来说,我们不是由微小的自我复制建造起来的,但是,从信息理论角度说,我们的确是以这样一种方式建立起来的,因为我们身体上的每一个细胞都以DNA的形式携带了我们个体的完整信息。在更深层次的水平上,自我复制是一种我们的认知世界互相反映和互相交错的结果。我们每一个人都像一本书里的正在读他(或她)自己的故事的人物,或者像反映它自身风景的一面镜子那样。许多埃舍尔的作品都展现了相互交错的世界这个主题,我们在这里只举一个这样例子。正如通常埃舍尔对这个想法的处理那样,平版画“三个圆球II”利用了球形镜面的反射原理。这里,正如Hofstatder提到的那样“世界的每个部分似乎都包含它,也似乎都被包含进去了……”。这些球体彼此相互反射,折射出艺术家自己、他工作的房间和他用来画这些圆球的纸。
最后,就象本文开头一样我们用这幅埃舍尔的自我肖像结束本文,它表现了艺术家的工作,艺术家被反映在他的作品中。
结论
我们这里仅仅分析了埃舍尔在1972年去世之前留给我们的几百幅素描、平版画和木版画中的一小部分。关于他的作品的深度、意义和重要性还有很多可谈,或已被谈过。读者可以进一步更深入地去探索M.C.埃舍尔留下的丰富的遗产,并且再思考他从幻想的世界、数学的世界和我们现实的世界中抽象出的这些世界之间丰富的联系。