三体问题

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
跳到导航 跳到搜索
位于不等边三角形顶点且初始速度为零的三个相同物体的近似轨迹。可以看出，在质量中心，根据动量守恒定律，保持不变。

在物理学和经典力学领域中，三体问题 Three-body problem是根据牛顿运动定律和牛顿万有引力定律按照三点处质量体的初始位置和速度（或动量）求出它们随后的运动的问题。[1] 三体是N体问题中的一个特例。与双体问题不同的是，三体问题不存在一般的闭式解，[1]因为产生的动力系统对于大多数初始条件来说是混沌的，所以一般需要数值方法求解。


历史上看，第一个被拓展研究的特定三体问题是月球、地球和太阳构成的“三体”问题。[2]从现代意义上讲，拓展的三体问题可以是经典力学或量子力学中模拟三个粒子运动的任何问题。

数学描述

三体的数学表达式可以用三个质量为[math]\displaystyle{ m_i }[/math]的相互作用的物体的矢量位置[math]\displaystyle{ \mathbf{r_i} = (x_i, y_i, z_i) }[/math]的牛顿运动方程来表示：

[math]\displaystyle{ \begin{align} \ddot{\mathbf{r}_{\mathbf{1}}} &= -G m_2 \frac{\mathbf{r_1} - \mathbf{r_2}}{|\mathbf{r_1} - \mathbf{r_2}|^3} - G m_3 \frac{\mathbf{r_1} - \mathbf{r_3}}{|\mathbf{r_1} - \mathbf{r_3}|^3}, \\ \ddot{\mathbf{r}_{\mathbf{2}}} &= -G m_3 \frac{\mathbf{r_2} - \mathbf{r_3}}{|\mathbf{r_2} - \mathbf{r_3}|^3} - G m_1 \frac{\mathbf{r_2} - \mathbf{r_1}}{|\mathbf{r_2} - \mathbf{r_1}|^3}, \\ \ddot{\mathbf{r}_{\mathbf{3}}} &= -G m_1 \frac{\mathbf{r_3} - \mathbf{r_1}}{|\mathbf{r_3} - \mathbf{r_1}|^3} - G m_2 \frac{\mathbf{r_3} - \mathbf{r_2}}{|\mathbf{r_3} - \mathbf{r_2}|^3}. \end{align} }[/math]


其中[math]\displaystyle{ G }[/math]为万有引力常数。[3][4]这是一组9个二阶微分方程构成的方程组。这个问题也可以用哈密顿形式等价表示，此时可以用一组18个一阶微分方程来描述，这些方程分别对应于位置[math]\displaystyle{ \mathbf{r_i} }[/math]和动量[math]\displaystyle{ \mathbf{p_i} }[/math]的一个分量：

[math]\displaystyle{ \frac{d \mathbf{r_i}}{dt} = \frac{\partial \mathcal{H}}{\partial \mathbf{p_i}}, \qquad \frac{d\mathbf{p_i}}{dt} = -\frac{\partial \mathcal{H}}{\partial \mathbf{r_i}}, }[/math]


其中[math]\displaystyle{ \mathcal{H} }[/math]是哈密顿 Hamiltonian函数：

[math]\displaystyle{ \mathcal{H} = -\frac{G m_1 m_2}{|\mathbf{r_1} - \mathbf{r_2}|}-\frac{G m_2 m_3}{|\mathbf{r_3} - \mathbf{r_2}|} -\frac{G m_3 m_1}{|\mathbf{r_3} - \mathbf{r_1}|} + \frac{\mathbf{p_1}^2}{2m_1} + \frac{\mathbf{p_2}^2}{2m_2} + \frac{\mathbf{p_3}^2}{2m_3}. }[/math]


这种情况下，[math]\displaystyle{ \mathcal{H} }[/math]仅仅是系统的总能量，重力加上动能。


限制性三体问题

圆形受限三体问题是在太阳系中发现的椭圆轨道的有效近似，这可以看作是由于两个主要天体的重力以及它们旋转（科里奥利）产生的离心效应而产生的势的组合效果是动态的，未显示）。然后可以将拉格朗日点视为合成表面上梯度为零的五个位置（显示为蓝线），表明力在那里处于平衡状态。


限制性三体问题有庞加莱引入，作为三体问题的一个简化的版本。 在限制性三体问题中，[3]一个质量可忽略不计的天体(“小行星”)在两个质量巨大的天体的影响下运动。由于质量可忽略不计，小行星对这两个质量巨大的天体所施加的力可忽略不计，因此可以可以用两个物体的运动来描述，对该系统进行分析。通常这种两体运动被认为是由围绕质心的圆形轨道组成的，并且假定小行星在圆形轨道所定义的平面内运动。

受限制的三体问题比完全的三体问题更容易从理论上分析。它也具有实际意义，因为它准确地描述了许多现实世界的问题，其中最重要的例子是地球-月亮-太阳的系统，这也是在三体问题的历史发展中有重要地位的一个典型。


在数学的表述上，设[math]\displaystyle{ m_{1,2} }[/math]为两个大质量天体的质量，二维平面坐标[math]\displaystyle{ (x_1, y_1) }[/math]和[math]\displaystyle{ (x_2, y_2) }[/math]分别为小行星的坐标。简单起见，选择的单位应该要确保两大质量天体的距离和重力常数都等于1。则小行星的运动可以用公式描述为：

[math]\displaystyle{ \begin{align} \frac{d^2 x}{dt^2} = -m_1 \frac{x - x_1}{r_1^3} - m_2 \frac{x - x_2}{r_2^3} \\ \frac{d^2 y}{dt^2} = -m_1 \frac{y - y_1}{r_1^3} - m_2 \frac{y - y_2}{r_2^3}, \end{align} }[/math]


其中[math]\displaystyle{ r_i = \sqrt{(x - x_i)^2 + (y - y_i)^2} }[/math]，在这种形式下，运动方程通过坐标具有明确的时间依赖性[math]\displaystyle{ x_i(t), y_i(t) }[/math]。但可以通过转换为旋转参考系来消除这种时间相关性，从而简化了后续的分析。

我们从运动方程上可以看出，限制性三体问题有两个自由度，即以两维的位置变量和相应的动量变量就可以完全刻画其运动。若要完全求解限制性三体问题，我们需要在总能量之外，找到第二个守恒量，庞加莱发现这第二个守恒量是不存在，即证明了限制性三体问题的不可解性。


在庞加莱接近临终的时候，通过对限制性三体问题的研究，他提出庞加莱最后几何定理，由美国数学家Birkhoff证明。定理内容为：考虑环面[math]\displaystyle{ [0,1]\times \mathbb R/\mathbb Z }[/math]上的一个保面积的微分同胚，假设它保持两个边界，并把两个边界朝想法的方向扭转，则它有两个不动点。这个定理意味着限制性三体问题中周期轨的存在性。 这个定理有深刻的拓扑内涵，对后世数学产生了巨大的影响。一个重要的结果就是导致了Arnold猜想和辛几何这一领域的诞生。

Hill月球问题

三体问题的级数解

由简单的代数表达式和积分给出的三体没有一般的解析解。[1] 此外，除特殊情况，三个物体的运动一般是不重复的。[5]


另一方面，1912年芬兰数学家Karl Fritiof Sundman 证明了三体问题存在一个 t1/3幂次方的级数解。[6]除了对应于角动量为零的初始条件外，这个级数对所有实数t都收敛。


证明这个结果的一个重要问题是，该序列的收敛半径是由到最近奇点的距离决定的。因此，有必要研究三体问题的可能奇点。三体问题中唯一的奇点是二元碰撞(两个粒子在瞬间的碰撞)和三元碰撞(三个粒子在瞬间的碰撞)，下面会进行简单的讨论。


无论是二元的还是三元的(事实上是任何数目) 碰撞都不太可能发生，因为已经证明它们对应于测度为零的一组初始条件。然而，没有已知的标准被放在初始状态，以对相应的解避免碰撞。因此，**Sundman**的求解方法包括以下步骤:

1. 使用适当的变量变化来继续分析二元碰撞之外的解，这个过程称为正则化。

2. 证明只有在角动量L消失时才会发生三元碰撞。通过将初始数据限制为L ≠ 0，从三体问题的变换方程中删除了所有实数奇点。

3. 证明了如果L≠0，则不仅不存在三元碰撞，而且系统严格有界远离三元碰撞。这意味着，通过对微分方程使用柯西存在性定理，在以实际轴为中心的复平面（Kovalevskaya的阴影）中，一个条带区域（取决于L的值）中不存在复奇点。

4. 找到一个保角变换，把这个条带映射到单位圆盘。例如，如果s=t1/3（正则化后的新变量），并且[math]\displaystyle{ \left | ln s \right |\leq \beta }[/math]（需要证明），则映射可由下式给出：

[math]\displaystyle{ \sigma = \frac{e^\frac{\pi s}{2\beta} - 1}{e^\frac{\pi s}{2\beta} + 1}. }[/math]


上述即为完整的Sundman定律的证明。


但不幸运的是，对应的级数收敛得非常慢。也就是说，为了获得一定精度的值需要很多级数项，这样的解法并没有什么实际用途。的确，在1930年，大卫·贝洛里奇 David Beloriszky计算出，如果将Sundman级数用于天文观测，则计算将至少涉及108000000项。[7]

三体问题的最终运动

考虑任给初值得到的三体问题微分方程的解，假设这个解不带来碰撞，Chazy给出了所有可能的最终运动，即[math]\displaystyle{t\to \infty}[/math]时解的分类。


Chazy的结果可以描述如下。 我们考虑各种逻辑上的可能性包括：

1. B, 有界运动，即三个天体都在有界区域运动。

2. HE， 双曲椭圆型，即两个天体近似做椭圆运动，而另外一个天体渐进双曲运动，即渐进匀速直线。

3. PE, 抛物椭圆型，即两个天体做近似椭圆运动，另外一个天体渐进抛物运动，即位置趋向无穷远，速度趋向0。

4. H, 双曲型，即三个天体都趋向无穷远，速度趋向非零常数。

5. P，抛物型，即三个天体都趋向无穷远，速度趋向0。

6. HP, 抛物双曲型，即三个天体都趋向无穷远，速度有的趋向0，有的趋向常数。

7. OS, 振荡型(Oscillatory)，即存在一个时间子列，系统的直径趋向无穷，而沿另一个时间子列，系统直径有界。


前面六类多是两体问题的推广，而最后一类是三体问题的一类混沌解。在上文的限制性三体问题里会出现这种解，另外一个重要的模型出现这种解的是Sitnikov模型。考虑x-y平面上两个等质量天体做椭圆或者圆周运动，z轴上另外一个0质量的粒子在另外两个天体的吸引下运动。在这个模型中会出现OS型的解。

对三体问题所有可能的解的分类，除去上述的7类最终运动之外，还有可能是碰撞解。 如果系统发生碰撞，我们可以考虑对碰撞解做爆破，就是把空间放大时间变慢，这样从碰撞解中，我们可以得到自相似解。三体问题的自相似解主要是由下文的Euler共线解和Lagrange的等边三角形解刻画。 由此，我们对于三体问题所有可能的解的情况有一个分类。

特殊的求解方法

1767年， 莱昂哈德·欧拉 Leonhard Euler提出了三个周期解系列，其中三个质量在每个瞬间共线。


1772年，拉格朗日 Lagrange找到了一系列解，其中三个质量在每个瞬间形成一个等边三角形。这些解决方案与欧拉的共线解一起构成了三体问题的中心配置。这些解决方案对于任何质量比均有效，并且质量沿开普勒椭圆形运动。这四个族是唯一有明确解析公式的已知解决方案。在圆形受限三体问题的特殊情况下，这些解决方案在与原边一起旋转的框架中观察时，变为称为L1, L2, L3, L4和L5，并且叫做拉格朗日点，其中L3, L4是拉格朗日的对称解的实例。


在1892年至1899年的工作中，亨利·庞加莱 Henri Poincaré建立了无穷有限三体问题的周期解，以及将这些解法继续推广到一般三体问题的技巧。


1893年，迈塞尔提出了现在所说的毕达哥拉斯三体问题：将比例为3：4：5的三个质量置于3：4：5直角三角形的顶点处。布鲁 Burrau[8]在1913年进一步研究了这个问题。1967年，维克多·塞贝赫利 Victor Szebehely和 C、 弗雷德里克·彼得斯 C. Frederick Peters利用数值积分理论建立了这个问题的最终逃逸模型，同时找到了附近的周期解。[9]


20世纪70年代，米歇尔·赫农 Michel Hénon和 罗杰A.布鲁克 Roger A. Broucke各自找到了一套解决方案，这些解决方案构成了同一系列解决方案的一部分: 布鲁克-赫农-哈德吉德梅特里奥 Broucke–Henon–Hadjidemetriou族。在这个家族中，这三个物体都具有相同的质量，可以表现出逆行和直行两种形式。在布鲁克的一些解中，两个物体遵循同样的路径。[10]

三体问题的图 8 解在单个周期 T ≃ 6.3259 上的动画。[11]

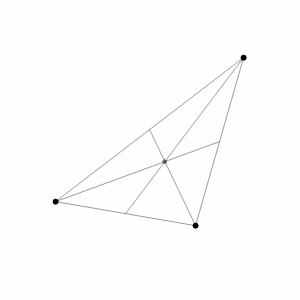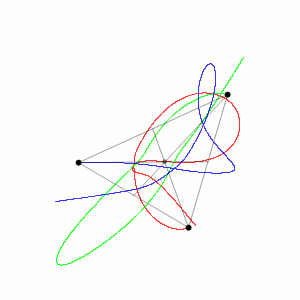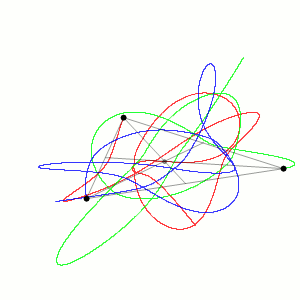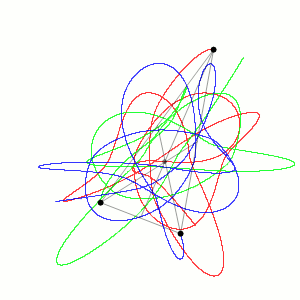
1993年，圣塔菲研究所的物理学家克里斯摩尔 Cris Moore提出了一种零角动量解，该解适用于三个相等质量围绕一个八字形运动。[12]这种方法在2000年由数学家阿兰·尚西奈 Alain Chenciner和理查德·蒙哥马利 Richard Montgomery证明。[13][14]在数值上证明了该解对于质量和轨道参数的小扰动是稳定的，这增加了在物理宇宙中可以观察到这种轨道的可能性。但有人认为不太可能发生这种情况，因为稳定​​性的范围小。在数值上证明了该解对于质量和轨道参数的小扰动是稳定的，这增加了在物理宇宙中可以观察到这种轨道的可能性。但是，由于稳定​​性的范围小，因此不太可能发生这种情况。例如，二元-二元散射事件导标号-8轨道的概率估计为1%的一小部分。[15]


2013年，贝尔格莱德物理研究所的物理学家 米洛万·乌瓦科夫 Milovan uvakov 和 维利科·德米特拉·伊诺维 Veljko dmitra inovi 发现了等质量零角动量三体问题的13种新的解族。[5][10]


2015年，物理学家 安娜·胡多马尔 Ana Hudomal 发现了14种等质量零角动量三体问题的新解族。


2017年，研究人员 李晓明 Xiaoming Li 和 廖世俊 Shijun Liao发现了669个等质量零角动量三体问题的新周期轨道。[16]2018年，不等质量的零动量系统又增加了1223个新解。[17]


2018年，李晓明和廖世俊提出了234个不等质量“自由落体”三体问题的解。[18]三体问题的自由落体公式从所有三个静止的物体开始。正因为如此，质量在一个自由落体配置不在一个闭合的“循环”轨道上运行，而是沿着一个开放的“轨道”向前和向后运行。


数值方法

尽管高精度需要大量的CPU时间，但是通过计算机可以使用数值积分可以得到问题的任意高精度解。在2019年，布林 Breen等人。提出了一种快速的神经网络求解器，使用数字积分器对其进行训练。[19]

历史

传统意义上的三个物体的引力问题可以追溯到1687年，当时 艾萨克·牛顿 Isaac Newton 发表了他的《自然哲学的数学原理》。在《原理》第一卷的第66号提案及其22个推论中，牛顿首次定义和研究了三个受相互扰动的重力吸引影响的巨大物体的运动问题。在第三册的第25至35条命题中，牛顿也迈出了第一步，将他的66号命题的结果应用到月球理论中，即月球在地球和太阳的引力影响下的运动。牛顿首先用微积分的技巧求解了两体问题，随后写下了三体问题的运动方程，并对它试图求解。但是他意识到三体问题求解的巨大困难，意识到天体之间的小扰动会使得轨道偏离标准的椭圆型轨道。但是他并不怀疑三体问题的可解性。他认为当天体偏离轨道的时候，上帝会出手把轨道推回到原来的状态。


Laplace和Lagrange引入了N体问题的平均法，并证明了太阳系大约在1000年左右的时间尺度之内的稳定性。

法国数学家庞加莱Poincare年轻的时候参加一个数学大奖赛，名字是奥斯卡国王二世奖。奥斯卡国王是当时挪威和瑞典的国王，非常热爱数学。庞加莱选择的题目是N体问题的级数解。在十九世纪，数学家普遍认为，对微分方程的求解即找到幂级数解。虽然庞加莱并没有解决这个问题，但是因为他的论文很精彩，仍然获得了这个奖。但是，他得奖之后以及论文发表之后，意识到论文有一个严重的错误。导致他购回了所有已经出版的论文，并纠正错误，写出一篇正确的论文，重新付印。庞加莱犯的这个错误是来自于其观念中认为三体问题是可解的，正如牛顿认为的那样。庞加莱后来正确的论文证明了在限制性三体问题中存在混沌，导致三体问题不能像两体问题那样求解。 这标志着混沌的发现。虽然庞加莱没有解决原来的级数解问题，但是他发现的混沌的意义远远大于原来的问题。原始的问题在三体情况下由Sundman解决，虽然得到的级数解收敛极其缓慢，没有实用价值。一般N体问题版本的原始问题由Qiudong Wang解决。

二十世纪中叶，Kolmogorov-Arnold-Moser通过对N体问题的研究提出了著名的KAM定理。这一定理意味着，N体问题中存在大量的不变环面，上面的轨道做拟周期运动。

亚美利哥·韦斯普奇 Amerigo Vespucci和随后的 伽利略·伽利雷 Galileo Galilei提出了三体问题; 1499年，韦斯普奇 Vespucci利用对月球位置的了解来确定自己在巴西的位置。因为这种方法适用于导航，特别是在海上确定经度，1720年代该方法变得非常技术实用。事实上确定经度的问题被 约翰·哈里森 John Harrison发明的航海经线仪所解决。但是，由于太阳和行星对月球绕地球运动的干扰作用，月球理论的准确性很低。


建立了长期竞争关系的 让·勒朗·达朗贝尔 Jean le Rond d'Alembert 和 亚历克西斯·克莱奥特 Alexis Clairaut都试图以某种普遍性来分析该问题。他们于1747年向皇家科学研究院提交了他们的第一批竞争分析。[20]在1740年代的巴黎，“三体问题”（法语：Problèmedes trois Corps）这个名字开始被普遍使用，与他们的研究有关。让·勒朗·达朗贝尔 Jean le Rond d'Alembert于1761年发布的文章表明该名称最早于1747年使用。[21]


2019年，Breen等人宣布了一种用于三体问题的快速神经网络求解器，使用数值积分器进行训练。[22]


其他涉及三体的问题

三体问题这个术语有时用在更一般的意义上来指涉及三个物体相互作用的任何物理问题。


氦原子是经典力学中引力三体问题的量子力学模拟，其中一个氦原子核和两个电子会产生反平方库仑相互作用。就像引力三体问题一样，氦原子的三体问题没有精确解。[23]


然而，在经典力学和量子力学中，除了平方反力外，还存在着一些非平凡相互作用规律，这些规律可以得到精确的解析解。有一种模型是由谐波吸引和排斥反立方体力的组合而成的。[24]该模型被认为是非平凡的，因为它与一组包含奇异性的非线性微分方程组相关联（例如，与单独的谐波相互作用相比，该关联能够得到易于求解的线性微分方程组）。在这两种情况下，三体问题类似于具有库仑相互作用的（无法解释的）模型，因此，有人提出将其作为直观理解诸如氦原子之类的物理系统的工具。[24][25]


引力三体问题也被通过广义相对论进行了研究。在物理上，相对论性的处理在引力场非常强的系统中变得非常必要，比如在黑洞的视界附近。然而，相对论性问题比牛顿力学困难得多，需要复杂的数值技术。即使是完整的两体问题（即任意质量比）在广义相对论中也没有严格的解析解。[26]

N体问题

三体问题是N体问题的一个特例，它描述了n个物体在其中一种物理力（如重力）下如何运动。这些问题具有收敛幂级数形式的全局解析解，比如，Karl F.Sundman证明n=3的情况，Qiudong Wang证明n>3的情况。然而，Sundman级数和Wang级数收敛速度太慢，无法用于实际目的；[27] 因此，目前有必要通过数值分析以数值积分的形式来近似解，或者在某些情况下，采用经典三角级数近似。原子系统，例如原子、离子和分子，可以用量子N体问题来处理。在经典物理系统中，N体问题通常是指一个星系或一个星系团；行星系统，如恒星、行星及其卫星，也可以被视为N体系统。一些应用可以方便地用扰动理论来处理，其中系统被认为是一个两体问题加上导致偏离假设的无扰动两体轨道的附加力。



三体小说

三体问题被中国作家刘慈欣用于科幻小说三部曲中的情节设计，也被用于作为第一卷和整个三部曲的书名。小说获得科幻界最高奖雨果奖。 小说假设在一个三体系统里面有一个文明，高度发达，开始对地球文明的征服。地球文明自救的方式是意识到黑暗森林的原理。在一个黑暗森林里，到处充满未知和风险，猎人需要隐藏好自己，一有风吹草动，猎人最好的办法就是朝吹动的地方开一枪。宇宙就如同一个黑暗森林，各个文明都隐藏其中。 因为知识的爆炸是指数式的，以千年的时间尺度，文明可以突飞猛进，而宇宙间的旅行所用的时间却远超这个时间尺度。 在这个情况下，发现一个文明，哪怕它再原始，也无法预测将来这个文明是不是对自己构成威胁，所以需要第一时刻消灭之。所以当三体人发现地球文明，并且要霸占地球的时候，地球人向三体人展示了其将三体文明的坐标暴露在整个宇宙中的能力，以此震慑三体人维系了一段时间的和平。其黑暗森林，降维打击等词已经成为中文中的成语。


参考文献

  1. ↑ 1.0 1.1 1.2 Barrow-Green, June (2008), "The Three-Body Problem", in Gowers, Timothy; Barrow-Green, June; Leader, Imre (eds.), The Princeton Companion to Mathematics, Princeton University Press, pp. 726–728
  2. ↑ "Historical Notes: Three-Body Problem". Retrieved 19 July 2017.
  3. ↑ 3.0 3.1 Barrow-Green, June (1997). Poincaré and the Three Body Problem. American Mathematical Society. pp. 8–12. Bibcode 1997ptbp.book.....B. ISBN 978-0-8218-0367-7. 
  4. ↑ "The Three-Body Problem" (PDF).
  5. ↑ 5.0 5.1 Cartwright, Jon (8 March 2013). "Physicists Discover a Whopping 13 New Solutions to Three-Body Problem". Science Now. Retrieved 2013-04-04.
  6. ↑ Barrow-Green, J. (2010). The dramatic episode of Sundman, Historia Mathematica 37, pp. 164–203.
  7. ↑ Beloriszky, D. (1930). "Application pratique des méthodes de M. Sundman à un cas particulier du problème des trois corps". Bulletin Astronomique. Série 2. 6: 417–434. Bibcode:1930BuAst...6..417B.
  8. ↑ Burrau (1913). "Numerische Berechnung eines Spezialfalles des Dreikörperproblems". Astronomische Nachrichten. 195 (6): 113–118. Bibcode:1913AN....195..113B. doi:10.1002/asna.19131950602.
  9. ↑ Victor Szebehely; C. Frederick Peters (1967). "Complete Solution of a General Problem of Three Bodies". Astronomical Journal. 72: 876. Bibcode:1967AJ.....72..876S. doi:10.1086/110355.
  10. ↑ 10.0 10.1 Šuvakov, M.; Dmitrašinović, V. "Three-body Gallery". Retrieved 12 August 2015.
  11. ↑ Here the gravitational constant G has been set to 1, and the initial conditions are r1(0) = −r3(0) = (−0.97000436, 0.24308753); r2(0) = (0,0); v1(0) = v3(0) = (0.4662036850, 0.4323657300); v2(0) = (−0.93240737, −0.86473146). The values are obtained from Chenciner & Montgomery (2000).
  12. ↑ Moore, Cristopher (1993), "Braids in classical dynamics" (PDF), Physical Review Letters, 70 (24): 3675–3679, Bibcode:1993PhRvL..70.3675M, doi:10.1103/PhysRevLett.70.3675, PMID 10053934
  13. ↑ Chenciner, Alain; Montgomery, Richard (2000). "A remarkable periodic solution of the three-body problem in the case of equal masses". Annals of Mathematics. Second Series. 152 (3): 881–902. arXiv:math/0011268. Bibcode:2000math.....11268C. doi:10.2307/2661357. JSTOR 2661357.
  14. ↑ Montgomery, Richard (2001), "A new solution to the three-body problem" (PDF), Notices of the American Mathematical Society, 48: 471–481
  15. ↑ Heggie, Douglas C. (2000), "A new outcome of binary–binary scattering", Monthly Notices of the Royal Astronomical Society, 318 (4): L61–L63, arXiv:astro-ph/9604016, Bibcode:2000MNRAS.318L..61H, doi:10.1046/j.1365-8711.2000.04027.x
  16. ↑ Li, Xiaoming; Liao, Shijun (December 2017). "More than six hundreds new families of Newtonian periodic planar collisionless three-body orbits". Science China Physics, Mechanics & Astronomy. 60 (12): 129511. arXiv:1705.00527. Bibcode:2017SCPMA..60l9511L. doi:10.1007/s11433-017-9078-5. ISSN 1674-7348.
  17. ↑ Li, Xiaoming; Jing, Yipeng; Liao, Shijun (13 September 2017). "The 1223 new periodic orbits of planar three-body problem with unequal mass and zero angular momentum". arXiv:1709.04775. doi:10.1093/pasj/psy057. {{cite journal}}: Cite journal requires |journal= (help)
  18. ↑ Li, Xiaoming; Liao, Shijun (2019). "Collisionless periodic orbits in the free-fall three-body problem". New Astronomy. 70: 22–26. arXiv:1805.07980. Bibcode:2019NewA...70...22L. doi:10.1016/j.newast.2019.01.003.
  19. ↑ Li, Xiaoming; Liao, Shijun (2019). "Collisionless periodic orbits in the free-fall three-body problem". New Astronomy. 70: 22–26. arXiv:1805.07980. Bibcode:2019NewA...70...22L. doi:10.1016/j.newast.2019.01.003.
  20. ↑ The 1747 memoirs of both parties can be read in the volume of Histoires (including Mémoires) of the Académie Royale des Sciences for 1745 (belatedly published in Paris in 1749) (in French):
    Clairaut: "On the System of the World, according to the principles of Universal Gravitation" (at pp. 329–364); and
    d'Alembert: "General method for determining the orbits and the movements of all the planets, taking into account their mutual actions" (at pp. 365–390).
    The peculiar dating is explained by a note printed on page 390 of the "Memoirs" section: "Even though the preceding memoirs, of Messrs. Clairaut and d'Alembert, were only read during the course of 1747, it was judged appropriate to publish them in the volume for this year" (i.e. the volume otherwise dedicated to the proceedings of 1745, but published in 1749).
  21. ↑ Jean le Rond d'Alembert, in a paper of 1761 reviewing the mathematical history of the problem, mentions that Euler had given a method for integrating a certain differential equation "in 1740 (seven years before there was question of the Problem of Three Bodies)": see d'Alembert, "Opuscules Mathématiques", vol. 2, Paris 1761, Quatorzième Mémoire ("Réflexions sur le Problème des trois Corps, avec de Nouvelles Tables de la Lune ...") pp. 329–312, at sec. VI, p. 245.
  22. ↑ Breen, Philip G.; Foley, Christopher N.; Boekholt, Tjarda; Portegies Zwart, Simon (2019). "Newton vs the machine: Solving the chaotic three-body problem using deep neural networks". arXiv:1910.07291. doi:10.1093/mnras/staa713. {{cite journal}}: Cite journal requires |journal= (help)
  23. ↑ Griffiths, David J. (2004). Introduction to Quantum Mechanics (2nd ed.). Prentice Hall. p. 311. ISBN 978-0-13-111892-8. OCLC 40251748. 
  24. ↑ 24.0 24.1 Crandall, R.; Whitnell, R.; Bettega, R. (1984). "Exactly soluble two-electron atomic model". American Journal of Physics. 52 (5): 438–442. Bibcode:1984AmJPh..52..438C. doi:10.1119/1.13650.
  25. ↑ Calogero, F. (1969). "Solution of a Three-Body Problem in One Dimension". Journal of Mathematical Physics. 10 (12): 2191–2196. Bibcode:1969JMP....10.2191C. doi:10.1063/1.1664820.
  26. ↑ Musielak, Z E; Quarles, B (2014). "The three-body problem". Reports on Progress in Physics. 77 (6): 065901. arXiv:1508.02312. Bibcode:2014RPPh...77f5901M. doi:10.1088/0034-4885/77/6/065901. ISSN 0034-4885. PMID 24913140.
  27. ↑ Florin Diacu. "The Solution of the n-body Problem", The Mathematical Intelligencer, 1996.


编者推荐

《三体》小说，作者：刘慈欣

书籍推荐

小说《三体》

《三体》是刘慈欣创作的系列长篇科幻小说，由《三体I 地球往事》、《三体Ⅱ·黑暗森林》、《三体Ⅲ·死神永生》组成，第一部于2006年5月起在《科幻世界》杂志上连载，第二部于2008年5月首次出版，第三部则于2010年11月出版。作品讲述了地球人类文明和三体文明的信息交流、生死搏杀及两个文明在宇宙中的兴衰历程。其第一部经过刘宇昆翻译后获得了第73届雨果奖最佳长篇小说奖。


集智文章

混沌与非线性：三体问题和蝴蝶效应之谜

所谓的混沌现象，其实是一种由确定的规则所产生的看起来随机的现象。混沌系统之所以看起来混乱，是因为它对初始误差非常敏感，导致我们无法准确预测混沌系统的长期行为。而初值敏感性的产生机理，就在于非线性相互作用的存在。在复杂系统中，混沌与秩序同时并存。


《自然》杂志对话刘慈欣：《三体》写作、灵感以及中国科幻

《三体》三部曲的作者刘慈欣是一位备受赞誉的中国作家。在中国，他曾多次获得银河奖（中国幻想小说界的最高荣誉奖项）。当三部曲的第一部《三体》，由刘宇昆翻译成英文并由Tor出版后，好评如潮，一举获得了2015年雨果奖最佳长篇小说奖。《自然》杂志“未来”专栏（Futures）的Preston Grassmann对话刘慈欣，讨论了关于写作、灵感以及中国科幻等问题。


本中文词条由Lincent审校，薄荷编辑，如有问题，欢迎在讨论页面留言。


本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

取自“https://wiki.swarma.org/index.php?title=三体问题&oldid=29125”