双曲空间模型
双曲空间模型(Hyperbolic space model) 在数学中,曲率为常数且为负数的空间被称为双曲空间。为了直观的表示双曲空间,数学家们开发了很多模型。
彭加莱平面
跟踪曲线 Tractrix
莱布尼茨首先提出了跟踪曲线的问题。如上面的动画所展示。考虑水平地面上有一个物体,你用一根长长的细杆推动兼或拖拉着它。细杆的长度固定,一边连接着物体,而且连接处可以自由转动,另一端则被你手牵动着。当你沿着y=0这条直线匀速直线往前走的时候,那么这个物体在水平地面上运动后形成的轨迹就被称为跟踪曲线Tractrix[1]。
下面,我们将列出这个曲线的方程,并根据这条曲线生成三维的双曲曲面。
如下图所示,根据跟踪曲线的含义,我们知道,物体的运动方向也就是曲线的切线方向,刚好与拖动的杆子(绳索)相重合,并且因为杆子的另一端始终在y=0上面滑动,所以我们可以列出方程:
根据简单的几何运算,我们知道这条曲线需要满足下面的方程:
[math]\displaystyle{ dy/dx=-\frac{y}{\sqrt{a^2-y^2}} }[/math]
其中a表示杆子的长度。当x=0时,杆子与y轴重合,于是y(0)=a为初始条件。不妨假设a=1,我们可以求解出这个微分方程。
[math]\displaystyle{ x=\mathrm{arccosh}\frac{1}{y}-\sqrt{1-y^2}. }[/math]
不过,为了后面讨论方便,我们采用曲线的弧长作为参数,来列出该曲线的参数方程。我们设从x=0点出发的曲线弧长s为自变量,那么可以知道曲线的参数方程就变为:
[math]\displaystyle{ \begin{align} &x=\mathrm{arccosh}\,e^{s}-\sqrt{1-e^{-2s}}\\ &y=e^{-s} \end{align} }[/math]
旋转跟踪曲面
让跟踪曲线绕着它的渐近线(y=0这个数轴)转一圈,形成的曲面就是一个满足曲率为-1的双曲平面,该曲面被称为Tractricoid(旋转跟踪曲面),也被称为伪球面 pseudosphere。如下图所示
我们可以用弧长以及旋转的角度作为基本参数,写出跟踪旋转曲面的参数方程:
[math]\displaystyle{ \begin{align} &x=\mathrm{arccosh}\,e^s-\sqrt{1-e^{-2s}}\\ &y=e^{-s}\mathrm{cos\,}\theta\\ &z=e^{-s}\mathrm{sin\,}\theta \end{align} }[/math]
其中s就是跟踪曲线上的物体从开始走过的弧长,[math]\displaystyle{ \theta }[/math]就是曲线从开始绕着y=0旋转的角度(如下图)。
如果我们以[math]\displaystyle{ s, \theta }[/math]为自由参数,那么它们就构成了一个描述这个旋转曲面的坐标系。
下面,我们将设法找到制约这个新曲面的度规,有关度规,请参看空间曲面。
假设我们从任意点[math]\displaystyle{ s, \theta }[/math]出发,沿着曲面行走一段小距离,这一小段既包括沿着s方向的行走,又包括了沿着[math]\displaystyle{ \theta }[/math]方向的转动。当角度旋转了[math]\displaystyle{ d\theta }[/math]之后,对应的曲面上的位移应为旋转的角度乘以旋转的半径,也就是[math]\displaystyle{ e^{-s}d\theta }[/math],这样,曲面上的一段小微元距离就应该是:
[math]\displaystyle{ dl^2=ds^2+e^{-2s}d\theta^2 }[/math]
接下来,如果我们令[math]\displaystyle{ \gamma=e^{s} }[/math],那么[math]\displaystyle{ d\gamma=e^{s}ds }[/math],于是,我们就得到:
[math]\displaystyle{ dl^2=\frac{d\gamma^2+d\theta^2}{\gamma^2}=\begin{pmatrix}d\gamma&d\theta\end{pmatrix}\begin{pmatrix}\frac{1}{\gamma^2} & 0 \\ 0 & \frac{1}{\gamma^2}\end{pmatrix}\begin{pmatrix}d\gamma\\d\theta\end{pmatrix} }[/math]
或者,也可以写作:
[math]\displaystyle{ dl=\frac{\sqrt{d\gamma^2+d\theta^2}}{\gamma} }[/math]
于是,我们就可以用新的坐标:[math]\displaystyle{ \gamma }[/math]和[math]\displaystyle{ \theta }[/math]作为坐标系,来刻画我们这个二维曲面。那么,根据空间曲面中的讨论,我们知道,这个新空间的度规矩阵可以是:
[math]\displaystyle{ \left( \begin{matrix} \frac{1}{\gamma^2} & 0\\ 0&\frac{1}{\gamma^2}\\ \end{matrix} \right) }[/math]
而这个新的空间就被称之为彭加莱平面,它是刻画二维双曲曲面的一种最常用的模型。
彭加莱平面
定义
为了刻画双曲空间,人们发明了各种各样的模型,其中彭加莱平面(Poincare plane)是我们最常用的一个。上面我们只是用跟踪曲线作为一个引子将彭加莱平面模型给引出来。下面,我们来正式引入彭加莱平面二维双曲空间模型。
设曲面M,位于二维实数空间的上半平面上,即[math]\displaystyle{ M=\{(u,v)\in R^2 | v\gt 0\} }[/math],其中u,v是曲面的坐标。对于该曲面上的任意两个切向量[math]\displaystyle{ \textbf{w}_1,\textbf{w}_2 }[/math],我们定义度规g为:
[math]\displaystyle{ g(\textbf{w}_1,\textbf{w}_2)=\frac{\textbf{w}_1\cdot \textbf{w}_2}{v^2} }[/math]
可以验证,这个度规g满足双线性的要求。这一具备该度规的曲面M被称为彭加莱平面。
当给定切向量空间中的一组基以后,我们可以将度规表示为一个矩阵(因为度规是一个双线性映射)。即:
[math]\displaystyle{ g(\textbf{x},\textbf{y})=\textbf{x}^TA\textbf{y} }[/math]
这里[math]\displaystyle{ \textbf{x},\textbf{y} }[/math]都是切向量,并在一组基下相应地展开了,A是度规g对应的矩阵。
这样,比如普通的内积对应的矩阵就是单位阵,而彭加莱平面的矩阵就是:
[math]\displaystyle{ \left( \begin{matrix} \frac{1}{v^2} & 0\\ 0&\frac{1}{v^2}\\ \end{matrix} \right) }[/math]
曲线长度
设M中有一条曲线[math]\displaystyle{ \alpha(t), t\in [a,b] }[/math],那么这条线的切向量为[math]\displaystyle{ \alpha' dt }[/math], 它的长度就是[math]\displaystyle{ dl=|\alpha'|_{hyp}dt=\frac{|\alpha'|_{euc}}{y(t)}dt }[/math],其中第一个长度[math]\displaystyle{ |\alpha'|_{hyp} }[/math]是在双曲空间下的长度,第二个长度[math]\displaystyle{ |\alpha'|_{euc} }[/math]是在欧氏空间下的长度。所以这条曲线在区间[a,b]上的长度就是:
[math]\displaystyle{ l_{hyp}=\int_a^b{\frac{\sqrt{x'(t)^2+y'(t)^2}}{y(t)}}dt }[/math]
测地线
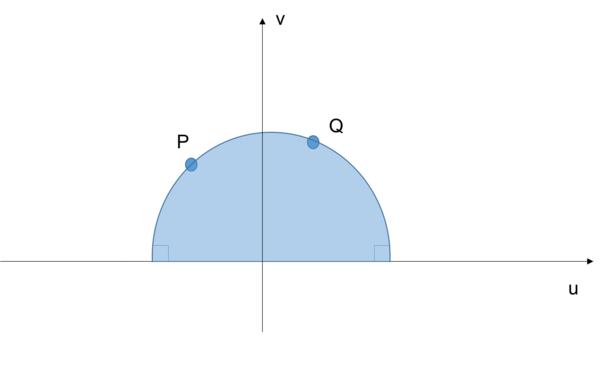
设彭加莱平面上任意两点P、Q,那么过P、Q的曲线中,双曲距离最短的一个就是链接P、Q的测地线。根据双曲空间彭加莱模型,测地线需要满足方程(参看空间曲面):[math]\displaystyle{ u''-\frac{2}{v}u'v'=0, v''+\frac{1}{v}u'^2-\frac{1}{v}v'^2=0 }[/math],最后求解可得:
[math]\displaystyle{ (u-d)^2+v^2=1/c^2 }[/math]
这是一个以u上任意点d为圆心,1/c为半径的圆,它可以由P、Q两点的坐标确定下来。这就是彭加莱平面上的测地线,如下图。
当P、Q两点位于垂直于X轴的同一条直线上的时候,穿过P、Q的测地线就是这条垂直于X轴的竖直线,它可以看作是一个半径为无穷大的圆。
双曲距离
下面,我们考察空间中任意两点P(x1,y1)、Q(x2,y2)之间的距离。
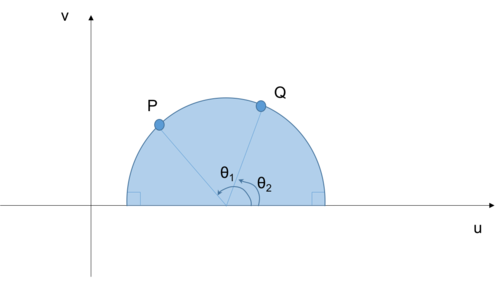
我们知道,PQ之间的双曲距离应该是连接P、Q两点的中心在x轴上面的半圆所对应的弧长。但是,我们并不能直接用这段弧长在欧氏空间下的弧长公式来计算,这是因为空间的度规不是欧氏的而是双曲的,因此我们应该沿着这段弧长对双曲度规做积分。我们设P、Q两点中心在x轴上的半圆的圆心O在[math]\displaystyle{ x_0 }[/math],半径为r,那么我们可以写出这个半圆所满足的参数方程为:
[math]\displaystyle{ x=x_0+r \mathrm{cos\,}\theta,y=r \mathrm{sin\,}\theta }[/math]
其中[math]\displaystyle{ x_0=\frac{x_2^2-x_1^2+y_2^2-y_1^2}{2(x_2+x_1)} }[/math],以及[math]\displaystyle{ r=\sqrt{y_1^2+\frac{(x_1-x_2)^2-y_1^2+y_2^2)^2}{4(x_1-x_2)^2}} }[/math]
沿这条曲线做度规的积分得到,距离:
[math]\displaystyle{ d_{hyp}(P,Q)=\int_{\theta_1}^{\theta_2}\frac{\sqrt{x'(\theta)^2+y'(\theta)^2}}{y}d\theta=\int_{\theta_1}^{\theta_2}\frac{1}{\mathrm{sin\,}\theta}d\theta=\log\frac{\tan{\theta_2/2}}{\tan{\theta_1/2}} }[/math]
其中,[math]\displaystyle{ \theta_1 }[/math]为P到O的直线与x轴的夹角,[math]\displaystyle{ \theta_2 }[/math]为Q到O的直线与x轴的夹角,如下图:
进一步,如果我们设P对应的二维坐标写成复数z,而Q则写成复数z'的形式,那么将上式化简,可得到:
[math]\displaystyle{
d_{hyp}(P,Q)=\log\frac{|z-\bar{z}'|+|z-z'|}{|z-\bar{z}'|-|z-z'|}
}[/math]
其中,[math]\displaystyle{ z=x_1+y_1i,z'=x_2+y_2i,\bar{z}'=x_2-y_2i }[/math]
等距变换
在一般曲面的几何中,人们一般关心这个空间中的等距变换。顾名思义,设[math]\displaystyle{ \Gamma }[/math]是一个将M上的点映射到另一个点的映射,那么如果它是一个等距变换的话,那么对于M上的任意两点有:
[math]\displaystyle{ d(P,Q)=d(\Gamma(P),\Gamma(Q)) }[/math]
也就是说,这种几何变换可以保持距离。我们知道,刚体在欧氏空间中运动的时候,物体的形状就保持不变。因此,等距变换就相当于是让几何形体做刚体运动。
下面,我们可以看几个等距变换的实例:
同位变换 Homotheties
所谓的同位变换,是指满足下列关系的变换:([math]\displaystyle{ \phi(x,y)=(\lambda x,\lambda y) }[/math]),其中[math]\displaystyle{ \lambda }[/math]是变换中的参数。这种变换相当于以原点(0,0)为中心,向外放大几何图形。为什么说这是一种等距变换呢?这是因为对于任意的曲线[math]\displaystyle{ \gamma(t) }[/math],那么它上面的所有店点经过变换[math]\displaystyle{ \phi }[/math]之后映射到了新的曲线,那么这条新曲线的长度为:
[math]\displaystyle{ l_{hyp}(\phi(\gamma))=\int_a^b\frac{\sqrt{\lambda^2x'(t)^2+\lambda^2y'(t)^2}}{\lambda y(t)}dt=\int_a^b\frac{\sqrt{x'(t)^2+y'(t)^2}}{y(t)}dt=l_{hyp}(\gamma) }[/math]
由此可见,它并不改变曲线的长度。因此,对于任意两点之间的测地线来说,这个结论也满足,所以距离在这个变换下保持不变。
标准倒置变换
下面,让我们再来看一个等距变换的实例。这就是倒置变换,对于彭加莱平面上的任意点(x,y),等距变换[math]\displaystyle{ \phi }[/math]定义为:
[math]\displaystyle{ \phi(x,y)=\left(\frac{x}{x^2+y^2},\frac{y}{x^2+y^2}\right) }[/math]
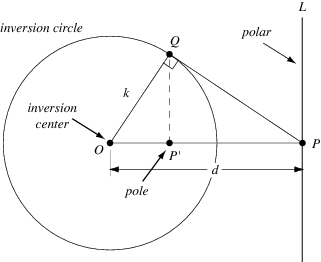
在几何上,这个变换相当于对点(x,y)沿着单位圆做倒置(参见下面的讨论)。
如图所示,所谓P与P'关于圆O互为倒置,是指[math]\displaystyle{ |OP|\cdot |OP'|=r^2 }[/math],其中r为圆的半径。
为什么说这个变换是一个等距变换呢?我们仍然用任意一条曲线[math]\displaystyle{ \gamma(t) }[/math]来说明。假设曲线[math]\displaystyle{ \gamma: t \mapsto (x_1(t),y_1(t)), a\leq t\leq b }[/math]
这里:
[math]\displaystyle{ x_1(t)=\frac{x(t)}{x(t)^2+y(t)^2}, y_1(t)=\frac{y(t)}{x(t)^2+y(t)^2} }[/math]
于是,它们的导数分别是:
[math]\displaystyle{ x'_1(t)=\frac{(y(t)^2-x(t)^2)x'(t)-2x(t)y(t)y'(t)}{(x(t)^2+y(t)^2)^2}, y'_1(t)=\frac{(y(t)^2-x(t)^2)y'(t)-2x(t)y(t)x'(t)}{(x(t)^2+y(t)^2)^2} }[/math]
将这两个式子化简,再相加到一起,得到:
[math]\displaystyle{
x'_1(t)^2+y'_1(t)^2=\frac{x'(t)^2+y'(t)^2}{(x(t)^2+y(t)^2)^2}
}[/math]
于是,就有:
[math]\displaystyle{ l_{hyp}(\phi(\gamma))=\int_a^b\frac{\sqrt{x'_1(t)^2+y'_1(t)^2}}{y_1(t)}dt=\int_a^b\frac{\sqrt{x'(t)^2+y'(t)^2}}{y(t)}dt=l_{hyp}(\gamma) }[/math]
所以,这是一个保距变换。
水平平移
设任意点(x,y),它沿水平方向平移x0定义为变换:
[math]\displaystyle{ \phi(x,y)=(x+x_0,y) }[/math]
容易验证,这种变换也是保距变换。
一般形式
我们已经看到了三种保距变换:同位、倒置和水平平移。我们知道,Poincare平面模型中的点(x,y)可以表达成复数z=x+yi,那么同位变换就相当于复数映射[math]\displaystyle{ z\mapsto \lambda z }[/math] ,倒置操作就相当于变换:[math]\displaystyle{ z\mapsto \frac{z}{|z|^2}=\frac{1}{\bar{z}} }[/math],这里[math]\displaystyle{ \bar{z} }[/math]是z的共轭复数。而平移变换则相当于:[math]\displaystyle{ z\mapsto z+x_0 }[/math],所以它们都可以写成复数的运算。一般的,对于任意一种保距变换来说,它都可以表达成复数变换公式:
[math]\displaystyle{ z\mapsto \frac{az+b}{cz+d}, }[/math]
或者:
[math]\displaystyle{ z\mapsto \frac{c\bar{z}+d}{a\bar{z}+b} }[/math]
这里的[math]\displaystyle{ a,b,c,d\in R }[/math]都是常数,且满足:
[math]\displaystyle{ ad-bc=1 }[/math]
反过来讲,对于任意的参数a,b,c,d上述两式都可以对应彭加莱平面中的等距变换。
圆
在欧氏空间中,我们将圆定义为到某一个定点P0距离相同的所有点的集合。
类似地,我们可以在双曲空间种定义圆为到某一个定点P0双曲距离相同的所有点的集合。那么这个双曲空间中的圆在Poincare平面空间中长什么样子呢?
我们设固定点P0的复数表示为z=a+bi, 动点P的复数表示为z'=x+yi,那么根据上述推出来的距离公式,我们有:
[math]\displaystyle{ \frac{1+\frac{|z-z'|}{|z-\bar{z'}|}}{1-\frac{|z-z'|}{|z-\bar{z'}|}}=e^R }[/math]
其中R就是这个圆的半径,[math]\displaystyle{ c=\frac{e^R+1}{e^R-1} }[/math]。将坐标代入,进行整理就会得到关于x和y的一个方程:
[math]\displaystyle{ \left(x-\frac{a-ac^2}{1-c^2}\right)^2+\left(y-\frac{b+bc^2}{1-c^2}\right)^2=\left(\frac{2bc}{1-c^2}\right)^2 }[/math]
因此,从方程形式上不难看出,这在欧氏空间的笛卡尔坐标系下,是一个以[math]\displaystyle{ (\frac{a-ac^2}{1-c^2},\frac{b+bc^2}{1-c^2}) }[/math]为圆心,以[math]\displaystyle{ \left(\frac{2bc}{1-c^2}\right) }[/math]为半径的圆。所以说,双曲空间下的圆在彭加莱平面的表象下也是圆。
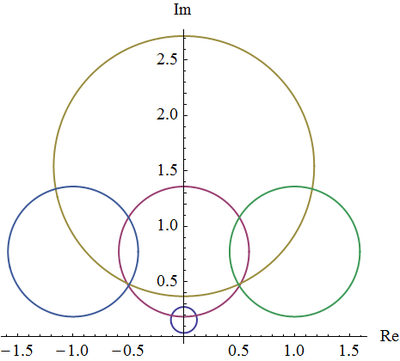
我们可以让圆心P0取不同的位置,利用上述方程画出这些圆如下:
其中不同的颜色曲线对应了不同中心点P0的双曲空间中的圆,它们的半径都是1,这些圆的圆心坐标分别为(0,0.1),(0,0.5),(0,1),(1,0.5),(-1,0.5)。这些圆虽然双曲半径都是1,但是它们在欧氏空间下的表观形状会大小都不一样。由图可见,中心点越往上,它相应的表观半径也越大。在同一个水平方向上,圆的表观形状相同。
另外一个有趣的事实是,双曲空间中的圆的圆心并不在表观圆的圆心上,而且这种偏离程度会随着y坐标轴的升高而增大。
彭加莱圆盘
虽然彭加莱平面可以很好地模型化双曲空间,但是它也仍然存在着很多弊端。为了避免这些弊端,我们可以再建立一种模型,这被称为彭加莱圆盘(Poincare disk,如上图)。为了得到彭加莱圆盘,我们首先要在(0,-1)的位置上,以[math]\displaystyle{ \sqrt{2} }[/math]为半径做一个圆。之后,我们就可以将彭加莱平面上的所有点都对这个圆做倒置inversion操作,然后再对y=0这个数轴做轴对称操作。
我们不妨将这一变换称为J,然后看一些特殊的点在J的作用下映射到了哪里。我们先看原点(0,0)。它到圆心的距离为1,所以它的倒置操作的对应像应该在(0,1)这个位置上,把它沿着y=0轴翻转一下就得到了(0,-1),所以(0,0)映射到了(0,-1)。我们再看看(-1,0)和(1,0),不难看出它们都在这个J的映射作用下保持不变。而无穷大会对应到(0,1)这个点上。不难验证,所有彭加莱平面上的点在J的作用下之后形成了一个以原点为中心的单位圆。这个圆就被称为彭加莱元。
如果我们用复数z来描述彭加莱平面上的所有点,那么变换J就可以写为下面这样的函数:
[math]\displaystyle{ J(z)=\frac{i z+1}{z+i} }[/math]
我们不妨验证一下,将[math]\displaystyle{ z=0 }[/math]代入上式就得到,[math]\displaystyle{ J(0)=-i }[/math],这和上面得到的计算结果是一模一样的。
实质上这个变换的本质就是在于将彭加莱平面的x轴沿着i这个点为中心卷起来,形成了彭加莱圆盘的外围的圆。
度规
在彭加莱圆盘上,对于任意点P(x,y),该点的任意两个向量为[math]\displaystyle{ \textbf{u},\textbf{v} }[/math],则度规定义为:
[math]\displaystyle{ g(\textbf{u},\textbf{v})=\frac{2\textbf{u}\cdot \textbf{v}}{1-x^2-y^2} }[/math] 其中g为P点处的度规,d(u,v)为欧氏空间下的两向量的内积。
如果用复数来表示坐标的话,那么度规为:
[math]\displaystyle{ g(\textbf{u},\textbf{v})=\frac{2\textbf{u}\cdot \textbf{v}}{1-|z|^2} }[/math]
我们也可以根据映射J,以及彭加莱平面的度规来计算出彭加莱圆盘的度规:
[math]\displaystyle{ ds^2=\frac{4dx^2+4dy^2}{(1-x^2-y^2)^2}=\begin{pmatrix}dx&dy\end{pmatrix}\begin{pmatrix}\frac{1}{(1-x^2-y^2)^2}&0\\0&\frac{1}{(1-x^2-y^2)^2}\end{pmatrix}\begin{pmatrix}dx\\dy\end{pmatrix} }[/math]
或者:
[math]\displaystyle{ ds=\frac{2\sqrt{dx^2+dy^2}}{1-x^2-y^2} }[/math]
由于彭加莱圆盘是一个圆,所以我们用极坐标描述会更方便,那么,在极坐标[math]\displaystyle{ (\theta,r) }[/math]下的度规为:
[math]\displaystyle{ ds^2=\frac{d\theta^2+r^2dr^2}{(1-r^2)^2}=\begin{pmatrix}d\theta&dr\end{pmatrix}\begin{pmatrix}\frac{1}{(1-r^2)^2}&0\\0&\frac{1}{(1-r^2)^2}\end{pmatrix}\begin{pmatrix}d\theta\\dr\end{pmatrix} }[/math]
距离计算
由于映射[math]\displaystyle{ J: z\mapsto \frac{iz+1}{z+i} }[/math]是保距的,对于任意的彭加莱平面上的两点P,Q, 它们对应的复数分别为:z,z',被这个映射映到彭加莱圆盘上,则在圆盘上的像J(P)和J(Q)之间的距离ddisk(J(P),J(Q)),应该等于=dplane(P,Q),而我们知道
[math]\displaystyle{ d_{plane}(P,Q)=\log \frac{|z-\bar{z}'|+|z-z'|}{|z-\bar{z}'|-|z-z'|} }[/math]
设J(P)和J(Q)对应的复数分别为w和w',这样,根据映射我们可以反解出:
[math]\displaystyle{ z=\frac{1-wi}{w-i},z'=\frac{1-w'i}{w'-i},\bar{z}'=\frac{1+\bar{w}'i}{\bar{w}'+i} }[/math]
将其带入可以得到
[math]\displaystyle{ d_{disk}(J(P),J(Q))=d_{plane}(P,Q)=\log{\frac{1+s}{1-s}} }[/math]
其中,[math]\displaystyle{ s=\frac{|w-w'|}{|1-w\bar{w'}|} }[/math]
这就是彭加莱圆盘中的两点距离的表达式。特别的,当Q是彭加莱圆盘的圆心的时候,w'=0,则距离表达式为:
[math]\displaystyle{ d_{disk}(0,w)=\log{\frac{1+|w|}{1-|w|}} }[/math]
其中,w为另一个点对应的复数。
测地线
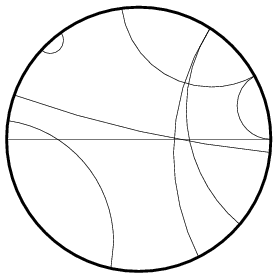
在Poincare圆盘中,测地线为与圆盘外围的圆相垂直的圆弧,包括穿越圆心的直线,如上图。
因为从Poincare平面到Poincare圆盘的映射为一个等距映射,所以它将Poincare平面上的测地线也映射成为Poincare圆盘上的测地线。又因为在平面中的测地线是垂直于x轴的圆,所以在圆盘上,测地线为垂直于边界圆的圆。
等距变换
所有的彭加莱圆盘上的等距变换都可以用下列式子来表示:
[math]\displaystyle{ \phi(z)=\frac{\alpha z+\beta}{\bar{\beta} z+\bar{\alpha}}, or, \phi(z)=\frac{\alpha \bar{z}+\beta}{\bar{\beta}\bar{z}+\bar{\alpha}} }[/math]
其中,[math]\displaystyle{ \alpha,\beta }[/math]需要满足:
[math]\displaystyle{ |\alpha|^2-|\beta|^2=1 }[/math]
圆
如果我们设w=a+bi, w'=x+yi, 圆的半径为r,则根据两点之间的距离公式,有:
[math]\displaystyle{ \log{\frac{1+|w'-w|}{|1-w\bar{w'}|}}=r }[/math]
反解出关于x和y的方程:
[math]\displaystyle{ 1-a^2 c^2-b^2 c^2+\left(-2 a+2 a c^2\right) x+\left(a^2+b^2-c^2\right) x^2+\left(-2 b+2 b c^2\right) y+\left(a^2+b^2-c^2\right) y^2=0 }[/math]
进一步化简可得:
[math]\displaystyle{ \left(x-\frac{ac^2-a}{c^2-a^2-b^2}\right)^2+\left(y-\frac{bc^2-b}{c^2-a^2-b^2}\right)^2=\left(\frac{\left(-1+a^2+b^2\right) c}{\left(a^2+b^2-c^2\right)}\right)^2 }[/math]
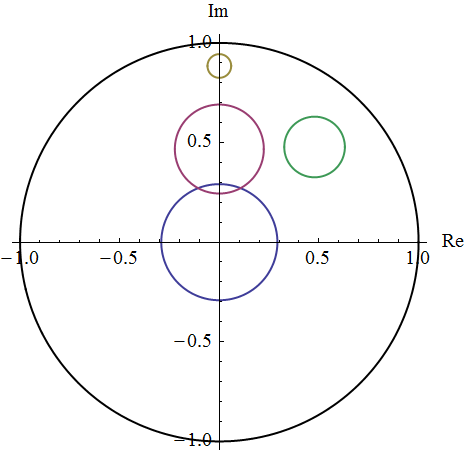
其中[math]\displaystyle{ c=\frac{e^r+1}{e^r-1} }[/math]。可以看出,这是一个圆的方程。所以,在彭加莱圆盘中的双曲圆也是欧几里德空间中的圆。下面,我们画出一些圆的图形,如下:
最外圈的黑色的圆为彭加莱圆盘。其它的圆均是半径为0.6的圆,但是它们的圆心(a,b)位于不同的位置,圆心分别为:(0,0),(0,0.5),(0,0.9)以及(0.5,0.5),我们可以看到,在双曲空间中,圆心并不位于圆的正中心,越靠近边缘,圆心越往外靠近边缘。而且,圆越靠近边缘,圆的表观大小也会变小。
圆的周长和面积
虽然彭加莱圆盘中的双曲圆还表现为圆,但是它的周长与面积的计算则与欧氏空间中完全不同。这是因为,当我们计算周长或者面积的时候,我们实际上在计算曲线或者区域的积分,所以我们需要考虑双曲空间中的度规的影响,下面我们就来以圆心为(0,0),双曲半径为R(对应的欧几里德空间中的圆的表观半径为:[math]\displaystyle{ r=\frac{e^R-1}{e^R+1} }[/math]的圆为例来计算圆的周长和面积。
首先,周长计算应为:
[math]\displaystyle{ C((0,0),R)=\int_0^{2\pi}\frac{2r}{1-r^2}d\theta=2\pi \sinh(R) }[/math]
类似地,圆的面积为:
[math]\displaystyle{ A((0,0),R)=\int\int_{|z|\lt r}\frac{4}{(1-|z|^2)^2}d\sigma=\int_0^{R}dr\int_0^{2\pi}d\theta \frac{4r}{(1-r^2)^2}=2\pi(\cosh{R}-1) }[/math]
由此我们可以看出,无论是周长还是面积,它们都与半径R呈现出指数行的增长(注意到[math]\displaystyle{ \sinh(x)=\frac{e^x-e^{-x}}{2},\cosh(x)=\frac{e^x+e^{-x}}{2} }[/math]),所以双曲空间是一个沿半径增长非常快的空间。到达圆盘边缘的区域就已经增长到相当的空间区域了。这就是双曲空间的显著特征。
不难用双曲空间中的圆方程证明,对于中心不在原点的圆,其直径和面积仍然是上述表达式。虽然我们不能将圆在不同位置平移,但是双曲空间的均匀性导致了圆的周长和面积是处处相等的。
扩展的彭加莱圆盘
在彭加莱圆盘模型中,我们要时刻警惕,虽然整个空间沿着中心对称,但是从原点到任意一个点的表观距离并不等于双曲距离。如果设表观的欧氏距离为re,双曲距离为rh,则这二者之间满足如下关系:
[math]\displaystyle{ r_e=\tanh{r_h/2} }[/math]
因此,为了让表观距离和实际的双曲距离一致,我们可以建立一个新的模型,这就是扩展的彭加莱模型,使得任意点到中心的距离刚好等于双曲距离。假设原始坐标系(彭加莱圆盘)上任意点的极坐标为[math]\displaystyle{ (r,\theta) }[/math],而新空间下该点的极坐标为[math]\displaystyle{ (r',\theta') }[/math],则存在关系:
[math]\displaystyle{ r'=2\tanh^{-1}{r},\theta'=\theta }[/math]
则这个新的空间[math]\displaystyle{ (r',\theta) }[/math]即是扩展的彭加莱圆盘。
我们知道由于[math]\displaystyle{ \tanh(x) }[/math]函数是一个S型函数,在x趋近于无穷大的时候,该函数值趋于1。所以,彭加莱圆盘具有1单位大小的半径。而在扩展的彭加莱圆盘中,该空间的圆半径为无穷大。因而,在彭加莱圆盘表示中,靠近边缘的点被极度地压缩了。而在扩展的模型中,就不会存在这种被极度压缩的现象。
度规
我们知道,在彭加莱圆盘模型中,一小段微元可以写成极坐标形式的度规为:
[math]\displaystyle{ ds^2=4\frac{dr^2+r^2d\theta^2}{(1-r^2)^2}=4(dr,d\theta)\begin{pmatrix}1 & 0 \\ 0 & \frac{r^2}{(1-r^2)^2}\end{pmatrix} \begin{pmatrix} dr\\ d\theta\end{pmatrix} }[/math]
我们将坐标变换[math]\displaystyle{ r=\tanh(r'/2),\theta=\theta' }[/math]代入上式,并注意到:[math]\displaystyle{ dr^2=\frac{dr'^2}{4\cosh^2(r'/2)} }[/math],则得到:
[math]\displaystyle{ ds^2=4\frac{\frac{1}{4\cosh(r'/2)} dr'^2+\tanh^2(r'/2)d\theta'^2}{(1-\tanh^2(r'/2))^2}=dr'^2+\sinh^2(r')d\theta'^2 }[/math]
或者,可以写为:
[math]\displaystyle{ ds=\sqrt{dr'^2+\sinh^2(r')d\theta'^2} }[/math]
任意两点距离公式
设任意两点P、Q,它们在扩展彭加莱圆盘中的极坐标为:[math]\displaystyle{ (r,\theta) }[/math], [math]\displaystyle{ (r',\theta') }[/math],设它们之间的双曲距离为x,则:
[math]\displaystyle{ \cosh{x}=\cosh(r)\cosh(r')-\sinh(r)\sinh(r')\cos(\Delta \theta) }[/math]
其中,[math]\displaystyle{ \Delta \theta=\pi-|\pi-|\theta-\theta'|| }[/math]
这与彭加莱圆盘中的距离公式一致,下面我们给出证明。
证明:
首先根据彭加莱圆盘中的距离公式:
[math]\displaystyle{ x=\log\frac{1+s}{1-s}, s=\frac{|w-w'|}{1-w\bar{w'}} }[/math] ,并设w,w'在彭加莱圆盘中的极坐标分别为:[math]\displaystyle{ (R,\theta),(R',\theta') }[/math]
则 [math]\displaystyle{ s=\sqrt{\frac{R^2+R'^2-2RR'\cos\Delta\theta}{1+R^2R'^2-2RR'\cos\Delta\theta}} }[/math]
而: [math]\displaystyle{ \cosh(x)=\frac{\exp(x)+\exp(-x)}{2}=\frac{1}{2}\left(\frac{1+s}{1-s}+\frac{1-s}{1+s}\right)=\frac{1+s^2}{1-s^2} }[/math]
将s代入,则得到:
[math]\displaystyle{ \cosh(x)=\frac{1+R^2+R'^2+R^2R'^2-4RR'\cos\theta}{(1-R^2)(1-R'^2)} }[/math]
另一方面,将[math]\displaystyle{ r=\tanh(R/2),r'=\tanh(R'/2) }[/math]代入下面公式:
[math]\displaystyle{ \cosh(x)=\cosh(r)\cosh(r')-\sinh(r)\sinh(r')\cos(\Delta \theta)=\frac{1+R^2}{1-R^2}\cdot \frac{1+R'^2}{1-R'^2}-4 \frac{RR'\cos\Delta\theta}{(1-R^2)(1-R'^2)} }[/math]
故而两者相等。
近似表达式
当r和r'都很大,而且x也较大的时候,我们有近似公式:
[math]\displaystyle{ x\approx r+r'+2\log{\sin(\Delta\theta/2)} }[/math]
当[math]\displaystyle{ \Delta\theta/2) }[/math]很小的时候,
[math]\displaystyle{ x\approx r+r'+2\log{\Delta\theta/2} }[/math]
圆
根据彭加莱圆模型与扩展模型中极坐标之间的关系:
[math]\displaystyle{ r_e=\tanh(r_h/2) }[/math]
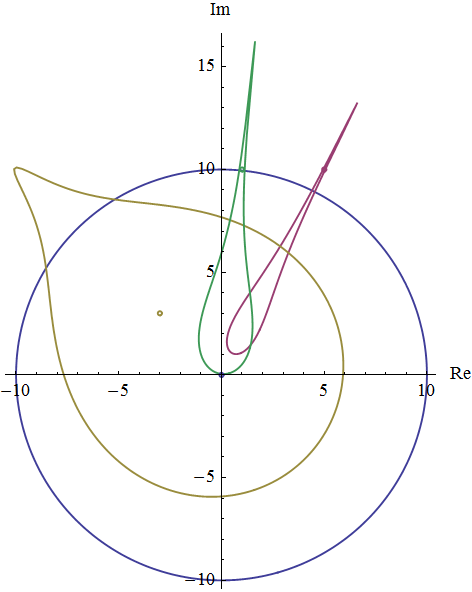
又知道彭加莱圆模型中以某点为中心的圆方程,代入上述坐标变换公式,就能得到扩展模型中的圆。不难从图形上看出,这个圆被严重扭曲、拉伸了。
这些圆中心的坐标分别为:(0,0) 蓝色, (5,10) 紫色,(-3,3) 黄色,(1,10) 绿色,这些圆的半径都是10。我们看到,越远离坐标中心,圆的扭曲也越厉害。
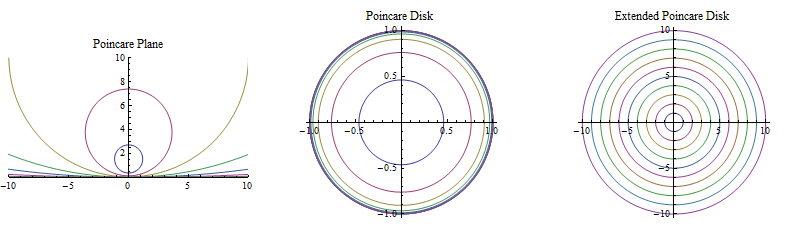
各个模型的比较
上述文章介绍了三种双曲平面的表示模型:彭加莱平面、彭加莱圆盘以及扩展的彭加莱圆盘。我们可以通过下图来比较这三种模型:
这是在扩展彭加莱圆盘模型中的一组同心圆,也就是每一条曲线都是以彭加莱圆盘中的坐标原点为中心,到圆心的双曲距离分别为1,2,……,10的圆。当把这组曲线画在彭加莱平面中的时候,我们就看到了一组以(0,1)为中心的双曲空间中的圆曲线(在彭加莱平面中,双曲圆的中心并不是欧氏圆的中心),而在彭加莱圆盘模型中,这组圆从里往外变得越来越紧密,这说明彭加莱圆盘越到外围空间越紧密。
参考文献
- Francis Bonahon: Low-dimensional geometry - From Euclidean Surfaces to Hyperbolic Knots, American Mathematical Society, 1995
- John Stillwell: Geometry of Surfaces, Springer-Verlag New York, 1992
- Riccardo Benedetti, Carlo Petronio: Lectures on Hyperbolic Geometry, Springer-Verlag Berlin Hamberg, 1992
- Wikipedia: https://en.wikipedia.org/wiki/Tractrix
另见
编者推荐
集智课程
HGCN:双曲嵌入下的图卷积网络
本课程来自集智第 37 期图网络论文解读活动。本文在诸多前人工作基础上,结合图网络和双曲嵌入的优势,提出了双曲嵌入(hyperbolic embedding)下的图卷积网络,即HGCN. 在这种网络结构下,普通的神经网络操作通过增加曲率参数推广到双曲空间,优化也在双曲空间中进行。HGCN在诸多的数据集上, 在节点分类和连边预测等任务上取得了比GCN类算法更好的效果,成为图网络算法的有力扩展。
集智文章
本中文词条由Jake翻译,薄荷编辑,如有问题,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。