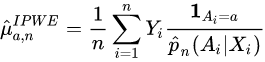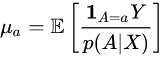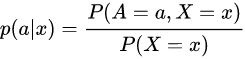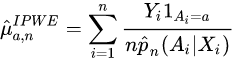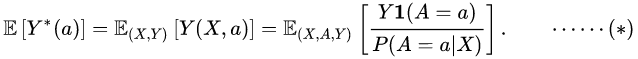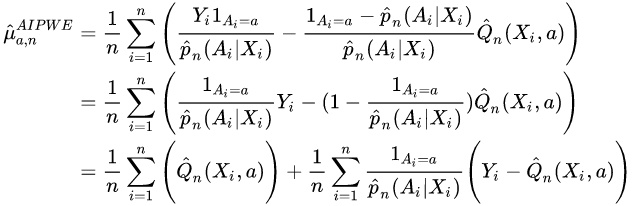双稳健

Inverse probability weighting is a statistical technique for calculating statistics standardized to a pseudo-population different from that in which the data was collected. Study designs with a disparate sampling population and population of target inference (target population) are common in application. There may be prohibitive factors barring researchers from directly sampling from the target population such as cost, time, or ethical concerns. A solution to this problem is to use an alternate design strategy, e.g. stratified sampling. Weighting, when correctly applied, can potentially improve the efficiency and reduce the bias of unweighted estimators.

One very early weighted estimator is the Horvitz–Thompson estimator of the mean. When the sampling probability is known, from which the sampling population is drawn from the target population, then the inverse of this probability is used to weight the observations. This approach has been generalized to many aspects of statistics under various frameworks. In particular, there are weighted likelihoods, weighted estimating equations, and weighted probability densities from which a majority of statistics are derived. These applications codified the theory of other statistics and estimators such as marginal structural models, the standardized mortality ratio, and the EM algorithm for coarsened or aggregate data.

Inverse probability weighting is also used to account for missing data when subjects with missing data cannot be included in the primary analysis. With an estimate of the sampling probability, or the probability that the factor would be measured in another measurement, inverse probability weighting can be used to inflate the weight for subjects who are under-represented due to a large degree of missing data.

【翻译】逆概率加权是一种统计技术，用于计算标准化与收集数据的伪总体不同的统计量。研究设计与不同的抽样总体和总体的目标推断(目标总体)是常见的应用。可能存在阻碍研究人员直接从目标人群中采样的因素，如成本、时间或伦理问题。解决这个问题的方法是使用另一种设计策略，例如分层抽样。如果正确使用加权，可能会提高效率，减少未加权估计量的偏差。

一个非常早期的加权估计是霍维茨汤姆森估计量的均值估计。当抽样概率已知时，从目标总体中抽取抽样总体，然后利用这个概率的逆值对观测值进行加权。这种方法已经在各种框架下推广到统计学的许多方面。特别是，有加权的可能性，加权的估计方程，和加权的概率密度，其中大多数统计数据都是从中导出的。这些应用编纂了其他统计和估计理论，例如边际结构模型、标准死亡率和用于粗化或汇总数据的 EM 算法。

当缺失数据的受试者不能被包括在主要分析中时，逆概率加权也被用来解释缺失数据。通过对抽样概率的估计，或该因子在另一测量中被测量的概率，逆概率加权可以用来为由于大量数据缺失而代表性不足的受试者增加权重。

Inverse Probability Weighted Estimator (IPWE)

The inverse probability weighting estimator can be used to demonstrate causality when the researcher cannot conduct a controlled experiment but has observed data to model. Because it is assumed that the treatment is not randomly assigned, the goal is to estimate the counterfactual or potential outcome if all subjects in population were assigned either treatment.

Suppose observed data are  drawn i.i.d (independent and identically distributed) from unknown distribution P, where

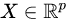• covariates
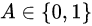• are the two possible treatments.
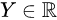• response
• We do not assume treatment is randomly assigned.

The goal is to estimate the potential outcome, , that would be observed if the subject were assigned treatment . Then compare the mean outcome if all patients in the population were assigned either treatment: . We want to estimate  using observed data .

【翻译】

当研究人员不能进行对照实验而只能通过观测数据建立模型时，逆概率加权估计可以用来证明因果关系。

因为假设治疗不是随机分配的，目标是估计反事实或潜在的结果，如果所有受试者在人口中被分配任何一种治疗。

假设观测数据是从未知分布 P 中提取 i.i.d (独立且同分布) ，其中协变量是两种可能的处理方法。

• 协变量
• 是两个可能的干预
• 反应

我们不认为治疗是随机分配的。

目标是估计潜在的结果，，这将被观察到，如果受试者被分配治疗。然后比较平均结果，如果所有患者在人群中被分配任一治疗: 。我们想利用观测数据进行估计。

Estimator Formula[edit]

Constructing the IPWE[edit]

1. where
2. construct  or  using any propensity model (often a logistic regression model)
3. 

With the mean of each treatment group computed, a statistical t-test or ANOVA test can be used to judge difference between group means and determine statistical significance of treatment effect.

【翻译】

构建 IPWE

1. where
2. 构建  or  使用任意一个倾向得分模型l (通常是一个逻辑回归模型)
3. 

通过计算各治疗组的平均值，采用统计 t 检验或方差分析(ANOVA)检验可以判断各组平均值的差异，并确定治疗效果的统计学意义

Assumptions[edit]

Recall the joint probability model (X,A,Y)~P for the covariate X , action A, and response Y. If  X and  A are known as x and a, respectively, then the response Y(X=x,A=a)=Y(x=a)has the distribution

We make the following assumptions.

• (A1) Consistency: Y=Y*(A)
• (A2) No unmeasured confounders: 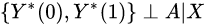. More formally, for each bounded and measurable functions  f and g, 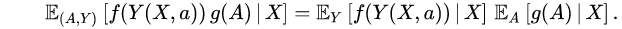This means that treatment assignment is based solely on covariate data and independent of potential outcomes.
• (A3) Positivity: 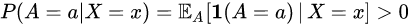 for all  a and x.

【翻译】

假设

回想一下协变量 X，行为 A 和响应 Y 的联合概率模型(X，A，Y) ~ P。如果 X 和 A 分别被称为 x 和 a，那么响应 Y (X = x，A = a) = Y (x = a)具有分布

我们使得以下假设成立

• (A1) 一致性: Y=Y*(A)
• (A2) 无未观测到的混杂因素: 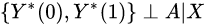. 更一般的，对于每个有界可测函数f和g都有 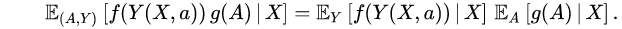这意味着治疗分配完全基于协变量数据，独立于潜在的结果。
• (A3) 积极性: 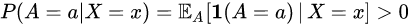 f对于所有a和x.

Formal derivation[edit]

Under the assumptions (A1)-(A3), we will derive the following identities

The first equality follows from the definition and (A1). For the second equality, first use the iterated expectation to write

By (A3),  almost surely. Then using (A2), note that

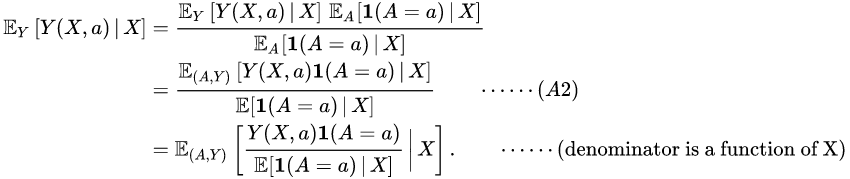Hence integrating out the last expression with respect to  and noting that  almost surely, the second equality in  follows.

【翻译】

在假设(A1)-(A3)下，我们将导出以下恒等式

第一个等式来自定义和(A1)。对于第二个等式，首先使用迭代的期望值来写

通过(A3) ，几乎可以肯定。然后使用(A2) ，注意

因此结合了最后一个表达式，几乎可以肯定，下面第二个等式。

Limitations[edit]

The Inverse Probability Weighted Estimator (IPWE) can be unstable if estimated propensities are small. If the probability of either treatment assignment is small, then the logistic regression model can become unstable around the tails causing the IPWE to also be less stable.

【翻译】

反概率加权估计(IPWE)可能是不稳定的，如果估计的倾向性很小。如果任何一种治疗分配的可能性都很小，那么 Logit模型模型可能在尾部周围变得不稳定，导致 IPWE 也变得不那么稳定。

Augmented Inverse Probability Weighted Estimator (AIPWE)

An alternative estimator is the augmented inverse probability weighted estimator (AIPWE) combines both the properties of the regression based estimator and the inverse probability weighted estimator. It is therefore a 'doubly robust' method in that it only requires either the propensity or outcome model to be correctly specified but not both. This method augments the IPWE to reduce variability and improve estimate efficiency. This model holds the same assumptions as the Inverse Probability Weighted Estimator (IPWE).

【翻译】

增广逆概率加权估计(AIPWE)是一种结合了基于回归估计和逆概率加权估计性质的替代估计。因此，它是一种“双稳健”方法，因为它只需要正确指定倾向或结果模型，而不是两者兼而有之。该方法增强了 IPWE，降低了变异性，提高了估计效率。这个模型拥有与反概率加权估计(IPWE)相同的假设。

Estimator Formula

With the following notations:

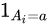1. is an indicator function if subject i is part of treatment group a (or not).
2. Construct regression estimator 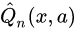 to predict outcome Y based on covariates X and treatment A , for some subject i. For example, using ordinary least squares regression.
3. Construct propensity (probability) estimate 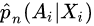. For example, using logistic regression.
4. Combine in AIPWE to obtain

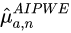
【翻译】

附有以下注释:

如果受试者 i 属于 a 组(或不属于 a 组) ，则属于指示函数。

构建回归估计器，根据协变量 x 和治疗方案 a，对某些受试者 i，预测 Y 的结果。例如，使用一般最小平方法回归。

构建倾向(概率)估计，例如，使用 Logit模型。

在 AIPWE 中组合以获得

Interpretation and "double robustness"

The later rearrangement of the formula helps reveal the underlying idea: our estimator is based on the average predicted outcome using the model (i.e.: 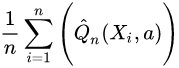). However, if the model is biased, then the residuals of the model will not be (in the full treatment group a) around 0. We can correct this potential bias by adding the extra term of the average residuals of the model (Q) from the true value of the outcome (Y) (i.e.: 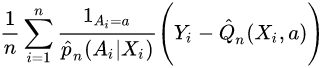). Because we have missing values of Y, we give weights to inflate the relative importance of each residual (these weights are based on the inverse propensity, a.k.a. probability, of seeing each subject observations) (see page 10 in ).

The "doubly robust" benefit of such an estimator comes from the fact that it's sufficient for one of the two models to be correctly specified, for the estimator to be unbiased (either  or , or both). This is because if the outcome model is well specified then its residuals will be around 0 (regardless of the weights each residual will get). While if the model is biased, but the weighting model is well specified, then the bias will be well estimated (And corrected for) by the weighted average residuals

The bias of the doubly robust estimators is called a second-order bias, and it depends on the product of the difference 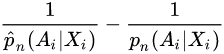 and the difference . This property allows us, when having a "large enough" sample size, to lower the overall bias of doubly robust estimators by using machine learning estimators (instead of parametric models).

【翻译】

后来公式的重新排列有助于揭示潜在的想法: 我们的估计是基于使用模型(即: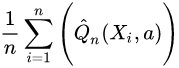)的平均预测结果。然而，如果模型是有偏差的，那么模型的残差将不会(在完整的治疗组 a)在0左右。我们可以通过从结果(Y)的真实值(即: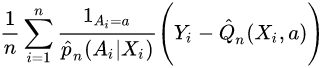)中加入模型(Q)的平均残差的额外项来纠正这种潜在的偏差。因为我们缺少 Y 的值，所以我们给出权重来夸大每个残差的相对重要性(这些权重是基于看到每个受试者观察结果的逆倾向，也就是概率)(参见第10页)。

这种估计器的“双重稳健”好处来自于这样一个事实，即它足以正确指定两个模型中的一个，使估计器是无偏的(或者，或者两者兼而有之)。这是因为如果结果模型被很好地指定，那么它的残差将在0左右(不管每个残差将得到的权重如何)。如果模型是有偏差的，但加权模型是明确规定的，那么偏差将由加权平均数残差得到很好的估计(和校正)

双稳健估计量的偏差称为二阶偏差，它取决于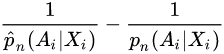差和差的乘积。这个性质允许我们，当有一个“足够大”的样本量，以降低整体偏差的双鲁棒估计使用机器学习估计(而不是参数模型)。

编辑推荐

文章推荐

缺失数据和因果推断中的双稳健方法介绍 | 周日直播·因果科学读书会 | 集智俱乐部 (swarma.org)

课程推荐

缺失数据和因果推断中的双稳健方法介绍 | 因果科学第三季第十八期 - 因果科学与Causal AI读书会第三季

这个视频内容来自集智俱乐部读书会因果科学读书会第三季内容的分享，主题是”缺失数据和因果推断中的双稳健方法介绍“，北京大学北京国际数学研究中心博士后吴鹏分享。本次报告对双稳健方法的基本原理和思路做一个概要介绍，内容包括经典双稳健方法及其局限性。为克服双稳健性的局限性，进一步介绍双稳健回归估计，双稳健逆概率加权估计，偏差下降的双稳健估计。最后，我们总结双稳健方法的一般框架：双稳健估计方程，双稳健损失函数。前者可用于得到一般模型参数的双稳健估计，后者常用于预测问题中。

相关路径

• 因果科学与Casual AI读书会必读参考文献列表，这个是根据读书会中解读的论文，做的一个分类和筛选，方便大家梳理整个框架和内容。
• 因果推断方法概述,这个路径对因果在哲学方面的探讨，以及因果在机器学习方面应用的分析。
• 因果科学和 Causal AI入门路径，这条路径解释了因果科学是什么以及它的发展脉络。此路径将分为三个部分进行展开，第一部分是因果科学的基本定义及其哲学基础，第二部分是统计领域中的因果推断，第三个部分是机器学习中的因果（Causal AI）。
• 复杂网络动力学系统重构文献，这个路径是张江老师梳理了网络动力学重构问题，描述了动力学建模的常用方法和模型，并介绍了一些经典且重要的论文，这也是复杂系统自动建模读书会的主要论文来源，所以大部分都有解读视频。
• 因果纠缠集智年会——因果推荐系统分论坛关于因果推荐系统的参考文献和主要嘉宾介绍，来源是集智俱乐部的因果纠缠年会。