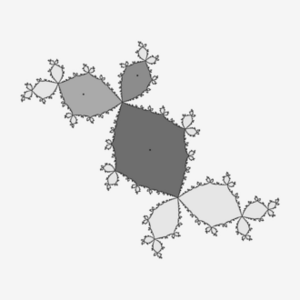
吸引子
在动力系统的数学领域中,吸引子 attractor是系统在众多初始条件下所趋向的一组数值。即使稍微受到干扰,与吸引子的值接近的系统值仍然能够保证近似性。
在有限维系统 finite-dimensional systems中,演化变量可用代数表示为 n 维向量。吸引子是n维空间中的一个区域。在物理系统中,n维可以是一个或多个物理实体的两个或三个位置坐标;在经济系统中,它们可以是单独的变量,如通货膨胀率 inflation rate和失业率 unemployment rate。
如果演化变量是二维或三维的,则动态过程的吸引子可以用几何方式表示为二维或三维(例如右图所示的三维情况)。一个吸引子可以是一个点,一个有限的点集,一条曲线,一个流形,甚至是一个具有分形结构的复杂集合——我们称之为奇异吸引子 strange attractor(见下面的奇异吸引子)。如果变量是标量,那么吸引子就是实轴的子集。描述混沌动力学系统 chaotic dynamical systems的吸引子是混沌理论的重要成果之一。
动力系统在吸引子中的轨迹,若时间向前,不必满足任何特殊的约束条件。轨迹可能是周期性的,也可能是混沌的。如果一组点是周期性的或混沌的,但其附近的流远离该集合,则该集合不是吸引子,而是排斥点(或斥点) repeller(or repellor)
吸引子的提出动机
我们通常用一个或多个微分方程或差分方程描述动力系统。一个给定动力系统的方程可以表明它在任何给定短时间内的行为。为了确定系统在较长时间内的行为,我们往往需要通过分析手段或迭代 Iteration(通常借助于计算机)来对方程进行积分。
物理世界中的动力系统往往产生于耗散系统 dissipative system:如果没有某种驱动力,运动就会停止。(耗散可能来自内部摩擦,热力学损失,材料损失等许多原因。)当耗散和驱动力趋于平衡时,初始瞬态 Initial transients会被消除,使系统进入其典型状态。与典型状态相对应的动力系统相空间的子集是吸引子——也称为吸引部分。
不变集 Invariant sets和极限集 limit sets的概念与吸引子类似。不变集是在动力学作用下向自身演化的集合。[1]不变集可能包含于吸引子。极限集是一组点,这些点存在一定的初始状态,但是随着最终时间趋近无穷远时将任意接近极限集(即收敛到集合的每个点)。吸引子是极限集,但不是所有的极限集都是吸引子: 系统的某些点可能会收敛到极限集,但是稍微偏离极限集的点可能会被敲掉,永远不会回到极限集附近。
例如,阻尼摆 damped pendulum有两个不变点: 最小高度点x0和最大高度点x1。点x0也是一个极限集,因为轨迹向它收敛;点 x1不是一个极限集。由于空气阻力的耗散,点x0也是吸引子。如果没有耗散,x0就不会出现吸引子。亚里士多德 Aristotle认为物体只有在被推动时才会移动——这是耗散吸引子 dissipative attractor的早期表述。
有些吸引子是混沌的(参见奇异吸引子),在这种情况下,吸引子的任意两个不同点的演化都会触发指数发散轨迹。此时即使系统中有一点噪声,预测也会因此而变得复杂。[2]
数学定义
设t表示时间,设f(t,•)为指定系统动力学的函数。也就是说,如果a是n维相空间中一个表示系统初始状态的点,那么f(0,a)=a。对于t的正值,f(t,a)是该状态在t个时间单位之后演化的结果。例如,如果系统描述了自由粒子在一维空间中的演化,那么相空间是坐标为(x,v)的平面 R2 ,其中x是粒子的位置,v是粒子的速度,a = (x,v),由以下给出
- [math]\displaystyle{ f(t,(x,v))=(x+tv,v).\ }[/math]
吸引子是相空间 phase space的子集 subset A——这需要具有以下三个条件:
- “A”是“f”中的“前向不变”:如果“a”是“A”的元素,则对于所有“t”>0,“f”(“t”,“a”)也是。
- 存在一个“A”的邻域称为“A”的“吸引域”,表示为“B”(“A”),它由所有“B”点组成,这些点“B”在极限t → ∞"时“进入”A“。更正式地说,“B”(“A”)是相空间中所有点“B”的集合,具有以下特性:
- 对于“A”的任何开邻域“N”,存在一个正常数“T”,使得对所有实数“t”>“T”,有f(t,b)∈N,。
- “A”中不存在具有前两个属性的真(非空)子集。
由于吸引域包含一个含有“A”的开集合,所以每一个足够接近“A”的点都会被“A”吸引。吸引子的定义使用了相空间上的一个度量,但得到的结果通常只取决于相空间的拓扑结构。在Rn的情况下,我们通常会使用欧氏范数 Euclidean norm。
在文献中有吸引子的其他定义出现。例如,一些作者要求吸引子具有正测度(防止一个点成为吸引子),另一些作者则弱化了B(A)作为一个邻域的要求。[3]
吸引子的类型
吸引子是动力系统的相空间的一部分或子集。直到20世纪60年代,吸引子被认为是相空间的简单几何子集——像点、线、面和简单的三维空间。更复杂的吸引子,不能被归类为简单的几何子集,如拓扑野生集 topologically wild sets——虽然在当时是已知的,但却被认为是精巧的异常事物。斯蒂芬·斯梅尔 Stephen Smale能够证明他的马蹄映射是稳定的,它的吸引子具有康托尔集 Cantor set结构。
不动点 fixed point和极限环 limit cycle是两类简单的吸引子。吸引子可以呈现出许多几何形状(相空间子集)。但当这些集合(或其中的运动)不能简单地描述为基本几何对象(例如,直线,曲面,球体,环面,流形)的简单组合(例如,交集和并集)时,这个吸引子就被称为“奇异吸引子”。
驻点
函数或变换的不动点是能够通过函数或变换映射到自身的点。如果我们把动力系统的演化看作是一系列的转变,那么在每一转变中,都可能会有一个点是固定的——当然也可能没有。动力系统的最终状态与该系统演化函数的吸引固定点相对应,例如阻尼摆的中心底部位置,玻璃杯中晃动水的水平线和平坦线,在碗的底部中心滚动的大理石。但是动态系统的不动点不一定是系统的吸引子。例如,如果装有滚动大理石的碗被倒置,大理石在碗的顶部达到平衡状态,碗的中心底部(现在是顶部)就是一个固定的状态但不是一个吸引子。这等价于稳定平衡点和不稳定平衡点之差。如果一个大理石在一个倒碗(山)的顶部,这个在碗(山)的顶部的点是一个固定点(平衡),但不是一个吸引子(稳定的平衡)。
此外,由于物理世界动力学的现实性——包括非线性动力学的粘滞,摩擦,表面粗糙度,变形(弹性和塑性),甚至量子力学 quantum mechanics——至少拥有一个固定点的物理动力系统总是有多个固定点和吸引子。[4]回到倒置碗顶上的大理石这一例子,即使碗看起来是完美的半球形,大理石是规范的球形,在显微镜下观察时它们的表面实际上都十分复杂,它们的形状在接触过程中改变。任何物理表面都可以被视作一个由多个山峰、山谷、鞍点、山脊、峡谷和平原组成的崎岖地形。[5]在这个表面地形中有许多点(以及在这个微观地形上滚动的同样粗糙的大理石的动力系统)被认为是静止的或不动的,其中一些被归类为吸引子。
有限点数
在一个离散时间系统中,吸引子可以以有限数量点的形式出现——这些数量点可以被依次访问。其中每个点都被称为周期点。逻辑图说明了这一点,根据其特定参数值,对于任何“n”值,可以有由2n点、3×2n点等组成的吸引子。
极限环
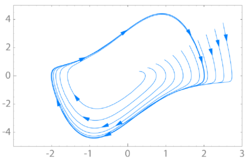
极限环是连续动力系统的周期轨道,它是孤立点。例如时钟的摆动,以及休息时的心跳。(理想摆的极限环不是极限环吸引子的一个例子,因为它的轨道不是孤立的:在理想摆的相空间中,在一个周期轨道的任何一个点附近都有另一个点属于不同的周期轨道,因此前一个轨道不具有吸引力)。
极限环
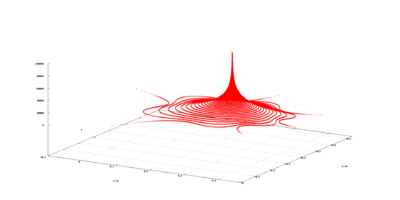
在处于极限循环状态的系统的周期轨迹中可能存在多个频率。例如,在物理学中,一个频率可以决定一颗行星围绕恒星运行的速率,而第二个频率则描述了两个天体之间的距离振荡。如果其中两个频率形成无理分数 irrational fraction(即它们是非公度),则轨迹不再闭合,极限循环变成极限环。如果存在Nt非公度频率,这种吸引子被称为Nt环面。例如这个2环面体:
与这个吸引子对应的时间序列是一个准周期序列: 具有非公度频率的周期函数(不一定是正弦波)的离散采样和。这样的时间序列不具有严格的周期性,但其功率谱仍然只包含锐线。
奇异吸引子
如果吸引子具有分形结构,则称为“奇异”。这种情况通常发生在在当它的动力学系统符合混沌理论时,但是奇异的非混沌吸引子也存在。如果一个奇异吸引子是混沌的,表现出对初始条件的敏感依赖性,那么在吸引子上两个任意接近的备选初始点经过多次迭代后,都会指向任意相距很远的点(受吸引子的限制),而在经历其他次数的迭代之后,会指向任意接近的点。因此,具有混沌吸引子的动态系统是局部不稳定但全局稳定的:一旦一些序列进入吸引子,附近的点就会发散,但不会离开。[6]
术语“奇异吸引子”由David Ruelle和Floris Takens提出,用来描述吸引子——产生于刻画流体的系统的一系列分叉。[7]奇异吸引子通常在几个方向上可微,但有些吸引子与康托尘类似,因此不可微。在噪声条件下,人们也能发现奇异吸引子,这可以用来支持Sinai-Ruelle-Bowen型的不变随机概率测度。[8]
动力学方程的参数随着方程的迭代而变化,具体值可能取决于初始参数。其中一个例子是得到深入研究的逻辑图, [math]\displaystyle{ x_{n+1}=rx_n(1-x_n) }[/math],图中显示了参数r各种值的吸引域。如果[math]\displaystyle{ r=2.6 }[/math],则[math]\displaystyle{ x\lt 0 }[/math]的所有起始x值将迅速使函数值变为负无穷大;[math]\displaystyle{ x\gt 0 }[/math]的起始x值将变为正无穷大。但是对于[math]\displaystyle{ 0\lt x\lt 1 }[/math],x值会迅速收敛到[math]\displaystyle{ x\approx0.615 }[/math],也就是说,在这个r值下,x的单个值是函数行为的吸引子。对于r的其他值,x可以取多个值:如果r为3.2,[math]\displaystyle{ 0\lt x\lt 1 }[/math]的起始值将导致函数值在[math]\displaystyle{ x\approx0.513 }[/math]和[math]\displaystyle{ x\approx0.799 }[/math]之间交替。在r的某些值处,吸引子是一个单点(“不动点”),在r的其他值处,依次访问x的两个值(倍周期分岔);在r的其他值处,依次访问任意数量的x值;最后,对于r的某些值,访问无穷多个点。因此,同一个动力学方程可以有不同类型的吸引子,这取决于它的起始参数。
奇异吸引子的例子包括双涡卷吸引子 double-scroll attractor、埃农吸引子 Hénon attractor、若斯叻吸引子 Rössler attractor和洛伦兹吸引子 Lorenz attractor。
吸引子表征系统的演化
吸引子的吸引域是相空间的区域,迭代在这个区域上得到定义,使得该区域中的任何点(任何初始条件)都将渐近地迭代到吸引子中。对于一个稳定的线性系统,相空间中的每一点都在吸引域中。然而,在非线性系统中,有些点可能直接或渐近地映射到无穷大,而另一些点可能位于不同的吸引域中并渐近映射到不同的吸引子;其他初始条件则可能位于或直接映射到非吸引点或循环中。
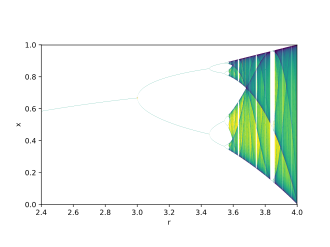
动力学方程的参数随着方程的迭代而变化,具体值可能取决于初始参数。一个例子是得到深入研究的逻辑图,[math]\displaystyle{ x_{n+1}=rx_n(1-x_n) }[/math],图中显示了参数r各种值的吸引域。如果[math]\displaystyle{ r=2.6 }[/math],则[math]\displaystyle{ x\lt 0 }[/math]的所有x值将迅速使函数值变为负无穷大;[math]\displaystyle{ x\gt 0 }[/math]的起始x值将变为正无穷大。但是对于[math]\displaystyle{ 0\lt x\lt 1 }[/math],x值会迅速收敛到[math]\displaystyle{ x\approx0.615 }[/math],也就是说,在这个r值下,x的单个值是函数行为的吸引子。对于r的其他值,x可以取多个值:如果r为3.2,[math]\displaystyle{ 0\lt x\lt 1 }[/math]的起始值将导致函数值在[math]\displaystyle{ x\approx0.513 }[/math]和[math]\displaystyle{ x\approx0.799 }[/math]之间交替。在r的某些值处,吸引子是一个单点(“不动点”),在r的其他值处,依次访问x的两个值(倍周期分岔);在r的其他值处,依次访问任意数量的x值;最后,对于r的某些值,访问无穷多个点。因此,同一个动力学方程可以有不同类型的吸引子,这取决于它的起始参数。
齐次形式的单变量(单变量)线性差分方程[math]\displaystyle{ x_t=ax{t-1} }[/math]从除0以外的所有初始点|a|>1发散到无穷大;没有吸引子,因此没有吸引池。但是如果|a|<1,则数线图上的所有点渐进地(或在0的情况下直接)趋向0;0是吸引子,整个数线是吸引域。
吸引池
同样地,动态向量X中的线性矩阵差分方程,如果a的最大特征值绝对值大于1,则动态向量X中的所有元素[math]\displaystyle{ X_t=AX_{t-1} }[/math] 都将发散到无穷大;不存在吸引子和吸引池。但如果最大特征值小于1,则所有初始向量将渐近收敛于零向量,即零为吸引子;潜在初始向量的整个n维空间就是吸引池 basin of attraction。
吸引子的吸引域是相空间的区域,迭代在这个区域上得到定义,使得该区域中的任何点(任何初始条件)都将渐近地迭代到吸引子中。对于一个稳定的线性系统,相空间中的每一点都在吸引域中。然而,在非线性系统中,有些点可能直接或渐近地映射到无穷大,而另一些点可能位于不同的吸引域中并渐近映射到不同的吸引子;其他初始条件则可能位于或直接映射到非吸引点或循环中。[9]
类似的特征也适用于线性微分方程。标量方程[math]\displaystyle{ dx/dt =ax }[/math] 使得除0以外的所有 x 的初始值在 a > 0时发散到无穷大,但在 a < 0时收敛到吸引子,使整条数轴成为0的吸引域。如果矩阵A的其中一个特征值是正的,则该矩阵系统[math]\displaystyle{ dX/dt=AX }[/math]从除零向量以外的所有初始点发散; 但如果所有特征值都是负的,则零向量就是吸引域,它是整个相空间的吸引子。
线性方程或系统
如果除了0以外的所有初始点|“A”>>1,单变量线性齐次方程[math]\displaystyle{ x_t=ax_{t-1} }[/math](差分方程)发散到无穷大;没有吸引子,因此没有吸引域。但如果 |a| < 1,则数轴上的所有点渐进(或在0的情况下直接映射)到0;0是吸引子,整个数轴都是吸引域。
与线性系统相比,非线性方程或系统有更多样的行为。一个例子是非线性表达式根的牛顿迭代法。如果表达式有多个实根,则迭代算法的某些起始点会渐近地靠近其中一个根,而其他起始点会得出另一个根。表达式根的吸引域通常并不简单,最接近某一个根的点都被映射到那里,从而形成由附近点组成的吸引区。吸引域在数量上可以是无限的,大小上可以任意小。例如,对于函数[math]\displaystyle{ f(x)=x^3-2x^2-11x+12 }[/math],在连续的吸引域中以下初始条件:
同样的,针对在动态向量X中的线性矩阵差分方程(在平方矩阵a'中表现为齐次形式[math]\displaystyle{ X_t=AX_{t-1} }[/math]),如果A的最大特征值在绝对值上大于1,则动态向量的所有元素将发散到无穷大;没有吸引子,也没有吸引池。但如果最大特征值小于1,则所有初始向量将渐近收敛于零向量,即零为吸引子;潜在初始向量的整个n维空间就是吸引池。
用牛顿法求解 x5 − 1 = 0。相似颜色区域中的点映射到同一个根; 颜色较深意味着需要更多的迭代来收敛。
类似的特征也适用于线性微分方程。标量方程[math]\displaystyle{ dx/dt=ax }[/math]会导致x的所有初始值(除了0)发散到无穷大,如果“a”<0,则收敛到值为0的吸引子,使整条数线成为0的吸引域。如果矩阵A的任何特征值都为正,则矩阵系统的[math]\displaystyle{ dX/dt=AX }[/math]会从除零向量外所有的初始点发散;但如果所有特征值都为负,则零点向量是一个吸引子,其吸引域是整个相空间。
非线性方程或系统
与线性系统相比,非线性方程或系统可以产生更多行为。一个例子是非线性表达式根的牛顿迭代法。如果表达式有多个实根,则迭代算法的某些起始点会渐近地靠近其中一个根,而其他起始点会得出另一个根。表达式根的吸引池通常并不简单,最接近某一个根的点都被映射到那里,从而形成由附近点组成的吸引区。吸引池在数值上可以是无限的,可以任意小。例如[10]对于函数[math]\displaystyle{ f(x)=x^3-2x^2-11x+12 }[/math],以下初始条件在连续的吸引池中
2.35287527收敛到4;
2.35284172 收敛到 -3;
2.35283735收敛到4;
2.352836327 收敛到 -3;
2.352836323 收敛到 1。
牛顿法也可以应用于求复变函数的根。在复杂的平面上,每个根部都有一个吸引池; 这些区域可以如图所示绘制出来。可以看出,为一个特定的根而组合成的吸引池可以有许多不相连的地区。对于许多复杂函数来说,吸引池的边界为分形。
对于具有周期边界条件的三维不可压缩方程 Navier-Stokes equation,如果它有一个全局吸引子那么这个吸引子将是有限维的。
牛顿方法也可以应用于复杂分析以找到它们的根。每个根在复合平面中都有一个吸引盆;如图所示,可以绘制这些盆地的地图。可以看出,特定根的组合吸引盆地可以有许多断开的区域。对于许多复杂函数,吸引盆地的边界为分形。
偏微分方程
抛物型偏微分方程可能具有有限维吸引子。在某些情况下,方程的扩散部分会阻抑更高的频率,触发一个全局吸引子。金兹堡-朗道方程 Ginzburg-Landau equations 、 K-S方程 Kuramoto-Sivashinsky equations和二维强迫纳维-斯托克斯方程 forced Navier–Stokes equation都具有有限维的全局吸引子。
对于具有周期性边界条件的三维不可压缩 Navier-Stokes 方程,如果它具有全局吸引子,则该吸引子将是有限维的。[11]
另见
参考文献
- ↑ Carvalho, A.; Langa, J.A.; Robinson, J. (2012). Attractors for infinite-dimensional non-autonomous dynamical systems. 182. Springer.
- ↑ Kantz, H.; Schreiber, T. (2004). Nonlinear time series analysis. Cambridge university press.
- ↑ John Milnor (1985). "On the concept of attractor". Communications in Mathematical Physics. 99 (2): 177–195. doi:10.1007/BF01212280.
- ↑ Greenwood, J. A.; J. B. P. Williamson (6 December 1966). "Contact of Nominally Flat Surfaces". Proceedings of the Royal Society. 295 (1442): 300–319. doi:10.1098/rspa.1966.0242.
- ↑ Vorberger, T. V. (1990). Surface Finish Metrology Tutorial. U.S. Department of Commerce, National Institute of Standards (NIST). p. 5. https://www.nist.gov/calibrations/upload/89-4088.pdf.
- ↑ Grebogi Celso, Ott Edward, Yorke James A (1987). "Chaos, Strange Attractors, and Fractal Basin Boundaries in Nonlinear Dynamics". Science. 238 (4827): 632–638. doi:10.1126/science.238.4827.632.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ Ruelle, David; Takens, Floris (1971). "On the nature of turbulence". Communications in Mathematical Physics. 20 (3): 167–192. doi:10.1007/bf01646553.
- ↑ Chekroun M. D.; Simonnet E.; Ghil M. (2011). "Stochastic climate dynamics: Random attractors and time-dependent invariant measures". Physica D. 240 (21): 1685–1700. CiteSeerX 10.1.1.156.5891. doi:10.1016/j.physd.2011.06.005.
- ↑ Strelioff, C.; Hübler, A. (2006). "Medium-Term Prediction of Chaos". Phys. Rev. Lett. 96 (4): 044101. doi:10.1103/PhysRevLett.96.044101. PMID 16486826.
- ↑ Dence, Thomas, "Cubics, chaos and Newton's method", Mathematical Gazette 81, November 1997, 403–408.
- ↑ Geneviève Raugel, Global Attractors in Partial Differential Equations, Handbook of Dynamical Systems, Elsevier, 2002, pp. 885–982.
编者推荐
集智课程
圣塔菲课程:Introduction to Dynamical Systems and Chaos
本课程主要介绍动力学系统和混沌系统,您将学到蝴蝶效应(butterfly effect)、奇异吸引子(attractors)等基本概念,以及如何应用于您感兴趣的领域。课程主题涉及相空间(phase space),分叉(bifurcations),混沌(chaos),蝴蝶效应(butterfly effect),奇怪吸引子(strange attractors)和模式生成(pattern formation)。
相空间重构方法 | 复杂系统自动建模读书会第6期
该课程内容是围绕论文《Geometry from a Time Series Predicting chaotic time series》进行的分享。关于相空间重构,即利用时间序列数据重构吸引子,通常都是使用Taken定理,来直接构成原始的相空间中的轨迹。
其他
本中文词条由水流心不竞初译,由和光同尘审校,Lunji、薄荷编辑,如有问题,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。