基于流网络的社区发展预测
研究背景
社团研究一直是社会科学研究重要的一个领域,而其中一个社团如何形成以及如何随时间演化又是当中最主要的方向之一。找到一系列指标能够刻画和识别社团中的潜力股,判断一个社团会不会不断成长,是否能够长期存活,对整个互联网领域以及社会科学具有重大的实际意义。因此,众多的科学家投入了大量的精力来分析社团发展问题,并建立了一系列的模型。但是传统的研究大多集中只针对特定的网络,尤其是那些已经取得巨大成功的社区网站,比如facebook, twitter,flicker之类,很少有人关注那些存活时间短的社区[],此外,人们常常通过对微观个体对行为来模拟整个社区的发展,很少从一个大尺度的范围内来刻画整个社区的发展。最近,Sanjay Kairam等人通过对整个社区网络结构的角度出发,希望能够预测一个社区的生长和生存周期,并且取得了很好的效果。
我们认为,社区网络的结构确实在社区的发展中起到了一定的作用,但追本溯源,一个社区之所以能够不断发展,靠的就是不断的吸引用户访问点击,而整个网络的结构也是由于用户行为模式的冲刷从无到有的形成过程,所以要预测一个社区能否生存且是否可以不断的快速增长,了解这个社区中的用户行为是最本质的解决途径。
大量用户在社区中的点击数据,为我们的这一研究给予了可能性和方便,为了能够研究不同社区的用户模式,以及消除除此之外的其它影响因素,我们选择了stackexchange,因为这是一个一系列问答网社区的平台,旗下的网站总共有133个,覆盖了各种不同领域的问答话题。我们希望能够通过用户在这些不同社区中的不同行为模式,找到能够刻画和衡量一个社区好坏的指标,并以此来对社区的增长进行预测分析。
研究方法
数据来源
研究使用的数据,全部来自Stack Exchange,它是一系列问答网社区的集成平台,旗下的网站总共有133个,覆盖了包括数学、物理、经济、 烹饪等不同领域的问答话题,其中最耳熟能详的就是Stack Overflow网站了。我们从它公开开放的数据集中下载了截至到2014年1月的数据(下载地址:https:// archive.org/details/stackexchange.)。这些数据都是Exchange从基于用户输入内容的一个自由访问、匿名存储的堆栈中得到的,符合全部的许可要求。我们下载的数据集包含了所有133个社区的日志文件。其中,最小的社区为itanlian.stackexchange.com社区,建立于2013年10月,包含了374个用户,194个问题和387个回答。最大的社区为stackoverflow,它建立于2008年6月,包含了2728224个用户,6474687个问题和11540788个回答。
在对用户的回答和提问活动进行分析之前,我们对数据进行了初步整合,每个构成我们网络的用户成员都有一个独立的日志文件,包含用户的位置文件,这样可以确保对用户生成的活动进行各种反垃圾邮件机制,确保数据的可用性和有效性。
注意力流网络
从原始的数据中,我们可以从中抽取一部分的有效数据,包括用户活动的时间,活动的类型(回答或者提问),这样,我们就有了一系列提问和回答的事件序列。我们可以从中总体的分析一个社区的提问和回答情况。
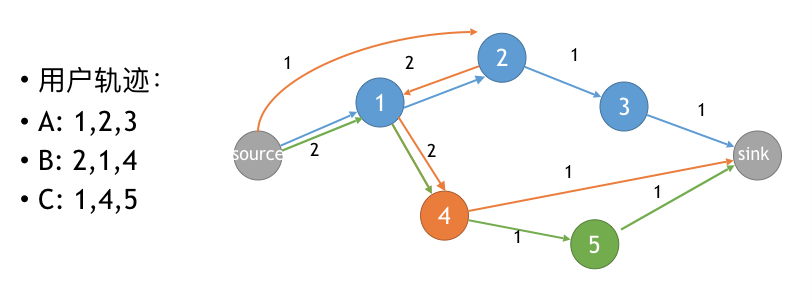
那么,进一步我们如何对每个社区构建一个注意力流网络呢?关于这个问题,我们可以根据用户的回答问题先后来构建。用户回答的先后可以粗略的看作是用户在这个论坛上的注意力转移的轨迹,在我们得到的数据中,每一个回答的记录都有一个用户编号,回答的日期,回答时间,回答的问题编号。由此,我们可以按照日期顺序,构建每个用户的回答问题序列。通过整个所有用户的回答序列,我们就能够得到整个社区的注意力流网络,其中网络中的节点表示为社区中的每个问题,权重为从i到j的人数流量。如果一个用户回答完i问题后回答j问题,那么就建立一条从i到j的连边,且该边流量为1.如果i和j的连边已经存在,那么,该边的权重将增加1.整个构建的过程可以用下图表示:
流距离
流距离是开放流网络中一个重要的指标,它是定义了网络中两个节点之间的平均首达距离(具体可以参见流网络词条)。其实,在一个社区中,对于一个用户而言,他总是从源进入,并最终流向汇节点。但是,这其中的路径可以各不相同,有些曲曲折折,有些单刀直入,图2形象的反应了用户不同的行为路径。
那么,用户的这些游走轨迹,会不会影响整个网络社区的发展呢?这就是我们想要研究的问题。 在这里,我们定义了两个流距离,一个是节点到源的流距离,它表示用户之前到行为,该问题用户进入问答社区后多久才能到达。另一个是节点到汇流距离,它表示用户之后的行为,在到达后经过多少步才下线。因此,对于每一个节点(问题)都有一个2元组(到源距离,到汇距离),我们可以通过这个,将整个流网络映射到一个新的2维空间,如下图3所示:
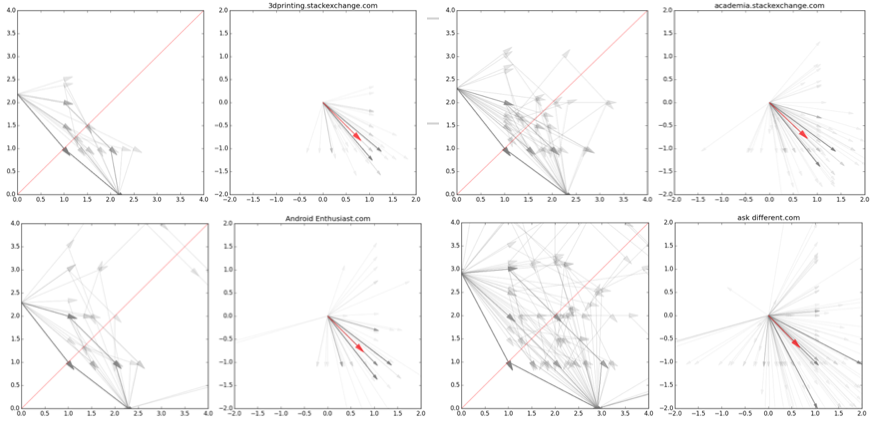
横轴表示到汇的距离,纵轴表示到源的距离,每个坐标点,可以代表一个问题,用户的每一步跳转,都可以表示成这个空间中坐标的变换,箭头表示变化的方向。因此,这个空间中所有的用户的跳转变化,都能在这个空间中表示出来。我们随机选取了4个社区,绘制处理用户的空间跳转变化图。如下图4左子图所示。
这些用户或有意或无意的游走,使得跳转的变化图有点复杂,难以看清,虽然已经能看到有些社区跳转的变化幅度不大,而有些跳转的区域变化特别大。为了更好的显示出,用户在社区中跳转行为的差异性和范围大小,我们将空间中这些箭头矢量都合并到原点,如图4右子图所示。我们可以清楚的看到,对于不同问答社区,这些从原点出发的矢量辐射范围不一样,有些分散,覆盖范围大,而有些矢量集中,覆盖范围小。因此,我们认为所有用户的行为,用从原点开始的这些矢量的分散程度来衡量。
社区发展指标
我们假设,对于一个社区,其角度越分散,则说明用户越具有创造性和活跃性,那么对该社区的长期发展也越有利。为了验证这个观点,我们引入了信息熵的概念,来描述整个流网络角度分布的复杂(分散)程度,并将其定义为系统的角度熵。
(角度熵的公式)
角度熵越大,则说明用户行为越发散,创造性越强,相反,角度熵越小,则说明用户同质性较高,行为跳转幅度不大。 为了验证我们的假设,我们选取了各个社区发展一半的时候,作为我们的观测点,用来计算不同社区的角度熵,用了截止月的问题数和回答数增长率作为最终社区的发展情况,通过两者的皮尔逊相关系数,来验证两者存在相关性,即角度熵越大,社区的发展越好。
结果分析
社区总体发展
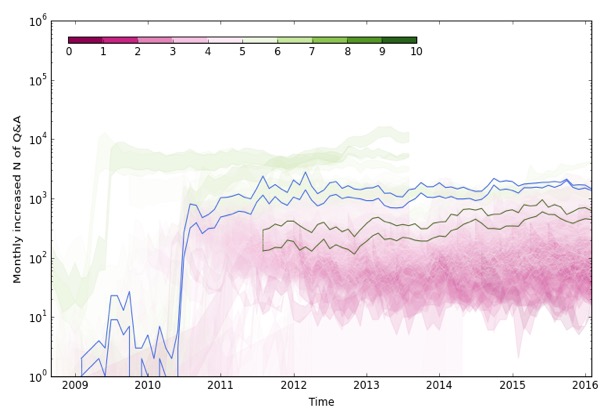
我们首先对这100多个社区的发展情况,做了总体的统计性描述,分别计算了每个社区每一天的提问数和回答数,并绘制了其随时间的累积增长曲线。如下图所示:
每条带子是一个社区,上界是每月新增答案数,下界是每月新增问题数。一共有154个社区。颜色代表社区的问答总数(取对数再减去5)。我们还可以选择性地标示出某些社区,例如本图中标示出了apple类(蓝色)和旅游类(深绿色)两个社区。从图中我们可以看到,各个社区的问答总数分布区间范围差异比较大,大部分社区每月增加量比较少,只有少数几个巨大的大型社团,每月的增长量巨大。此外,我们也发现,对于大多数社区,在发展的前期存在巨大的增幅波动,都有一个快速发展的时期,其后社区的问答增幅趋紧平衡,已相对稳定的增加量发展。值得探讨的是,对于那些快速发展,且问答数巨大的社团而言,除了早期的迅猛增加外,其到稳定增幅到时间间隔更为短暂,且总体来说,问题的回答数都要高于提问数,而对那些增量小的社团而言,他们的发展似乎前期处于一种跳跃波动阶段,增幅极不稳定,且回答数的增加常常小于提问数,且这类社区最后随时间有增加量缓慢减小的趋势。
社区发展与角度熵的相关性
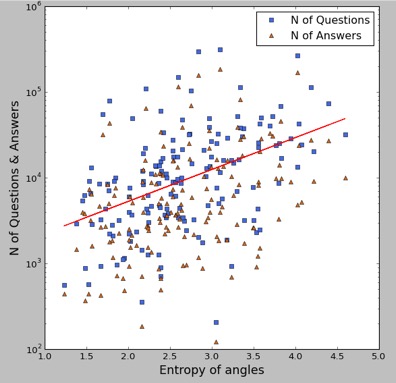
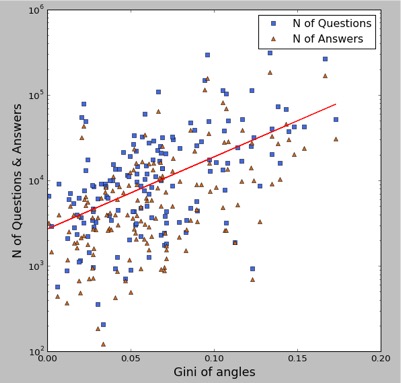
为了直观的观察社区发展与角度熵的相关关系,我们对其进行了回归分析,如下图左所示,其中横轴是各个社区的角度熵,纵轴是个社区截止时间的问题数和回答数,红线是回归线。从中我们可以看到,对于一般社区而言,用户的游走的角度熵越大,说明用户越有创造性和发散性,对于问答社区的长期发展也越有利。
由于角度熵在划分的时候,对于bin区间的选取具有随机性和较强的依赖性,我们进一步计算了每个社区角度的基尼系数,如右子图所示,我们发现这种行为模式更加的明显。对于一个社区而言,如果用户游走的越分散,则社区的未来发展也会相对越好!
个参数对预测的影响
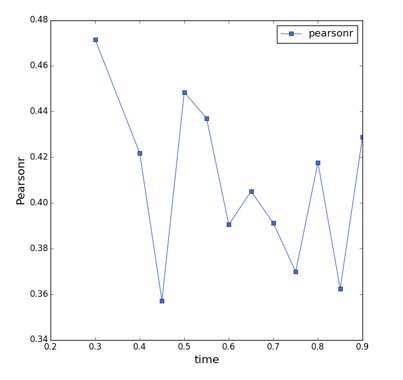
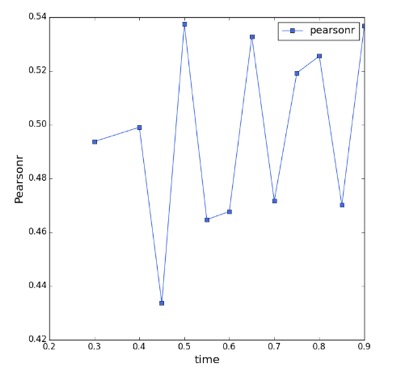
在我们模型中,是通过计算社团发展一半时的各项指数来预测社团能否成长。可见时间参数是一个不可忽视的因素,可能对我们的结果造成影响。因此我们进一步查看了时间参数对结果的影响。我们通过计算不同社区不同时段的发展角度熵以及基尼系数与最终社团的发展规模来判断截取的时间参数是否影响。
上图分别是角度熵和基尼系数与最终社区规模的皮尔逊相关系数随预测截取时间的变化图。从图中,我们可以清楚的发现,无论在社团发展到合适对其之后的规模进行预测,相关性虽然有所波动,但是并不剧烈,其均值都基本围绕在0.41和0.50左右。
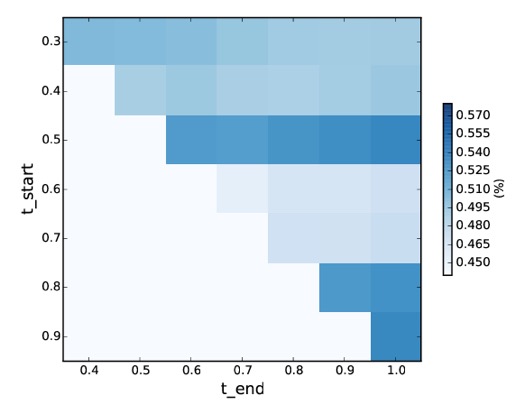
尽管如此,我们仍然有疑问。因为对于一个仍在发展的社团而言,它最终规模的时间我们无法知道又如何能够预测呢?为了更好的解决这个问题,我们又进一步的通过一张热度图来反映整个模型的鲁棒性。
上图是不同时段的截取点与不同时段的预测点的基尼相关性热度图。其中,纵轴代表不同的截取时间点,横轴代表要预测的时间(例0.3表示社团发展到30%左右的时候作为预测点,截取点同理),颜色越深,说明相关性越强。
讨论
虽然最后得到的结果比较好,但是仍然存在着值得推敲的事情。其中最主要的有几点。首先是没有对比的null model,在整个模型中,我们发现确实一个社区用户游走的角度熵或者基尼系数越大而言,他最终预测点的发展也越好,可是同理,越大的社区其本身就能让用户的游走更加的具有较深较广的范围,所以两者之间的相关性需要一样对照模型来检验。应该进一步比较在截断时间点两个发展规模相同的网络社区,他们的角度熵以及基尼系数与最终社团规模的相关性。同时,null model的加入,可以让我们明白,在除去社团大小的影响下,真的这个指标能够反映是人的行为导致了一个社团能否长期的发展。另外一个,研究中为了方便,我们选取了前100个用户,但这个选取的人数缺少理论依据,更准确的应该是所有用户的游走,有待更深入的计算。其次,我们现在选取的截取点是依据社团自身发展时间而言,能否让这个取值固定,即都使用一个月的时间来进行预测,消除其他因素的影响,其结果是否成立有待我们在以后进行检验。