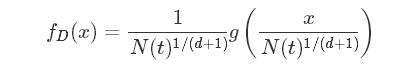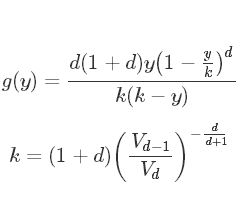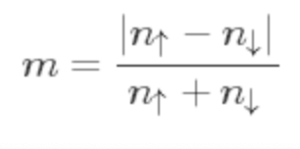复杂网络下的伊辛模型
本文由章彦博同学进行撰写,井静宜同学进行编辑。
本文将复杂网络与Ising模型结合,使用随机几何图模型,构造复杂网络,并在网络的基础上运行Ising模型。探索了其临界温度,发现临界温度与粒子数具有密切关联。同时发现相邻的集团之间,具有较强的独立性,并做了具体的数值分析。临界温度与独立性包涵了重要的现实意义,对于物质生长、凝聚具有解释效力;对于很多社会问题,也可以基于此模型给出解释 。
引言
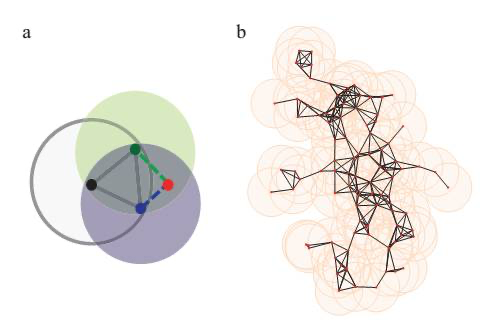
事物之间的关联,可以简单地使用网络来表示。网络中的节点,可以表示模型中的个体;而连边则表示其之间的关系。事实证明,大量事物可以用网络表示。但真实世界的网络的结构,与我们常见的渔网般规整的结构不同,也与简单计算机程序随机生成的网络不同。它们大多兼具大的簇系数和小的平均距离1。例如电力网络、社会关系网络、交通网络,皆有此特征23。而相关的学科,例如计算社会学等,则依托此类结构,进行学术研究。近年则发展出一些方法,对网络的拓扑重新构造,从而简化了网络结构,此称为“流形学习”4。复杂网络有多种类型,根据生成其的模型不同而不同,常见的有小世界网络。而此文使用的是一种类似优先连接构成的网络,称为“随机几何图”5。其基本构造方法如下图所示:
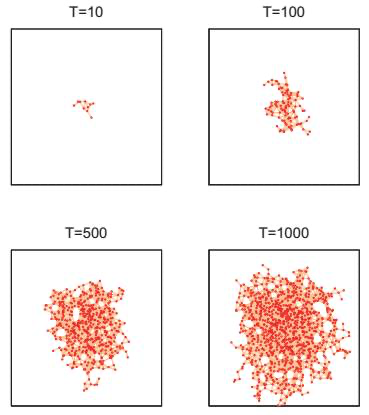
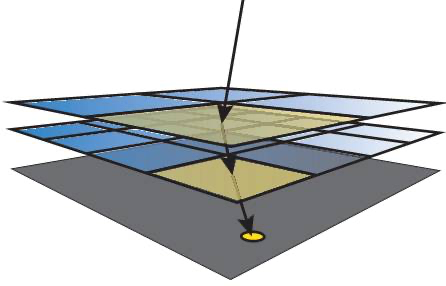
初始时,向一个n维空间中投入一点,那么,在此点周围半径r空间内的,接收新点的概率便会增加,具体某一点接收新点的概率正比于其半径r空间内已有点的总和。不断地向其中添加新的点,同时,将距离小于等于r的点都用边连起来,可以得到一个网络6:
上图表示不同时间上,点生长的结果。
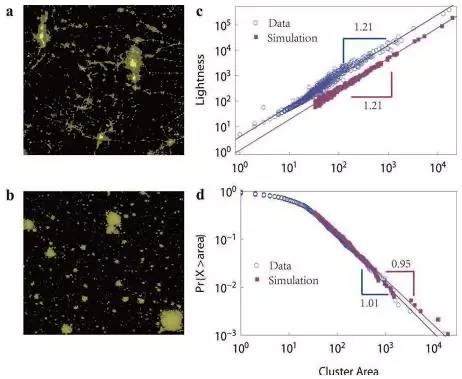
此规则可以模拟与空间位置有关的随机连接,例如交通网络、社交网络(属于抽象空间)。在原文之中,作者使用美国东部的电力网络、美国夜空亮度分布,与此网络的点密度比较,得到了非常好的吻合结果:
上图中,规则稍有改变,投入的任意点,有一定概率pp可以被直接接受,以此可以模拟城市生长。将其与实际数据比较,其光度分布吻合得非常好。
此模型可以较好地模拟很多实际结构,而将Ising模型作用在此网络上,则可以得到例如舆情的多样性、变化、交互的过程与动力学。对于基于“从众”规则的社会模型,也有独到的解释。而此模型与很多固体生长过程颇为类似,亦有望使用在此类过程之中。
注意,这里的随机几何图模型并不是小世界网络7,其度分布不是幂率下降的,但密度分布是幂率下降的。其度分布是:
其中
式中,dd是维度,VdVd是dd维球体积之系数,N(t)N(t)是总颗粒数8.
初步结果
算法概述
由于此规则所产生的概率密度分布较为复杂,所以实际的抽样过程,使用两步法,第一步,是使用四叉树将二维点存入各个树枝之中,这样可以快速地查询一个点周边的邻居,且可以很容易地忽略距离太远的点:
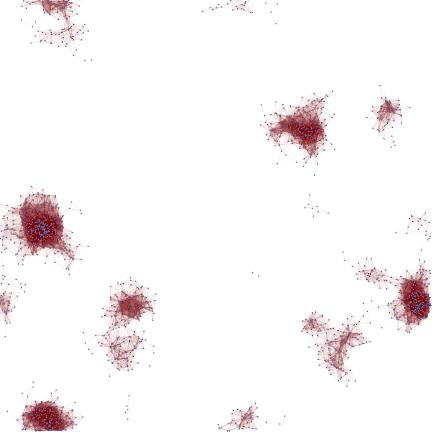
对于每一层的每一个节点,都动态地改变其概率权值。然而这样的过程并不完善,需要进一步地进行抽样,这里使用Metroplis方法,进行随机行走,从而最终逼近其概率分布。这里使用前面生成城市的策略,最终的网络如下:
注意到其中有两个集团之间,虽然是相连的,但又有明显的距离,后面会专门构造此类网络进行分析。
之后的Ising模型运算之中,每个点的邻居用链表储存,且它们是等权的。这里的另一个要求是,它们产生的能量也是直接相加,而不是归一化的:
这意味着,更多的邻居会对此点产生更强的影响。这是符合实际的。
Ising模型的初步结果
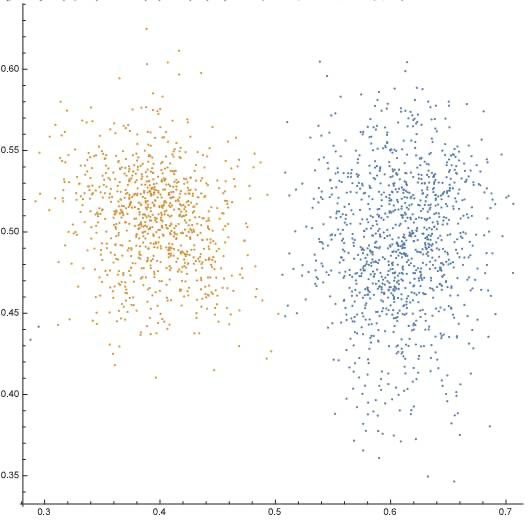
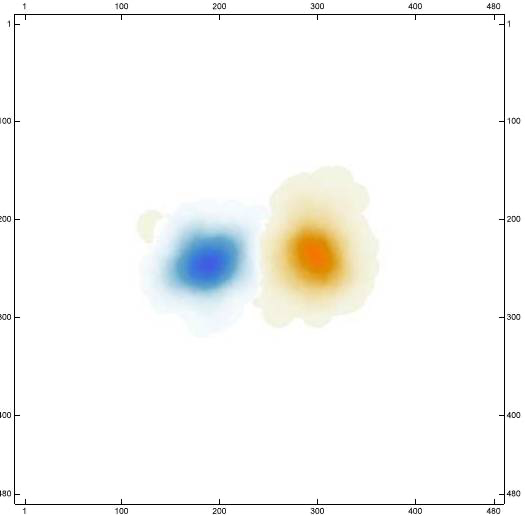
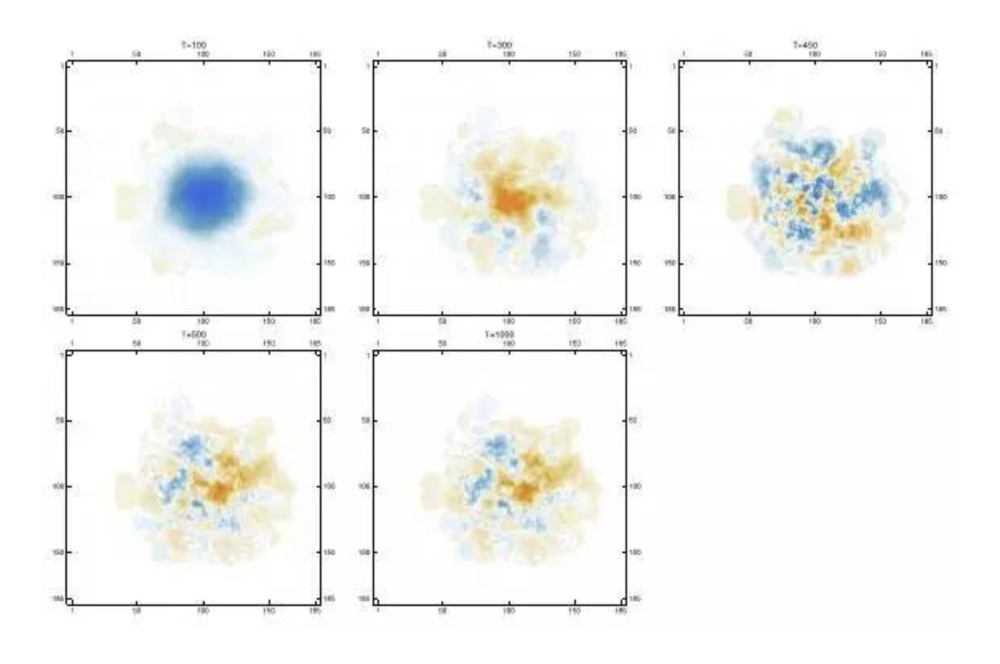
我们使用橙色代表自旋为1的,蓝色代表自旋为-1的点,并对其做模糊,从而有如下的图像:
可以看到,前面特别注意的两个相邻的点,虽然有连接,但仍然可以保持各自的自旋,在运行足够长时间后,仍然稳定。这里猜测此模型之中,可能不会出现各态历经,而是类似于玻璃态的情况。
邻近相连集团的关联性分析
如前面所述,邻近且相连的集团之间,其行为与一般的Ising模型不同,虽然有相互作用,但仍然能保持各自的自旋,这里特别构造出理想结构,进行分析。
在TcTc以下,此处取J/kT=1.0J/kT=1.0,先在(0.4,,0.5)(0.4,,0.5)与(0.6,,0.5)(0.6,,0.5)处设定一些点,以使得最终生长出两个邻近且有相互作用的集团。经过选择随机数种子,得到了如下的生长结果:
其密度图如下所示:
经过数值计算,两边的集团体量是均等的。这样,对于每一次Ising模型的模拟,都使用此图,那么两个计算最终的自旋只有如下四种情形:
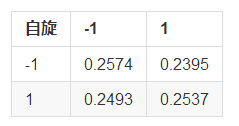
对其进行10000次随机模拟,可以得到上面四种情形的分布。其结果如下:
可以看到,各个情形的数值,基本在0.25左右。有些许偏移,但与一般模型下的Ising模型差别非常大,从而,从相关性的角度来看,邻近集团各自的自旋,相关性很低,可以看做近独立的。
若从理论出发,定性地分析,可以将各个集团核心区域看做高维空间的Ising模型,从实际数据来看,中心附近的点,其连边数n∼100n∼100,而等效的维度d=n/2,从而,其中心部分维度可以近似的等效为一个几十维空间的Ising模型,这时其临界温度很高,而对于外界干扰的稳定性也很强。从另一个角度出发,假设一方的自旋“侵入”另一方,而这个模型中,边缘点的度比中心点的度要少,那么“侵入”的自旋,从概率上,是难以敌过核心区“更固执的自旋”的。
从能量来分析,其分界处,粒子的连边数较少,翻转所需的能量最少,故在此模型中,分界处的变化最丰富。但若要让另一边也发生翻转,则需越过一个能量高峰,这在低温时是无法达到的。
下面考虑单个集团的行为。
单个集团的行为
对于此网络的性质,从单个集团开始分析是比较简单与方便的。
定义磁化率:
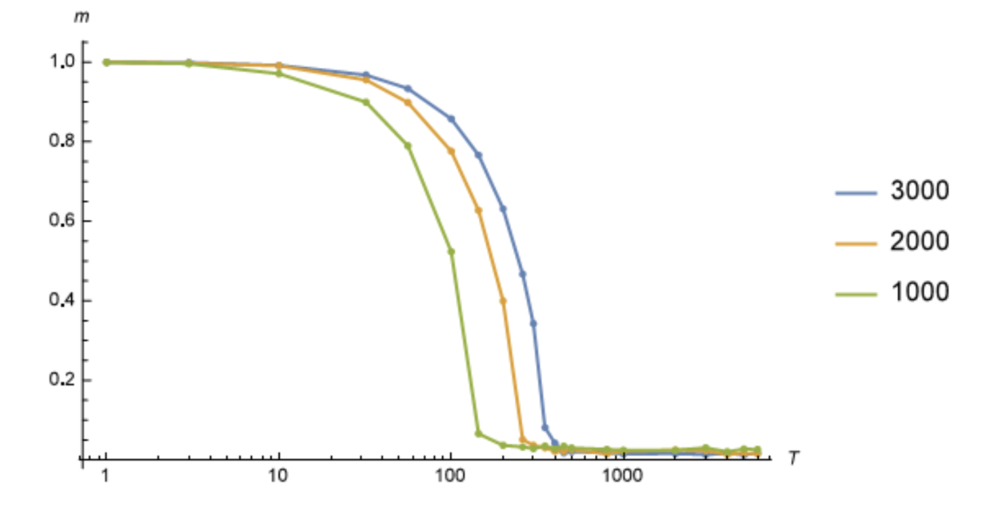
对不同的温度进行计算,在总点数N=3000,,2000,,1000N=3000,,2000,,1000的情况下,其m−Tm−T曲线如下:
可以明显地发现,其有临界相变现象,但阈值各不相同,与总点数N相关。其趋势是N越大,T越大。而从引言中给出的度分布,也可以看出,随着总点数的增加,其平均度是增加的。下图选取了几个典型的温度,在N=2000时迭代100次后的结果:
从上面来看,图中仍然有一些稳定的细节,这是因为点密度不同的区域,其临界温度是不一样的,有可能在温度很高的情形下,依旧能够保持其自旋的稳定。
讨论
此模型具有实际之意义,首先是对真实的社交网络行为,可以进行一定程度的模拟(Barabási的优先连接实现的条件是,新进入的节点能获得所有其他点的信息,这是难以做到的)。而使用Ising模型后,其中的一些行为也是值得研究的。
首先是邻近集团具有较强的独立性,这意味着,只要集团核心区域的密度比邻近地区密度大一些,两者就可以保持独立。这在一些化学生长过程中,可以解释一些具体的行为。而对于我国南方地区,方言的分布也有解释意义。
对于其临界温度,可以看到其与总粒子数密切相关。临界温度越高,意味着越有可能发生自发的磁化。对于之前的城市模型来说,若点越密集,越可能发生“同质化”的现象,核心的影响力亦越大。同时,也暗示了进入连接密度高的社群的个体,更容易受到此社群的影响。
目前的研究还处于非常初步的阶段。首先,对于温度、外场综合的研究尚未完成;其次,计算机模拟的次数较少,算得的一些值的精度不高。另一个方面,为了体现其现实意义,当需与真实的数据做出一些比较。这三个方面,若今后想进一步推进此研究,是可以继续探索的。
参考文献
- 周涛, 柏文洁, 汪秉宏, 刘之景, and 严钢, “复杂网络研究概述,” PHYSICS, vol. 34, no. 1,pp. 31–36, 2005. [Online]. Available:http://d.wanfangdata.com.cn/Periodical/wl200501007
- 周涛, 柏文洁, 汪秉宏, 刘之景, and 严钢, “复杂网络研究概述,” PHYSICS, vol. 34, no. 1,pp. 31–36, 2005. [Online]. Available:http://d.wanfangdata.com.cn/Periodical/wl200501007
- A.-L. Barabási and R. Albert, “Emergence of Scaling in Random Networks,” Science,vol. 286, no. 5439, pp. 509–512, Oct. 1999. [Online]. Available:http://www.sciencemag.org/content/286/5439/509
- D. Brockmann and D. Helbing, “The Hidden Geometry of Complex & Network-Driven Contagion Phenomena,” Science, vol. 342,no.6164, pp. 1337–1342, Dec. 2013. [Online]. Available: http://www.sciencemag.org/cgi/doi/10.1126/science.1245200
- J. Zhang, X. Li, X. Wang, W.-X. Wang, and L. Wu, “Scaling behaviours in the growth of networked systems and their geometric origins,” Scientific Reports, vol. 5, p. 9767,Apr. 2015. [Online]. Available: http://www.nature.com/doifinder/10.1038/srep09767
- J. Zhang, “Growing Random Geometric Graph Models of Super-linear Scaling Law,” ArXiv eprints, Dec. 2012.
- D. Brockmann and D. Helbing, “The Hidden Geometry of Complex & Network-Driven Contagion Phenomena,” Science, vol. 342,no.6164, pp. 1337–1342, Dec. 2013. [Online]. Available: http://www.sciencemag.org/cgi/doi/10.1126/science.1245200
- J. Zhang, X. Li, X. Wang, W.-X. Wang, and L. Wu, “Scaling behaviours in the growth of networked systems and their geometric origins,” Scientific Reports, vol. 5, p. 9767,Apr. 2015. [Online]. Available: http://www.nature.com/doifinder/10.1038/srep09767