拐点

Plot of

y = x 3

的函数图像，(0,0)是其拐点，也是驻点

在微分和微分几何中，拐点（英文名为inflection point，point of infection，flex，或者inflection）是光滑平面曲线上的曲率符号改变的点。在函数图像中，拐点处函数从下凹变为上凸，或从上凸变为下凹。

对于微分类 $C 2$ 的函数的图形（ $f$ ，其一阶导数f'和其二阶导数 f存在且连续），条件f = 0也可用于找到拐点因为必须传递f = 0的点以将f从正值（向上凹）更改为负值（向下凹），反之亦然，因为f是连续的；曲线的拐点是f = 0并在该点改变其符号（从正到负或从负到正）。^[1]其中，第二导数消失，但不改变其正负号的点有时被称为起伏的点或起伏点。

例如，若曲线 $y = f (x)$ 有二阶导数，那么拐点处曲线二阶导数 f'' 为0（f'' =0），并且符号改变（从正到负或从负到正）^[1] 。二阶导数为0但其符号不变的点有时称为波动点 point of undulation。

在代数几何中，拐点的定义更为广泛一些，如切线与曲线相切的正则点至少为3，波动点或超高频点则定义为切线与曲线相交处至少为4。

定义

在微分几何中，拐点是曲率符号改变的点。^[2]^[3]

例如，当且仅当可微函数 $f$ 的一阶导数 $f'$ 在 $x$ 处具有孤立极值时（而不是极值），函数在 $(x, f (x))$ 处有拐点。也就是说，在某些邻域中， $x$ 是 $f'$ 具有（局部）最小值或最大值的唯一点。如果所有 $f'$ 的极值都是孤立的，那么拐点就是 $f$ 曲线图上切线穿越曲线的点。

下降拐点的两边导数都为负，即在该点附近函数值变小。上升拐点的两边导数都为正，即在该点附近函数值变大。

对于一条代数曲线，当且仅当切线与曲线（在切点处）的交点数大于2时，非奇点为拐点。^[4]

其主要结果是代数曲线拐点的集合与曲线同黑塞曲线 (Hessian curve) 的交点集合一致。

对于由参数方程组给出的光滑曲线，若某点处曲率符号改变（从正变为负或从负变为正），则该点就是拐点。

对于一条二次可微函数的光滑曲线，拐点是的二次导数具有孤立零值并且改变曲率符号的点。

f (x) = sin(2 x)

从[math]\displaystyle{ \pi /4 }[/math]到[math]\displaystyle{ 5 \pi /4 }[/math]; 该函数二阶导数为[math]\displaystyle{ {f}''(x) = –4sin(2x) }[/math], 和

f

符号相反。曲线为凸时（函数在切线上方）切线颜色为蓝色，曲线为凹时（函数在切线下方）切线颜色为绿色，拐点颜色为红色：0, [math]\displaystyle{ \pi /2 }[/math] 和 [math]\displaystyle{ \pi }[/math]

必要非充分条件

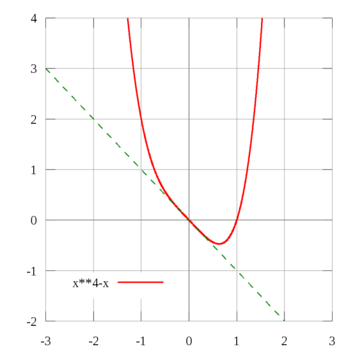
如果二阶导数 $f" (x)$ 在点 $x 0$ 处存在，且 $x 0$ 是该函数的拐点，那么 $f" (x 0) = 0$ 。然而，即使存在任意阶的导数，这也只是拐点的必要非充分条件。在这种情况下，若最低阶(第二阶以上)非零导数为奇数阶(第三阶、第五阶等)，则该点是拐点；若最低阶非零导数为偶数阶，则该点不是拐点，而是波动点。但在代数几何中，波动点也是拐点。例如，函数 $f (x) = x 4$ 的波动点是 $x = 0$ 。

前面我们假定 $f$ 在 $x$ 处存在高阶非零导数，但并不一定存在。如果 $f$ 在 $x$ 处存在高阶非零导数，第一个非零导数有奇数阶意味着[math]\displaystyle{ {f}'(x) }[/math]的符号在某邻域的任一边都是相同的。如果符号为正，那么这个点就是上升拐点；如果符号为负，那么这个点就是下降拐点。

拐点充分条件:

1）第一充分条件：设函数在点 $x$ 的某邻域 $k$ 阶连续可微， $k$ 为奇数且 $k \geq 3$ ，若 $f (n) (x 0) = 0$ ( $n = 2, \dots, k - 1$ ) 且 $f (k) (x 0) \neq 0$ ，那么点 $x 0$ 是 $f (x)$ 的拐点。

2）第二充分条件： $f" (x + ε)$ 和 $f" (x - ε)$ 在x邻域符号相反。

拐点的分类

y = x 4 - x

,x在点 (0,0) 处二阶导数为0，但 (0,0) 不是拐点，因为其四阶导数是一阶非零导数（三阶导数也是零）。

拐点也可以根据[math]\displaystyle{ {f}'(x) }[/math]是否为0来进行分类。

若[math]\displaystyle{ {f}'(x) }[/math]为0，该点为驻点拐点。
若[math]\displaystyle{ {f}'(x) }[/math]不为0，该点为非驻点拐点。

驻点拐点不是局部极值点。在多实变量函数中，不是局部极值点的驻点通常被称为鞍点。

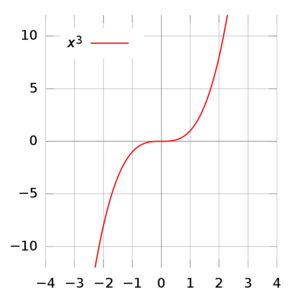
驻点拐点例子： $(0, 0)$ 为函数 $y = x 3$ 的驻点。切线为 $x$ 轴，在 $(0, 0)$ 与函数相切。

非驻点拐点例子： $(0, 0)$ 为函数 $y = x 3 + ax$ 的非驻点（ $a$ 为任意非零常数）。切线为 $y = ax$ ，在 $(0, 0)$ 与函数相切。

非连续函数

有些函数虽然没有拐点但也可改变凹度。这些函数可以通过改变垂直渐近线或非连续性来改变凹度。例如，函数[math]\displaystyle{ x\mapsto \frac1x }[/math] 在函数值 $x$ 为负时显凹性，在函数值 $x$ 为正时显凸性。但这个函数不具有拐点，因为0不在其定义域内。

另见

临界点

海塞配置 Hesse configuration 被椭圆曲线上九个拐点所组成

S形曲线，具有一个拐点的建筑型式曲线

顶点（曲线），曲线的局部最小或局部最大值点

参考文献

↑ ^1.0 ^1.1 Stewart, James (2015). Calculus (8 ed.). Boston: Cengage Learning. pp. 281. ISBN 978-1-285-74062-1.
↑ Problems in mathematical analysis. Baranenkov, G. S.. Moscow: Mir Publishers. 1976 [1964]. ISBN 5030009434. OCLC 21598952.
↑ Bronshtein; Semendyayev (2004). Handbook of Mathematics (4th ed.). Berlin: Springer. p. 231. ISBN 3-540-43491-7.
↑ "Point of inflection". encyclopediaofmath.org.

编者推荐

集智课程

用 Julia 求解微分方程

本次分享将介绍Julia求解微分方程的部分基础生态，主要重点将是常微分方程求解器的类型和构造，也会略微简介少量其他相关类型的微分方程，例如微分代数方程和一些含时偏微分方程。

Julia 积分与微分方程

本次报告中，张润发将介绍如何使用 NeuralPDE 来快速简洁地求解偏微分方程，积分微分方程。这将广泛的应用于数学物理，量子力学，电磁学，光学，等离子体等领域。

集智文章

复杂性科学思维：当你看到拐点时，已来不及

本中文词条由Typhoid翻译，薄荷编辑，如有问题，欢迎在讨论页面留言。

本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

[:0-1] 1.0 ^1.1 Stewart, James (2015). Calculus (8 ed.). Boston: Cengage Learning. pp. 281. ISBN 978-1-285-74062-1.

[:1-2] Problems in mathematical analysis. Baranenkov, G. S.. Moscow: Mir Publishers. 1976 [1964]. ISBN 5030009434. OCLC 21598952.

[:2-3] Bronshtein; Semendyayev (2004). Handbook of Mathematics (4th ed.). Berlin: Springer. p. 231. ISBN 3-540-43491-7.

[4] "Point of inflection". encyclopediaofmath.org.

[1]

[2]

[3]

[4]

拐点

目录

定义