条件随机场
随机场(RF)
在概率论中,由样本空间[math]\displaystyle{ \Omega }[/math]任意取样构成的随机变量[math]\displaystyle{ X_i }[/math]的集合[math]\displaystyle{ S=\{X_1,X_2, ..., X_n\} }[/math],对所有的[math]\displaystyle{ \omega \in \Omega }[/math]式子[math]\displaystyle{ \pi(\omega) \gt 0 }[/math]均成立,则称[math]\displaystyle{ \pi }[/math]为一个随机场。
马尔可夫随机场(MRF)
当随机变量具有依赖关系时,我们研究随机场才有实际的意义,具有马尔可夫性质的随机变量X_i的全联合概率分布模型,构成马尔可夫随机场。
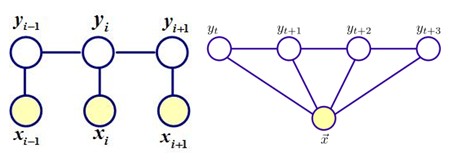
马尔可夫随机场对应一个无向图 [math]\displaystyle{ G=(V, E }[/math])。无向图上的每一个节点[math]\displaystyle{ v \in V }[/math]对应一个随机变量y,俩节点构成的边[math]\displaystyle{ \{u, v\} \in E }[/math] 表示节点对应的随机变量[math]\displaystyle{ y_u, y_v }[/math]之间有概率依赖关系 [math]\displaystyle{ P(y_u|y_v) }[/math],并且依赖关系服从马尔可夫性——离当前因素比较遥远(这个遥远要根据具体情况自己定义)的因素对当前因素的性质影响不大。因此,MRF的结构本质上反应了我们的先验知识——哪些变量之间有依赖关系需要考虑,而哪些可以忽略。
这样我们可以引入团的概念来定义一组具有依赖关系的随机变量[math]\displaystyle{ Y_C }[/math]。若无向图G一个节点集合中任意两个结点{u,v}均有连接,则该集合称为团C,若团C不能加入任意节点且同时满足均有连接的约束,则该团称为最大团。
那么无向图上的联合概率分布P(Y)可写作图中所有最大团C上的函数[math]\displaystyle{ Y_C }[/math]的乘积形式,即:
[math]\displaystyle{ \boldsymbol{P(Y)=\frac{1}{Z} \prod_C \boldsymbol{\Psi}_C(Y_C)} }[/math]
其中[math]\displaystyle{ \boldsymbol{\Psi_C(Y_C)} }[/math]称为势函数,它的定义为:
[math]\displaystyle{ \boldsymbol{\Psi_C(Y_C)=exp\{-E(Y_C)\}} }[/math]
条件随机场(CRF)
如果给定的MRF中每个随机变量y下面还有观察值x,我们要确定的是给定观察集合X下,这个MRF的分布,也就是条件分布,那么这个MRF就称为CRF。它的条件分布形式完全类似于MRF的分布形式,只不过多了一个观察集合X。CRF本质上是给定了观察值 (observations)集合的MRF。
设G=(V,E)是一个无向图,[math]\displaystyle{ \boldsymbol{Y={Y_v|v \in V}} }[/math]是以G中节点v为索引的随机变量Y_v构成的集合,在给定X 的条件下,如果每个随机变量Y_v服从马尔可夫属性,即[math]\displaystyle{ \boldsymbol{p(Y_v|X,Y_u,u \ne v) = p(Y_v|X,Y_u,u \sim v)} }[/math], 则(X,Y)就构成一个条件随机场。注意,定义中并不要求X和Y具有相同结构。
解决序列标注问题我们可以将条件随机场具体化为线性链结构的条件随机场(Linear-chain CRFs),其中X表示输入的观测序列,Y表示对应输出的状态序列。
[math]\displaystyle{ \boldsymbol{P(y_i|x,y_1,...,y_{i-1},y_{i+1},...,y_i)=P(y_i|x,y_{i-1},y_{i+1})} }[/math]
形式化模型
同最大熵模型相似,我们需要先引入特征函数,其中t_k是定义在边上的转移特征,依赖于当前位置y_i和前一位置y_{i-1},s_l是定义在节点上的状态特征,只依赖于当前位置。
[math]\displaystyle{ \boldsymbol{t_k(y_{i-1},y_i,x,i) \in \{0,1\}} }[/math]
[math]\displaystyle{ \boldsymbol{s_l(y_i,x,i) \in \{0,1\}} }[/math]
我们可以将转移特征和状态特征用统一的符号表示,则特征函数f(x,y)的数量等于K+L。
[math]\displaystyle{ \boldsymbol{f_k(y_{i-1},y_i,x,i)=\begin{cases} t_k(y_{i-1},y_i,x,i) & k=1,2,...,K_1 \\ s_l(y_i,x,i) & k=K_1+l;l=1,2,...,K_2 \end{cases}} }[/math]
那么对于每个团Y_i上的势函数[math]\displaystyle{ \Psi_i(Y_i) }[/math]有:
[math]\displaystyle{ \boldsymbol{\Psi_i (Y_i)=exp\left(\sum_{i=1}^n \sum_j \lambda_j f_j(y_{i-1},y_i,x,i)\right)} }[/math]
带入P(Y|X)与Z(X)最终得到,其中n是随机序列X的个数
[math]\displaystyle{ \boldsymbol{p_{\lambda}^*(y|x,\lambda)=\frac{1}{Z_{\lambda}(x)}exp\left(\sum_{i=1}^n \sum_j \lambda_j f_j(y_{i-1},y_i,x,i)\right)} }[/math]
[math]\displaystyle{ \boldsymbol{Z_{\lambda}(x)=\sum_j exp\left(\sum_{i=1}^n \sum_j \lambda_j f_j(y_{i-1},y_i,x,i)\right)} }[/math]
与最大熵马尔可夫模型的比较
对比条件随机场, 最大熵马尔可夫模型公式,可以看出,条件随机场需要计算全局特征向量归一化特征函数的参数向量[math]\displaystyle{ \lambda_i }[/math],用以解决MEMM中的标记偏置问题,但很明显这样也会带来的巨大的计算量。
限域拟牛顿法(L-BFGS)
牛顿法(Newton Method)
首先考虑,微积分中用于求一元函数根的Newton法:
Newton法从第k次近似值x_k求得第k+1次近似值x_k+1即为求x_k点处的切线和x轴的交点,切线方程:
[math]\displaystyle{ y-f(x_k) = \nabla f(x_k)(x-x_k) }[/math] [math]\displaystyle{ \Rightarrow 0-f(x_k) = \nabla f(f_k)(x-x_k) }[/math] [math]\displaystyle{ \Rightarrow \nabla f(x_k)*x = \nabla f(x_k)*x_k- f(x_k) }[/math] [math]\displaystyle{ \Rightarrow x = x_k - f(x_k)/\nabla f(x_k) }[/math]
因此有:[math]\displaystyle{ x_{k+1} = x_k - f(x_k)/\nabla f(x_k) }[/math]
经典牛顿法的基本思想是在极小点附近通过对目标函数做二阶Taylor展开,进而找到的极小点的估计值。考虑最简单的一维情况,即令函数
[math]\displaystyle{ f(x) = f(x_k) + f'(x_k)(x-x_k) + \frac{1}{2}f''(x_k)(x-x_k)^2 }[/math]
则其导数[math]\displaystyle{ \varphi'(x) }[/math]满足
[math]\displaystyle{ \varphi'(x) = f'(x_k) + f''(x_k)(x-x_k) = 0 }[/math]
因此
[math]\displaystyle{ x_{k+1} = x_k-\frac{f'(x_k)}{f''(x_k)} }[/math]
将[math]\displaystyle{ x_{k+1} }[/math]作为[math]\displaystyle{ f(x) }[/math]极小点的一个进一步的估计值。重复上述过程,可以产生一系列的极小点估值集合[math]\displaystyle{ \{x_k\} }[/math]。一定条件下,这个极小点序列[math]\displaystyle{ \{x_k\} }[/math]收敛于的[math]\displaystyle{ f(x) }[/math]极值点。
将上述讨论扩展到N维空间,类似的,对于N维函数[math]\displaystyle{ f(x) }[/math]有
[math]\displaystyle{ f(x) \approx \varphi(x) = f(x_k) + \nabla f(x_k)(x-x_k) + \frac{1}{2}(x-x_k)^T \nabla^2 f(x-x_k) }[/math]
其中[math]\displaystyle{ \nabla f(x_k) }[/math]和[math]\displaystyle{ \nabla^2 f(x) }[/math]分别是目标函数的的一阶和二阶导数,表现为N维向量和[math]\displaystyle{ N \times N }[/math]矩阵,而后者又称为目标函数在处的Hesse矩阵。 设[math]\displaystyle{ \nabla^2 f(x) }[/math]可逆,则可得类似的迭代公式:
[math]\displaystyle{ x_{k+1} = x_k -\frac{\nabla f(x_k)}{\nabla^2 f(x)} }[/math]
这就是原始牛顿法的迭代公式。
原始牛顿法虽然具有二次终止性(即用于二次凸函数时,经有限次迭代必达极小点),但是要求初始点需要尽量靠近极小点,否则有可能不收敛。因此人们又提出了阻尼牛顿法。这种方法在算法形式上等同于所有流行的优化方法,即确定搜索方向,再沿此方向进行一维搜索,找出该方向上的极小点,然后在该点处重新确定搜索方向,重复上述过程,直至函数梯度小于预设判据。具体步骤列为算法1。
算法1: (1) 给定初始点[math]\displaystyle{ x_0 }[/math],设定收敛判据[math]\displaystyle{ \varepsilon }[/math],k = 0.
(2) 计算[math]\displaystyle{ \nabla f(x_k) }[/math]和[math]\displaystyle{ \nabla^2 f(x) }[/math].
(3) 若[math]\displaystyle{ \Vert \nabla f(x_k) \Vert \lt \varepsilon }[/math] ,则停止迭代,否则确定搜索方向[math]\displaystyle{ d_k = -\frac{\nabla f(x_k)}{\nabla^2 f(x)} }[/math].
(4) 从[math]\displaystyle{ x_k }[/math]出发,沿[math]\displaystyle{ d_k }[/math]做一维搜索,
[math]\displaystyle{ \min_{\lambda} f(x_k + \lambda d_k) = f(x_k + \lambda_k d_k) }[/math],
令[math]\displaystyle{ x_{k+1} = x_k + \lambda_k d_k }[/math]
(5) 设[math]\displaystyle{ k = k+1 }[/math],转步骤(2).
在一定程度上,阻尼牛顿法具有更强的稳定性。
拟牛顿法 (Quasi-Newton Method)
牛顿法虽然收敛速度快,但是计算过程中需要计算目标函数的二阶偏导数,难度较大。更为复杂的是目标函数的Hesse矩阵无法保持正定,从而令牛顿法失效。为了解决这两个问题,人们提出了拟牛顿法。这个方法的基本思想是不用二阶偏导数而构造出可以近似Hesse矩阵的逆的正定对称阵, 从而在"拟牛顿"的条件下优化目标函数。构造方法的不同决定了不同的拟牛顿法。
首先分析如何构造矩阵可以近似Hesse矩阵的逆:
设第k次迭代之后得到点[math]\displaystyle{ x_{k+1} }[/math],将目标函数[math]\displaystyle{ f(x) }[/math]在[math]\displaystyle{ x_{k+1} }[/math]处展成Taylor级数,取二阶近似,得到
[math]\displaystyle{ f(x) \approx f(x_{k+1}) + \nabla f(x_{k+1})(x-x_{k+1}) + \frac{1}{2}(x-x_{k+1})^T \nabla^2 f(x_{k+1})(x-x_{k+1}) }[/math]
因此
[math]\displaystyle{ \nabla f(x) \approx \nabla f(x_{k+1}) + \nabla^2 f(x_{k+1})(x-x_{k+1}) }[/math]
令[math]\displaystyle{ x = x_k }[/math],则
[math]\displaystyle{ \nabla f(x_{k+1}) - \nabla f(x_k) \approx \nabla^2 f(x_{x+1})(x_k - x_{k+1}) (1) }[/math]
记
[math]\displaystyle{ s_k = x_{k+1} - x_k, y_k = \nabla f(x_{k+1}) - \nabla f(x_k) }[/math]
同时设Hesse矩阵[math]\displaystyle{ \nabla^2 f(x_{k+1}) }[/math]可逆,则方程(1)可以表示为
[math]\displaystyle{ s_k \approx [\nabla^2f(x_{k+1})]^{-1}y_k (2) }[/math]
因此,只需计算目标函数的一阶导数,就可以依据方程(2)估计该处的Hesse矩阵的逆。也即,为了用不包含二阶导数的矩阵
[math]\displaystyle{ H_{k+1} }[/math]近似牛顿法中的Hesse矩阵[math]\displaystyle{ \nabla^2 f(x_{k+1}) }[/math]的逆矩 阵,[math]\displaystyle{ H_{k+1} }[/math]必须满足
[math]\displaystyle{ s_k \approx H_{k+1}y_k (3) }[/math]
方程(3)也称为拟牛顿条件。
下面给出两个最常用的[math]\displaystyle{ H_{k+1} }[/math]构造公式
DFP公式
设初始的矩阵[math]\displaystyle{ H_0 }[/math]为单位矩阵[math]\displaystyle{ I }[/math],然后通过修正[math]\displaystyle{ H_k }[/math]给出[math]\displaystyle{ H_{k+1} }[/math],即
[math]\displaystyle{ H_{k+1}=H_k + \Delta H_k }[/math]
DFP算法中定义校正矩阵为
[math]\displaystyle{ \Delta H_k = \frac{s_k s^T_k}{s^T_k y_k}- \frac{H_k y_k y^T_k H_k}{y^T_k H_k y_k} }[/math]
因此
[math]\displaystyle{ H_{k+1} = H_k + \frac{s_k s^T_k}{s^T_k y_k}- \frac{H_k y_k y^T_k H_k}{y^T_k H_k y_k} (4) }[/math]
可以验证,这样产生的[math]\displaystyle{ H_{k=1} }[/math]对于二次凸函数而言可以保证正定,且满足拟牛顿条件。
BFGS公式
BFGS公式有时也称为DFP公式的对偶公式。这是因为其推导过程与方程(4)完全一样,只需要用矩阵[math]\displaystyle{ B_{k+1} }[/math]取代[math]\displaystyle{ H^{-1}_{k+1} }[/math],同时将[math]\displaystyle{ S_k }[/math]和[math]\displaystyle{ y_k }[/math] 互换,最后可以得到
[math]\displaystyle{ H_{k+1} = H_k + [1+\frac{y^T_k H_k y_k}{s^T_k y_k}] \cdot \frac{s_k s^T_k}{s^T_k y_k} - \frac{s_k y^T_k H_k}{S^T_k y_k} (5) }[/math]
这个公式要优于DFP公式,因此目前得到了最为广泛的应用。
利用方程(4)或(5)的拟牛顿法计算步骤列为算法2。
算法2: (1) 给定初始点[math]\displaystyle{ x_0 }[/math],设定收敛判据 [math]\displaystyle{ \epsilon }[/math],[math]\displaystyle{ k = 0 }[/math].
(2) 设[math]\displaystyle{ H_0 = I }[/math],计算出目标函数[math]\displaystyle{ f(x) }[/math]在[math]\displaystyle{ x_k }[/math]处的梯度[math]\displaystyle{ g_k = \nabla f(x_k) }[/math].
(3) 确定搜索方向[math]\displaystyle{ d_k }[/math]:[math]\displaystyle{ d_k = H_k g_k }[/math].
(4) 从[math]\displaystyle{ x_k }[/math]出发,沿[math]\displaystyle{ d_k }[/math]做一维搜索,满足
[math]\displaystyle{ f(x_k + \lambda_k d_k) = \min_{\lambda \ge 0}f(x_k + \lambda d_k) }[/math]
令[math]\displaystyle{ x_{k+1} = x_k + \lambda_k d_k }[/math].
(5) 若[math]\displaystyle{ \Vert f(x_{k+1} \Vert \le \epsilon) }[/math],则停止迭代,得到最优解[math]\displaystyle{ x = x_{k+1} }[/math],否则进行步骤(6).
(6) 若[math]\displaystyle{ k = N-1 }[/math],则令x_0 = x_{k+1},回到步骤(2),否则进行步骤(7). (7) 令[math]\displaystyle{ g_{k+1} = f'(x_{k+1}) }[/math],[math]\displaystyle{ s_k = x_{k+1} - x_k }[/math],y_k = g_{k+1}-g_k,利用方程(4)或(5)计算[math]\displaystyle{ H_{k+1} }[/math],设[math]\displaystyle{ k = k+1 }[/math],回到步骤(3)。
LBFGS Method
算法2的步骤(3)中,为了确定第 k 次搜索方向,需要知道对称正定矩阵[math]\displaystyle{ H_k }[/math],因此 对于 N 维的问题,存储空间至少是[math]\displaystyle{ N(N+1)/2 }[/math],对于大型计算而言,这显然是一个极大的缺点。作为比较,共轭梯度法只需要存储3个 N 维向量。为了解决这个问题,Nocedal首次提出了基于BFGS公式的限域拟牛顿法(L-BFGS)[2]。
L-BFGS的基本思想是存储有限次数(如m次)的更新矩阵[math]\displaystyle{ \delta{H_k} }[/math],如果k > m的话就舍弃m次以前的[math]\displaystyle{ \delta H_{k-m+1} }[/math],也即L-BFGS的记忆只有M次。如果[math]\displaystyle{ m = N }[/math],则L- BFGS等价于标准的BFGS公式。
首先将方程(5)写为乘法形式:
[math]\displaystyle{ H_{k+1} = (I-\rho_k s_k y^T_k) H_k (I- \rho_k y_k s^T_k) + \rho_k s_k s^T_k = v^T_k H_k v_k + \rho_k s_k s^T_k }[/math] (6)
其中[math]\displaystyle{ \rho_k = \frac{1}{y^T_k s_k} }[/math],[math]\displaystyle{ v_k }[/math]是 [math]\displaystyle{ N \times N }[/math] 的矩阵。乘法形式下"舍弃"等价于置[math]\displaystyle{ V_k = I }[/math],[math]\displaystyle{ \rho_k = 0 }[/math]。容易得出,给定M后,BFGS的矩阵更新可以写为
若[math]\displaystyle{ k+1 \le m }[/math],则
[math]\displaystyle{ H_{k+1} = v^T_k v^T_{k-1} ... H_0v_0... v_{k-1}v_k + v^T_k ... v^T_1 \rho_0 s_0 s^T_0 v_1 ...v_k }[/math] [math]\displaystyle{ + v^T_k v^T_{k-1}...v^T_2 \rho_1 s_1s^T_1 v_2 ... v_k }[/math] [math]\displaystyle{ ... }[/math] [math]\displaystyle{ + v^T_k v^T_{k-1} \rho_{k-2} s_{k-2} s^T_{k-2} v_{k-1} v_k }[/math] [math]\displaystyle{ + v^T_k \rho_{k-1} s_{k-1} s^T_{k-1} v_k }[/math] [math]\displaystyle{ \rho_k s_k s^T_k (9) }[/math]
若 [math]\displaystyle{ k+1 \gt m }[/math] ,则
[math]\displaystyle{ H_{k+1} = v^T_k v^T_{k-1} ... v^T_{k-m+1} H_0 v_{k-m+1} ... v_{k-1} v_k }[/math] [math]\displaystyle{ +v^T_k ... v^T_{k-m+2} \rho_{k-m+1} s^T_{k-m_1} v_{k-m_2} ... v_k }[/math] [math]\displaystyle{ ... }[/math] [math]\displaystyle{ +v^T_k \rho_{k-1} s_{k-1} s^T_{k-1} v_k }[/math] [math]\displaystyle{ +\rho_k s_k s^T_k (10) }[/math]
方程(9)和(10)称为狭义BFGS矩阵(special BFGS matrices)。仔细分析这两个方程以及[math]\displaystyle{ \rho_k }[/math]和[math]\displaystyle{ v_k }[/math]的定义,可以发现L-BFGS方法中构造[math]\displaystyle{ H_{k+1} }[/math]只需要保留[math]\displaystyle{ 2m+1 }[/math]个[math]\displaystyle{ N }[/math]维向量:[math]\displaystyle{ m }[/math]个[math]\displaystyle{ s_k }[/math]、[math]\displaystyle{ m }[/math]个[math]\displaystyle{ y_k }[/math]以及[math]\displaystyle{ H_0 }[/math](对角阵)。
快速计算[math]\displaystyle{ H \cdot g }[/math]
L-BFGS算法中确定搜索方向[math]\displaystyle{ d_k }[/math]需要计算[math]\displaystyle{ H \cdot g }[/math],下列算法可以高效地完成计算任务:
算法3: IF [math]\displaystyle{ k \le m }[/math] Then
[math]\displaystyle{ incr = 0; BOUND = k }[/math]
ELSE
[math]\displaystyle{ incr = k-m; BOUND = m }[/math]
ENDIF
[math]\displaystyle{ q_{BOUND} = g_k }[/math];
DO [math]\displaystyle{ i = (BOUND-1), 0, -1 }[/math]
[math]\displaystyle{ j = i + incr }[/math]; [math]\displaystyle{ \alpha_i = \rho_j s^T_j q_{i + 1} }[/math]; 储存[math]\displaystyle{ \alpha_i }[/math]; [math]\displaystyle{ q_i = q_{i+1} - \alpha_i y_j }[/math];
ENDDO
[math]\displaystyle{ r_0 = H_0 \cdot g_o }[/math];
DO [math]\displaystyle{ i = 0, (BOUND-1) }[/math]
[math]\displaystyle{ j = i + incr }[/math]; [math]\displaystyle{ \beta_j = \rho_j y^T_j r_i }[/math]; [math]\displaystyle{ r_{i+1} = r_i + s_j(\alpha_i - \beta_i) }[/math];
ENDDO
弹性反向传播(RPROP)
参考文献
- 李航, 统计学习方法
- Roman Klinger, Katrin Tomanek, Classical Probabilistic Models and Conditional Random Fields