树的异速标度律
所谓树的异速标度律是指Ci和Ai之间的幂律关系:
[math]\displaystyle{ C_i=cA_i^{\eta} }[/math]
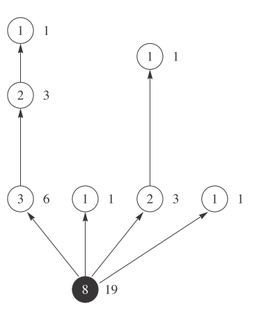
其中Ai是指以任意节点i为根的子树所包含的节点的个数,而Ci则是指该子树上所有节点的Aj之和,即:
[math]\displaystyle{ C_i=\sum_{j\in Tree_i}A_j }[/math]
其中Treei表示以i为根的子树。c为一常数,η为异速标度律指数,它表示该树的垂直化程度。若整个树越扁平,则η指数越小,反之η越大。
右图展示了一棵树的实例,每个节点的Ai写在了节点中,而Ci则写到了每个节点的旁边。
链和星状结构
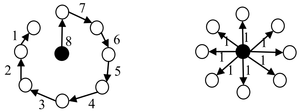
为了展示η指数与树的扁平化程度之间的关系。我们来看两个极端的例子,一个是星型的网络,它是一种极端的扁平化结构,另外一个是一条链,它是一种极端的垂直的结构[1]。
假设树中的节点总数就是N,对于左图链状结构来说,从尾端数第i个节点的:
[math]\displaystyle{ A_i=i }[/math]
该节点的Ci为:
[math]\displaystyle{ C_i=\sum_{j=1}^i A_j=\sum_{j=1}^ij=\frac{j(j+1)}{2}=\frac{A_i(A_i+1)}{2}\sim A_i^2 }[/math]
因此,链状网络的异速标度律指数为2。而对于星型节点来说,所有叶节点的Ai=Ci=1,但是树根的
[math]\displaystyle{ A_i=N }[/math]
而:
[math]\displaystyle{ C_i=N+1\times N=2N=2A_i\sim A_i }[/math]
所以,对于星形树来说,异速标度律指数η=1。对于更一般的树,它一定介于完全的链状结构和星型结构之间,因此幂律指数η就介于1和2之间。
生成树的异速标度律
Frank和Murrell等人更进一步地探索了树状结构与异速标度律指数之间的关系[2]。首先,它们构建了一个简单的随机生成树模型,该模型模拟了树的随机生长。该模型有两个参数β和θ,它们控制了整个树的形状。β控制的是与根节点直接相连的节点占总节点数的比例,θ控制的是树的平均深度。
首先,让βN个节点附着在根节点上,形成第一层节点; 然后,在每一时刻,就会有一个节点加入该树状结构中,其中这个新加节点j会随机地附着在某一个该树上的节点i上作为i的子节点,那么,附着在i上的概率由i所在树的深度决定,即按照概率:
[math]\displaystyle{ P_{ij}=\frac{t_i^{-\theta}}{\sum_{k\in Tree}t_k^{-\theta}} }[/math]
其中tk表示k节点所在的深度。也就是说j会优先附着在ti-θ较大的节点上。如果θ越大,则j更偏好离根较近的节点,反之则更倾向于附着在较深的节点上。 所以如果θ越大,β越小,就会得到越深的树。
下面,我们来看两棵由模型生成的树(β相同,都为0.1):
接下来,我们就可以变换不同的θ和β的组合而创造不同的树结构,并计算出这些树的η数值[2]。
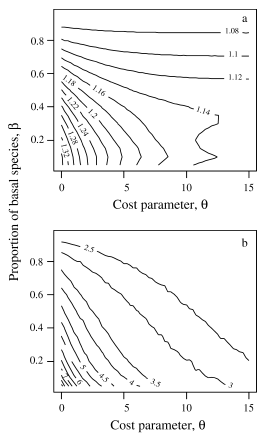
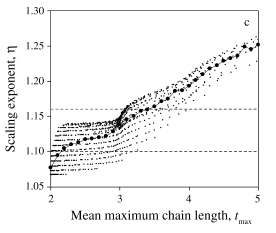
这是2张等高线图,其中横坐标和纵坐标分别为θ和β,等高线标示了η(上)和平均路径长度(下,也就是树的平均深度)。可以看出,随着θ的升高,η在变小,同时平均路径长度在变小,这说明树在变得不断地扁平。同时,随着β的升高,η和平均路径长度也在变小。由此可以看出,实际上η和平均路径长度是正相关的,如下图[2]:
η的含义
在文章[3]和[1]中,作者将η解释为输运树的效率,其中输运效率是指从源(根)到所有节点的平均路径长度。因此,路径越短,整个树越有效率。
如果从扁平化和垂直化的角度来说,η也可以理解为网络的集中性程度。如果将整个树理解为一个公司的组织架构,那么η越大,结构越垂直化,因此权利越集中在树的上层,反过来,树状结构越扁平,权利越分散。
参考文献