流距离
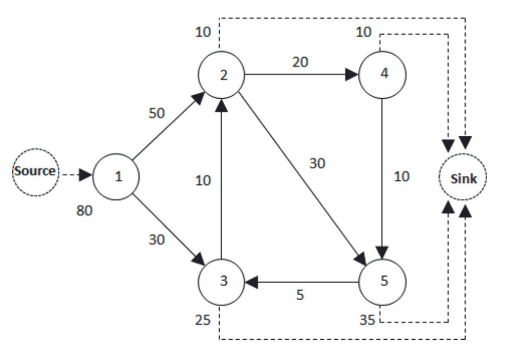
在流网络中,大量的粒子在网络中流动。我们假设单位时间粒子沿着有向连边跳转。这样,粒子需要m个时间步才能走完一条m长的路径。我们感兴趣的是从网络上任意一点i到任意一点j的时间(距离),我们称之为流距离。
首先,由于网络中存在着环路,因此,从i流向j的粒子有可能经历无限长的时间步。为了避免这个问题,我们只考虑首达时间,也就是粒子从i出发第一次到达j的时间。但是,由于粒子可能沿不同的路径到达j,而这些路径的长度又不一样,所以没有确定的首达时间值。于是,我们只能用这些粒子的首达时间值来作为我们研究的目标,也就是平均首达时间。有趣的是,对于平衡的流网络来说,平均首达时间的计算存在着简洁而明确的表达式和计算方法。
任意点i到汇的平均时间
首先,我们来求从任意节点i(不包括汇)出发,到达汇N+1的粒子们的平均首达时间。由于到达N+1的粒子不再流向任何其它节点,因此这个平均首达时间其实就是粒子从i到达N+1的平均时间。下面,我们来计算从i到汇的平均时间。
我们不妨假设从任意节点i到达汇N+1的平均时间为li,那么,我们可以列出如下等式:
-
[math]\displaystyle{ l_i=1+\sum_{j=0}^{N}{m_{ij}l_j}, ~~~~\forall i\neq N+1 }[/math]
(eq2)
下面来解释这个式子。我们知道任何粒子要想跳到汇都有两种可能性:直接跳到N+1,或者先跳到任意一个其他的非汇节点j,然后再跳到汇N+1。对于第一种情况,它的路径长度确定性的是1,发生概率是[math]\displaystyle{ m_{i,N+1} }[/math]。而对于第二种情况,假设粒子跳到了j,再由j跳到N+1,那么我们知道粒子从j跳到N+1的平均首达时间是lj,而粒子跳转到j的概率是mi,j,因此粒子跳到任意的非汇节点,再跳到汇的平均路径长度就是[math]\displaystyle{ \sum_{j=0}^{N}{m_{ij}(1+l_j)} }[/math],其中和号里的式子加1的原因是每条路经长度都要包含从i跳到j的这一步。于是,把这两种可能性合起来就有:
[math]\displaystyle{ l_i=m_{i,N+1}\cdot 1+\sum_{j=0}^{N}{m_{ij}(1+l_j)}=m_{i,N+1}+\sum_{j=0}^{N}m_{ij}+\sum_{j=0}^{N}m_{ij}l_j=1+\sum_{j=0}^{N}m_{ij}l_j, ~~~~\forall i\neq N+1 }[/math]
最后用到了马尔科夫链的归一化条件:[math]\displaystyle{ \sum_{j=0}^{N+1}m_{ij}=1 }[/math]。注意到eq2实际上是一个线性方程组,未知数有N+1个,方程个数也有N+1个,可以直接求解。事实上,如果我们定义:向量[math]\displaystyle{ L=(l_0,l_1,\cdot\cdot\cdot,l_N)^T }[/math],则eq2可以写成矩阵的形式:
[math]\displaystyle{
L=\mu+M_{-(N+1)} L
}[/math]
其中[math]\displaystyle{ \mu=(1,1,\cdot\cdot\cdot,1)^T }[/math],1构成的N+1维列向量。[math]\displaystyle{ M_{-(N+1)} }[/math]表示原始马尔科夫矩阵去掉最后一行和最后一列。则,最终L可以解出:
-
[math]\displaystyle{ L=(I-M_{-(N+1)}^{-1})\cdot \mu=U_{-(N+1)}\cdot \mu=(\sum_{j=0}^{N}u_{ij})_{(N+1)\times 1} }[/math]
(eq3)
其中矩阵U-(N+1)为U矩阵去掉最后一行和最后一列。最后一个等式是根据马尔科夫链删除节点的性质中的定理1得到的。这样L中的第i个元素就是i节点到汇的平均时间。
对于图1所示网络,我们可以计算出[math]\displaystyle{ L=(63/16, 47/16, 175/82, 66/41, 525/328, 197/164) }[/math],其中从源到汇的平均路首达时间是63/16,也就是平均每个粒子经过3.9375步跳出整个网络。它刚好是[math]\displaystyle{ \sum_{j=0}^{N}u_{0j}=\frac{C_0}{T_0}+1=\frac{TST}{IS}+1 }[/math]。这后两个等式需要参考流网络的异速标度律.
从源到任意点i的平均首达时间
我们无法简单套用公式eq3来计算从源到任意点i的平均首达时间[1],这是因为如果将i节点去除,而非N+1,那么整个网络就有可能不连通,使得最后的求解出现问题。但是,我们仍然可以用类似的推理方法:我们假设0到任意i的平均首达时间为li。从源0到任意节点i的路径总可以分成两种情况,要么从0直接到i,要么从0到某个j再到i,于是假设0到j的距离为lj,则第二种情况下的平均首达时间就是:[math]\displaystyle{ \sum_{j=1}^{N+1} m'_{ji}(l_j+1) }[/math]。注意,在这里,马尔科夫转移概率是逆向马尔科夫转移概率m'ji而不再是m了,这是因为我们已经确定性地知道了粒子肯定到达i的情况下,它可能从j节点过来的概率。于是,在这种情况下,概率归一化的对象是给定在i观察到粒子的情况下,从所有可能的中间节点过来的概率。所以,如果使用mji的话,则不能满足概率归一的条件,所以只能用m'ij。最后,再综合第一种情况,就有:
[math]\displaystyle{ l_i=m'_{0,i}+\sum_{j=1}^{N+1} m'_{ji}(l_j+1)=m'_{0,i}+\sum_{j=1}^{N+1} m'_{ji}+\sum_{j=1}^{N+1} m'_{ji}l_j=1+\sum_{j=1}^{N+1}m'_{ji}l_j,~~~~\forall i\neq 0 }[/math]
同样可以把它写作一个矩阵方程:
[math]\displaystyle{ L=\mu+M'_{-0}L }[/math]
于是,求解得:
[math]\displaystyle{ L=(I-M'_{-0})^{-1}\mu=U'_{-0}\mu }[/math]
注意,与eq3相比,我们把M换成了逆向马尔科夫矩阵M'。也就是说,求从源0到任意点i的首达时间问题相当于是把整个流网络倒转过来,把源当成汇,把汇当成源,然后求任意节点i到汇的首达时间问题。
对于图1所示网络,可以计算出: [math]\displaystyle{ L'=(1, 365/164, 193/82, 529/164, 285/82, 63/16) }[/math] 注意,第一个元素对应的是0到1的平均首达时间,……,以此类推。那么0到汇的平均首达时间是63/16,这与上面的计算结果是一致的。
任意节点i到任意节点j的平均首达时间(流距离)
更一般地,我们应如何求出任意点i到j的平均首达时间呢?首先,我们需要明确这个平均首达时间到底是什么意思。还是假设所有流经i点的粒子都被染上了红色,并且粒子一经过j点就被抹掉红色。这样,j点接收的粒子就是首次到达j点的粒子。同时,假设每个粒子都有一个内置的秒表。它一旦被染成红色,秒表就开始计时,每个时间步走动一次。于是我们在j点读出粒子的计时,看它从i出发走了多少时间步过来。由于每个粒子的时间不一样,于是,我们就可以求出一个均值。这就是我们要求的平均首达时间。
如何计算这个平均首达时间呢?上面介绍的方法只适用于源或汇,而不能简单地拓展到非源或汇节点。下面,我们将介绍一种非常简单实用的方法,我称其为级数法。首先,根据平均首达时间的定义,我们知道从i到j的平均首达时间可以写为:
[math]\displaystyle{ l_{i,j}=\sum_{k=1}^{\infty}kp^{k}_{i,j} }[/math]
这里,pki,j是粒子经过k步从i首达j的概率。这个概率怎么求呢?一种直观的想法就是用(Mk)i,j来计算这个数值。但是,这是错误的,因为,pki,j这个概率是指所有那些从i到j首达的粒子中,刚好经过了k步的粒子比例。而(Mk)i,j表达的则是,在所有从i出发经过k步转移后的粒子中,那些刚好到达节点j的粒子比例。这两者显然不一样,因为从i出发的粒子经过k步后不见得都到达j。
让我们只考察到达j的那些粒子,每一时刻,这个流量是固定的,有一些粒子是从i出发首达的粒子,而其中有一部分刚好经历了k步。那么,从i到j的首达粒子就可以用首达流来计算。刚好经过了k步的首达粒子如何计算呢?我们知道Φ0,i(Mk)i,j是所有经过k步转移,从i到j的粒子数。但是这些粒子并不是首达粒子,有一些曾到过j又从j到j的粒子数。为了避免这种重复,我们不妨在M上做一些手脚:我们把M中j节点对应的行都设为0,即,定义:
[math]\displaystyle{ (M_{-j})_{p,q}=\left\{\begin{array}{ll} m_{p,q} & \mbox {if } p\neq j, \\ 0 & \mbox {if } p = j\end{array}\right. }[/math]
这样,概率pki,j就可以这样计算:
[math]\displaystyle{ p^{k}_{i,j}=\frac{\phi_{0i}(M_{-j}^k)_{i,j}}{\phi_{i,j}} }[/math]
于是平均首达时间就变成了求下列无穷级数和:
[math]\displaystyle{ l_{i,j}=\sum_{k=0}^{\infty}k\frac{\phi_{0i}(M_{-j}^k)_{i,j}}{\phi_{i,j}}=\frac{\phi_{0i}(\sum_{k=1}^{\infty}kM_{-j}^k)_{ij}}{\phi_{i,j}} }[/math]
那么,下面的任务就是如何求解无穷级数[math]\displaystyle{ \sum_{k=1}^{\infty}k(M_{-j})^k }[/math]的和。为此,我们设此和为X,则在等式两边右乘以M-j得到:
[math]\displaystyle{ XM_{-j}=\sum_{k=1}^{\infty}kM_{-j}^{k+1}=M_{-j}^2+2M_{-j}^3+\cdot\cdot\cdot }[/math]
与等式[math]\displaystyle{ X=M_{-j}+2M_{-j}^2+3M_{-j}^3+\cdot\cdot\cdot }[/math]相减得到:
[math]\displaystyle{ XM_{-j}-X=-(M_{-j}+M_{-j}^2+M_{-j}^3+\cdot\cdot\cdot)=-M_{-j}U_{-j} }[/math]
于是,解出:
[math]\displaystyle{ X=M_{-j}U_{-j}^2 }[/math]
其中,[math]\displaystyle{ U_{-j}=\sum_{k=0}^{\infty}M_{-j}^k=(I-M_{-j})^{-1} }[/math] 所以,i到j的平均首达时间就是:
[math]\displaystyle{
l_{i,j}=\frac{\phi_{0i}(M_{-j}U_{-j}^2)_{ij}}{\phi_{i,j}}=\frac{\phi_{0i}(M_{-j}U_{-j}^2)_{ij}}{\frac{\phi_{0i}u_{ij}}{u_{jj}}}=\frac{u_{jj}(M_{-j}U_{-j}^2)_{ij}}{u_{ij}}
}[/math]
又根据马尔科夫链删除节点的性质,我们可以把上式简化为:
[math]\displaystyle{
l_{i,j}=\frac{u_{jj}(M_{-j}U_{-j}^2)_{ij}}{u_{ij}}=\frac{(MU^2)_{ij}}{u_{ij}}-\frac{(MU^2)_{jj}}{u_{jj}}
}[/math]
于是我们得到了从任意节点i到j的平均首达时间计算公式。将这个公式套用到图1所示的网络上,我们可以得到从任意点i到j的平均首达时间,这就构成了平均首达时间矩阵:
[math]\displaystyle{ L= \left( \begin{array}{ccccccc} 0 & 1 & 88/41 & 373/164 & 7218/2255 & 557/164 & 63/16 \\ \infty & 0 & 47/41 & 209/164 & 4963/2255 & 393/164 & 47/16 \\ \infty & \infty & 0 & 9/4 & 58/55 & 5/4 & 175/82 \\ \infty & \infty & 1 & 0 & 113/55 & 9/4 & 66/41 \\ \infty & \infty & 3 & 2 & 0 & 1 & 525/328 \\ \infty & \infty & 2 & 1 & 168/55 & 0 & 197/164 \\ \infty & \infty & \infty & \infty & \infty & \infty & 0 \end{array} \right) }[/math]
我们看到,这与前面计算的从0到所有点,以及从所有点到汇的距离是一致的,这进一步验证了这个方法的正确性。
平均时间
根据上述级数法求解平均首达时间的启发,我们还可以求出从任意点i到达任意点j的平均时间而非平均首达时间。这里,平均时间按照如下方式定义:所有经过i的节点染成红色,并且永不退色,而且,经过i的粒子就开启一个计时器,则从j点处统计红色粒子,计算它们计时器所经历的时间。
有趣的是,按照上述方法,这个平均时间比平均首达时间更容易计算。还是按照平均时间的定义:
[math]\displaystyle{ k_{i,j}=\sum_{k=1}^{\infty}kp^{k}_{i,j} }[/math]
这里[math]\displaystyle{ p^{k}_{i,j} }[/math]的计算不用再考虑首达问题,于是
[math]\displaystyle{ p^{k}_{i,j}=\frac{\phi_{0i}(M^k)_{i,j}}{T'_{i,j}} }[/math]
这里,[math]\displaystyle{ T'_{i,j} }[/math]应为从i到j的总流。理应代入前面得到的关于[math]\displaystyle{ T_{i,j} }[/math]的表达式。这大体上正确,只有在i=j的时候不正确。因为在[math]\displaystyle{ T_{i,i} }[/math]中包含了从0到i的首达流[math]\displaystyle{ \phi_{0,i} }[/math],而在平均时间的计算中,这部分流量不应包含,故而[math]\displaystyle{ T'_{i,i}=T_{i,i}-1 }[/math]。所以:
[math]\displaystyle{ T'_{i,j}=\phi_{0,i}(MU)_{ij} }[/math]
从而时间:
[math]\displaystyle{ p_{i,j}^k=\frac{(M^k)_{i,j}}{(MU)_{ij}} }[/math]
所以,平均时间的计算公式为:
[math]\displaystyle{
k_{i,j}=\frac{(MU^2)_{ij}}{(MU)_{ij}}
}[/math]
根据这个公式,计算图1所示网络,得到彼此平均时间的矩阵为:
[math]\displaystyle{ K= \left( \begin{array}{ccccccc} \infty & 1 & 365/164 & 193/82 & 529/164 & 285/82 & 63/16 \\ \infty & \infty & 201/164 & 111/82 & 365/164 & 203/82 & 47/16 \\ \infty & \infty & 273/82 & 191/82 & 177/164 & 109/82 & 175/82 \\ \infty & \infty & 177/164 & 273/82 & 341/164 & 191/82 & 66/41 \\ \infty & \infty & 505/164 & 341/164 & 669/164 & 177/164 & 525/328 \\ \infty & \infty & 341/164 & 177/164 & 505/164 & 273/82 & 197/164 \\ \infty & \infty & \infty & \infty & \infty & \infty & \infty \end{array} \right) }[/math]
有趣地是,对角线元素表达的是节点i到i的平均回归时间,它可以用于节点i的中心度刻画。
[math]\displaystyle{ k_{i,i}=(\infty,\infty,273/82,273/82,669/164,273/82,\infty) }[/math]
该数值越小,说明这个节点在整个网络中的流量循环也就越快。
另外,我们还可以通过比较平均时间矩阵和平均首达时间矩阵,会发现任意两点之间的平均时间都比平均首达时间要大一些,通过做这两个矩阵的差,我们得到:
[math]\displaystyle{ K-L= \left( \begin{array}{ccccccc} & 0 & 13/164 & 13/164 & 223/9020 & 13/164 & 0 \\ & & 13/164 & 13/164 & 223/9020 & 13/164 & 0 \\ & & 273/82 & 13/164 & 223/9020 &13/164 & 0 \\ & & 13/164 & 273/82 & 223/9020 &13/164 & 0 \\ & & 13/164 & 13/164 & 669/164 &13/164 & 0 \\ & & 13/164 & 13/164 & 223/9020 &273/82 & 0 \\ & & & & & & \end{array} \right) }[/math]
观察这个矩阵,我们发现,所有有值的列除了对角线拥有相同的数值。这表明任何一点到达某一个点的平均时间与首达平均时间之差均为常数,并且出于同一环上的不同节点具有相同的数值,例如2,3,5。
流距离算法
import numpy as np
import networkx as nx
# 计算流矩阵
def getFlowMatrix(G, nodelist=None):
if nodelist is None:
FM = nx.to_numpy_matrix(G)
FM = nx.to_numpy_matrix(G, nodelist)
return FM
# 使用函数:FlowMatrix = getFlowMatrix(G,nodelist)
# 计算M矩阵
def getMarkovMatrix(m):
n = len(m)
mm = np.zeros((n, n), np.float)
for i in range(n):
for j in range(n):
if m[i, j] > 0:
mm[i, j] = float(m[i, j]) / float((m[i, 0:].sum()))
return mm
# 使用函数:MarkovMatrix = getMarkovMatrix(FlowMatrix)
# 计算U矩阵
def getUMatrix(m):
I = np.eye(n)
mm = np.linalg.inv(I - m)
return mm
# 使用函数:UMatrix = getUMatrix(FlowMatrix)
# 计算L矩阵
def getLMatrix(m,u):
l = np.zeros((n,n))
mu_square = m.dot(u).dot(u)
for i in range(n):
for j in range(n):
l[i][j] = mu_square[i][j]/u[i][j] - mu_square[j][j]/u[j][j]
return l
#使用函数:getLMatrix(MarkovMatrix,UMatrix)
我们使用示例流网络的数据
G=nx.DiGraph()
G.add_edge('source',1,weight=80)
G.add_edge(1,2,weight=50)
G.add_edge(1,3,weight=30)
G.add_edge(3,2,weight=10)
G.add_edge(2,4,weight=20)
G.add_edge(2,5,weight=30)
G.add_edge(4,5,weight=10)
G.add_edge(5,3,weight=5)
G.add_edge(2,'sink',weight=10)
G.add_edge(4,'sink',weight=10)
G.add_edge(3,'sink',weight=25)
G.add_edge(5,'sink',weight=35)
nodelist = ['source',1,2,3,4,5,'sink']
n = G.number_of_nodes()
使用函数
FlowMatrix = getFlowMatrix(G,nodelist)
MarkovMatrix = getMarkovMatrix(FlowMatrix)
UMatrix = getUMatrix(MarkovMatrix)
LMatrix = getLMatrix(MarkovMatrix,UMatrix)
流网络根据流距离嵌入空间
- ↑ 引用错误:无效
<ref>标签;未给name属性为levine的引用提供文字