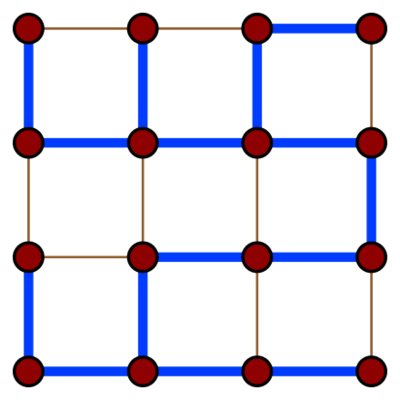
生成树
在数学领域的图论中,无向图G的生成树T是包含G的所有顶点且边数最少的连同子图。通常,一个图可能有许多的生成树,但是一个不连通的图不包含任何生成树。如果G的所有边都是G的生成树T的边,那么G是一个树并且和T完全相同(即该树有且仅有唯一的生成树并且就是它本身)。
应用
许多最短路径算法,比如Dijkstra的算法和A*搜索算法,内部都会构建一个生成树作为解决 问题的中间步骤。
为了最小化电力网络成本、无线网络连接、管道连接、自动语音识别等等,人们经常利用逐步建立生成树(或者多种树)的算法作为寻找最小生成树的中间步骤。
互联网和其他的通信网络都有传输链路,这些传输链路以网状拓扑结构将节点连接在一起,其中包括了一些循环。为了避免“桥环”和“路由环”,许多这类网络设计了路由协议,包括生成树路由协议、开放式最短路径路由协议、链路状态路由协议、增强树形路由协议等等,这要求每个路由器都要记住其生成树。
定义
树是没有循环的连通无向图。生成树是横跨图G(即包含G的每一个顶点),并且是G的一个子图(即每一个边都在树G中)。也可以把连通图G的生成树定义为不重复边的最大边集,或者定义为连接所有顶点的最小边集。
基本圈
只向生成树添加一条边就会创建一个新的圈,这样的圈称为基本圈。 不在生成树中的每条边都有一个独特的基本圈; 因此,在基本圈和不在生成树中的边之间存在一个双射。 对于具有 V 个点的连通图,任何生成树都有V-1条边,因此,E 条边的图及其生成树中的一条生成树都有 E-V+ 1个基本圈。 对于任意给定的生成树,所有 E-V+ 1基本圈的集合构成一个圈基,圈空间的基。
基本割集
与基本圈相对的概念是基本割集。 通过删除生成树的一条边,将顶点划分为两个不相交的集合。 基本割集定义为必须从图 G 中去除以完成相同分区的边的集合。 因此,每个生成树定义了一组 V-1基本割集,对于生成树的每条边都有一个基本割集。
基本割集和基本圈之间的对偶性是通过指出不在生成树中的圈边只能出现在圈的其他边的割集中来建立的; 反之亦然: 割集中的边只能出现在包含与割集对应的边的圈中。 这种对偶也可以用拟阵理论来表示,根据这种理论,生成树是图拟阵的基础,基本圈是在基础上加上一个元素而形成的集合内的唯一环路,基本割集也是由对偶拟阵以同样的方式定义的。
生成森林
在不连通的图中,不可能有生成树,则必须考虑生成森林。 有两种不同的定义:
- 一些研究者认为生成森林是给定图的最大非循环子图,或等效地由图的每个连接部分的生成树组成的图。
- 其他研究者则认为生成树是遍历所有顶点的森林,意味着图的每个顶点都是该森林中的一个顶点。对于此定义,即使连接图也可能具有断开连接的生成森林,例如其中每个顶点形成单个顶点树的森林。
为了避免这两种定义之间的混淆,Gross & Yellen (2005)建议对具有与给定图相同连通性的生成森林使用”完全生成森林”一词,而 Bondy & Murty (2008)则称这种森林为”最大生成森林”。
计算生成树
连通图的生成树的数量t(G)是一个经过充分研究的不变式。
在特定的图中
- 在某些情况下,直接计算t(G)很容易:
- 如果G本身是树,则t(G)=1。
- 当G是具有n个顶点的循环图Cn时,则t(G) = n。
- 对于具有n个顶点的完整图,Cayley公式给出了生成树的数量为[math]\displaystyle{ n^{n-2} }[/math]。
- 如果G是完整的而粪土[math]\displaystyle{ K_{p,q} }[/math],那么[math]\displaystyle{ t(G)=p^{q-1}q^{p-1} }[/math]
- 对于n维超立方体图[math]\displaystyle{ Q_n }[/math],生成树的数量是[math]\displaystyle{ t(G)=2^{2^n-n-1}\prod_{k=2}^n k^{{n\choose k}} }[/math]
在任意图中
通常,对于任何图 G,数t(G)可以在Polylogarithmic time内用用 Kirchhoff 矩阵树定理计算出来,作为从图中导出的矩阵的行列式。
具体来说,为了计算t(G),构造了一个方阵,其中的行和列都被G的顶点索引。 行 i 和列 j 中的条目是以下三个值之一:
- 顶点的度数i,如果i = j,
- -1,如果顶点i和j相邻,或者
- 如果顶点i和j彼此不同但不相邻,则为0 。
所得矩阵是奇异的,因此其行列式为零。但是,删除任意选择的顶点的行和列将导致行列式正好为t(G)的较小矩阵。
缺失-收缩
如果G是图或多重图,e是G的任意一边,则G的生成树的t (G)满足缺失-收缩递推t(G) = t(G − e) + t(G/e),其中G - e是删除 e 得到的多重图,G/e是G对e的收缩,公式中的项 t(G − e)计算G的不使用边 e 的生成树,项t(G/e) 使用e计算G的生成树。
在这个公式中,如果给定的图G是一个多重图,或者如果一个收缩导致两个顶点通过多条边连接在一起,那么冗余的边就不应该被去除,因为这会造成总数错误。 例如,一个键图由 k 条边连接两个顶点,它有 k 个不同的生成树,每个生成树由这些边中的一条组成。
Tutte多项式
图的 Tutte 多项式可以被定义为从图的“内部活动”和“外部活动”中计算出的项在图的生成树上的总和。 它在参数(1,1)处的值是生成树的数目,在不连通图中是极大生成森林的数目。
Tutte 多项式也可以用缺失-收缩递推来计算,但它的计算复杂度很高: 对于许多参数值,计算是#P-complete的,而且它也很难用近似比来近似。 用基尔霍夫定理求解的点(1,1)是为数不多可计算的例子。
算法
结构
一个图的单个生成树可以在线性时间内被深度优先搜索或广度优先搜索到。 这两种算法都探索给定的图,从一个任意的顶点v开始,通过循环遍历他们发现的顶点的邻居,并将每个未探索的邻居添加到一个数据结构中,以便以后探索。 它们的不同之处在于这种数据结构是堆栈(在深度优先搜索中是堆栈)还是队列(在广度优先搜索中是队列)。 在这两种情况下,都可以通过将除根顶点 v 以外的每个顶点连接到发现它的顶点来构成一个生成树。 根据用于构造这棵树的图形探索算法,这棵树被称为深度优先搜索或广度优先搜索。 深度优先搜索是一类生成树的特例,叫做Trémaux树。
生成树在并行和分布式计算中非常重要,它是维持一组处理器之间通信的一种方式; 例如, OSI 链路层设备使用的生成树协议协议或分布式计算的 Shout 协议。 然而,在连续计算机上构造生成树的深度优先和广度优先方法并不适用于并行计算机和分布式计算机。 相反,研究人员设计了几种更专门的算法,以便在这些计算模型中找到生成树。
优化
在图论的某些领域,找到一个加权图的最小生成树通常是有用的。生成树还有很多其他优化问题,包括最大生成树、跨度至少为 k 个顶点的最小生成树、每个顶点边数最少的生成树、叶数最多的生成树、叶数最少的生成树(与哈密顿路径问题树密切相关)、最小直径生成树和最小伸缩生成树。
最优生成树问题也研究了有限的点集在几何空间,如欧几里德平面。 对于这样的输入,生成树也是以给定点为顶点的树。 树的质量的衡量方式与图中相同,使用两对点之间的欧几里得度量作为每条边的权重。 因此,举例来说,一个欧几里得最小生成树就相当于一个具有欧几里德边权的完全图中的一个最小生成树。 然而,没有必要为了解决最佳化问题而构造这个图; 例如,欧几里得最小生成树问题可以在 o (n log n)时间内更有效地解决,方法是构造Delaunay三角,然后将线性时间平面图最小生成树算法应用于最终的三角剖分。
随机化
从所有生成树中以等概率随机选取的生成树称为一致生成树。 威尔逊算法通过在给定图上进行随机游动并消除游动产生的循环,可以在多项式时间内生成一致的生成树。
随机最小生成树是生成生成树的另一个随机但不一致的模型。 在这个模型中,给图的边赋予随机权,然后构造加权图的最小生成树。
在无限图中
每个有限连通图都有一个生成树。 然而,对于无限连通图,生成树的存在性等价于选择公理。 如果无限图的每一对顶点构成有限路的一对端点,则无限图是连通的。 和有限图一样,树也是没有有限圈的连通图,生成树可以定义为边的极大无圈集,也可以定义为包含每个顶点的树。
一个图中的树可以由它们的子图关系部分排序,并且这个部分排序中的任何无限链都有一个上界(链中树的并)。 Zorn 的引理是选择公理的众多等价命题之一,它要求所有链都是上界的偏序有一个极大元; 在图的树上的偏序中,这个极大元必是一个生成树。 因此,如果假设 Zorn 引理,则每个无限连通图都有一个生成树。
在另一个方向上,给定一个集族,可以构造一个无限图,使图的每一个生成树都对应于集族的一个选择函数。 因此,如果每个无限连通图都有一个生成树,那么选择公理就是正确的。
在有向图中
生成树的概念可以推广到有向多重图。给定有向多重图G上的一个顶点 v,以 v 为根的有向生成树 t 是G的一个非圈子图,其中除 v 以外的每个顶点都大于度1。 这个定义只有在 t 的“分支”指向 v 时才能满足。
参考
本中文词条由zq用户参与编译,欢迎在讨论页面留言。 本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。