算术表达式

算术表达式是由数和算术运算（也即四则运算）构成的表达式。算术表达式通常只是一个记录计算过程的符号串，它作为一个严密的数学对象本身的研究仍然是不充分的。对于一个复杂的数域，如实数域，记录一次计算过程本身写出一个表达式是容易的，然而作为一个概念，严格的定义实数域上的表达式仍然有内在的困难。这个困难之一来自于除零错误造成的语法与语义的不一致。另外一种困难来自于无限长度的表达式的计算，比如著名的令人迷惑的级数 [math]\displaystyle{ -\frac{1}{12}= 1 + 2 + 3 + ... }[/math]。

语法式定义

下面我们形式的引入有理数域上的算术表达式，因为此时我们可以存在算法判定如下的纯语法式构造什么时候会出现除零错误。

有理数域[math]\displaystyle{ \mathbb{Q} }[/math]上的算术表达式是指由如下产生式规则生成的符号串

[math]\displaystyle{ a \longleftarrow x }[/math]
[math]\displaystyle{ a \longleftarrow ( a + a ) }[/math]
[math]\displaystyle{ a \longleftarrow ( a - a ) }[/math]
[math]\displaystyle{ a \longleftarrow ( a \times a ) }[/math]
[math]\displaystyle{ a \longleftarrow ( a \div a ) }[/math]

其中 [math]\displaystyle{ x \in \mathbb{Q} }[/math]，我们称此时有 [math]\displaystyle{ a \in \mathbb{E} \left [\mathbb{Q} \right ] }[/math]。

字串与语法树表示

在上述生成过程中，我们可以得到一个算术表达式的字串表示或者树表示，两种表示是等价的。例如：

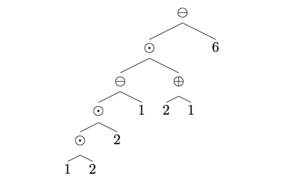
[math]\displaystyle{ (((((1 \times 2) \times 2) - 1) \times (2 + 1)) - 6)\label{eq:equation} }[/math]

相应的语法树如下：

严格地讲，如果我们把产生式的目标解读为字串，产生式规则对应字串拼接，我们就得到了字串表示；如果目标是一个树，产生式规则解读为两个子树拼接成一个更大的树，那么我们就得到了语法树表示。我们可以很容易的通过前序遍历从语法树表示得到字串表示。

由语法树表示，我们很容易的从子树引入子表达式的概念；树的内部节点对应操作符 +、−、×、÷ ，而叶节点对应数字。

表达式的估值

估值函数 [math]\displaystyle{ \nu }[/math] 是定义在算术表达式 [math]\displaystyle{ a \in \mathbb{E}[\mathbb{Q}] }[/math] 上的一个偏函数。仅当在递归求值过程中出现除以零的情况，估值过程才会变得没有定义。

我们可以递归地定义 [math]\displaystyle{ \nu(a) }[/math] 如下：

常数叶节点：对任意 [math]\displaystyle{ x \in \mathbb{Q} }[/math]，[math]\displaystyle{ \nu(x) = x }[/math]。
由 [math]\displaystyle{ + }[/math] 组成的分支：对于任意 [math]\displaystyle{ (a + b) }[/math]，[math]\displaystyle{ \nu((a + b)) = \nu(a) + \nu(b) }[/math]。
由 [math]\displaystyle{ - }[/math] 组成的分支：对于任意 [math]\displaystyle{ (a - b) }[/math]，[math]\displaystyle{ \nu((a - b)) = \nu(a) - \nu(b) }[/math]。
由 [math]\displaystyle{ \times }[/math] 组成的分支：对于任意 [math]\displaystyle{ (a \times b) }[/math]，[math]\displaystyle{ \nu((a \times b)) = \nu(a),\nu(b) }[/math]。
由 [math]\displaystyle{ \div }[/math] 组成的分支：对于任意 [math]\displaystyle{ (a \div b) }[/math]，如果 [math]\displaystyle{ \nu(b) \neq 0 }[/math]，则 [math]\displaystyle{ \nu((a \div b)) = \nu(a) / \nu(b) }[/math]。

我们称算术表达式 [math]\displaystyle{ a }[/math] 是可估值的（evaluable），如果 [math]\displaystyle{ \nu(a) }[/math] 有定义。除非另有说明，下文中我们只讨论可估值的算术表达式。

给定任意算术表达式 [math]\displaystyle{ a }[/math]（无论是否可估值），我们都可以得到它的树形表示。若一个节点 [math]\displaystyle{ l }[/math] 为叶节点，它对应的子表达式 [math]\displaystyle{ s }[/math] 是一个数字，因此我们将其视为已经“已估值”。若一个节点 [math]\displaystyle{ b }[/math] 为分支节点，对应的子表达式 [math]\displaystyle{ s }[/math] 是一个表达式，此时我们可以对它应用 [math]\displaystyle{ \nu }[/math] 得到一个数 [math]\displaystyle{ \nu(s) }[/math]。通过一个自底向上的递归估值过程，子表达式可以一个接一个地被估值，直到得到最终的表达式估值。

但是一般来讲，表达式的估值顺序通常并不唯一。

定义： 对一个算术表达式 [math]\displaystyle{ a }[/math] 的估值顺序，指的是对其树形表示中所有分支节点进行的一种排序方式，使得每个子节点（子表达式）都在其父节点之前被估值。

例如，对于上图中的算术表达式，其可能的估值顺序包括：

[math]\displaystyle{ 1 \times 2 \rightarrow \underline{2}; \underline{2} \times 2 \rightarrow \underline{4}; \underline{4} - 1 \rightarrow \underline{3}; 2 + 1 \rightarrow \underline{3}; \underline{3} \times \underline{3} \rightarrow \underline{9}; \underline{9} - 6 \rightarrow 3 }[/math]
[math]\displaystyle{ 1 \times 2 \rightarrow \underline{2}; \underline{2} \times 2 \rightarrow \underline{4}; 2 + 1 \rightarrow \underline{3}; \underline{4} - 1 \rightarrow \underline{3}; \underline{3} \times \underline{3} \rightarrow \underline{9}; \underline{9} - 6 \rightarrow 3 }[/math]
[math]\displaystyle{ 1 \times 2 \rightarrow \underline{2}; 2 + 1 \rightarrow \underline{3}; \underline{2} \times 2 \rightarrow \underline{4}; \underline{4} - 1 \rightarrow \underline{3}; \underline{3} \times \underline{3} \rightarrow \underline{9}; \underline{9} - 6 \rightarrow 3 }[/math]
[math]\displaystyle{ 2 + 1 \rightarrow \underline{3}; 1 \times 2 \rightarrow \underline{2}; \underline{2} \times 2 \rightarrow \underline{4}; \underline{4} - 1 \rightarrow \underline{3}; \underline{3} \times \underline{3} \rightarrow \underline{9}; \underline{9} - 6 \rightarrow 3 }[/math]

其中带有下划线的数字表示在估值过程中得到的中间结果。

实数域上的困难

实数域上的困难，主要是由 Richardson 定理带来的。我们不能轻易的断定两个由超越函数带来的实数在算术表达式组合下得到的值是不是零。不同于有理数域，可以存在整齐划一的算法来判定一个表达式是否为零。

另外一种困难是没有足够的计算资源去计算和分析一个大数是否满足一定的性质，比如我们不知道[math]\displaystyle{ e^{e^{e^{79}}} }[/math]是否是整数？由此，我们可以构造如下例的实数表达式

[math]\displaystyle{ \frac{1}{e^{e^{e^{79}}} - M} + 1 }[/math]

其中的 M 是所有比 [math]\displaystyle{ e^{e^{79}} }[/math] 小的质数的连乘积。我们可以构造出来许许多多这样的表达式，但它们的合法性很难或者无从讨论。

参考文献

本节的内容主要来自苑明理的研究手稿。