贝叶斯分类
贝叶斯决策理论
由乘法公式引出
P(AB) = P(B|A) P(A)
P(B|A) = P(AB) / P(A)
P(B|A) = P(A|B) P(B) / P(A)
对于指定对象从属于某一类别的问题从概率的角度可以理解为求P(B|A),意思是给定A的条件,求B发生的概率。那么对于多个类别集[math]\displaystyle{ W=\{w_1,w_2,...,w_n\} }[/math]和指定的随机变量[math]\displaystyle{ x }[/math],则有:
[math]\displaystyle{ W = \underset{w_i}{\operatorname{argmax}} P(w_i|x) }[/math]
求[math]\displaystyle{ x }[/math]出现在每一个[math]\displaystyle{ w_i }[/math]的概率。带入贝叶斯公式:
[math]\displaystyle{
P(w_i|x)=\frac{p(x|w_i)P(w_i)}{p(x)}
}[/math]
其中:
[math]\displaystyle{ P(w_i|x) }[/math] 后验概率,即所求结果。 [math]\displaystyle{ P(w_i) }[/math] 先验概率,可以通过训练样本直接求出。 [math]\displaystyle{ p(x|w_i) }[/math] 随机变量[math]\displaystyle{ x }[/math]的条件概率密度函数。 [math]\displaystyle{ p(x) }[/math] 随机变量[math]\displaystyle{ x }[/math]的概率密度函数,可通过全概率公式求出,但对于在给定的[math]\displaystyle{ x }[/math],不影响比较[math]\displaystyle{ P(w_i|x) }[/math]的结果,可以忽略不求。
从上式看出后验概率[math]\displaystyle{ P(w_i|x) }[/math]的求解取决于对x的条件概率密度函数[math]\displaystyle{ p(x|w_i) }[/math]的估计。
朴素贝叶斯
因为x的条件概率密度函数[math]\displaystyle{ p(x|w_i) }[/math]并不容易求得,也因如果在特定场合里,给定的样本集合是离散形式的数据,这样我们将求x的条件概率密度函数[math]\displaystyle{ p(x|w_i) }[/math]变为求解条件概率[math]\displaystyle{ P(x|w_i) }[/math]。
但求解有高维特征向量x的条件概率仍然很复杂。例如: n维向量的条件概率[math]\displaystyle{ P(x_1,x_2,...,x_n|w_i) }[/math]
[math]\displaystyle{ P(x_1,x_2,...,x_n|w_i) }[/math] [math]\displaystyle{ =P(x_1\vert w_i) \ P(x_2,\dots,x_n\vert w_i, x_1) }[/math] [math]\displaystyle{ =P(x_1\vert w_i) \ P(x_2\vert w_i, x_1) \ P(x_3,\dots,x_n\vert w_i, x_1, x_2) }[/math] [math]\displaystyle{ =P(x_1\vert w_i) \ P(x_2\vert w_i, x_1) \ P(x_3\vert w_i, x_1, x_2) \ P(x_4,\dots,x_n\vert w_i, x_1, x_2, x_3) }[/math] [math]\displaystyle{ =P(x_1\vert w_i) \ P(x_2\vert w_i, x_1) \ P(x_3\vert w_i, x_1, x_2) \ ,\dots, P(x_n\vert w_i, x_1, x_2, x_3,\dots,x_{n-1}). }[/math]
这样求解方法将随着n的增长使计算量直线上升,带来维数灾难的问题。
如果假设每个特征相互独立,那么将条件概率P(x|w_j)等于每个特征在类w_j下的条件概率P(x_i|w_j)的连乘
[math]\displaystyle{ P(x|w_i) = \prod_{j=1}^n P(x_j|w_i) }[/math]
因为事件独立性的前提假设,这样的数据环境其实服从伯努利分布,在通常情况下每个特征取值为二值,即[math]\displaystyle{ x_j \in \{0,1\} }[/math],即特征在一个样例中出现或者不出现。
最终朴素贝叶斯模型如下:
[math]\displaystyle{ P(w_i|x) \varpropto P(w_i) \prod_{j=1}^n P(x_j|w_i) }[/math] [math]\displaystyle{ W = \underset{w_i}{\operatorname{argmax}} \ P(W=w_i) \displaystyle\prod_{j=1}^n P(X_j=x_j\vert W=w_i) }[/math]
我们以上是依据事件独立性的假设来推出朴素贝叶斯模型,但也可以从高斯分布下的贝叶斯决策准则出发,通过最大后验概率估计(MAP)推导求出(下面再谈)。
朴素贝叶斯模型是生成模型,通过学习联合概率[math]\displaystyle{ P(x_j,w_i) }[/math]来求出分类结果。它因长相朴实,实现简单所以被广大群众喜闻乐见,但因独立性假设的前置条件,使得它在特征相互依赖的复杂的数据环境下并不适用。
高斯判别分析
高斯分布
在实践中,最常遇到的概率密度函数是高斯分布,如果不能判断现实数据环境的分布情况,也可以依据中心极限定理假设其概率密度函数近似服从高斯分布。
单变量高斯函数定义为:
[math]\displaystyle{
p(x)=\frac{1}{\sqrt{2 \pi}\sigma}exp(-\frac{(x-\mu)^2}{2\sigma^2})
}[/math]
其中,[math]\displaystyle{ \mu }[/math]为[math]\displaystyle{ x }[/math]均值,[math]\displaystyle{ \sigma^2 }[/math]为[math]\displaystyle{ x }[/math]的方差,表示[math]\displaystyle{ x }[/math]服从均值为[math]\displaystyle{ \mu }[/math]的方差为[math]\displaystyle{ \sigma^2 }[/math]的高斯分布,写为[math]\displaystyle{ p(x) \sim N(\mu, \sigma^2) }[/math]。服从高斯分布的样本聚集于均值附近,其散布程度与标准差[math]\displaystyle{ \sigma }[/math]有关。
在d维特征空间中,多元高斯函数定义为:
[math]\displaystyle{
p(x)=\frac{1}{(2 \pi)^{d/2} |\Sigma|^{1/2}}exp(-\frac{1}{2} (x-\mu)^T \Sigma^{-1}({x-\mu}))
}[/math]
其中:
[math]\displaystyle{ \mu }[/math] 为[math]\displaystyle{ x }[/math]d维均值向量 [math]\displaystyle{ \Sigma }[/math] 是d*d的协方差矩阵。定义为:[math]\displaystyle{ \Sigma=E[(x-\mu)(x-\mu)^T] }[/math]。 [math]\displaystyle{ |\Sigma| }[/math] 表示行列式的值 [math]\displaystyle{ \Sigma^{-1} }[/math] 表示矩阵的逆 [math]\displaystyle{ (x-\mu)^T }[/math] 是[math]\displaystyle{ (x-\mu) }[/math]的转置
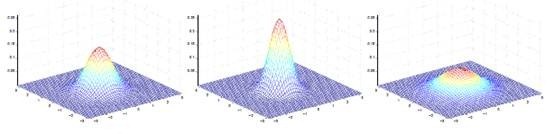
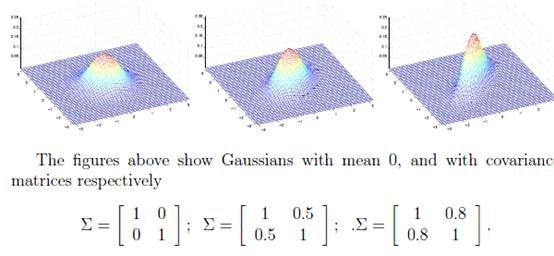
协方差矩阵的相关性
[math]\displaystyle{ \sigma_{ij} }[/math]是协方差矩阵[math]\displaystyle{ \Sigma }[/math]的第ij个元素,表示随机向量的任两个维度的相关度,那么:[math]\displaystyle{ \sigma_{ij} = E[(X_i - \mu_i)(X_j - \mu_j)] }[/math]
协方差矩阵有如下特性:
- 为了使[math]\displaystyle{ |\Sigma| }[/math]的值是一个正数,我们严格限定[math]\displaystyle{ \Sigma }[/math]是正定的。
- 协方差[math]\displaystyle{ \Sigma }[/math]是对称的,其主对角线上的元素是方差,其它为协方差。
[math]\displaystyle{ \sigma_{ij} \ge 0 }[/math] 表示第i列特征和第j列特征正相关 [math]\displaystyle{ \sigma_{ij} \le 0 }[/math] 表示第i列特征和第j列特征负相关 [math]\displaystyle{ \sigma_{ij} = 0 }[/math] 表示第i列特征和第j列特征不相关
- 其中均值决定中心位置(方位和高度),协方差决定决定投影椭圆的形状(朝向和大小)。
若方差[math]\displaystyle{ \sigma_{i}^2 \gt \sigma_{j}^2 }[/math],则椭圆投影向x_i轴拉伸,方差越小越陡峭 若协方差[math]\displaystyle{ \sigma_{ij} \gt 0 }[/math],则投影沿主对角线拉伸 若协方差[math]\displaystyle{ \sigma_{ij} \lt 0 }[/math],则投影沿副对角线拉伸
- 我们可以根据协方差矩阵计算任两个维度之间取值为(-1,1)之间的相关系数。
[math]\displaystyle{ corr(X_i, X_j)= \frac{\sigma_{ij}}{\sigma_i \sigma_j}, i,j=1,2,...,d }[/math]
[math]\displaystyle{ corr(x_i, x_j) = \frac{\sum_{t=1}^d (x_{it} - \overline{x_i}) (x_{jt} - \overline{x_j})}{\sqrt{\sum_{t=1}^d (x_{it} - \overline{x_i}) ^ 2} \sqrt{\sum_{t=1}^d (x_{jt} - \overline{x_j}) ^ 2}}, i,j=1,2,...,N }[/math]
多元高斯假设
从贝叶斯公式可以看出对条件概率密度函数[math]\displaystyle{ p(x|w_i) }[/math]的计算至关重要。在一些问题中,我们能够确定条件概率密度函数的类型,也就是得知他服从某一概率分布,那么问题就变成模型已知参数未知的估计问题。我们假设条件概率密度函数[math]\displaystyle{ p(x|w) }[/math]服从高斯分布,则有
[math]\displaystyle{ p(w)=\phi^{w}(1-\phi)^{1-w} }[/math] [math]\displaystyle{ p(x|w=i)=p(x;\mu_i,\Sigma)=\frac{1}{(2 \pi)^{d/2} |\Sigma|^{1/2}}exp(-\frac{1}{2} (x-\mu_i)^T \Sigma^{-1}({x-\mu_i})) }[/math]
最大似然估计如下:
[math]\displaystyle{ l(\phi,\mu_i,\Sigma)=log\prod_{j=1}^m p(x^{(j)},w^{(j)};\phi,\mu_i,\Sigma) }[/math] [math]\displaystyle{ l(\phi,\mu_i,\Sigma)=log\prod_{j=1}^m p(x^{(j)}|w^{(j)};\mu_i,\Sigma)p(w^{(j)};\phi) }[/math]
最大似然估计的解法是根据待估参数对似然函数求偏导,再使偏导等于0后求极致得到参数的式子,在高斯分布中,最大似然估计出来的参数等价于样本的均值和方差,这里略去证明,直接得到结果为:
[math]\displaystyle{ \phi=\frac{1}{m}\sum_{j=1}^{m}L\{w^{(j)}=i\} }[/math] [math]\displaystyle{ \mu_i=\frac{\sum_{j=1}^mL\{w^{(j)}=i\}x^{(j)}}{\sum_m^{j=1}L\{w^{(j)}=i\}} }[/math] [math]\displaystyle{ \Sigma=\frac{1}{m}\sum_{j=1}^m(x^{(j)}-\mu_{w(j)})(x^{(j)}-\mu_{w(j)})^T }[/math]
判别分析
如果我们将P(Y|X)=P(X|Y)P(Y)使用判别函数g_i(x)获得:
[math]\displaystyle{ g_i(x)=-\frac{1}{2}(x-\mu_i)^T\Sigma_i^{-1}(x-\mu_i)-\frac{d}{2}ln2\pi-\frac{1}{2}ln|\Sigma_i|+lnP(w_i)+w_{i0} }[/math]
我们分情况讨论这个式子以简化函数
情况1:特征独立假设[math]\displaystyle{ \Sigma_i=\sigma^2I }[/math]
如果有样本数据的各特征统计独立,并且每个特征具有显通的方差[math]\displaystyle{ \sigma^2 }[/math]时,在这样的情况下协方差矩阵仅仅是[math]\displaystyle{ \sigma^2 }[/math]与单位矩阵I的乘积,为对角矩阵。几何上,它的样本数据落于同等大小的超椭球体,这样上式中的[math]\displaystyle{ |\Sigma_i| }[/math]与[math]\displaystyle{ (d/2)ln2\pi }[/math]对于任意g_i(x)都相等,可以省略。因此我们可以得到
[math]\displaystyle{ g_i(x)=-\frac{||x-\mu_i||^2}{2\sigma^2}+lnP(w_i) }[/math]
其中[math]\displaystyle{ ||x-\mu_i||^2 }[/math]是欧几里德范数,展开就是关于x的二次函数,但实际上关于i的协方差矩阵相等,所以没必要计算,使它变成了可省略计算的常量,于是,我们得到线型判别函数:
[math]\displaystyle{ g_i(x)=w_i^Tx+w_{i0} }[/math] [math]\displaystyle{ w_i=\frac{1}{\sigma^2}\mu_i }[/math] [math]\displaystyle{ w_{i0}=\frac{-1}{2\sigma^2}\mu_i^T\mu_i+lnP(w_i) }[/math]
情况2:同方差假设[math]\displaystyle{ \Sigma_i=\Sigma }[/math]
当所有类的协方差矩阵均相当,各自均值向量任意,几何上,样本落在相同大小和相同形状的超椭球体聚类中,第i类的聚类中心在向量[math]\displaystyle{ \mu_i }[/math]附近,式中的[math]\displaystyle{ |\Sigma_i| }[/math]与[math]\displaystyle{ (d/2)ln2\pi }[/math]对于任意g_i(x)都相等,可以省略。
[math]\displaystyle{ g_i(x)=-\frac{1}{2}(x-\mu_i)^T\Sigma^{-1}(x-\mu_i)+lnP(w_i) }[/math]
与情况1同方差假设不同的是,样本数据各个统计特征不独立,图形投影不是正圆,点到判决函数的距离由欧式距离退化到马式距离(Mahalanobis)[math]\displaystyle{ d_m=[(x-\mu_i)^T\Sigma^-1(x-\mu_i)]^{1/2} }[/math]
[math]\displaystyle{ g_i(x)=w_i^Tx+w_{i0} }[/math] [math]\displaystyle{ w_i=\Sigma^{-1}\mu_i }[/math] [math]\displaystyle{ w_{i0}=-\frac{1}{2}\mu_i^T\Sigma^{-1}\mu_i+lnP(w_i) }[/math]
情况3:高斯假设[math]\displaystyle{ \Sigma_i= }[/math]任意
一般的多元高斯分布,每一类的协方差矩阵是不同的,唯一可以去掉的一项是[math]\displaystyle{ (d/2)ln2\pi }[/math],其判别函数显然是二次型。在两类问题中,对应的判定面是超二次曲面,可以是超平面,超平面对,超球体,超椭球体,超抛物面,超双曲面等各种二次曲面。
[math]\displaystyle{ g_i(x)=X^TW_ix+w_i^Tx+lnP(w_i) }[/math] [math]\displaystyle{ W_i=-\frac{1}{2}\Sigma_i^{-1} }[/math] [math]\displaystyle{ w_i=\Sigma_i^{-1}\mu_i }[/math] [math]\displaystyle{ w_{i0}=-\frac{1}{2}\mu_i^T\Sigma^{-1}\mu_i-\frac{1}{2}|\Sigma_i|+lnP(w_i) }[/math]